面向装配定位的大视场测量系统组合标定方法
王宝俊 张 超 崔海华 姜 涛 傅世强 王鸿熠 吴 凯
2021年中国航天大会专栏
面向装配定位的大视场测量系统组合标定方法
王宝俊张 超崔海华姜 涛傅世强王鸿熠吴 凯
(1. 南京航空航天大学智能材料与结构航空科技部级重点实验室,南京 210016;2.北京航星机器制造有限公司,北京 100013)
针对航天大部件装配中的定位过程,为解决所使用的视觉系统标定方法复杂、标定精度低的问题,提出一种平面靶标和一维靶标组合的双目视觉系统标定方法。该方法结合单应性变换原理,利用小型平面靶标进行组合标定视觉系统内参,将内参作为输入,利用一维编码靶标标定视觉系统外参,在保证内外参数标定精度的基础上,大大简化双目视觉系统实际使用过程中的标定步骤,能够有效提高标定效率。实际标定实验结果表明,双目视觉系统标定精度可达0.08mm,获得相机内参后可对外参进行在线标定,标定精度和效率均较高。
双目视觉系统标定;平面靶标;一维编码靶标;单应性变换;归一化算法
1 引言
在航天大部件装配过程中由于部件尺寸大、刚性弱、易变形等特性,对其定位引导精度提出了较高要求。视觉方式作为常见的测量检测、定位引导和精度验证的手段,因其精度高、操作简便而广泛应用。视觉系统在使用中,标定是最为基础和关键的技术之一,标定的方法和结果影响着最终的效率和精度。视觉系统标定是指建立图像像素位置与场景点位置之间的关系,途径是根据相机模型由特征点的图像坐标和世界坐标求解相机内外参数。
双目视觉系统作为常见的视觉测量方式,国内外学者已经对其标定方法做了大量研究工作。按照是否使用标定物,标定方法可分为主动视觉标定方法和使用标定物的标定方法。主动视觉标定方法需要控制相机按照特定方式移动,难以保证相机运动精度,因此在实际应用中难以推广。使用标定物的标定方法按照标定物的不同又可以分为三维靶标法、平面靶标法和一维靶标法。三维靶标法标定精度高,但其存在自遮挡问题,且制造加工难度大,实际应用较为困难;平面靶标法标定精度较高,但问题在于靶标要覆盖整个视场才能保证标定精度,故靶标尺寸大、标定步骤复杂;一维靶标法标定精度略低于前两种方法,但其标定方式灵活高效且成本低,适合在线标定。
针对航天大部件装配定位的实际环境与条件,单一的标定方法难以同时满足高精度高效率的要求。本文提出一种平面靶标和一维靶标组合的双目视觉系统标定方法,利用小型平面靶标组合构造覆盖相机整个视场的大型平面靶标,进而标定双目系统内参,以内参作为输入,利用一维编码靶标在线标定外参。实验表明,该方法在保证双目视觉系统标定精度的基础上,能够有效简化标定步骤,提高标定效率。
2 双目视觉系统模型

图1 双目视觉模型示意图



左右相机坐标系之间的相互位置关系可通过空间转换矩阵表示为:


实际相机成像过程中会存在畸变,一般只考虑径向和切向畸变。径向畸变可描述为:

切向畸变可描述为:


3 组合式标定原理
3.1 基于组合式平面靶标的内参标定
在利用平面靶标进行相机内参标定时,要想获得高精度的标定结果,靶标的尺寸需要和测量视场范围一样大,而大尺寸的平面靶标设计制造困难。因此采用将多个小型平面靶标组合构造大型靶标的方式进行标定,在保证内参标定精度的同时,小型平面靶标制造相对简单,且成本较低。

图2 平面靶标组合示意图









式(9)可改写为:


上述步骤未考虑镜头畸变,同时标定图像会存在一定噪声,因此需要进一步采用列文伯格-马夸尔特算法(Levenberg-Marquardt,LM算法)优化相机内参。
设双目视觉系统共拍摄了张标定图像,为标定过程中使用的小型平面靶标数目,分别建立左右相机最优化目标函数:



至此,通过小型平面靶标组合的方式已得到最优的左右相机内部参数。由于相机内部参数只与相机本身特性有关,故认为外界环境改变不会影响相机内参。标定好内部参数后,认为相机内参在很长一段时间内不会改变。在双目系统实际使用中,只需进行一次上述相机内参标定,后续使用时只要对双目系统左右相机外部参数进行在线标定即可,因此可以简化实际使用时的标定步骤。
3.2 基于一维靶标的外参标定
已有很多学者研究利用一维靶标对双目系统进行标定,其中最关键的步骤是如何通过多组匹配图像点坐标快速准确地解算相机外参初值。对于这一问题,最经典的方法是基于对极几何原理的八点算法。
3.2.1 传统八点算法解算基础矩阵




因此,式(13)可化为与本质矩阵有关的方程。


基础矩阵和本质矩阵都是双目视觉系统的关键参数,二者类似。由式(13)或式(15),只要知道多组匹配像点坐标即可解算。一般采用8对匹配像点进行基础矩阵或本质矩阵的求解,即传统的八点算法。
3.2.2 加权平移归一化算法解算基础矩阵
传统八点算法是易于实现的线性算法,但其对噪声数据异常敏感,并且求得的解不稳定,估计得到的基础矩阵精度也不高,原因在于八点法在处理时认为每对匹配点对阵的影响都是相同的,但实际上每个点误差不同,对阵的影响也各不相同。因此,采用一种加权平移归一化算法,引入余差作为权因子,以排除噪声干扰,使得高精度的匹配点对阵的影响大而低精度的匹配点影响小。
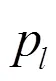

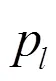


式中:是向量Fp的第个分量。
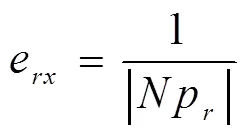






再对图像坐标作归一化处理:




3.2.3 解算外部参数

奇异值分解得到的只是比例意义上的,还需对其结合一维靶标长度进行绝对定向。通过一维靶标已知的真实长度和测量所得特征点间比例意义上的距离求解比例系数,进而最终确定平移向量。
3.2.4 非线性优化外部参数
在相机外参标定过程中由于图像噪声的影响会导致最终标定结果的不准确,因此结合一维靶标特征点距离约束对相机外参进行LM非线性优化,建立最优化目标函数



4 标定实验与结果分析
本文提出的算法均已使用C++编程语言完成实现。为验证所提出的双目系统平面靶标和一维靶标组合式标定方法的可行性和有效性,对双目视觉系统进行了标定实验。
标定实验环境和条件如下:双目视觉系统两相机采用德国映美精CMOS工业相机,型号为DMK 33GP031,相机分辨率为2592×1944pixel(5MP),镜头焦距为8mm,测量距离约为2m。
对于标定内参所用的小型平面靶标,采用如图4a所示的形式。小型平面靶标正中间的方形编码标志边长为75mm,其作用是确定靶标坐标系,同时不同的编码标志可以区分不同的小型靶标,以便于组合。靶标上各圆点的半径为15mm,圆心间距为45mm。将4个小型平面靶标进行组合以覆盖双目视觉系统整个视场范围,如图4b所示。

图4 小型平面靶标示意图
按照这种组合方式在相机视场内调整靶标,获得不同的位姿关系,左右相机分别拍摄20张图像,然后利用本文标定方法标定双目系统内参矩阵,内参标定结果如表1所示。

表1 双目视觉系统内参标定结果
为验证内参标定精度,对平面靶标上的特征点进行三维重建,统计左右相机20张图像每张图像重建出的靶标特征点坐标之间的距离的平均值,并与真值45mm进行比较,比较结果如图5所示。

图5 靶标特征点距离重建结果
由图5可以看出,靶标特征点重建精度基本保持在±0.1mm以内,可见精度较高。
标定外参所用的一维靶标采用如图6的形式,一维靶标上粘贴有编码标志点。相较于传统圆形标志点,编码点具有匹配性好、提取精度高、不需要特定匹配算法等优点。

图6 一维靶标示意图
将一维靶标在双目视觉系统视场内任意摆放20次,获得左右相机拍摄图像,利用本文方法标定外参,并与传统的八点算法进行比较,标定和比较的结果如表2所示。

表2 双目视觉系统外参标定结果

图7 两种方法余差结果比较
为验证外参标定精度,采用余差作为衡量标准之一,确保减少噪声对图像坐标点的干扰,保证本文算法的正确性。本文方法与传统八点算法在余差上的差异如图7所示。
由图7可以看出,两种方法余差曲线图趋势一致,因此可以说明本文方法的正确性。同时由余差数据可以明显看出,本文所计算的余差精度是传统八点算法的100倍左右。
再将矩阵的条件数作为衡量标准,判断估计的基础矩阵的鲁棒性好坏。矩阵的条件数是对矩阵误差或不确定度的敏感性的度量,直接反映了矩阵的鲁棒性,条件数越大,矩阵的鲁棒性就越差,这时矩阵称做是病态的;条件数越小,矩阵的鲁棒性就越好,这时矩阵称做是良态的。矩阵的条件数和范数有关,表3显示了不同范数下本文算法和传统八点算法所估计的基础矩阵的差异。
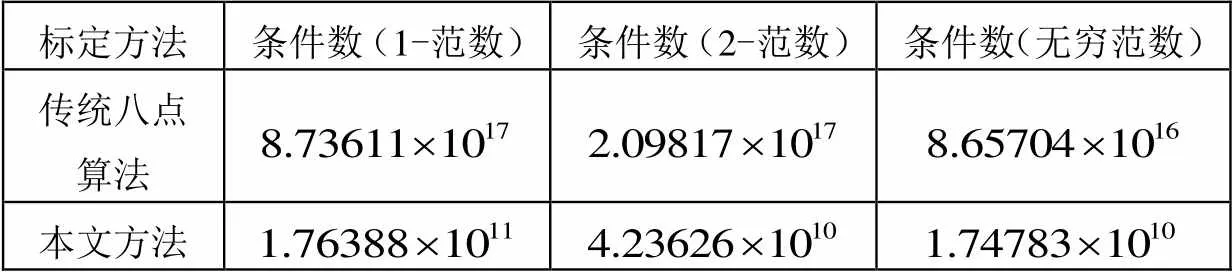
表3 两种方法基础矩阵条件数比较
从表3可以看出,在不同的范数下,传统八点算法所估计出的基础矩阵条件数是本文方法的10~10倍,因此本文方法可以有效改善基础矩阵的条件数,提高了基础矩阵的鲁棒性。
因此综合余差和矩阵的条件数两种衡量标准,本文的外参标定方法可以有效提高基础矩阵估计的精度,提高外参结果的精度。
最后,本文利用标定好的双目视觉系统观测小型标准靶标,进一步验证本文标定方法的准确性和有效性。如图8所示,每个小型标准靶标两点之间的距离均为90mm,通过标定好的双目视觉系统进行测量和三维重建。

图8 小型标准靶标示意图
将测量结果与标准值进行比对,测量结果如图9所示。
由图9分析可知,测量结果最大误差为0.179mm,最小误差为0.011mm,误差平均值为0.078mm,测量结果的均方根误差为=0.081mm。将本文方法与其他文献或方法进行对比,对比结果如表4所示。

图9 小型标准靶标测量结果
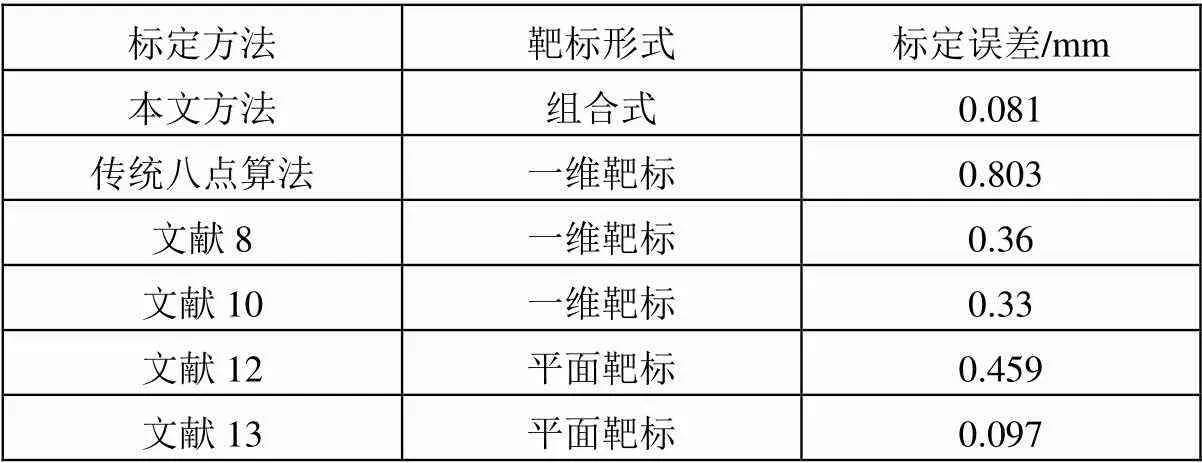
表4 不同标定方法结果对比
由表4分析可知,本文的组合式标定方法测量误差均低于其他文献中的方法,因此说明本文标定方法可以获得较高的标定精度。
4 结束语
在航天大部件的装配定位过程中,视觉系统的标定是最为基础和关键的技术之一。本文提出一种平面靶标和一维靶标组合的双目视觉系统标定方法,利用小型平面靶标进行组合构造覆盖相机整个视场的大型平面靶标,进而标定双目系统内参,利用一维编码靶标结合加权平移归一化算法标定外参。实验结果表明,本文方法能够在保证双目视觉系统标定精度的基础上,有效简化标定步骤,提升视觉系统的标定效率,可行性与实用性较高。
1 张广军. 视觉测量[M]. 北京:科学出版社,2008:102~103
2 朱嘉,李醒飞,徐颖欣. 摄像机的一种主动视觉标定方法[J]. 光学学报,2010,30(5):1297~1303
3 孙军华,刘震,张广军,等. 基于柔性立体靶标的摄像机标定[J]. 光学学报,2009,29(12):3433~3439
4 王晨,张宗华,丁宇航,等. 基于立体标靶的双目系统标定研究[J]. 光学技术,2020,46(3):322~329
5 Zhang Zhengyou. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22 (11): 1330~1334
6 Valsamis N, Ilias K, George K, et al. Fully automatic camera calibration using regular planar patterns[J]. Int Arch Photogram Remote Sens Spatial Inf Sci, 2008, 37(B5): 21~26
7 王亮,吴福朝. 基于一维标定物的多摄像机标定[J]. 自动化学报,2007,33 (3):225~231
8 杨珍,孙军华,吴子彦,等. 基于双一维靶标的摄像机标定方法[J]. 光电子·激光,2010,21(3):411~414
9 Amini K, Rostami F. A modified two steps Levenberg-Marquardt method for nonlinear equations[J]. Journal of Computational and Applied Mathematics, 2015, 288: 341~350
10 Zhang Zhengyou. Camera calibration with one-dimensional objects.[J]. IEEE transactions on pattern analysis and machine intelligence, 2004, 26(7):892~899
11 周富强,张广军,魏振忠,等. 基于未知运动一维靶标的双目视觉传感器标定[J]. 机械工程学报,2006,42(6):92~96
12 杨景豪,刘巍,刘阳,等. 双目立体视觉测量系统的标定[J]. 光学精密工程,2016,24(2):300~308
13 倪章松,顾艺,柳庆林,等. 大视场双目立体视觉柔性标定[J]. 光学精密工程,2017,25(7):1882~1889
Combined Calibration Method of Large Field of View Measurement System for Assembly Positioning
Wang BaojunZhang ChaoCui HaihuaJiang TaoFu ShiqiangWang HongyiWu Kai
(1. Ministry Level Key Laboratory of Aeronautical Science and Technology for Intelligent Materials and Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016;2. Beijing Hangxing Machinery Manufacturing Co., Ltd., Beijing 100013)
A binocular vision system calibration method based on the combination of plane target and one-dimensional target is proposed in this paper for the problems of complex calibration method and low calibration accuracy in the positioning process of aerospace large parts assembly.This method combines the small plane target to calibrate internal parameters of vision system, based on the homography transform principle and taking the internal parameters as the input data, uses one-dimensional coding target to calibrate external parameters of vision system. On the basis of ensuring the calibration accuracy of internal and external parameters, it greatly simplifies the calibration steps in the actual use of binocular vision system, and can effectively improve the calibration efficiency.The experimental results show that the calibration accuracy of the binocular vision system can reach 0.08mm. After obtaining the internal parameters of the camera, the external parameters can be calibrated online, thus the calibration accuracy and efficiency are both high.
calibration of binocular vision system;plane target;one dimensional coded target;homography transformation;normalization algorithm
O439
A
国家重点研发计划2019YFB2006100、2019YFB17075001;江苏高校优势学科建设工程资助项目;南京航空航天大学研究生创新基地(实验室)开放基金项目kfjj20200108。
王宝俊(1997),硕士,仪器科学与技术专业;研究方向:双目视觉、三维测量。
2021-04-08


