基于优化极限学习机的人造板厚度在线检测

张晴 朱良宽 Alaa M.E. Mohamed 史晗

摘 要：为提高人造板厚度检测精度，提出一种基于改进哈里斯鹰优化 （Harris Hawk Optimization， HHO） 算法提升极限学习机（ Extreme Learning Machine，ELM）的人造板厚度检测方法。通过对HHO算法进行改进，并利用优化后的算法对ELM的权值和偏置值等参数进行选择，在提升算法性能的基础上保留其寻优机制。同时，在初始种群位置中引入Tent映射反向学习，减少了不必要的全局搜索，在不影响种群多样性的条件下提高算法的收敛速度。最后以中密度纤维板（Medium Density Fiberboard，MDF）为例进行在线检测实验，得到实验数据并进行对比分析。实验结果显示，所提方法能够有效地减少测量误差，提高测量精度，具有一定的实际应用价值。

关键词：中密度纤维板;极限学习机;哈里斯鹰优化算法;Tent映射;反向学习策略;在线测厚系统

中图分类号：TS653.6;TP183    文献标识码：A   文章编号：1006-8023（2021）04-0058-08

Online Detection of Wood-based Panel Thickness via Optimized

Extreme Learning Machine

ZHANG Qing1， ZHU Liangkuan1*， MOHAMED Alaa M.E.1，2， SHI Han1

（1.College of Mechanical and Electrical Engineering， Northeast Forestry University， Harbin 150040， China;

2.Department of Mechanical and Electrical Engineering， Alzaim Alazhary University， Khartoum 1432， Sudan）

Abstract：In order to improve the accuracy of wood-based panel thickness detection， a wood-based panel thickness detection method based on improved Harris Hawk Optimization （HHO） algorithm and Extreme Learning Machine （ELM） was proposed. By improving the HHO algorithm， and using the optimized algorithm to select parameters such as weight and bias values of extreme learning machine， the optimization mechanism was retained on the basis of improving the performance of the algorithm. At the same time， reverse learning of tent mapping was introduced into the initial population position to reduce unnecessary global search and improve the convergence speed of the algorithm without affecting the population diversity. Finally， taking Medium Density Fiberboard （MDF） as an example， the on-line detection experiment was carried out， and the experimental data were obtained and compared. The experimental results showed that the proposed method can effectively reduce the measurement error and improve the measurement accuracy， which had a certain practical application value.

Keywords：Medium density fiberboard; Extreme Learning Machine; Harris Hawk Optimization algorithm; Tent map; reverse learning strategy; thickness online detection system

收稿日期：2021-03-25

基金項目：中央高校基本科研业务非专项资金项目（2572018BF02）;948资助项目（2014-4-46）;国家自然科学基金项目（31370565）;黑龙江省博士后启动基金项目（LBH-Q13007）

第一作者简介：张晴，硕士研究生。研究方向为智能控制、集群优化算法研究。E-mail： zhangqing686666@163.com

*通信作者：朱良宽，博士，教授，博士生导师。研究方向为林业工程自动化及智能化。E-mail： zhulk@126.com

引文格式：张晴，朱良宽， Alaa M.E. Mohamed，等. 基于优化极限学习机的人造板厚度在线检测[J].森林工程，2021，37（4）：58-65.

ZHANG Q， ZHU L K， MOHAMED A M E， et al. Online detection of wood-based panel thickness via optimized extreme learning machine[J]. Forest Engineering，2021，37（4）：58-65.

0 引言

人造板具有环保、尺寸稳定性好和质地均匀等优点，已逐渐成为家具制造和建筑业中最常用的材料之一。我国所生产和制造的人造板产品总量占全球人造板生产和制造总量的50%～60%。我国在人造板及其制品的生产制造、应用方面是世界第一大国，同时也是出口世界的第一大国，人造板已经成为我国不可替代的经济支柱产业之一[1-3]。

在人造板的工业生产中，人造板厚度是一个重要的生产指标，会直接影响到人造板生产的整体质量水平，而人造板厚度的预测在热压过程中起着十分重要的作用。因此，提高人造板厚度在线测量的准確性能够提高生产效率，减低生产资源损耗[4]。在人造板的生产环境中，由于内部和外部环境的整体影响，以及复杂的机械振动会导致动态误差[5]，这是常规测量仪器无法做到的，并且满足不了生产要求。在工程实践中，由于人造板在热压和外部环境的干扰下，再结合复杂的内部环境和外部因素，如设备振动在线检测过程中因为受到噪声的影响会降低测量的准确性，很难满足工业发展的需要，所以达不到所预期的测量效果，导致了人造板质量的下降。

近年来，智能的建模方法大量应用在厚度测量中。传统的神经网络模型虽然可以用于数据拟合中，通过不断的训练减小误差，但是在这个过程中，常需要大量数据去训练模型，无法保证模型精度[6-7]。相对于传统的神经网络，极限学习机（Extreme Learning Machine，ELM）网络结构简单，节省了大量的学习时间，能够解决传统神经网络学习速度慢、耗费时间长，且模型不精确的问题[8-10]。尽管ELM优点众多，但是应用到不同的领域具有不同的情况，ELM很难凭借自身优秀的性能找到最优的参数、最优的网络结构，尤其是参数选取不当，使得网络学习性能和查询样本的预测能力差，会导致对复杂和不规则数据预测的准确性和稳定性降低，从而不能满足实际要求。目前对于参数的选取常采用人工选取的方式，这十分耗费人力物力和时间资源，并且选择的参数也不一定准确，从而会导致整个预测模型的精度下降，性能降低。通过研究得出结论，利用不同的智能优化算法对ELM的参数进行优化，会使得ELM模型精确度更高[11-12]。因此，部分学者利用群智能优化算法对ELM的参数进行选取和优化。Wang等[13]提出利用灰狼优化算法优化ELM的模型，有效地提高了该模型的分类精度。Lv等[14]提出改进的细菌觅食优化算法应用于ELM参数的选取，且在躯体化障碍患者的诊断方面取得了成功的应用。Heidari等[15]提出了一种通过观察哈里斯鹰得到的一种全新思想的群智能算法并命名为哈里斯鹰优化（Harris Hawk Optimization，HHO）算法，此算法不仅全局搜索能力很强，而且需要调节的参数很少。但是，HHO有着与其他群智能优化算法一样的缺陷，包括收敛速度慢、容易陷入局部最优。Hussain等[16]提出将长期记忆引入HHO算法，使个体参考过去的经验进行运动，加强了种群多样性。Jia等[17]采用动态控制参数的方法改善了HHO算法容易陷入局部最优的情况，并通过变异算子进一步提高全局搜索的效率;Qu等[18]引入信息交换机制对HHO进行优化，增强了种群的多样性;Zhang等[19]引入指数递减策略更新能量因子的方法对HHO进行优化，有效地提高了算法的性能。

综上，本文将HHO算法应用于人造板厚度在线检测，提出一种改进的HHO的人造板厚度在线检测算法，通过对初始种群进行改进，改善了原算法的寻优精度。使用不同厚度规格的中密度纤维板（Medium Density Fiberboard，MDF）作为测试样本进行检测，并比较各种模型下的误差大小，分析所提方法的可行性及有效性。

1 极限学习机（ELM）

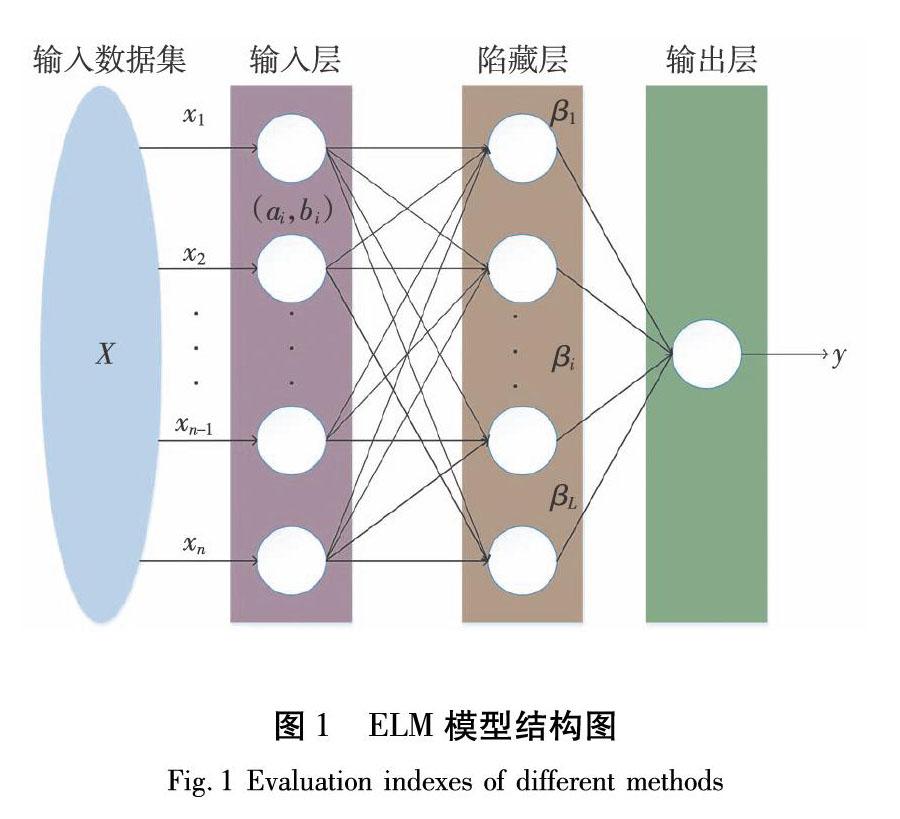
ELM为了达到精确学习的目的，利用增加隐藏层节点的个数的方法，隐藏层节点个数的确定通常需要参考样本数，一般规定样本的数目就是最大的隐藏层节点个数，因此无须通过迭代即可达到精确非线性拟合的效果。模型的基本结构如图1所示。

设W为ELM模型中输入层与隐藏层间的连接权值矩阵，形式为：

W=w11w12…w1n

w21w22…w2n

…………

wl1wl2…wlnl×n。（1）

设β为隐藏层与输出层间的连接权值矩阵，形式为：

β=β11β12…β1m

β21β22…β2m

…………

βl1βl2…βlm

l×m。（2）

式中：wij为隐藏层第i个神经元与输入层第j个神经元xj的连接权值;βik为隐藏层第i个神经元与输出层第k个神经元的连接权值。

设阈值向量b为：

b=[b1，b2，…，bl]T。（3）

则由ELM得到的输出神经元y的拟合统一表达式为：

y=∑li=1βigwix+bi。  （4）

式中g（x）为网络激励函数。一般选择：

g（x）=11+e-x。（5）

为了计算仿真模型的输出函数，对训练样本进行训练。设输入矩阵X含有q个训练集样本，矩阵X为 ：

X=x11x12…x1q

x21x22…x2q

…………

xn1xn2…xnq

n×q。（6）

设输出矩阵Y含有q个训练集样本，矩阵Y为 ：

Y=Y11Y12…Y1q

Y21Y22…Y2q

…………

Ym1Ym2…Ymq

m×q

。（7）

设wi为单隐藏层中第i个神经元与输入层神经元的连接权值向量，即：

wi=[wi1，wi2，…，win]。 （8）

设xp为第p个训练样本的输入层神经元向量，即：

xp=[x1p，x2p，…，xnp]T。  （9）

设激励函数为：

g（x）=11+e-x。 （10）

对于一个有l个隐藏层节点的神经结构模型，H假设为ELM的单隐藏层输出矩阵，自变量与权值的内积，则ELM神经元的输出矩阵H可以表示为：

H=g∑nj=1wjxj+b。  （11）

设该样本训练集的输出神经元函数为t，则将所有输出函数排成矩阵构成网络输出矩阵T，T的结构简单表示为：

T=[t1，t2，…，tq]。 （12）

tp=t1pt2p…tmp=∑li=1βi1gwixp+bi∑li=1βi2gwixp+bi…∑li=1βimgwixp+bi。（13）

利用最小二乘法解方程組：

minβ||Hβ-T′||。 （14）

依据 MP 广义逆理论，则该方程组的解表示为：

Hβ=T′。（15）

式中T′表示输出矩阵T的转置矩阵。

2 HHO算法

在迭代搜索过程中，鹰和猎物分别代表着空间的任意一个解和最优解，解随着位置的不断迭代更新，猎物的位置表示问题的理论最优解[20]。初始化时，鹰可能停落在搜索空间[lb，ub]的任意位置随时等待着猎物出现并抓捕猎物，lb为搜索空间下界，ub为搜索空间上界，在搜索过程中，根据其他个体和猎物的位置，以p的概率有选择地对其进行更新。

X（t+1）=Xd（t）-r1|Xd（t）-2rx2X（t）|，p≥0.5

（Xt（t）-Xm（t））-r3（lb+r4（ub-lb）），p<0.5 。（16）

式中：X（t+1）和X（t）分别为第t+1次和第t次迭代时哈里斯鹰的位置;Xt和Xd分别为猎物和鹰个体任意停留的位置;ri（i=1，…，4）和p都是在[0，1]范围内的一个任意数值;

Xm=∑Ni=1Xi（t）/N为所有鹰个体在第t次迭代时停落的平均位置。

猎物的能量即猎物逃脱被鹰捉捕的概率，能量高则易逃脱，其能量定义为：

E=2E0（1-tT）。 （17）

式中：T为最大迭代次数;E0为（-1，1）内的能量初始值。

当|E|≥0.5时鹰将在整个空间进行搜索，表示猎物在整个解空间中逸出;当|E|<0.5时，哈里斯鹰则搜索部分空间。

HHO利用因子β的范围来表示猎物是否逃脱鹰的抓捕，β的范围通常在[0，1]之间，以0.5为能量分界线，当β<0.5时表示猎物没有被鹰抓捕，胜利逃脱了;当β≥0.5时，表示猎物成功被鹰抓获。同时，鹰将猎物能量E和0.5进行比较来决定采取何种捕猎方法，其中包括4种情形。

情形1：软围捕。当β≥0.5 且|E|≥0.5时，表示猎物的能量E很高，并且随时进行逃脱尝试，结果总是失败并被抓获，所以鹰的位置更新公式为：

X（t+1）=ΔX（t）-E|JXt（t）-X（t）|。（18）

式中：ΔX（t）=Xt（t）-X（t）为第t次迭代时鹰与猎物的距离差;J=2（1-r5）为猎物逃跑时的力量强度，其中，r5∈（0，1）为此范围内的任意数值。

情形2：硬围捕。当β≥0.5且|E|<0.5时，表示鹰的位置较新，猎物的能量E较低导致了猎物直接被鹰捕获，其位置表达为：

X（t+1）=Xt（t）-E|ΔX（t）|。（19）

情形3：累速俯冲式软围捕。当β<0.5且|E|≥0.5时，表示猎物能量E很高将会成功逃脱，但鹰继续以充沛的力量抓捕猎物，位置更新为：

X（t+1）=Y∶Xt（t）-E|JXt（t）-X（t）|，iff（Y）f（X（t））

Z∶Y+S×LF（D），iff（Z）f（X（t））。（20）

式中：D为维度;S为D维随机行向量;LF为Levy函数;表示目标值达到更优的效果。

情形4：累速俯冲式硬围捕。当β<0.5且|E|<0.5时，表示猎物能量E较低，而鹰穷追猛赶猎物，缩小了鹰与猎物的距离，位置更新为：

X（t+1）=Y∶Xt（t）-E|JXt（t）-Xm（t）|，iff（Y）f（X（t））

Z∶Y+S×LF（D），iff（Z）f（X（t））。（21）

HHO算法以能量E来决定搜索方式，利用因子β表示鹰与猎物之间的4种狩猎情况，使问题得到最优的解决方案[21]。

3 改进HHO算法（IHHO）

3.1 改进的初始种群

标准HHO算法基于随机性产生初始种群，这可能会导致初始种群分布不均，不能保证种群的多样性。混沌是一种复杂的非线性系统动态行为，混沌优化利用混沌运动的特点来提高算法的寻优效率，基本思想即把优化变量通过混沌映射线性地映射到混沌变量中，再根据混沌的遍历性、随机性进行优化搜索，最后将得到的解线性地转化到优化变量空间。现有的混沌映射主要有Tent映射、Logistic映射等，Logistic映射混沌序列分布不均匀，寻优较慢，搜索效率较低;Tent映射混沌序列分布均匀，寻优较快，搜索效率较高，因此本文选用Tent映射[22]。反向学习策略目前广泛地应用于各种算法改进中，主要思想是同时考虑当前解及其相反解，能够有效地提高随机搜索算法的搜索能力。

初始种群的分布对算法的性能有着很大的影响，丰富的初始种群将会帮助提高优化算法的性能[23-24]。为了增强种群的多样性，提高算法的全局搜索能力与求解效率，采用Tent映射对哈里斯鹰群进行初始化，并使用反向学习策略优化初始种群[25-28]，将反向学习的Tent混沌初始化方法和HHO算法相结合的方法来确定初始解，从选择的初始种群中随机选择一个个体来代替初始解，即可得到改进的初始种群。

Tent映射的数学表达式为：

xn+1=2xn，0≤xn≤12   2（1-xn），12≤xn≤1。 （22）

反向解定义为：在D维空间中的一个可行解为x=（x1，x2，…，xD），x=[a，b]，则其反向解为

x′=（x′1，x′2，…，x′D），其中x′i=a+b-xi.。

综上，基于Tent 映射和反向学习策略的总体种群初始化步骤如下。

步骤1：使用Tent映射在搜索空间中搜索定位N个哈里斯鹰的位置xij（i=1，2，…，D;j=1，2，…，N）作为初始种群OB。

步骤2：根据反向学习相关原理，每个哈里斯鹰xij产生初始种群OB，每个哈里斯鹰xij的反向群体xij′作为反向种群FB。

步骤3：将2个种群OB和FB合起来，并选择适应度值排序达到前N名的哈里斯鹰个体作为初始种群。

3.2 适应度函数计算公式

fit=ei。（23）

式中：ei为N个体对应的 ELM 输入层权值和隐藏层阈值训练时的误差平方和。ei的计算公式为：

ei=∑Ni=1（yi-yi^）2。 （24）

式中：yi^为真实的输出值;yi为期望的输出值;N为样本数。

3.3 改进哈里斯鹰优化算法实现步骤

步骤1：种群初始化。根据搜索空间的上下边界范围，利用Tent映射和反向学习策略初始化每个个体。

步骤2：计算初始适应度。利用公式（24）计算所有个体的适应度值，将比较后适应度值最大的个体位置作为猎物的位置。

步骤3：位置更新。先通过公式（22）更新猎物的能量，然后根据能量和生成的随机数执行搜索或开发行为中对应位置更新策略。

步骤4：计算适应度。通过公式（24）计算位置更新后的每个个体的适应度，并将这些适应度值与猎物的适应度值进行比较，适应度较大的值作为更新后的猎物的适应度值。

将步骤3和步骤4进行循环往复的计算操作，当算法迭代的次数达到设定的最大迭代次数时，目标位置就是当前输出猎物的位置。

3.4 改进HHO优化ELM

将IHHO（改进后的HHO）算法用于优化ELM输入权重和隐藏层阈值，以达到提高网络性能和模型预测精度的目的。算法流程如图2所示。

4 实验分析

4.1 实验设备

本文所设计的检测装置主要包括由光栅位移传感器构成的测量头、CT架、异步电机、传动辊台、光电传感器、空气压缩器、控制柜、键盘和显示器所组成的测量系统，如图3所示。测量需要的所有組件均安装在垂直且彼此独立的CT机架中，跨过测量所需的传输设备。

4.2 模型构建

（1）IHHO优化算法参数设置

本次实验设置IHHO优化算法种群数量为30，迭代次数为500，搜索空间上下界为-1和1。

（2）ELM神经网络参数设置

在ELM网络中，包含7个输入节点和1个输出节点，输入层的7个节点分别为：A、B、C、D、E 5个测量通道的测量值、真值和速度，输出节点为预测值，传递函数使用Sigmoid函数，ELM的初始权重和偏差是通过随机方式获得的。为避免在确定隐藏层节点数时出现“欠拟合”和“过拟合”问题，在预测模型中使用“试错法”作为参考，得到隐藏层节点个数为15，每种厚度训练次数为70，测试次数为30，精度目标为0.001。

4.3 性能评估

为评估本文所提算法的检测性能，选用以下3个指标来对模型的优化性能进行评估。各评估指标的计算公式如下。

（1）均方根误差（ Root Mean Square Error， RMSE，公式中用RMSE表示）

RMSE=1n∑ni=1（yi-yi^）2。  （25）

（2）平均绝对百分比误差（Mean Absolute Percent Error， MAPE，公式中用MAPE表示）：

MAPE=1n∑ni=1|yi-yi^yi|。  （26）

（3）平均绝对误差（ Mean Absolute Error， MAE，公式中用MAE表示）：

MAE=1n∑ni=1|yi-yi^|。  （27）

式中：n为样本点数量;yi和yi^分别为人造板厚度数据真实值和预测值。

图4为迭代过程中HHO-ELM算法和IHHO-ELM算法的收敛曲线。由图4可以明显看出：IHHO-ELM模型的适应度值在模型收敛的迭代次数在200附近时达到稳定，可以得出改进的HHO能够为最快的收敛速度内找到问题的最优解，帮助ELM获得最佳参数，优化后收敛速度明显上升。

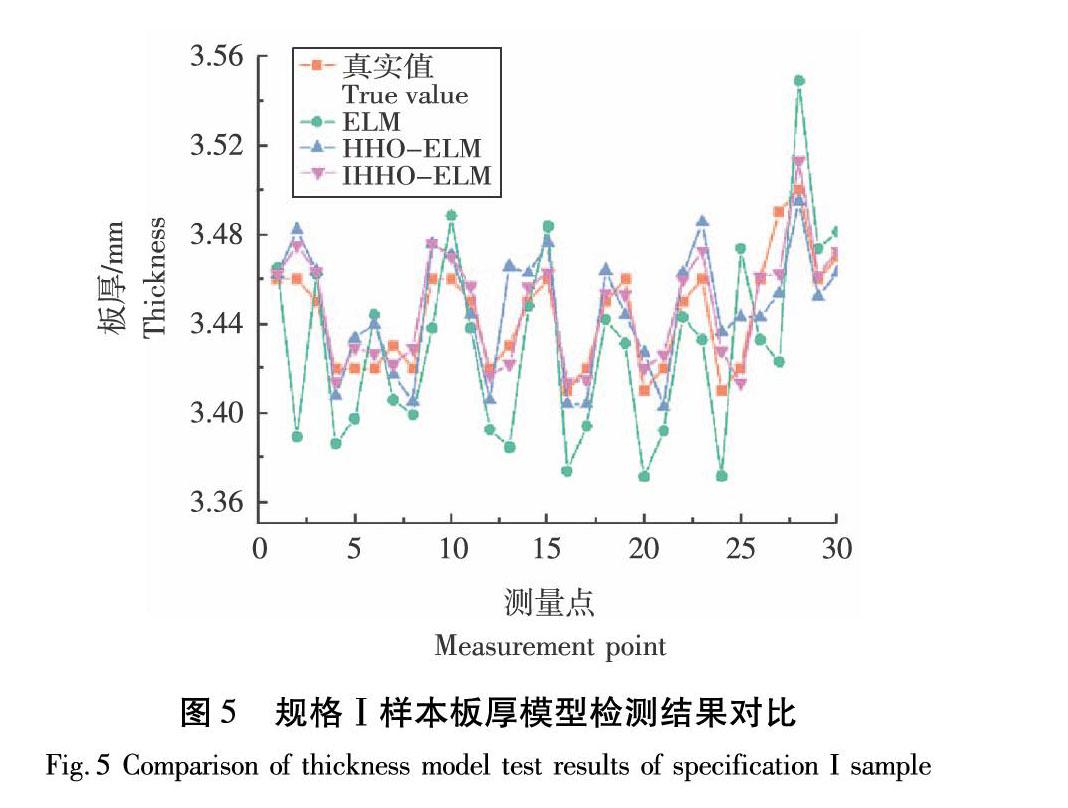
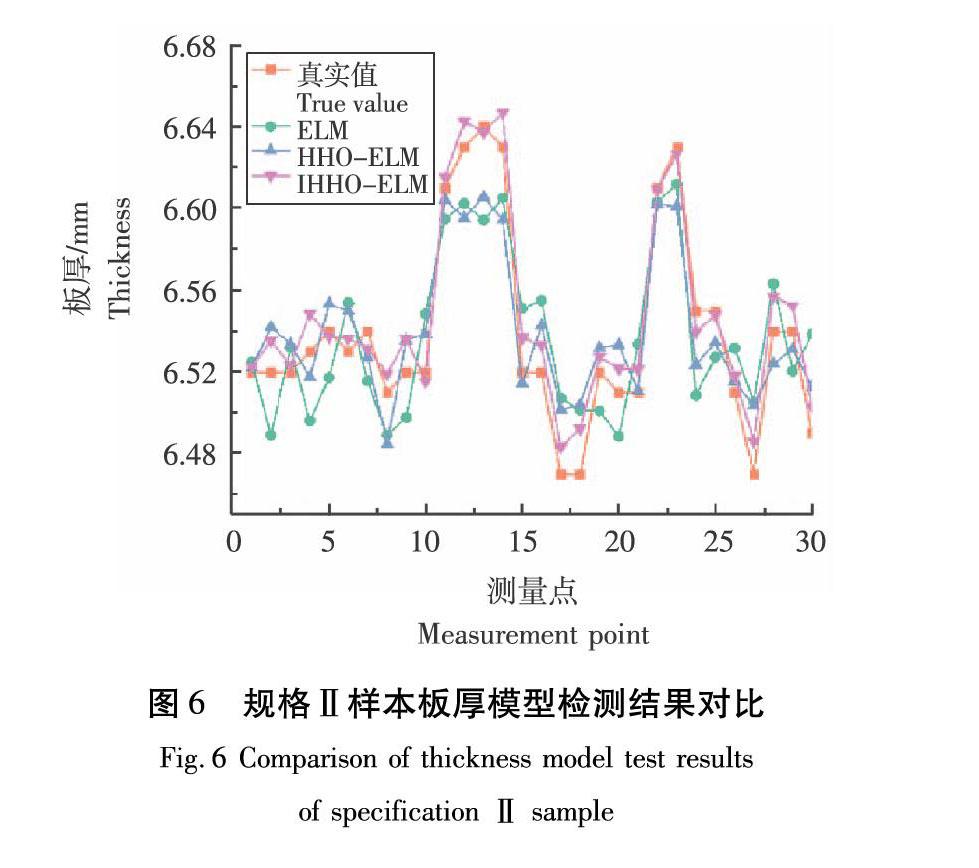
在本文中，测量真值由千分尺实际测量获取，预测值定义为基于误差补偿后的检测值。以A通道为例，选取3种不同规格的MDF测试样本进行厚度检测试验，得到不同模型（原始ELM预测模型、原始HHO-ELM优化预测模型及改进IHHO-ELM预测模型）的检测结果，如图5—图7所示。通过对比可以看到：IHHO-ELM拟合曲线明显优于其他2种模型拟合效果。进一步由不同模型的误差指标分析对比，可以明显看到，IHHO-ELM模型的检测误差最小，精度由高到低排序为：IHHO-ELM、 HHO-ELM 、ELM。

圖8为利用3种模型对于测量人造板厚度的绝对误差结果。从图8可以看出，IHHO-ELM模型的误差补偿方法可以有效地减少MDF厚度检测误差，提高检测精度。

为进一步分析IHHO-ELM、HHO-ELM和ELM模型的预测性能，利用公式（25）—公式（27）计算了3种模型的性能指标，见表1。经计算得出：

IHHO-ELM预测模型的均方根误差比ELM模型下降了68.88%;

IHHO-ELM预测模型的平均绝对百分比误差比ELM模型下降了69.81%;IHHO-ELM预测模型的平均绝对误差比ELM模型下降了57.24%。结果表明本文所提出的模型具有较为理想的检测精度。

5 结束语

在ELM相关理论的基础上，提出一种改进的HHO优化算法——IHHO，利用此算法优化了传统的ELM模型，并将此模型应用于人造板厚度在线检测。通过设计不同规格板厚的实际对比试验，ELM、HHO-ELM与IHHO-ELM对人造板厚度测量都有误差补偿的效果，相比之下，IHHO-ELM模型的补偿效果更明显，所提出的方法在收敛速度和检测精度方面均有良好的表现。

【参 考 文 献】

[1]QIN G Y， CHENG B D， ZENG Y C. Analysis of the impact of Chinese wood product manufacturers exports[J]. Forest Products Journal， 2015， 65（7/8）： 387-394.

[2]朱嘉智，朱猛，温明宇， 等. 阻燃无甲醛胶黏剂制备胶合板的研究[J]. 森林工程， 2020， 36（6）： 58-64.

ZHU J Z， ZHU M， WEN M Y， et al. Research on plywood by flame retardant and aldehyde free adhesive[J]. Forest Engineering， 2020， 36（6）： 58-64.

[3]WU X Z， NIU H， LI X J， et al. A study on the GA-BP neural network model for surface roughness of basswood-veneered medium-density fiberboard[J]. Holzforschung， 2020， 74（10）：248.

[4]朱良宽， 王沛煜， 王子博， 等. 带有高增益观测器的MDF连续热压系统滑模控制[J]. 森林工程， 2017， 33（5）： 79-84.

ZHU L K， WANG P Y， WANG Z B， et al. Sliding mode control for MDF continuous hot-press system with high gain observer[J]. Forest Engineering， 2017， 33（5）： 79-84.

[5]XIAO C J， ZHANG J C， ZHENG L J， et al. Error suppression of glass online laser thickness measurement using complementation of transmission and reflection[J]. Acta Photonica Sinica， 2017， 46（2）：212001.

[6]ZHONGH， H， MIAO C， C， SHEN Z， Z， et al. Comparing the learning effectiveness of BP， ELM， I-ELM， and SVM for corporate credit ratings[J]. Neurocomputing， 2014， 128： 285-295.

[7]WANG H， LIU D， ZHANG J， et al. Log-periodic power law hybrid model based on BP neural network[J]. Evolutionary Intelligence， 2021（3）： 1-9.

[8]ZHENG G Z， HUA W H， QIU Z H， et al. Detecting water depth from remotely sensed imagery based on ELM and GA-ELM[J]. Journal of the Indian Society of Remote Sensing， 2020， 49： 947-957.

[9]HUANG G B， ZHOUH， DING X， et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems， Man， and Cybernetics， Part B （Cybernetics）， 2012， 42（2）： 513-529.

[10]TIAN Z， LI S， WANG Y， et al. Network traffic prediction method based on improved ABC algorithm optimized EM-ELM[J]. The Journal of China Universities of Posts and Telecommunications， 2018， 25（3）： 37-48.

[11]LI S， HE H， LI J. Big data driven lithium-ion battery modeling method based on SDAE-ELM algorithm and data pre-processing technology[J]. Applied Energy， 2019， 242： 1259-1273.

[12]ZHANG Z， ZHANG A， SUN C， et al. Research on air traffic flow forecast based on ELM non-iterative algorithm[J]. Mobile Networks and Applications， 2021， 26（2）： 1-15.

[13]WANG M L ， CHEN H L ， LI H Z， et al. Grey wolf optimization evolving kernel extreme learning machine： Application to bankruptcy prediction[J]. Engineering Applications of Artificial Intelligence， 2017， 63：54-58.

[14]LV X N， CHEN H L， QIAN Z， et al. An improved bacterial-foraging optimization-based machine learning framework for predicting the severity of somatization disorder[J]. Algorithms， 2018， 11（2）： 17.

[15]HEIDARI A A， MIRJALILI S， FARIS H， et al. Harris hawks optimization： algorithm and applications[J]. Future Generation Computer Systems， 2019， 97：849-872.

[16]HUSSAIN K， ZHU W， SALLEH M N M. Long-term memory Harris hawk optimization for high dimensional and optimal power flow problems[J]. IEEE Access， 2019， 10：147596-147616.

[17]JIA H M， PENG X X， KANG L F， et al. Pulse coupled neural network based on Harris hawks optimization algorithm for image segmentation[J]. Multimedia Tools and Applications， 2020， 79：28369-28392.

[18]QU C W， HE W， PENG X N， et al. Harris hawks optimization with information exchange[J]. Applied Mathematical Modelling. 2020，84：52-75.

[19]ZHANG Y， ZHOU X， SHIH P C. Modified Harris hawks optimization algorithm for global optimization problems[J]. Arabian Journal for Science and Engineering， 2020， 45：10949-10974.

[20]GUPTA S， DEEP K， HEIDARI A A， et al. Opposition-based learning Harris hawks optimization with advanced transition rules： principles and analysis[J]. Expert Systems with Applications， 2020， 158：113510.

[21]KENANOGLU R， BALTACIOGLU M K， DEMIR M H， et al. Performance & emission analysis of HHO enriched dual-fuelled diesel engine with artificial neural network prediction approaches[J]. International Journal of Hydrogen Energy， 2020， 45（49）：26357-36369.

[22]LIU B， LIU J， CHEN F， et al. A video encryption algorithm based on integer dynamic coupling tent mapping[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics， 2020， 24（3）： 335-345.

[23]NASKAR P K， BHATTACHARYYA S， NANDY D， et al. A robust image encryption scheme using chaotic tent map and cellular automata[J]. Nonlinear Dynamics， 2020， 100（3）：2877-2898.

[24]PICHARDO-MENDEZ J L， PALACIOS-LUENGAS L， MARTINEZ-GONZALEZ R F， et al. LSB pseudorandom algorithm for image steganography using skew tent map[J]. Arabian Journal for Science and Engineering， 2020， 45（4）：3055-3074.

[25]ALAWAD N A， ABED-ALGUNI B. Discrete island-based cuckoo search with highly disruptive polynomial mutation and opposition-based learning strategy for scheduling of workflow applications in cloud environments[J]. Arabian Journal for Science and Engineering， 2021， 46（4）： 3213-3233.

[26]GUO Z L， SHI J X， XIONG X F， et al. Chaotic artificial bee colony with elite opposition-based learning[J]. International Journal of Computational Science and Engineering， 2019， 18（4）： 383.

[27]CHEN Y X， CHEN Z C， WU L J， et al. Parameter extraction of PV models using an enhanced shuffled complex evolution algorithm improved by opposition-based learning[J]. Energy Procedia， 2019， 158： 991-997.

[28]EWEES A A， ELAZIZ M A， HOUSSEIN E H. Improved grasshopper optimization algorithm using opposition-based learning[J]. Expert Systems with Applications， 2018， 112：156-172.