一种开放式风冷机箱内部器件温度评估方法*

刘冠宏

（中国电子科技集团公司第二十研究所，陕西西安 710068）

引 言

随着电子技术的快速发展，设备的功率密度越来越大，散热不良导致的热失效成为电子设备失效的主要形式。据统计，超过60%的电子设备失效问题是由散热问题引起的[1-2]。因此，能够解决电子设备过热问题的热分析、热设计和热测试技术得到了迅速发展[3]。

在电子设备的设计阶段就需要通过复杂的仿真计算来获得模块内部发热器件的温度，进而估测电子设备能否满足规定的环境条件。由于模块化和综合化的迅猛发展，多厂家的协同研发越来越普遍。系统级的热分析往往需要收集各个厂家的数模和热源分布情况才能进行。这样，不合理的设计使整个系统的分析和设计过程多次重复，进而消耗大量的时间和精力。因此非常有必要寻找一种既能估算系统内器件的温度又可降解系统指标的相对简单的方法来指导设计。

对于多维稳态导热问题，往往要通过有限元法建立复杂的连续性方程，再通过寻找边界条件求解，但该方法适用于软件仿真而不适合人力计算。

杨晨光、杨爱波等分别对硅基微槽和矩形肋片的热阻抗进行了研究，通过热阻抗来分析、优化散热结构的散热性能[4-5]。张华玲等建立了低气压条件下某被服系统的系统热阻计算模型，进而对系统的总热阻进行了计算和研究[6]。于翰文等对某双驱动进给系统进行了热阻网络等效，从而获得了其温度场分布模型，最终计算出了滚球丝杠的轴向热误差[7]。等效热阻网络可以应用于电子设备的机箱设计，一些研制任务书里也对某些通用件的热阻值及接触热阻值进行了规定。

本文以开放式风冷机箱为例，提出了一种等效热阻模型的计算方法，将机箱的传热计算分解成了求解系统各个传热环节热阻的问题，使热分析变得简单且可分解。

1 开放式风冷机箱结构简介

1.1 开放式风冷机箱结构组成

本文选用的算例为一个车载开放式风冷机箱模型，其结构形式为一个标准的7U（1U=44.45 mm）插箱，外形如图1所示。

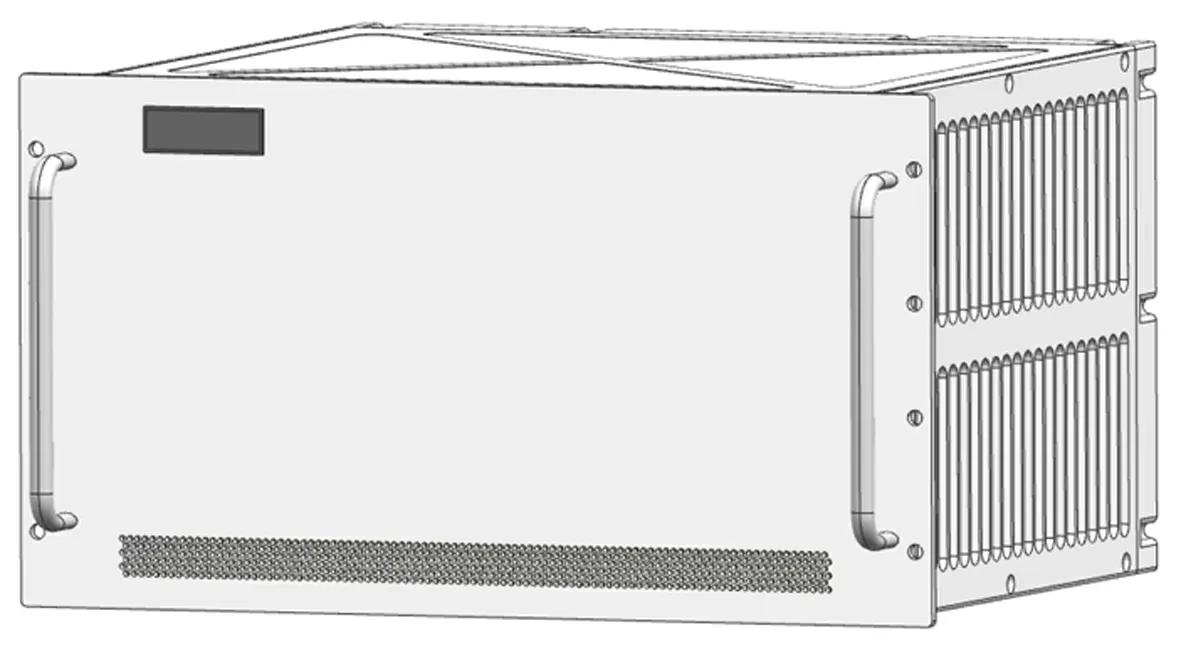
图1 开放式风冷机箱外形图

该机箱由上下导轨、上下盖板、2块侧板、母板、前后盖板及内插模块组成，如图2所示。机箱内部的框架上按模块高度要求安装导轨，导轨在模块插拔时起导向的作用。模板背板从后面固定在机箱上。各功能模块（现场可更换模块）可沿机箱中的导轨推入，通过锁紧机构锁定。锁紧机构采用滑块锁紧形式，能够满足机箱的冲击、振动要求。插拔机构在模块插入和拔出时提供足够的插入和分离力，保证模块与母板之间的连接器稳定地插入和分离。导轨、侧板、盖板及母板围起来形成上下风道。2台风机安装在机箱的后盖板上。

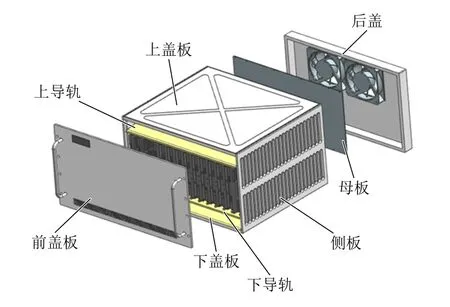
图2 开放式风冷机箱组成图

该机箱内插12个基于ASAAC标准的现场可更换模块（Line Replaceable Module, LRM）。LRM模块的组成如图3所示。

图3 LRM模块组成图

盒体由铝合金铣加工而成。印制板固定在盒体内部，为了满足散热要求，安装在印制板上的发热器件顶部通过导热脂与散热盖板紧贴在一起。连接器用于连接母板，传递数据，在结构上起定位的作用。侧面通过螺钉连接散热盖板，散热盖板上的散热齿增大了换热面积，起到了优化散热效果的作用。盒体上下两侧安装楔形锁紧条，后立面安装插拔机构，二者将模块固定、锁紧在机箱内。

1.2 风道设计

机箱内的上下导轨设计了通风口，如图4所示。该设计起到了引流的作用。机箱后盖上风扇的工作方式为抽风。空气从设备前面板下部的通风口进入设备，通过下导轨的通风口沿着模块的间隙向上，通过上导轨的通风口，最后被风扇抽离机箱。

图4 开放式风冷机箱导轨示意图

整个机箱的风道为“Z”字形风道，其设计如图5所示。由图5可知：由机箱的上盖板、上导轨和2个侧板组成的空间为上风道；由机箱的下盖板、下导轨、2个侧板及母板组成的空间为下风道；2个模块之间的间隙和导轨的通风口构成了模块间的风道。

图5 开放式风冷机箱风道示意图

模块内部发热器件紧贴散热盖板的背面，其热量一部分传导至散热盖板的散热齿面，与模块间风道的空气换热，一部分传导至模块上下表面的导轨上，与上下风道的空气对流换热，还有一部分传导至与模块散热盖板相对的盒体底面，与模块间风道的空气换热。此外，模块的散热面和盒体底面与邻近模块的盒体底面和散热面之间还存在辐射换热。

2 开放式风冷机箱热阻计算

2.1 等效热阻网络

由于强迫对流散热带走了绝大部分热量，辐射散热比重较小，且模块表面平整度较高，黑度较低，对温度变化的影响较小，因此本文在等效模型时暂不考虑辐射散热。

根据上一节描述的传热路径，模块内部发热器件产生热量后的热流示意图如图6所示。

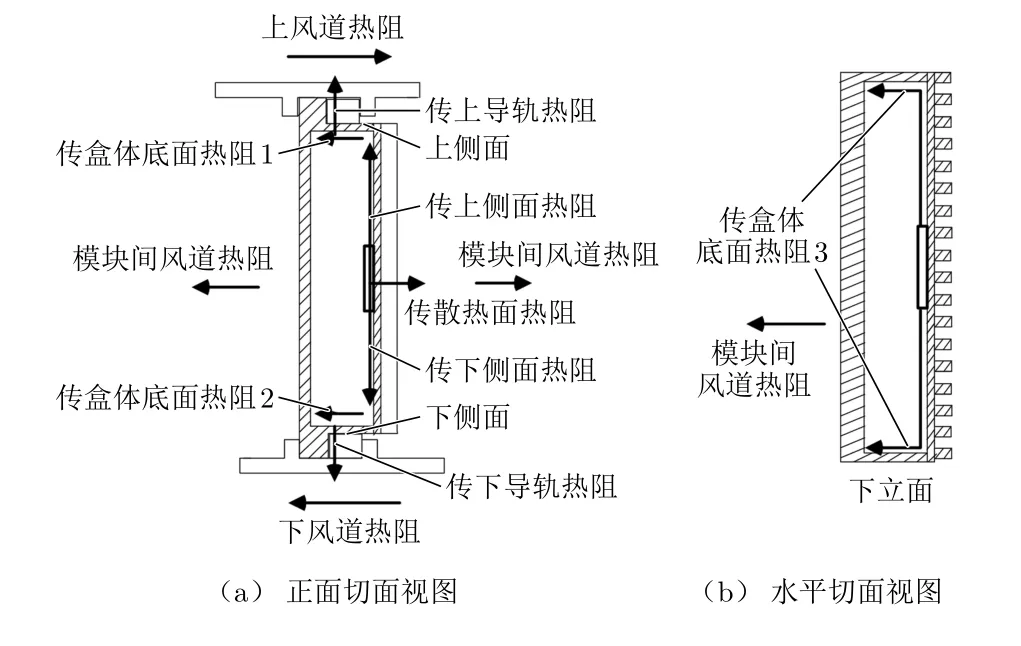
图6 热流示意图

芯片热量从芯片壳体沿着图6所示的各个传热环节传播到冷却空气中。将每个传热环节看作是并联或串联的一个热阻值，可以得到整个开放式风冷机箱的等效热阻网络图，如图7所示。

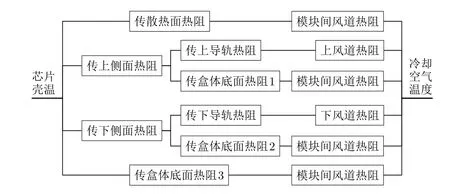
图7 等效热阻网络图

若计算出各传热环节的热阻值，则由此模型可以计算得到整个等效热阻网络的总热阻值，进而通过传导热量和冷却气体的温度求得器件内部的温度。发热器件壳温td的计算公式为：式中：Δt为温度的变化值；tf为冷却空气的温度；Φ为器件的发热功率；R总为整个等效热阻网络的热阻值。

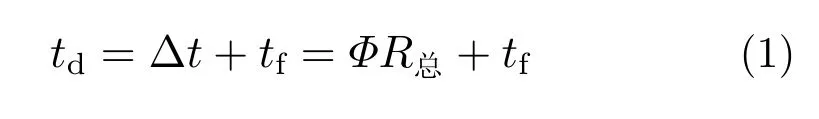
2.2 热阻分析及计算

2.2.1 传导散热热阻值计算

热量在模块壳体中不同方向的传播已被分解为不同的传热环节，故可将模块壳体中的每个传热环节视为一维平壁导热问题。此时，导热平壁热阻Rt的计算公式为[1]：

式中：K为平壁的导热系数；δ为热传播方向的壳体长度；A为与传播方向垂直的截面面积。

接触热阻可以通过查阅相关手册获得。文中各模块的发热器件位于印制板正中的位置，大小为10 mm×10 mm。发热器件顶部与盒体接触处涂有导热脂，导热脂的热阻为Rc1=7×10-6m2·°C/W[8-9]；盖板与盒体的接触及模块与导轨的接触均为在较大压力下的铝合金材料之间的直接接触，其接触热阻Rc2= 5×10-4m2·°C/W。模块所选的锁紧条单侧综合接触热阻为0.3°C/W。

设备的材料为铝合金，材料的导热系数k=117 W/（m·°C）。模块散热面的大小为233.4 mm（长）×160 mm（高），模块壁厚均为2 mm，盖板下嵌到盒体中，接触面宽1 mm，模块总厚度为25 mm。由此可以求得热量由发热器件壳体传导至散热面的热阻值R1：

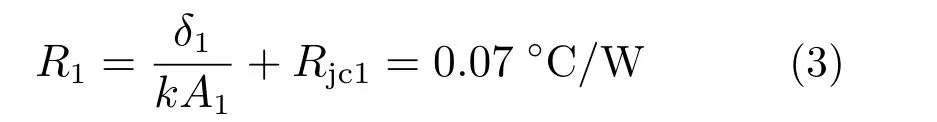
式中：δ1为模块散热盖板的厚度；A1为模块散热盖板的面积；Rjc1为模块内部发热器件与模块壳体的接触热阻。

热量由发热器件壳体传导至上下侧面的热阻值R2和R3为：

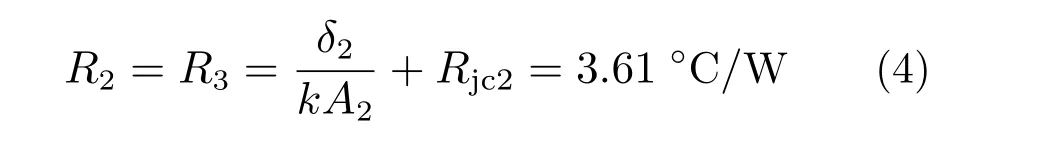
式中：δ2为模块内部发热器件与上侧面的距离；A2为垂直于此热传导路径的模块壳体截面面积；Rjc2为该传热路径上总的接触热阻。

热量由发热器件壳体传导至设备上下导轨通风面的热阻值R4和R5为：

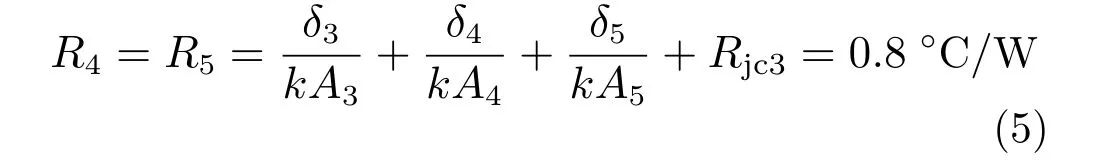
式中：δ3为模块上侧面与模块、导轨锁紧面之间的距离；A3为垂直于此热传导路径的模块壳体截面面积；δ4为锁紧条的厚度；A4为垂直于此热传导路径的锁紧条截面面积；δ5为上导轨的厚度；A5为垂直于此热传导路径的导轨截面面积；Rjc3为该传热路径上总的接触热阻。

热量由发热器件壳体经由盒体上下侧面传导至盒体底面的热阻值R6和R7为：

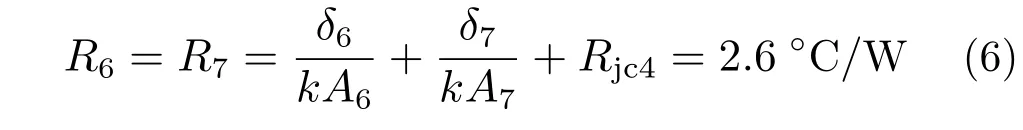
式中：δ6为模块上侧面的宽度；A6为垂直于此热传导路径的侧面截面面积；δ7为盒体底面的厚度；A7为盒体底面面积；Rjc4为该传热路径上总的接触热阻。

热量由发热器件壳体经由盒体立面传导到盒体底面的热阻值R8为：

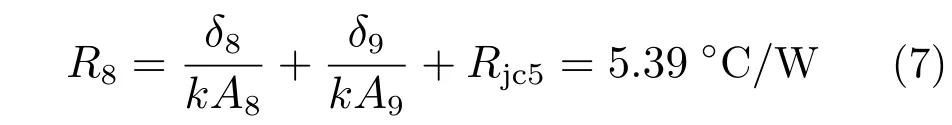
式中：δ8为模块内部发热器件到模块立面的距离；A8为垂直于此热传导路径的模块壳体截面面积；δ9为盒体底面的厚度；A9为盒体底面面积；Rjc5为该传热路径上总的接触热阻。

2.2.2 对流换热热阻值计算

对流换热热阻Rf的计算公式为：

对于强迫对流换热机箱，风道内气体的雷诺数：

式中：ω为风道中空气的流速；d为风道的当量直径；ν为空气在特征温度下的运动粘度。

紊流时，一般取104≤Re ≤105，可以求得考尔本数：

该设备要求在60°C高温下正常工作，由于风机选择所留余量较大，冷却空气进出口温升不高，因此此处取定性温度为60°C。由《电子设备热设计》[1]的附录A可以查得空气的物性参数：质量定压热容cp= 1 005 J/（kg·°C），密度ρ= 1.06 kg/m3，粘度μ=2.05×10-5kg/（m·s），普朗特数Pr=0.696，运动粘度ν=18.97×10-6m2/s。

该机箱选用的风机单台风量为200 m3/h，2台风机的风量共0.111 m3/s，上下风道的入口大小为401 mm（长）×43 mm（宽），可以求得上下风道中空气的流速ω1为：

式中：Q1为风机的流量；S1为上下风道的截面积。

导轨的通风孔一共有13 个，通风孔的大小为218.4 mm（长）×10.6 mm（宽），假设它们之间的风速相等，则模块间风道中的空气流速ω2为：

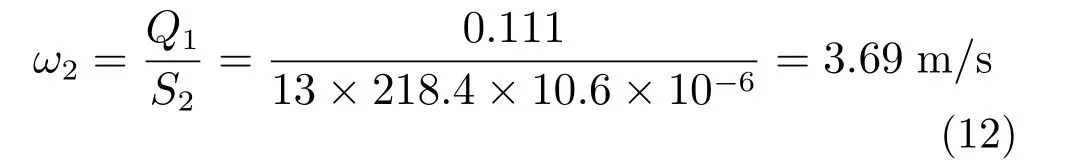
式中，S2为模块间风道的截面积。

上下风道的当量直径d1为：

式中，U1为上下风道的截面周长。

模块间风道的当量直径d2为：

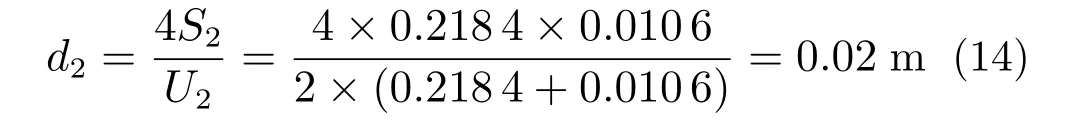
式中，U2为模块间风道的截面周长。

可以得到上下风道中空气的雷诺数Re1为:

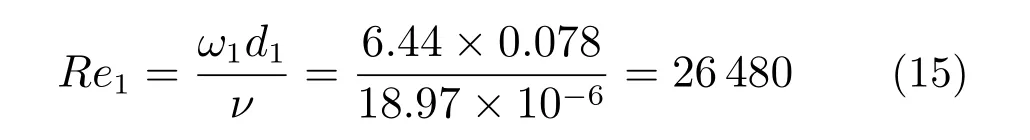
可以求得上下风道中空气的考尔本数J1：

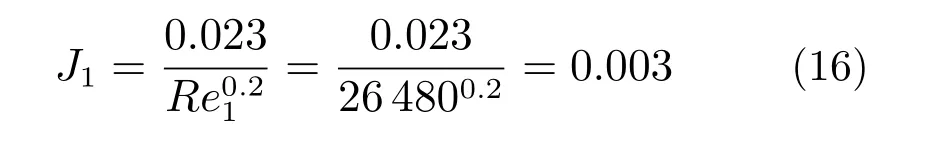
上下风道空气的质量流量G1为：

可以求得上下风道中空气的换热系数hc1：

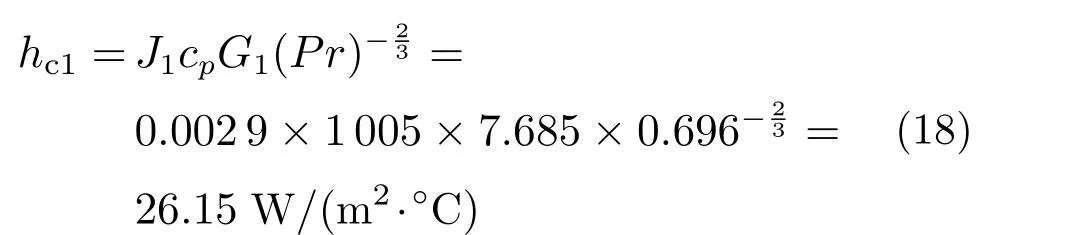
由此得到上下风道中空气的传热热阻Rf1和Rf2：

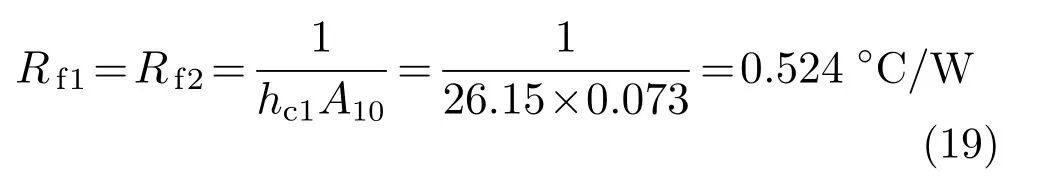
式中，A10为机箱上下导轨的换热面积。

用同样的方法可以得到模块间风道的热阻Rf3：

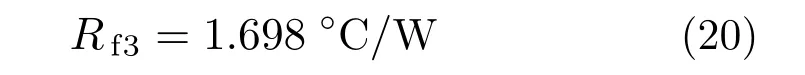
由以上热阻值可算出整个热阻网络的热阻R总：

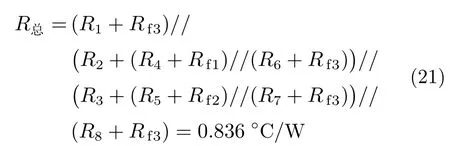
3 仿真验证

根据以往的工程经验，只要仿真条件设置合理，仿真结果与实测结果的误差可以控制在较小的范围内。本文选取软件仿真来验证上述计算结果。

3.1 Flotherm软件仿真

Flotherm采用了成熟的CFD和数值传热学仿真技术，并成功结合了FLOMERICS公司在电子设备传热方面的大量独特经验和数据库，是专业的电子系统散热仿真分析软件。本文选用Flotherm软件对该机箱进行热仿真分析，使用MCAD模块导入模型，并对模型进行了合理的简化：去除造型上的圆角、倒边圆等，保留散热齿和风道的完整造型，用打孔板代替进风孔。简化模型如图8所示。

图8 Flotherm仿真模型图

将环境温度设置为60°C，将流体设置为60°C状态下的空气，按表1从左到右赋予模块发热功率，在组件接触的位置增加接触热阻，在各个模块发热器件表面设置温度监测点。仿真得到其截面的温度云图如图9所示。

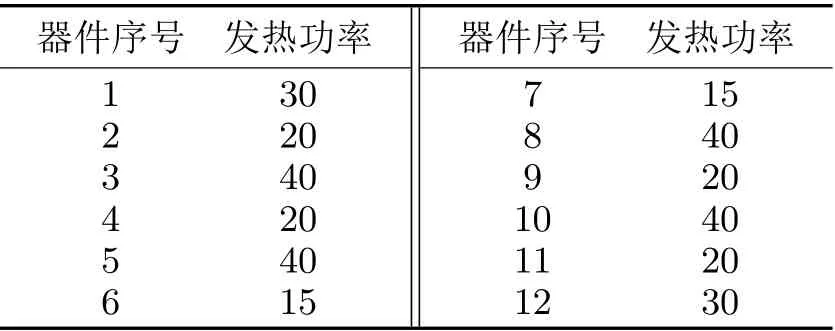
表1 各器件发热功率 W

图9 各模块发热器件所在截面温度云图

3.2 仿真结论

从左到右各模块监测点通过仿真得到的稳态温度和通过等效热阻网络法计算得到的温度对比见表2。

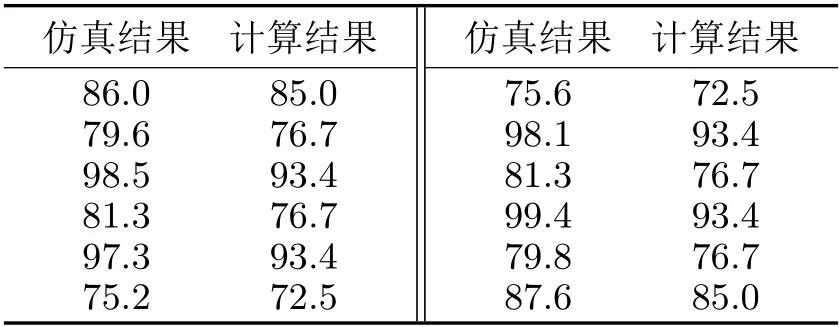
表2 器件温度的计算、仿真结果对比 °C

从表2可以看出，用文中方法计算得到的结果比仿真结果低，但误差不超过8%。

3.3 结论分析

用仿真方法验证计算方法可能存在误差累计的问题，但作为估算方法，总体误差是可以接受的，故此方法可以用于估算设备内部的器件温度。

由于用该方法估算器件温度可行，所以可以用它来降解系统指标，将系统指标转化为模块的设计要求。

现在有些型号的设备由多厂家协同研发。以该型号开放式风冷机箱为例，每个模块拼装到机箱中均可以等效为图7所示的热阻网络模型。若统一每个模块的几何外形和散热齿形式，则模块间风道热阻、上风道热阻和下风道热阻的值就可以视为固定值。此时各模块厂家可以根据图7的模型各自进行散热结构设计而不互相影响。

4 结束语

本文提出了一种等效热阻网络计算开放式风冷机箱内部发热器件温度的方法，并通过软件仿真进行了验证。该方法已应用于其他类系统的某些问题研究，但尚未应用到电子机箱的散热设计领域。

该方法可以用于器件温度的合理估计，也可以将系统指标转化为模块的要求以适应多厂家的协同研发。如果考虑产品系列化，则可将系列产品的热阻网络模型固化，从而将对其散热结构的简单更改视为只修改其中的某个散热环节。

该等效方法可以推广至内插模块、通过模块表面或上下导轨板散热的其他类型机箱以及液冷机箱。

文中计算结果的精确度还有待提高，其原因可能有：1）机箱内部热阻模型仍可以进一步优化，各传热环节的热阻值计算模型还可以更加精确；2）没有考虑辐射散热的影响。