基于支持向量回归的煤粉工业锅炉烟气氧含量预测

杨 晋 芳

(1.煤科院节能技术有限公司，北京 100013； 2.煤炭资源高效开采与洁净利用国家重点实验室，北京 100013；3.国家能源煤炭高效利用与节能减排技术装备重点实验室，北京 100013)

0 引 言

煤粉工业锅炉是近十年来发展起来的1种新型工业锅炉，以其高效、节能、环保等优点代替链条炉并迅速进入市场。烟气氧含量是燃煤锅炉的重要指标之一[1]，其对锅炉的效率和排放有着重要的影响[2-3]，很多学者致力于锅炉氧含量优化的相关研究[4-6]。

目前煤粉工业锅炉烟气氧含量的测量主要通过直接测量方式，借助氧化锆传感器或热磁式传感器测量烟气氧含量[7]，以上仪器可直接显示氧含量的百分比，其反应速度快、测量精度较高，然而也存在以下3个问题:① 价格成本高；② 氧化锆探头在长期使用中会被粉尘堵塞而出现老化现象，严重影响仪器的稳定性和准确性；③ 氧量仪还需定期进行效验。因此，此次研究考虑采用间接测量技术对烟气氧含量进行检测。

间接测量采用软测量的方法[8],即利用易于测量的一些辅助变量以估计主要变量,已在电站锅炉上推广应用并取得较好的效果。采用软测量方法间接获得烟气氧含量，可与仪器测量值比较并对其进行修正，同时可实现对氧含量的实时监控，从而提高锅炉的燃烧效率[9]。

软测量的建模方法主要分为以下4种[10]，分别基于工艺机理分析方法、模式识别方法、人工神经网络方法和支持向量机方法。基于工艺机理分析方法存在滞后，很难符合实际工业现场对监测数据实时性的需求；基于模式识别方法通常与人工神经网络和支持向量机等方法相结合，并应用至实际生产中；基于人工神经网络方法易形成局部极小而得不到全局最优，很多学者针对此项缺点对其进行改进。基于回归支持向量机方法应用于回归估计问题中，得到很好的效果，此方法预测精度很高且泛化能力强。目前已有较多基于此方法进行软测量模型的建立，并已应用至工程实际。但该方法对于大规模训练样本难以实施，建模精度不高。至目前为止，最常用的软测量方法主要包括基于人工神经网络和支持向量机的方法。

针对基于人工神经网络和支持向量机方法的烟气氧含量间接预测技术，已有大量研究并成功应用于电站锅炉。胡世广[11]利用神经网络进行火电厂烟气含氧量的测量并进行建模研究，为火电厂的氧量测量技术提供新手段。马良玉[12]等基于L-M算法改进神经网络模型以更准确地预测烟气含氧量,为实现锅炉的燃烧优化调整、节煤降耗奠定基础。Zhenghao Tang[13]等使用DBN深度学习模型对电厂锅炉氧含量进行预测，结果显示可准确地预测结果。Ma Liangyu[14]等基于ANN对1000MW电厂烟气氧含量进行预测，结果显示此模型可精确预测烟气氧含量，对电厂改善锅炉燃烧、节约能源和减少煤耗具有指导作用。杨秀等[15]采用1种基于粒子群改进的支持向量机算法对氧含量软测量进行建模研究，仿真结果表明预测精度较高、泛化能力良好。任锦等[16]提出改进最小二乘支持向量机模型PSO-LSSVM并对氧含量进行预测，最终仿真结果显示:改进的软测量模型预测精度更高且泛化性更好、模型可靠性更高。Changliang Liu等[17]使用LS-SVM对烟气氧含量进行预测，通过预测值和实际值比较可知，其提出的模型可较准确地预测电厂烟气氧含量。

以上研究均针对电站锅炉，而目前对煤粉工业锅炉氧含量的预测仍很稀少，由此笔者提出煤粉工业锅炉氧含量预测模型，以期为工业煤粉锅炉燃烧系统优化提供指导。

1 现场数据采集

现场数据采集基于煤粉工业锅炉系统的以下工艺流程:煤粉由供料器均匀送入锅炉燃烧器并在炉膛内燃烧，烟气经炉膛内的SNCR(Selective Non-Catalytic Reduction)选择性非催化还原脱硝和尾部的SCR(Selective Catalytic Reduction)选择性催化还原脱硝后，进入NGD(No Gap Desulfurization)半干法脱硫除尘一体化装置进行脱硫除尘，洁净烟气排至烟囱进入大气，锅炉飞灰经仓泵输送至密闭灰塔排出，经封闭罐车运输出厂。

煤粉锅炉DCS(Distributed Control System)分布式控制系统中的历史数据是整个锅炉工艺过程的所有设备测点数据，而氧含量的预测只与部分工艺相关，即进料、燃烧和烟气排放3个过程，因此采集数据时只需筛选出关于3个过程的相关变量即可。

以某矿20 t/h煤粉工业锅炉为研究对象，以20 min为采样时间，采集了采暖高峰期2个月的数据。根据系统机理和工艺流程对变量进行初选，选择了给料频率、引风机频率、炉膛负压、前炉膛温度、省煤器出口烟温等20个变量。以上变量分为控制变量和状态变量两大类。控制变量为技术操作可控制的变量，采集的控制变量为6个，分别为给料频率、补水阀开度、引风机频率、二次风阀开度、进风阀1开度、进风阀2开度。状态变量是反应锅炉状态的一些变量，不能直接控制，初筛包括状态变量14个，分别为蒸汽流量、前炉膛温度、后炉膛温度、一次风压、省煤器入口烟温、省煤器入口水温、省煤器出口烟温、省煤器出口水温、蒸汽压力、二次风流量、炉膛负压、蒸汽温度、炉尾负压、汽包水位。

2 数据预处理和变量筛选

2.1 数据预处理

从现场运行的历史数据库中所采集的数据一般情况下都含有异常数据及干扰数据，其会影响模型的训练，因此需对历史数据进行预处理[18]。此次研究删除异常值和缺失值后，最终得到2 598条数据。

2.2 变量筛选

输入的变量直接影响模型的预测准确性，太多的输入变量将会降低预测精度并增加模型的计算时间，因此有必要将冗余数据去除。通过历史数据集的相关性选择，使用F检验判断每个输入变量和烟气氧含量的关系。F检验、方差齐性检验是用来捕捉每个特征与标签之间线性关系的过滤方法。使用F检验将筛选出与氧含量有着显著关系的变量。通过以下公式(1)和公式(2)计算F值，F值越大则输入变量与氧含量之间的相关性就越大。

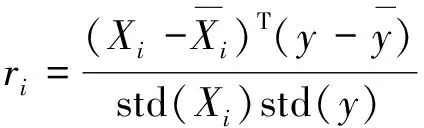
(1)

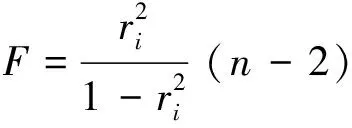
(2)

式中，Xi代表所有样本在i号特征上取值的n维列向量，y是氧含量;ri是样本的相关系数。

经过F检验，从上述20个变量中选取与氧含量关系显著的变量:蒸汽流量、给料频率、后炉膛温度、一次风压、二次风阀开度、进风阀1开度、进风阀2开度、省煤器入口烟温、引风机频率、蒸汽压力、炉膛负压、二次风流量、炉尾负压、蒸汽温度14个变量，其中控制变量5个，状态变量9个。

2.3 数据标准化

从DCS中采集的历史数据，其各变量有着不同的单位，一些变量大小在数值上相差很大，有的甚至达到几个数量级。为了不影响模型的精度，需要将采集到的数据进行Z-score 标准化，以消除因为数据数量级相差大造成的变量对模型作用差异大。

Z-score标准化公式详见如下公式(3):

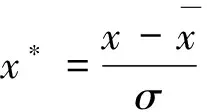
(3)

经过Z-score标准化的所有数据都聚集在0附近，方差为1，经过处理后的数据不会造成因数据的数量级差异而影响模型精度等问题。

3 建立模型

3.1 支持向量回归(SVR)

支持向量机是用于分类的算法，支持向量也可用于回归，称之为支持向量回归(SVR)。支持向量机可分为支持向量分类和支持向量回归[19]，支持向量回归因其优越的学习性能，使其在系统辨识、预测估计等领域被广泛研究应用。文中预测氧含量值，采用支持向量回归算法。

给定数据集:D={(x1,y1),(x2,y2),……,(xn,yn)},yn∈R，且令:

f(x)=wTx+b

(4)

w和b是待确定的模型参数，T为转置符号，希望学得1个回归模型,使得f(x)与y尽可能接近。假设能容忍f(x)与y之间最多有ε的偏差，如图1所示。

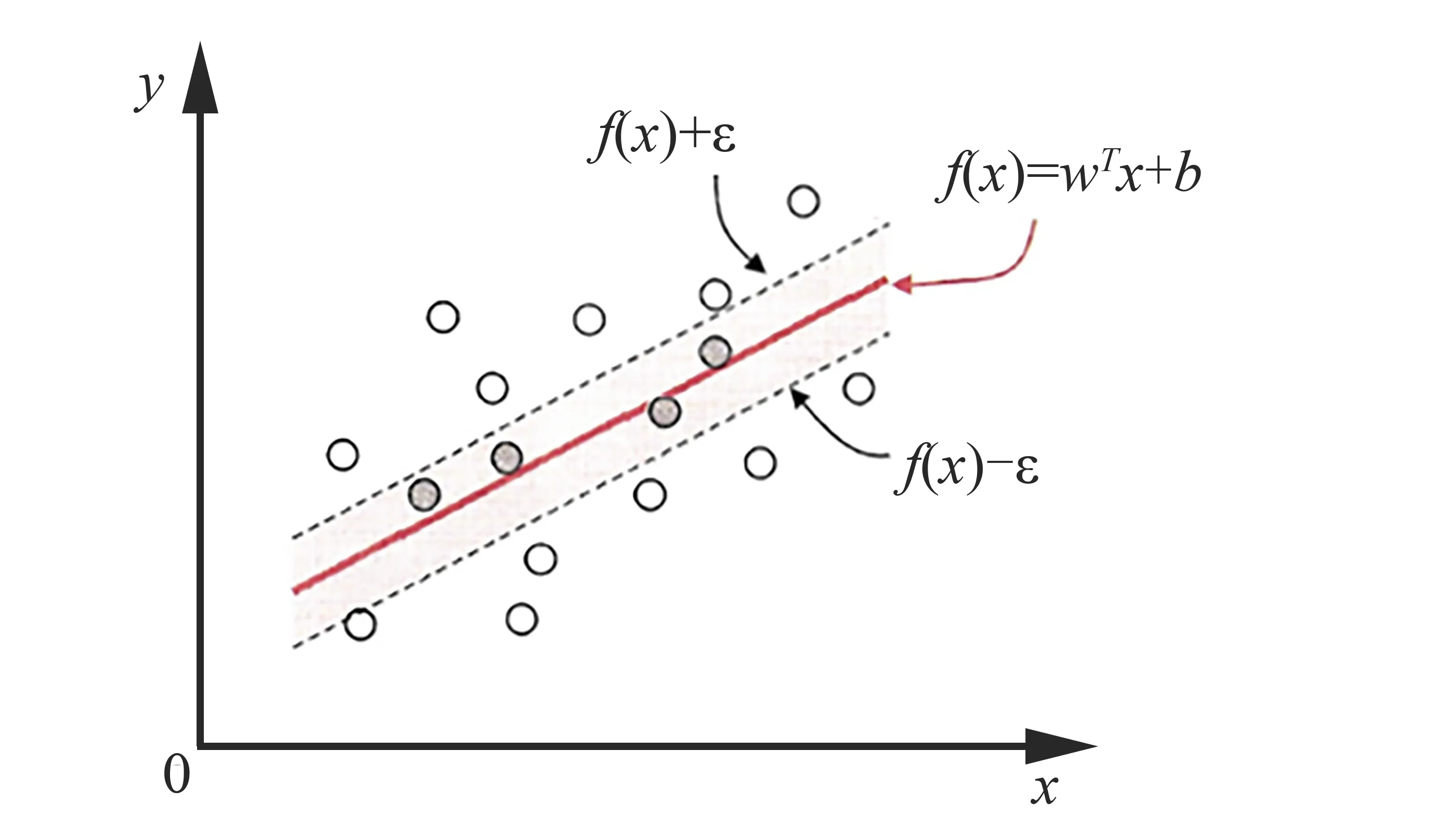
图1 支持向量回归模型原理图Fig.1 Schematic diagram of support vector regression model

即仅当f(x)与y之间的差别绝对值大于ε时才计算损失。于是，SVR问题可形式化为:

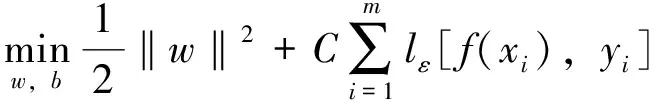
(5)

式中,C为正则化常数;lε是图1中所示的ε-不敏感损失函数:

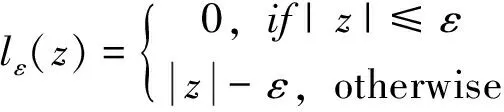
(6)

引入松弛变量和拉格朗日乘子，最终可解得SVR为:

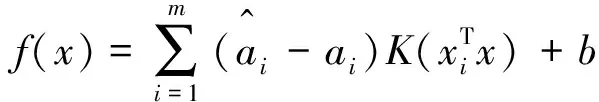
(7)

3.2 建立模型

上文经过F检验已筛选出14个变量，其中控制变量5个、状态变量9个。模型中的变量见表1。考虑到输入变量的性质，将模型训练分为控制变量、状态变量以及两者合并3种方式，并分别对3个训练的模型依次进行测试。

表1 模型中的变量详情Table 1 Variables details in model

3.3 模型训练与预测

将经过处理的2 598条数据的70%作为训练集，建立控制变量、状态变量以及两者合并的支持向量回归模型并进行训练，30%作为测试集测试模型的性能。3种情况下烟气氧含量软测量模型的预测结果分别如图2、图3和图4所示，蓝色实线代表直接测量所得的真实值，桔色虚线代表预测值。

从图2～图4可看出，3种软测量模型的烟气氧含量预测值均能较为准确地反映真实值的变化趋势。

将图2与图3和图4分析比较可知，图2预测值与真实值差距偏大，控制变量调节后可即时反馈到从DCS中取得的数据上，例如给料频率从20调整为10，取得的历史数据显示为10，而实际锅炉工况需要一定的时间才能基本稳定地运行在给料频率为10的工况。因此若取到此组数据，瞬时取到的氧含量值有一定的误差。故若只基于控制变量来预测模型，结果和直接测量之间的误差较大。而基于状态变量的预测结果符合最佳，出现以上现象是由于状态变量较控制变量有一定的延迟，和直接测量得到的氧含量较为同步。对于基于控制变量和状态变量两者合并的SVR模型，其准确度介于两者之间。

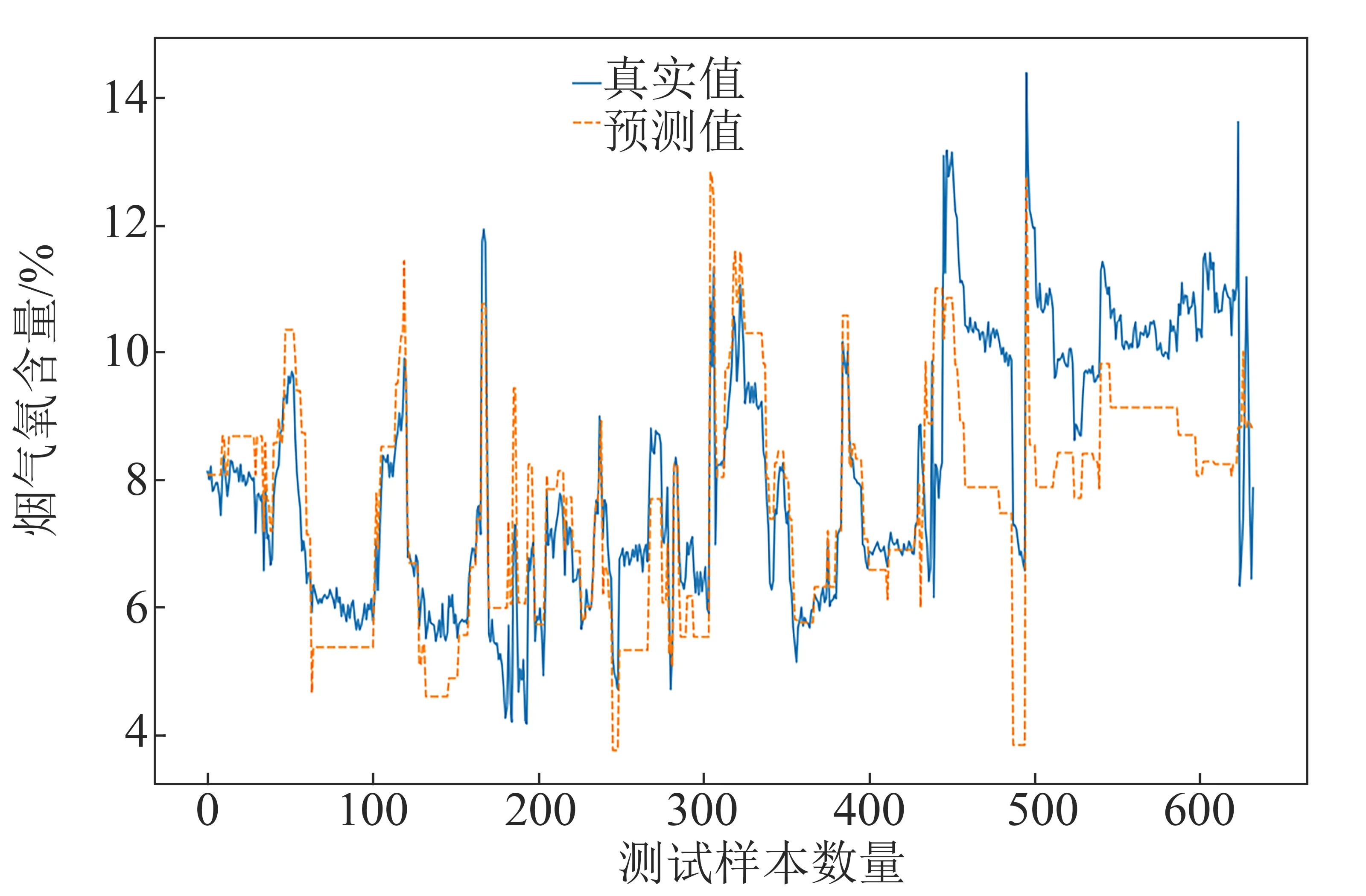
图2 基于控制变量的预测值与真实值比较Fig.2 Comparison of prediction values and real values based on control variables

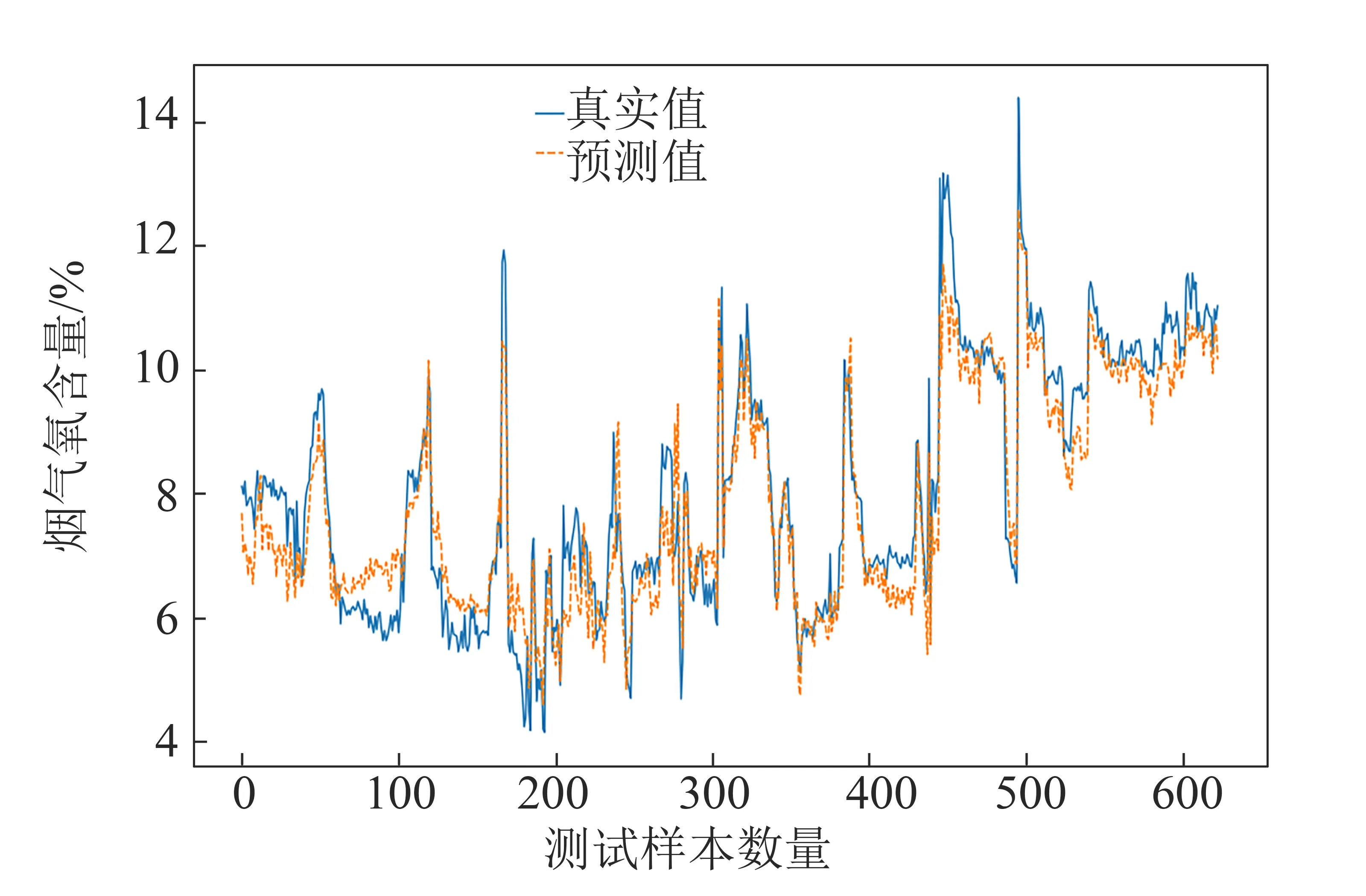
图3 基于状态变量的预测值与真实值比较Fig.3 Comparison of prediction values and real values based on state variables

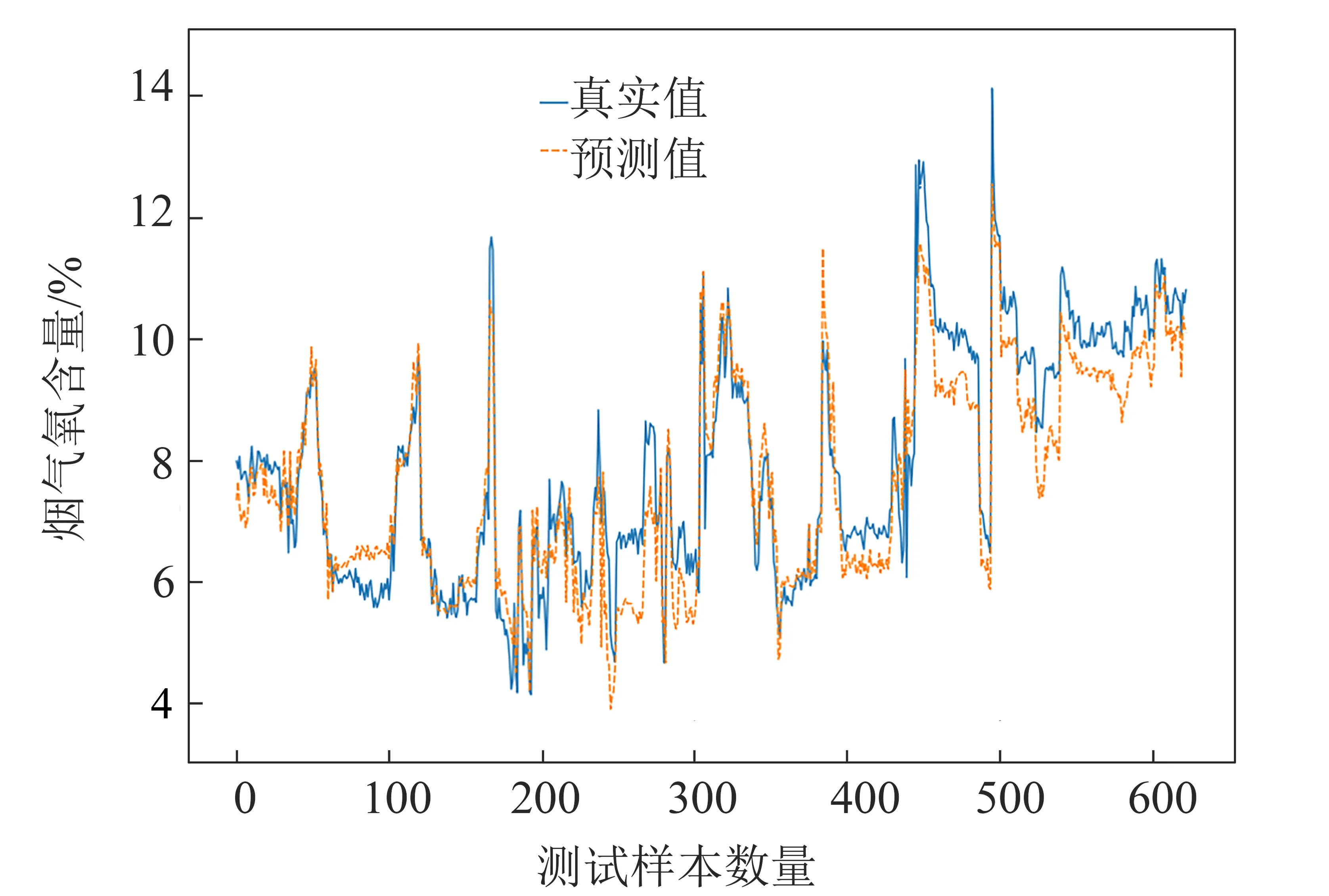
图4 控制变量和状态变量合并的预测值与真实值比较Fig.4 Comparison of prediction values and real values based on both control and state variables

3.4 模型评价

为了评价预测模型，使用均方误差(MSE)、平均绝对误差(MAE)和决定系数(R-Square)来衡量预测模型的性能[20]，其计算见公式(8)～公式(10):

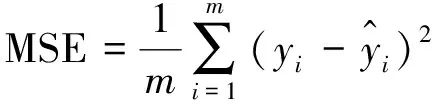
(8)

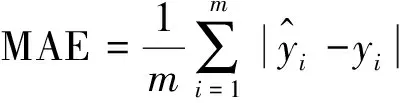
(9)

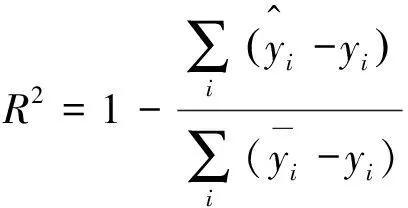
(10)

式中m——测试数据的样本数量，个；

yi——烟气氧含量真实值，%；

对测试结果分析详见表2，MSE和MAE的值越小，说明模型精度越高。而R2取值范围为[0,1]，R-Squared越大，表示模型拟合效果越好。评价指标进一步说明基于状态变量的SVR模型效果最佳。

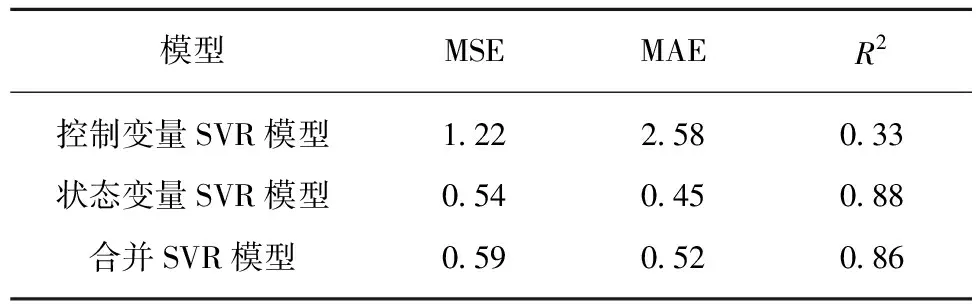
表2 模型评价指标Table 2 Model evaluation indicators

4 结 语

煤粉工业锅炉的燃烧工况较为复杂，而直接测量氧含量仪器成本高，还受到锅炉运行积灰等影响，因此软测量越来越受到人们的重视，也逐渐应用至实际工业生产中。烟气氧含量预测技术已在电站锅炉上得以推广应用，对在工业锅炉上的应用具有借鉴意义。

为了解决工业锅炉的氧含量软测量问题，笔者提出了支持向量回归模型对工业锅炉的烟气进行氧含量测量。整个预测模型分为以下3个部分:

(1)选取烟气氧含量的主要影响变量并将其对应的数据标准化，使用了F检验筛选出对氧含量有显著影响的变量，最终选取14个变量作为输入，为了防止因不同的变量数值上数量级相差较大进而造成训练模型时各变量作用相差巨大，对输入数据进行Z-score标准化。

(2)建立模型。将第一步选出来的变量分为控制变量和状态变量，并运用SVR理论构建分别基于控制变量、状态变量和两者合并的氧含量预测模型，结果表明3种模型的趋势与测量值一致，基于状态变量SVR模型优于其它两者，基于状态变量的模拟结果能较好地预测实际值的趋势，为工业煤粉锅炉燃烧系统优化提供指导。

(3)模型评价。为了评价预测模型，使用均方误差、平均绝对误差和决定系数来衡量预测模型的性能，进一步证明了基于状态变量的SVR模型效果最佳。