基于IR-UWB 信号特征匹配的空间TDOA 系统的设计及LOS 环境下的误差分析

李 虎，高 路，白锦良，刘佳琪，孙 恒

（北京航天长征飞行器研究所，北京，100076）

0 引 言

当前再入飞行技术日新月异，为了满足对位置服务的需求，各种定位技术不断发展。其中空间目标定位作为最常见的定位应用，一直受到业界的重视。由于空间目标定位系统有着自身的特点，需要结合具体情况进行分析和设计，并不能完全照搬一些定位技术。实用的空间目标定位技术至少满足以下条件：a）抗干扰能力强；b）生产成本低；c）系统功耗低；d）收发器体积小。目前，常见的目标定位技术包括有GPS 辅助（A-GPS）技术、射频识别技术（Radio Frequency Identification，RFID）、无线局域网（Wireless LAN，WLAN）和冲激无线电-超宽带（Impulse Radio-Ultra Wideband，IR-UWB）技术等[1,2]。

其中，IR-UWB 技术具有以下优点：a）IR-UWB信号无载波，不需要调制解调，所以收发系统简单，生产成本低；b）IR-UWB 信号为纳秒或亚纳秒级别的窄脉冲，时间分辨率非常高，平均功率较低。所以，IR-UWB 技术结合基于到达时间的测距技术（例如时差定位）能够充分利用时间分辨率高的特点[3]，特别适合定位系统，在近几年得到了广泛的研究[4,5]。

对于定位系统来说，其定位误差分析都是系统设计中的关键部分。时差定位（Time Difference of Arrival，TDOA）方法广泛应用于地面与空间等定位系统中，系统组成的探测网络由若干接收器组成，系统通过处理多个测量站采集到的信号到达时间数据对IR-UWB 的发射器进行定位。发射器发出的IR-UWB 信号到达任意2 个接收器的时间的差值确定了一对以2 个接收器为焦点的双曲面，为了获得发射器的三维坐标，需要至少4 个接收器产生3 对双曲面，交汇解出辐射源的位置。在发射器某一坐标信息（如高度信息）可提前预知的情况下，采用3 个接收器或更少接收器测量也可以求得发射器的三维坐标。对于TDOA 系统的误差分析采用类似文献[6]的技术手段，其噪声建模为单一的高斯白噪声（本文中称为“总体时差噪声”）。但是在实际系统中，在系统的不同部分存在不同类型的噪声，用单一的高斯白噪声直接建模过于粗略，对系统设计的指导意义不够明确。本文通过对实际系统的分析，将在工程中对实际系统精度影响较大的3 种误差（位置误差、时差量测误差、时间同步误差）进行建模并分析，得到他们与定位精度的数量关系并进行仿真，以便指导实际系统的设计。

1 定位模型

基于IR-UWB 信号特征匹配的TDOA 系统分为发射器、接收器和位置解算器3 个部分，以坐标轴建立笛卡尔坐标后，系统结构如图1 所示[7]。

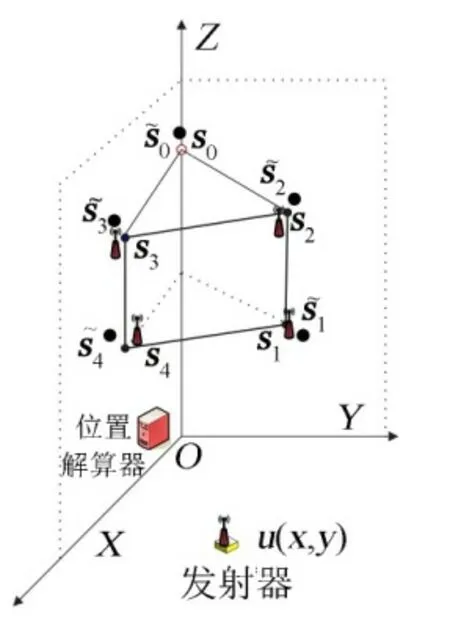
图1 系统结构示意Fig.1 System Configuration

系统中的M个发射器位于地面，间断的循环发射IR-UWB 信号，不同发射器的IR-UWB 信号的特征不同。系统中的N个接收器（编号分别为 0,1,...,N-1）位于空间，用于接收发射器发出的无线信号，其位置已知且固定。接收器的真实位置记作si=[xi,yi,zi]T，由于误差影响，得到的接收器的位置记作is～ 。其中1个接收器作为主站（位置为s0），其他N-1 个接收器用作副站。主站和副站的区别在于主站具有时间模块，副站用有线方式通过主站获得时间。只在主站中放置时钟模块的原因：一是为了减少模块个数，可以节省成本；二是TDOA 系统是靠时间差来定位的，如果副站也放置时钟模块，对时钟模块的同步要求比较高，只采用1 个时钟模块无需同步，节省成本。

发射器和接收器之间通过无线进行信号传输，接收器和位置解算器之间通过有线方式传递信息。主站和副站利用特征匹配的定位算法[8,9]，根据IR-UWB 信号的特征与发射器的特征进行匹配，并将识别结果（包括发射源编号和到达时间（Time of Arrival，TOA））通过有线传输方式传送给信号处理器。信号处理器综合主站和N-1 个副站给出的识别结果，利用TDOA 算法解算出各发射器位置。信号处理流程如图2 所示。

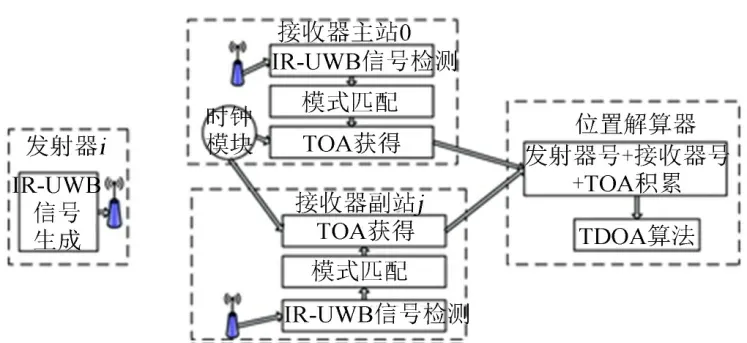
图2 信号流程Fig.2 Signal Processing

2 误差分析

本节分析在第1 节中设计的TDOA 系统的定位精度和误差的关系。只考虑了视距（Line of Sight，LOS）环境下的结果，对于超视距环境（主要考虑阴影效应和多径效应）下的精度只会更差。从这个角度看，给出的结论是定位精度的一个上界。第1 节中给出的系统在工程中常见的误差包括站间时间同步误差、到达时间量测误差和位置误差。定位误差与总体时差误差、观测站和目标相对位置有关，可以分为直接时差误差和间接时差误差。直接时差误差包括时间同步误差、时差量测误差；间接时差误差主要由观测站的位置误差引起。由前文可知影响精度的主要因素包括：站构型（包括基线长度）、站间时钟同步精度、自定位精度、对脉冲到达时间的测量精度，这些因素与精度之间定性的关系如表1 所示。在本节进行定量分析，上述因素都可转化为“总体时差误差”进行统一分析。

表1 系统误差影响因素分析Tab.1 Analysis of System Error

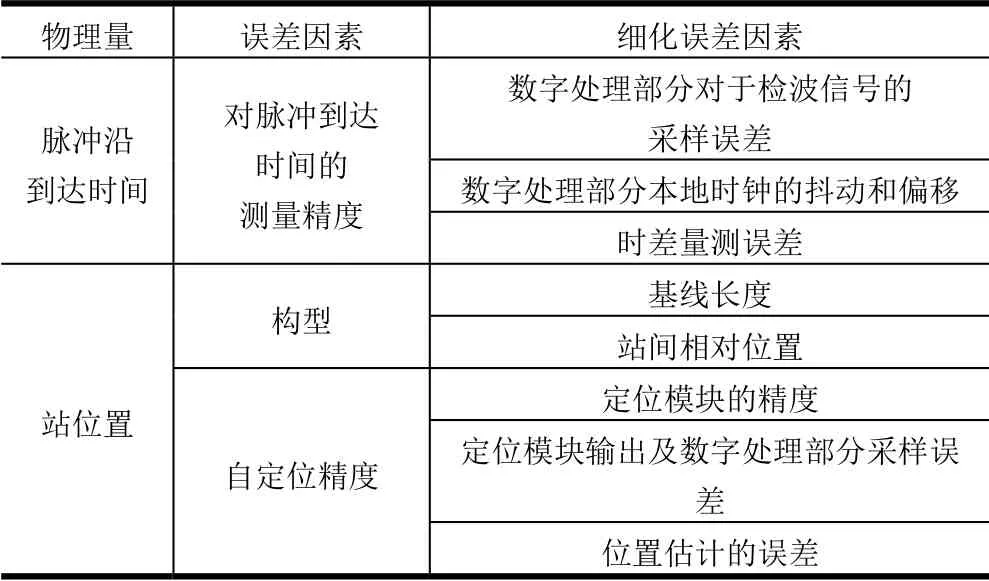
续表1

站间时间同步误差是指2 个接收器时间同步引起的误差，用Δtsys表示，可假定为方差为的高斯白噪声。到达时间量测误差与时差测量方法有关，可假定为方差为的高斯白噪声。位置噪声由接收器自身位置误差引起，包括接收器在x,y,z3 个方向上的误差，用Δs表示。下面分析中假定位置测量误差各向同性，建模为协方差阵为的白高斯随机矩阵，I为3 × 3的单位阵，σs为接收器位置误差半径平方的均值。

分析误差分量与总体时差噪声的关系。由图1 可知，以主站和副站1 为例，研究接收器位置误差、站间时间同步误差和到达时间量测误差对时差测量精度的影响。假定发射器位于u=[x,y]T处，于t0时刻发射了1 个脉冲，主站和副站1 在s0和s1处接收到信号的时间分别为tr0，tr1：

式中c为光速；主站测得的到达时间tr0的实际测量值为trm0：

式中 Δt0为主站的时间量测误差，假定它是服从均值为0、方差为的高斯分布的随机变量。副站1 测得的到达时间tr1的实际测量值为trm1：

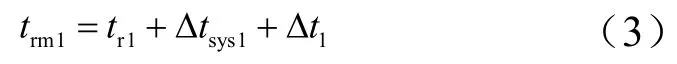
式中 Δtsys1为副站1 与主站的时间同步误差，假定服从均值为0、方差为的高斯分布；Δt1为副站1 的时间量测误差，假定它是服从均值为0、方差为的高斯分布的随机变量。

由于接收器的真实位置不能确定，只能得到含有误差的主站和副站1 的坐标矢量和：

即：

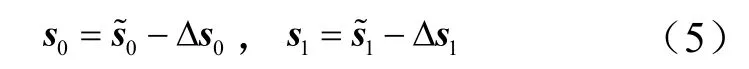
式中 Δs0和Δs1分别为主站和副站1 的位置测量误差。

就单个时差量测值τm1=trm1-trm0而言，有：

上式只含有未知的位置参数，其余参数是已知的。式（8）中 Δτ1为总的时差测量误差，表达式为式（9）。

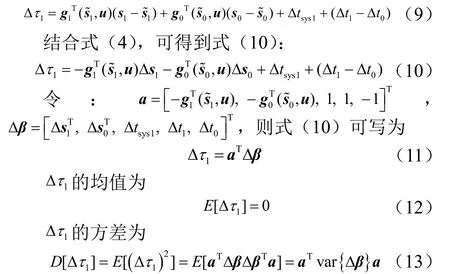
假定接收器位置测量误差、时间同步误差、时间量测误差之间相互独立，则Δβ的协方差矩阵可表示为式（14）。将式（14）代入式（13），可得式（15）：

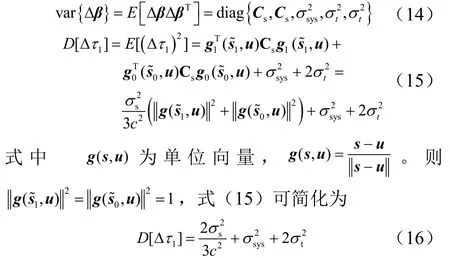
由式（16）可知，总体时差误差的方差D[ Δτ1]与接收器位置误差、站间时间同步误差以及到达时间量测误差有关，而与接收器的位置和发射器的位置无关。

总体时差误差的均方根误差 1τσ为

式（17）的直观意义为：时差量测误差对于时差的影响是双重的，所以其方差的因子为2；位置误差对于时差的影响需要乘以光速的倒数转换为时间，并且也是双重影响，所以其方差的因子为22；时间同步误差是各个副站对于主站的误差，其方差的因子为1。

结合文献[3]的结论，协方差矩阵Pu为

由式（18）可知，除了上述3 种误差对于CEP 有影响之外，布站也会通过影响矩阵H来影响精度。

根据协方差矩阵Pu也可以确定定位误差椭圆关于x,y的方程为

式中ρ为协方差矩阵中系数；D2=-2 ln(1 -P)；通常将P=0.5所对应的椭圆称为椭圆概率误差，此时D= 1.1774；为目标位置估计值。定位误差椭圆的参数包括半长轴a、半短轴b和长轴方向θ。当ρ=0时，式（19）变为

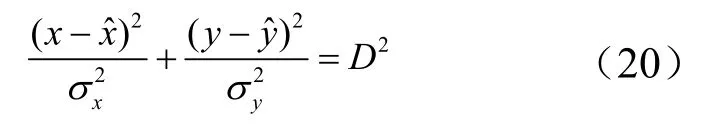
根据σ x,σy可直观得到定位误差椭圆的参数：

当ρ≠ 0时，作坐标变换：

式中u，v为新坐标系中坐标变量；定位误差椭圆在新坐标系下的表达式变为

3 数值仿真

对于图1 中的系统，按照上述分析的结论进行精度的仿真。

首先分析总体时差误差各因素的影响关系。当位置误差和时间同步误差固定时，时差量测误差随时间测量误差的变化关系如图3 所示。由图3 可知，总体时差误差随着时间量测误差的增大而增大，当时间量测误差较小时，观测站位置误差和时间同步误差主要影响总体时差误差，当时间量测误差较大时，时间量测误差对总体时差误差的影响较大。

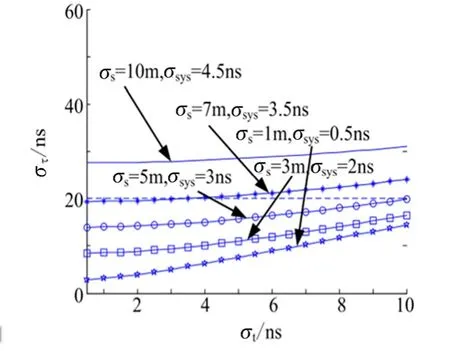
图3 总时差误差随与时间测量误差的变化关系Fig.3 Total TDOA Error v.s.Time Measurement Error

当位置误差和时间量测误差固定时，总体时差误差随时间同步误差的变化关系如图4 所示。由图4 可知，总体时差误差对时间同步误差不敏感，即当观测站位置误差和时间量测误差确定后，提高时间同步精度对提高时差测量精度贡献并不大。

图4 时差测量误差随时间同步误差的变化关系Fig.4 TDOA Error v.s.Time Synchronization Error

仿真假设接收器数量为5 个，其中主站坐标为[0,0,3]，4 个副站的坐标分别为：[2,0,2]、[2.5,0,2]、[0,2,2]、[0,2.5,2]（上述坐标中数值单位均为km）。

当接收器位置误差为0.01 m，时间同步误差为3 ns，时间量测误差为2 ns 时，仿真结果如图5a 所示；当接收器位置误差为0.1 m，时间同步误差为4 ns，时间量测误差为8 ns 时，仿真结果如图5b 所示。

图5 不同系统误差下系统的精度CEP 分布Fig.5 CEP v.s.System Error

从图5 可以看出，距离接收器越远的位置，定位精度越差。此外还可以看出，系统中的误差指标越差，会导致定位精度的恶化。需要结合具体系统指标对站址布局等因素进行合理优化。

4 结 论

本文给出了基于IR-UWB 信号特征匹配的TDOA系统的原型和初步设计，并且对于LOS 环境下，针对实际系统设计过程中最常见也是对精度有直接而重要影响的3 类误差：位置误差、时差量测误差、时间同步误差，进行了分析，得到了其与总时差误差的数量关系。最后对1 个实例系统进行了CEP 仿真，得到上述误差对于系统精度影响的直观概念。在实际系统设计中，应当根据系统的经费预算和各个分系统的性能指标合理进行参数分配。并应针对房屋的不同结构，选择不同的接收站结构布局设计，以便在允许的经费范围之内实现对重要区域达到比较高的精度。