绳驱准连续型机械臂的动力学研究

黄玉平，贾龙飞，郭亚星，陶云飞，郑继贵

（1.北京精密机电设备研究所，北京，100076；2.航天伺服驱动与传动技术实验室，北京，100076）

0 引 言

在诸多领域中，定期的监测和维护是确保设备安全工作的重要方式，但由于此类设备具有复杂的结构，使得可供监测及维护作业的空间非常狭小，维修人员不易进行操作。为了顺利完成狭小空间中设备的监测和维护，机械臂被用来代替人类进行作业。此类机械臂需要具备穿越狭窄环境、回避障碍物的能力，并具有足够大的灵巧操作空间。

准连续型机械臂具有多个自由度，可呈现多种运动模式，可在狭小、复杂及非结构化的环境中执行任务[1]，且具有多目标优化能力，广泛应用于航天[2]、航空[3]、特种加工、核电站监测[4]、医疗[5]和灾害救援[6]等领域。由于准连续型机械臂采用绳索驱动的方式，具有多个自由度，而且驱动绳和臂杆之间存在摩擦力，为实现准连续型机械臂的精确控制，故需建立准确的动力学模型。

常用的动力学建模方法包括牛顿欧拉法[7]、Schiehlen 法[8]、Kine 法、拉格朗日法[9]等，其中拉格朗日法借助广义坐标，可极大简化建模过程，因此在实际工程中应用广泛。但如果模型中的自由度超过6 个或更多，则会大大增加拉格朗日方法的运算量，在实际应用中无法满足实时控制的要求。递归牛顿欧拉法在多个自由度的问题上，具有较小的运算量，故广泛用于建立准连续型机械臂的动力学建模。

针对准连续型机械臂的动力学研究，Yuan[10]建立了一种连续型机械臂的静力学模型，验证了在机械臂偏转角度较大的情况下，摩擦力对机械臂的运动精度影响较大。Rone[11]利用虚功率原理建立了绳驱连续型机械臂的静态动力学摩擦模型，在不考虑惯性效应的情况下推导了静力平衡模型。马曙光[12,13]利用空间算子代数方法推导了机械臂的动力学方程，对动力学模型中的绳索模型进行改进，通过增大仿真时间步长临界值来提高动力学模型的数值仿真效率，可实现实时仿真，但未给出具体的关节力矩与驱动绳拉力的转换关系，并未对最优化问题展开分析。刘天亮[14]针对绳驱动超冗余机械臂建立了动力学模型，并给出力矩与驱动绳拉力的转换关系，但建立的动力学模型较为复杂，且利用该方法得到的驱动绳拉力变化曲线不光滑。

准连续型机械臂具有多个自由度，因此本文采用递归牛顿欧拉法进行动力学建模分析。通过确定机械臂运动过程中，各变量之间的转换关系，在考虑摩擦力的前提下，建立了完整的动力学模型。并针对关节力矩与驱动绳拉力之间的转换，优化了最优化模型中的目标函数，采用置信域算法解决了24 根驱动绳拉力值曲线的不光滑问题，并通过降元进一步缩减了计算时间。

1 动力学建模

1.1 机械结构

本文所研究的准连续型机械臂如图1a 所示，主要包括机械臂本体结构、驱动机构、导轨。机械臂本体结构由8 个刚性臂杆串联而成，臂杆之间通过十字轴万向节连接，驱动机构由伺服电机、联轴器、滚珠丝杠、滑块组成。伺服电机带动丝杠转动来控制滑块移动，从而拉动驱动绳，进一步可通过控制驱动绳产生的位移及拉力来调整机械臂的姿态。

每一组驱动机构控制一根驱动绳，与驱动绳数量相同的24组驱动机构以圆周阵列的形式均布于驱动机构中的基座上。穿过孔ija、孔ijb、孔ijc 的3 根驱动绳驱动第j（j=1,2,…,8 且j≥i）个臂杆，在第i个臂杆的圆形截面上取驱动绳穿过孔ija、孔ijb、孔ijc 的圆心与该圆形截面圆心连成的直线与Zi轴之间的夹角为该点的位置角度φija、φijb、φijc。如图1c 中的孔41a、孔47a、孔43c 的位置角度分别为0、90、270 。

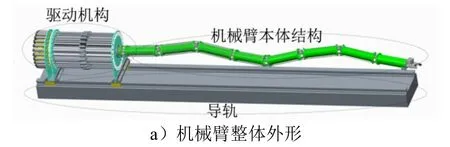
图1 准连续型机械臂结构示意Fig.1 Schematic Diagram of Quais-continuous Manipulator

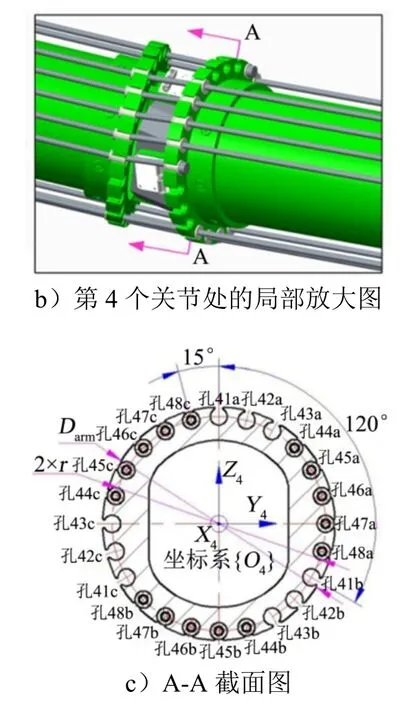
续图1

1.2 运动学分析

准连续型机械臂模型基于以下假设：

a）每节臂杆为刚体；

b）驱动绳不可伸长，且质量和惯量很小。

图2 为基座的本体坐标系{O0}以及8 个臂杆的本体坐标系{O1}～{O8}。本文建立相对于地面固定不变的世界坐标系{Oxyz}，当8 个臂杆的轴线在同一水平方向时，以8 个臂杆的轴线方向为X轴方向，以重力的反方向为Z轴方向，Y轴方向可根据右手定则确定。

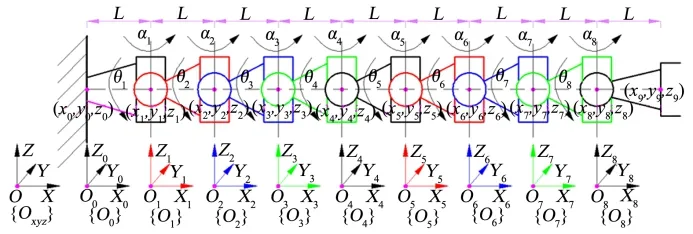
图2 机械臂的D-H 坐标系Fig.2 The D-H Coordinate System of Manipulator

第i个臂杆具有2 个自由度，分别是相对于第i-1个臂杆的偏航角αi和俯仰角θi，坐标系{Oi-1}先沿着Xi-1轴平移L，再绕Zi-1轴旋转αi，最后绕Yi轴旋转θi转换为坐标系{Oi}。可得到转换矩阵为

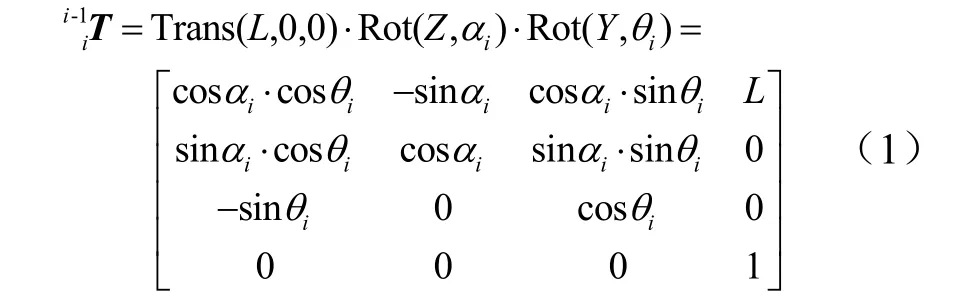
在转换矩阵的基础上可推导出各驱动绳长度、关节角度、臂杆末端点等数据之间的转换关系，即可建立准连续型机械臂完整的运动学模型。

1.3 动力学分析

1.3.1 单臂杆受力分析

下面在第i个臂杆的本体坐标系{Oi}中，对其进行受力分析，得到如图3 所示的单臂杆受力分析图。

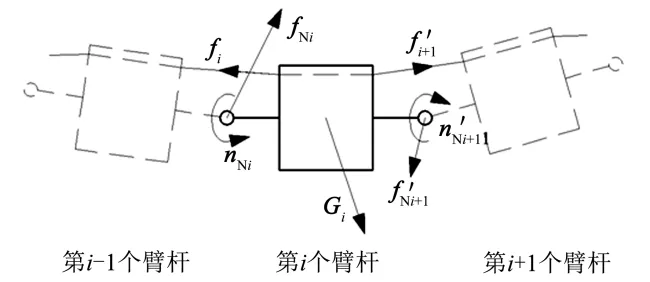
图3 单臂杆受力分析Fig.3 Force Analysis of the Single Arm

图3 中的力和力矩都为第i个臂杆本体坐标系{Oi}中的力和力矩，根据力平衡及力矩平衡，可得：

图4 单臂杆简化受力分析示意及局部放大图Fig.4 Simplified Force Analysis of the Single Arm and Local Enlarged View

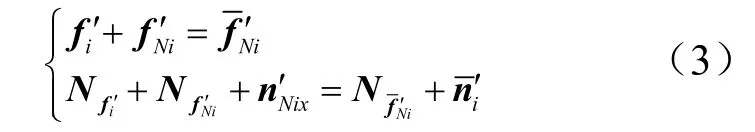
合并式（2）和式（3），可得式（4）。

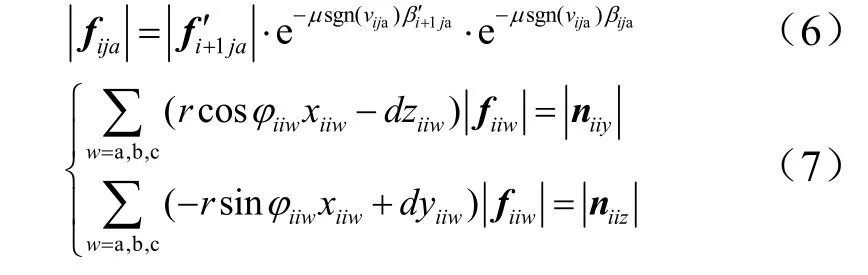
基座运动的力由直线导轨提供，用符号F0表示。由于有末端外力Fe及自身重量Gi的影响，需要24 根驱动绳提供驱动力，进而转换为驱动力矩，来维持整个系统的平衡。fiia、fiib、fiic为第i个臂杆的3 根驱动绳的拉力，合力为fii。fija、fijb、fijc为第i个关节处驱动第j个臂杆的3 根驱动绳的拉力，合力为fij。为驱动第i+1 至第8 个臂杆的绳子在第i个关节处的合力。通过第i个关节的3×(9-i)根驱动绳在第i个关节处的合力为fi。以上各力可通过式（8）进行转换。niiy、niiz为驱动绳拉力fii等效至Yi轴、Zi轴的力矩，为等效至Yi轴、Zi轴的力矩。niix、niiy、niiz的合力矩为nii，的合力矩为，通过第i个关节的所有驱动绳在第i个关节处的合力fi平移至坐标系{Oi}原点产生的合力矩。以上各力矩可通过式（9）进行转换。

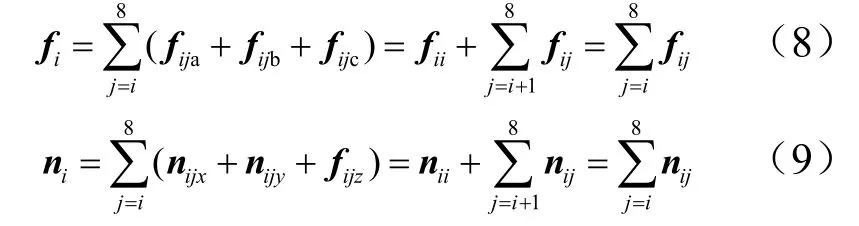
1.3.2 数学模型建立

牛顿欧拉法是一种基于牛顿方程及欧拉方程分析矢量力学的方法，可采用递归方法计算准连续型机械臂的动力学参数。牛顿欧拉法的递推由两部分组成：第1 部分为正向递推，从基座到第1 个臂杆，然后到第2 个臂杆，依次往后，直至第8 个臂杆，由式（10）可计算每个臂杆的角速度、角加速度及质心加速度；第2 部分为反向递推，从第8 个臂杆到基座，由式（11）反向计算作用力和力矩及关节驱动力矩。本文需要将关节驱动力矩等效转换为驱动绳的驱动力矩。

式中mi和Ici分别为第i个臂杆的的质量和质心的惯性张量。

综上可得准连续型机械臂各参数转化示意，如图5所示。图5 中包括运动学与动力学2 大模块，运动学模块主要分为3 个小模块，分别为求解旋转矩阵及平移矩阵、求解驱动绳在每个位置的方向以及求解驱动绳与臂杆轴线的夹角及驱动绳相对于臂杆的速度。动力学模块主要分为4 个小模块：利用牛顿方程求解质心加速度等参数、利用欧拉方程求解合力矩等参数、利用最优化算法将二力矩转换为三绳拉力、利用摩擦力公式计算绳子在不同位置处的拉力大小。

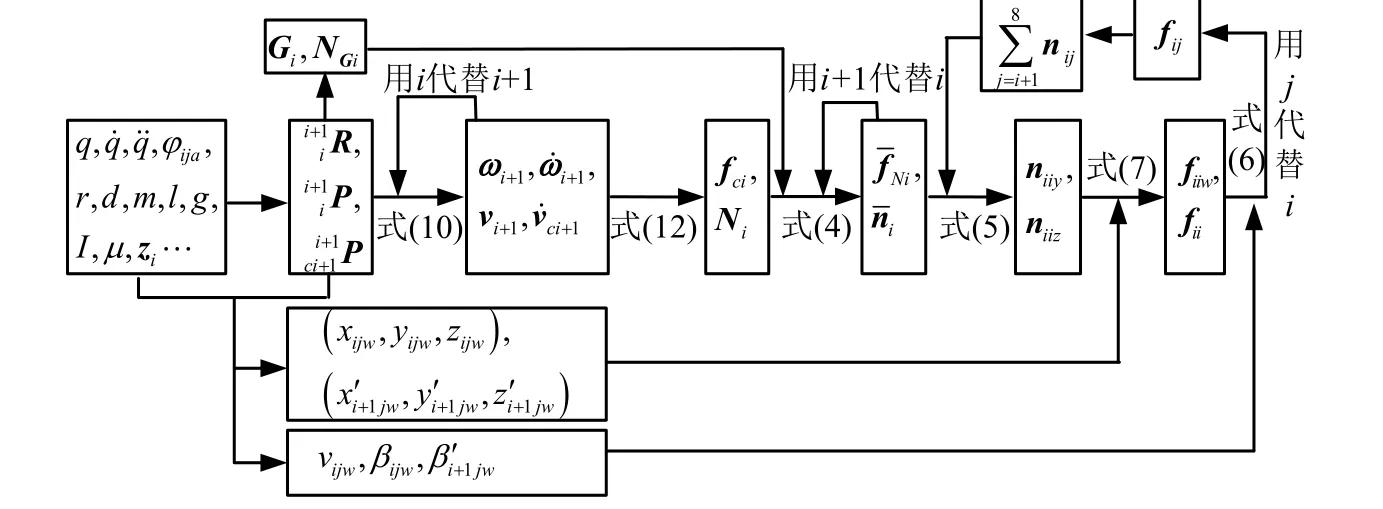
图5 准连续型机械臂各参数转化示意Fig.5 Schematic of Conversion of Parameters

2 动力学仿真

在建立动力学模型的基础上，借助Matlab 进行准连续型机械臂的动力学仿真分析，得出准连续型机械臂中24 根驱动绳的拉力大小与其运动状态的关系。图6 为准连续型机械臂的运动轨迹。为保证对应的轨迹规划下各臂杆的位置、速度及加速度变化曲线光滑且连续，令机械臂由水平状态开始，围绕x0轴线做圆周运动，0～3 s 由水平位置过渡到“画圆”的位置，3～15 s 每个臂杆的末端点围绕一个圆转动，15～18 s 由“画圆”的位置过渡到水平位置。

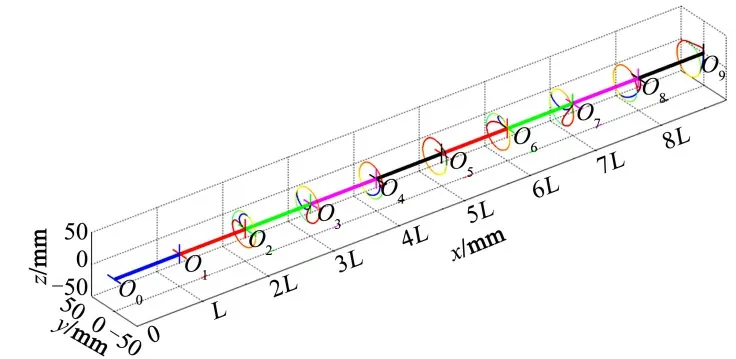
图6 准连续机械臂的运动轨迹Fig.6 The Trajectory of Manipulator

规定第i个臂杆的起始点为(xi，yi，zi)，坐标的变化规律如式（13）所示。其中T=8 s 为臂杆末端绕圆转一周的时间，采用七次多项式求解g(t)，得出式（14）。

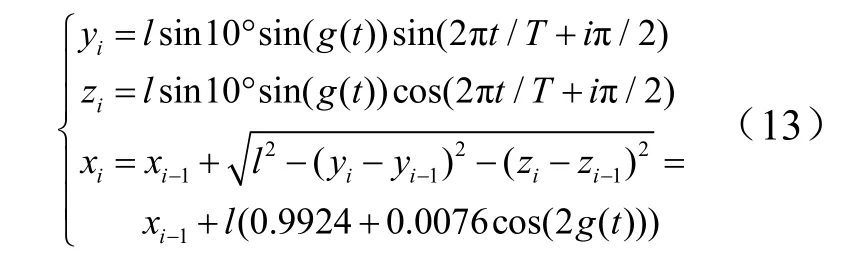
根据图6 对应的运动轨迹及前面建立的动力学模型，仿真可得8 个关节处的所有驱动绳的等效力矩在Yi轴、Zi轴方向上的分量大小niy、niz，如图7 所示。初始状态下等效力矩在Yi轴上的分量为niy(0)，从第1～8个关节分别为-64mgl、-49mgl、-36mgl、-25mgl、-16mgl、-9mgl、-4mgl、-1mgl（其中，m为臂杆的质量；g为重力加速度；l为臂杆的长度）。从图7 中可以看出当臂杆末端绕圆形轨迹转动一周时，等效力矩变化了 3个周期，等效力矩曲线光滑且连续。

图7 各个关节处的等效力矩变化Fig.7 Equivalent Torque Variation of Each Joint

3 非光滑时变最优化问题研究

通过动力学模型可推导出各个关节处所需的等效力矩，初始状态下在第i个关节处的所有驱动绳的等效力矩在Yi轴上的分量niy(0)=-(9-i)2mgl，进而可推出在第i个关节处的驱动第i个臂杆的驱动绳的等效力矩在Yi轴上的分量niiy(0)=(2i-17)mgl。如何将关节两个方向的力矩niiy、niiz转换为3 根驱动绳上的拉力尤为重要。

由2 个方程求解3 个未知量可有无穷解，首先建立对应的最优化问题的数学模型，如式（15）所示。

上述问题的目标函数J1(f)为变量fiia、fiib、fiic的线性函数，约束条件也为变量fiia、fiib、fiic的线性函数，可利用Matlab优化工具箱中的linprog函数求解该线性规划问题，通过仿真可得到24 根驱动绳拉力随时间的变化曲线，以驱动第3 个臂杆的绳子为例，3 根驱动绳拉力随时间的变化曲线如图8 所示。

图8 线性规划下的驱动绳拉力随时间的变化曲线Fig.8 The Variation Curve of the Tension of Driving Cables with Time under Linear Programming

从图8 中可以看出驱动绳拉力变化曲线连续但有些曲线不光滑、导数不连续，始终有1 根驱动绳的拉力约为零。若按照图8 中的变化规律控制驱动绳拉力，则容易拉断驱动绳，影响整个系统的运动平稳性。针对上述问题，将线性目标函数J1(f)改为如式（16）所示的非线性目标函数J2(f)，并设定了如式（17）所示的的fiia，fiib，fiic的下限。

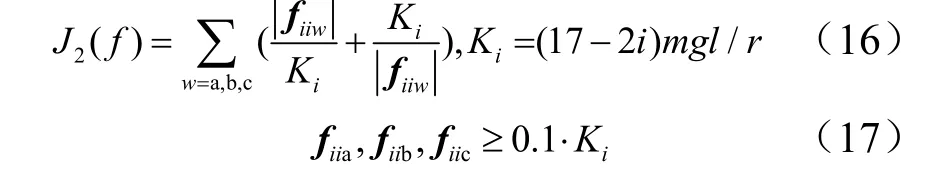
非线性规划问题的求解方法有许多种，本文分别采用遗传算法、模拟退火算法、粒子群算法、置信域算法进行非线性规划问题的求解，图9 为4 种算法下的驱动第3 个臂杆的3 根驱动绳拉力在9～10 s 的局部放大图。

图9 4 种算法下的驱动第3 个臂杆绳拉力的局部放大示意Fig.9 Local Enlarged View of the Tension of Cables Driving the Third Link under Four Algorithms

从图9 中可以看出，若利用前3 种算法进行最优化求解得到的曲线相对不光滑且计算时间较长，在某些地方容易陷入局部最小值，而且前3 种算法计算速度较慢且易出错，故不适用于计算24 根驱动绳拉力的实时期望数值。

故本文采用置信域算法进行求解非线性规划问题，可将计算时间大大缩短，通过仿真可得出24 根驱动绳拉力随时间的变化曲线，以驱动第3 个臂杆的3根驱动绳为例，其拉力变化曲线如图10 所示。

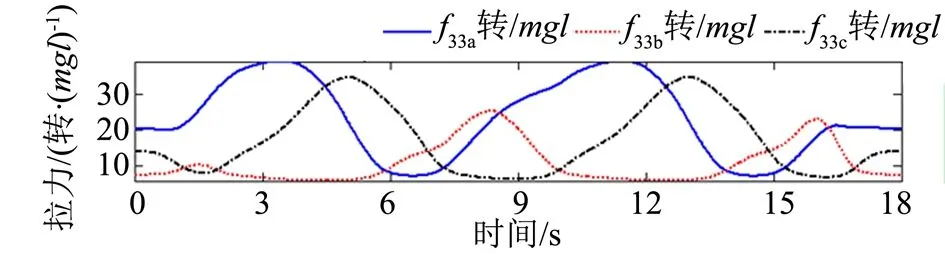
图10 非线性规划下的驱动绳拉力随时间的变化Fig.10 The Variation Curve of the Tension of Driving Cables with Time under Nonlinear Programming

分析仿真结果发现，任何时刻在第i个关节处驱动第i个臂杆的3 根驱动绳的拉力的等效力矩nii都等于本关节所有驱动绳的拉力的等效力矩ni减去驱动第i+1至第8 个臂杆的绳子在第i个关节处的等效合力矩，从而验证了动力学模型的正确性。

对比图8、图10，可以看出虽然线性规划下的驱动绳拉力的最大值（例如图8 中max(f33)=21.14mgl/r）小于非线性规划下的驱动绳拉力的最大值（例如图10 中max(f33)=38.93mgl/r），但非线性规划下的24 根驱动绳的拉力变化曲线连续且光滑，在机械臂的实时运动过程中，可提高整个系统的平稳性，有效地降低抖动。

该优化问题中含有3 个变量，为进一步降低计算量、减少计算时间，可利用式（7）中的两力矩niiy、niiz与3 根驱动绳拉力fiia、fiib、fiic的等式关系，将3 个变量转化为1 个变量，再采用置信域算法针对非线性目标函数求取最优解。最终得到的仿真结果与图10相同，但仿真时间从108 s 缩短至12 s，大大提高了两力矩与3 绳拉力之间的最优化转换速度。

4 结束语

本文利用牛顿欧拉法建立了准连续型机械臂的动力学模型，精准分析了运动过程中24 根驱动绳在不同位置的方向、速度，以及摩擦力对绳子拉力大小的影响，将每个关节处的驱动绳拉力及支持力两个未知量合并为一个未知量进行求解，从而实现了机械臂各参数之间的转化，并通过仿真验证了动力学模型的正确性。

同时针对关节力矩与驱动绳拉力之间的转换关系，提出了一种非线性目标函数，采用置信域算法消除了驱动绳拉力曲线的不光滑问题，提高了整个系统的平稳性，有效降低了抖动，并通过降元进一步缩减了计算时间，可满足准连续型机械臂的实时控制需求。

后续工作中将在本文建立的动力学模型的基础上，在准连续性机械臂的控制模型中增加驱动绳拉力的反馈信号，采用PID 或其他方法实时调节24 根驱动绳拉力，从而提高机械臂运动的平稳性及精确性。