弹载磁测系统等效安装误差的在线标定与补偿

张莺莺，张晓明,2，高丽珍,2，薛羽阳，刘 俊,2

(1.中北大学 电子测试技术国家重点实验室，太原 030051;2.中北大学 仪器科学与动态测试教育部重点实验室，太原 030051)

0 引言

随着现代战争向智能化、信息化方向的转变，常规弹药已经难以满足作战的要求。弹丸需要的不仅仅是足够的射程，而且需要更精准、更可控的远程攻击。因此，弹丸的制导化、信息化改造是常规弹药发展的必然趋势，也是当今世界精确制导武器发展的重要方向。弹丸制导首先需要得到弹丸准确的偏航、俯仰、滚转姿态信息，尤其对于旋转弹而言，由于弹体自旋不仅影响控制系统对尾翼的控制，同时也会带来俯仰、偏航的相互耦合。因此旋转弹药的制导化改造中，弹体滚转角参数的实时准确获取是弹药实现精确制导控制的前提条件。

在旋转弹姿态获取时常用的测姿系统有惯导测姿系统、地磁测姿系统[1]以及太阳敏感测姿系统。对于飞行过程高旋、发射条件高过载的旋转弹，MEMS惯导技术存在高过载性能退化、误差随时间累计的技术瓶颈以及初始对准的问题；太阳敏感测姿存在受天气气候影响较大的问题。另外还有卫星导航系统，它可以直接用于弹体导航，但是在高动态运动环境中需要经历较长时间的卫星信号捕获、跟踪，才能输出导航数据，且无法提供弹体的实时姿态角。因此旋转弹的制导化改造多利用地磁测姿系统进行弹丸姿态获取。通过弹载地磁传感器测量的地磁场矢量信息，实时解算出弹体的姿态滚转角。地磁测姿系统是建立在准确获取弹体任意时刻所处位置的地磁场矢量来确定弹丸的姿态信息的[2]，具有测量误差不累积、抗过载能力强、体积小、低成本等优势，已成为弹载导航测姿的主要测量方案之一[3]。但是地磁测姿系统也存在一些问题，在弹载磁测系统姿态解算过程中，滚转角实时解算精度受到磁传感器测量精度、磁传感器机械安装误差[4-5]以及弹体干扰磁场[6]因素的影响，其中磁传感器精度可通过事先标定进行补偿。而由于弹载磁矢量传感器芯片体积小，在硬件电路焊接中难于保证其敏感轴的方向，并且磁测系统与弹体轴间存在一定的装配误差，主要为机械安装误差角。另外在飞行过程中，弹体干扰磁场会随弹体在外弹道飞行中的工作状态变化，造成地磁信息的实际测量矢量与弹体坐标系不对准，表现为地磁信息不对准误差角。因此磁矢量传感器敏感轴与弹体坐标轴间存在磁场测量信息的机械安装误差和地磁信息不对准误差角，严重影响地磁测量滚转角的精度。度级的安装误差可导致滚转角解算十几度甚至几十度的测量误差。

在传统的安装误差标定方法中，主要有基于高精度无磁转台的多位置标定法[7-8]和基于三维椭球拟合的无基准标定法[9-12]。但这两种方法中主要标定磁场矢量测量单元与壳体的机械安装误差。该类方法整弹标定困难且均为事先标定，无法解决磁测信息的敏感轴和弹体坐标系轴不平行的弹载安装误差问题。方旭、王良明[13-14]等人分别提出了通过弹体特定的摆放位置来标定安装误差角的方法。该类方式操作简单，解决了整弹标定的问题，但同样仅适用于弹体发射前的机械安装误差标定，无法解决标定弹体飞行过程中由弹体干扰磁场引起的地磁信息不对准问题。另外由朱兴乐提出的通过放置另一标准磁传感器来矫正的方法[15]，对于小型的、体积要求严格的制导弹药而言并不适用。因此，需要一种可实时在线标定补偿地磁传感器等效安装误差的方法。

本文通过建立旋转弹体外弹道飞行中，地磁测量信息与弹体坐标系的等效误差角模型，提出一种基于类正弦信号特征的实时在线补偿磁测系统与弹体之间等效安装误差角的方法，以解决由磁测系统的敏感轴与弹体坐标系不平行带来的磁测系统测量弹体坐标系磁场信息不准确的问题。

1 旋转弹载环境地磁测量等效误差角模型

地磁测姿系统的解算弹体姿态角，其主要就是通过磁传感器测得弹体在任意时刻任意位置的三轴地磁场矢量信息，为测量系或弹体系下的地磁场矢量。当不存在误差时，弹体系与测量系重合。因此需要设立对应坐标系。

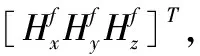
图1中弹体系b系到测量系m系中间存在安装误差角α，其旋转顺序按照“偏航-俯仰-滚转”的顺序旋转，即弹体系先绕Z轴转动偏航误差角αz到m1，再绕Y轴转动俯仰误差角αy到m2，最后绕X轴转动滚转误差角αx到m3，转动结果如图1所示。

图1 坐标系转换

Hb和Hf之间可由发射坐标系到弹体坐标系的转换矩阵关联。

(1)

b系是由f系转动滚转角γ得到，根据“前-右-下”的坐标系旋转规律，可得到转换矩阵如下：

(2)

其中:γ=ωt，则：

(3)

其中：

(4)

在飞行过程中受固定干扰磁场影响导致的磁测信息不对准误差，等效于磁传感器和弹体间存在安装误差角，因此设三轴地磁传感器的等效安装误差角为：

(5)

当按照“偏航-俯仰-滚转”的旋转顺序得到测量系下三分量时，由于等效安装误差角均为小角度，所以根据坐标系旋转关系简化后可得其对应的等效安装误差阵为：

(6)

即当存在等效安装误差时，最终测量的三轴矢量信息为包含误差信息的：

Hm=MinstallHb

(7)

将式(3)代入式(7)中可得磁测系统测量的包含误差项的弹体系三轴磁场矢量如式(8)：

(8)

将式(8)化简可得式(9)：

(9)

其中：

(10)

由式(9)可得，当磁测系统测量的磁矢量信息与弹体坐标系不平行时，机械安装误差角和干扰磁场带来的类安装误差角α，使得测量系下X、Y、Z三轴磁矢量信息分别出现类正弦波动和零偏。

根据式(9)将X、Y、Z轴磁矢量信息表达为：

(11)

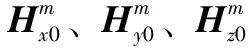
(12)

当Y轴磁场值出现峰值时，此时根据X轴测得的磁场值可得出：

(13)

即：

(14)

αx=tanθ2

(15)

2 误差补偿模型建立

根据以上分析可知，当磁矢量传感器与弹体坐标系之间存在等效安装误差角时，通过分析测量系下的三轴地磁矢量信息就可得到误差角。

最后根据式(6)得到等效误差阵Minstall。将后续测量系下的磁场值按照如式(15)进行误差补偿，可得到准确的弹体坐标系下地磁场三分量Hb。之后再利用标准弹体系磁场矢量Hb进行滚转角解算，即可得的弹体准确的滚转角，为旋转弹控制系统提供更准确的姿态滚转角。

(15)

3 实验验证

3.1 仿真验证

为验证模型的准确性，仿真生成一组弹体测量系下三轴磁矢量传感器测得的磁场值，即带有安装误差的磁场测量值。其中设置弹体运动的滚转角速率为5 r/s，系统采样频率为1 kHz，时间为5 s。同时设置弹轴坐标系下初始三分量Hf为[81234019712462]nT，加入的安装误差角为α=[5.4，-4.53，-6.11]°，仿真生成测量系下三分量后加入适当的测量噪声。得到磁场值如图3中X、Y、Z所示。之后根据上述等效安装误差模型进行误差角的解算及补偿得到误差补偿后的弹体系下磁场值：X1、Y1、Z1如图2所示。

图2 三轴磁场值

由图2的X、Y、Z可以看出当存在安装误差时，测得的弹体系三轴磁场存在零点偏移和波动幅值的变化。利用上述模型的方法补偿后，X轴波动幅值明显减小，Y、Z轴的零偏和波动赋值也进行了补偿。利用补偿前后的磁场值进行滚转角解算，与初始设置滚转角相比，得到补偿前后的滚转角解算误差如图3所示。

图3 补偿前后的滚转角误差

由图3可以看出等效安装误差补偿前，滚转角的解算误差最大值为8.64°，误差峰峰值为13.94°。可以看出5°左右的安装误差角对磁测系统滚转角解算精度影响在8°。通过分析三轴磁场信息，标定补偿等效安装误差角后解算的滚转角误差最大值为1.04°，误差峰峰值为1.41°。精度提高了8～10倍。满足旋转弹药制的导控制系统对滚转角精度的需求，同时验证了模型的准确性。

3.2 试验验证

模型验证后，进一步进行物理试验验证。本实验采用霍尼韦尔公司生产的HMC1053芯片作为磁敏感单元，ST公司生产的stm32f405rgt6为处理单元。根据上述模型的计算方式将等效安装误差角的在线标定补偿方法移植到下位机中。

由模型可知，该误差角在线标定补偿方法需要磁测单元至少滚转一周，得出三轴磁场峰峰值，进而得出交流、直流分量，之后才能计算出误差角。因此，在线标定过程中，第一圈的滚转角误差与未补偿前解算的滚转角误差相同。将系统安装在高精度三轴飞行仿真转台上进行在线误差角标定补偿验证。

在高精度飞行仿真转台上，以转台反馈的滚转角为标准；地磁测姿系统解算输出的滚转角为在线标定补偿后的滚转角；系统输出的原始电压值解算的滚转角为未补偿的滚转角，得到滚转角及滚转角误差如图4、图5所示。

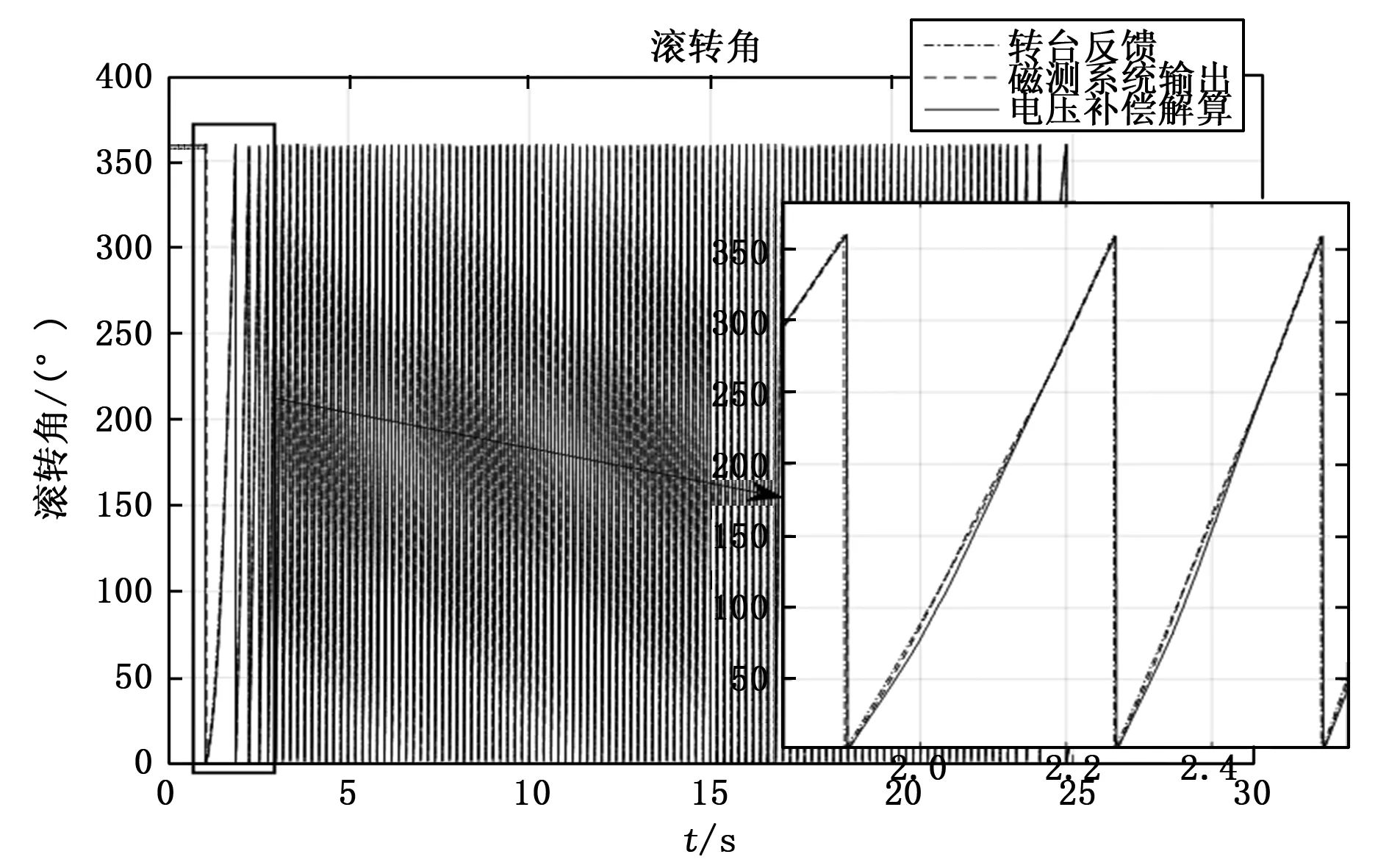
图4 仿真转台验证滚转角

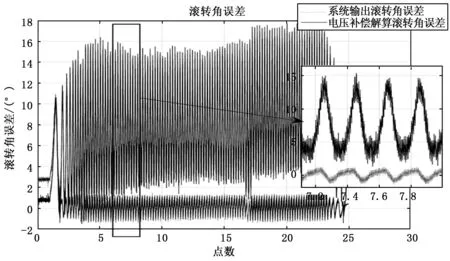
图5 仿真转台验证滚转角误差

由图4、图5可以得出，在三轴飞行仿真转台上，第一转补偿前后解算的滚转角相同，与转台反馈的滚转角相比误差较大，这是因为第一转正在进行误差角的标定。一转之后进行在线误差角补偿，补偿后的滚转角解算误差最大值为1.5°，误差峰峰值为2.92°。直接用电压值补偿未补偿等效安装误差解算得到的滚转角误差最大值为17.87°，误差峰峰值为18.38°。在线标定补偿比未补偿误差解算的滚转角精度提高了6倍以上，极大提高了滚转角的解算精度。并且补偿后滚转角解算误差在2°以内，可以满足旋转弹等制导弹药对滚转角精度的需求。

4 结束语

通过分析三轴磁场信号，建立三轴磁矢量信息与等效安装误差角的模型，根据类正弦信号特征实时标定补偿磁矢量传感器的等效安装误差角。从而解决测量系下三轴磁矢量与弹体系地磁矢量不平行的问题，最终提高滚转角解算精度。试验结果表明，5°左右的等效安装误差角可带来十几度的滚转角误差峰峰值，说明等效安装误差对滚转角解算的精度影响较大。而经过该方法标定补偿后，相比与未补偿等效安装误差解算的滚转角，利用该方法补偿后，滚转角解算精度可提高6倍以上，解算误差保持在2°以内，满足旋转弹制导弹药对滚转角的精度需求。