基于双环永磁体结构的多稳态能量采集器建模及性能分析

周振华，易正旸，陈书涵，李战慧，刘 鑫

（1.长沙理工大学汽车与机械工程学院，长沙410114；

2. 湖南科技大学机械设备健康维护湖南省重点实验室，湖南湘潭411201；3. 机械装备高性能智能制造关键技术湖南省重点实验室，长沙410114）

近年来，无线传感器网络技术和物联网技术正处于高速发展时期。然而绝大多数无线传感器节点目前仍使用电池供电，如果无线传感器节点数量众多或者布置在危险区域，一旦电池耗尽，更换电池将需要庞大的费用[1]。为了解决无线传感器节点持续供电的难题，能量采集技术成为研究热点[2]。典型的环境能量来源有太阳能、热能、振动能等[3–4]，而振动能被认为是最好的环境能量来源。

振动能量采集的主要研究方向为扩展能量采集的带宽。目前拓展能量采集带宽的方法主要有线性拓频和非线性拓频两种方法[5]。在线性拓频方面，张梦倩等[6]在压电悬臂梁外部串联电感，通过改变电感来改变系统的固有频率。非线性拓频又可分为非线性单稳态拓频和非线性双稳态拓频，非线性单稳态拓频是利用非线性力学特性，使振动能量采集系统的频响曲线向低频或高频弯曲，以拓宽系统响应的带宽[7–9]。但是非线性单稳态能量采集器无法采集更低频的振动能量。而非线性双稳态拓频可以解决这一问题。Cottone 等[10]提出了基于磁斥力的非线性双稳态能量采集器，通过将矩形永磁体固定在倒立摆的自由端，同时在其正对面放置一块同极永磁体提供磁斥力。实验结果表明：合理永磁体间距下，系统呈现双稳态。双稳态能够显著提高采集器的输出功率和带宽。Ertuck 等[11]也提出了类似的结构，采集器由铁磁压电梁和两个固定永磁体组成，两固定永磁体对称分布在压电梁附近，利用磁吸力产生双稳态特性，研究结果表明双稳态采集器相较于线性采集器具有更宽的响应带宽和更大的输出电压。此后双稳态能量采集领域出现大量研究成果：吴子英等[12]提出了一种附加非线性振子的双稳态能量采集器，并对系统的基谐波和超谐波响应进行了研究，但是该结构较为复杂，不利于集成化；李海涛等[13]提出了一种压电电磁复合式双稳态能量采集器，其特点在于可以同时采集压电片和线圈中的能量；Deng等[14]提出了一种具有新型波纹管结构的双稳态能量采集器，相较于悬臂梁结构的采集器，波纹管应力分布更加合理，结构也更加紧凑；Zhou等[15]提出了一种柔性双稳态能量采集器，通过添加带磁铁的柔性梁结构来降低势垒高度，但是其柔性梁也存在位移，因此不利于集成化。

本文提出了一种基于双环永磁体结构的多稳态能量采集器，其结构紧凑，可以通过改变外环永磁体的结构参数改变能量采集器的势能曲线。建立了该多稳态振动能量采集器的非线性力学模型，分析外环永磁体参数对势能曲线的影响规律，通过数值仿真研究分析三稳态和双稳态状态下系统的动态响应、电压输出特性和吸振性能，结果表明三稳态状态下的能量采集器能在更宽的频率范围内产生更大的能量输出以及有更好的吸振作用。

1 能量采集器的结构与建模

1.1 能量采集器的结构

本文所提出的具有双环永磁体结构的多稳态能量采集器结构如图1所示。其结构主要分为振动部分、发电部分和支撑部分。振动部分由线性弹簧、片簧、内环永磁体和外环永磁体组成，线性弹簧和片簧为系统提供线性刚度，内环永磁体和外环永磁体为系统提供非线性刚度。发电部分由发电永磁体和发电线圈组成，发电永磁体在发电线圈内做往复运动，使线圈内部发生磁通量变化产生感应电动势，从而实现能量采集。支撑部分由铝制支架、片簧和工作点调节装置构成，铝制支架起主要支撑作用，片簧可以约束振子的振动方向，工作点调节装置可以调整内环永磁体的垂直位置，以抵消重力对装置的影响。

图1 双环永磁体结构的多稳态能量采集器结构及其平面图

1.2 双环永磁体的非线性磁力建模

双环永磁体的结构参数如图2所示。其中外环永磁体的外半径为rout,内半径为rin，高度为h；内环永磁体的外半径为rout2，内半径为rin2，高度为b。za为内环永磁体与外环永磁体中心的垂直位移。J为永磁体的剩余磁通密度，μ0为真空磁导率。

图2 同轴双环永磁体的结构参数

为了获得多稳态能量采集器的特性，需要计算双环永磁体间的磁力。

根据文献[16]，双环永磁体间的轴向磁力可由式(1)至式(4)求得：

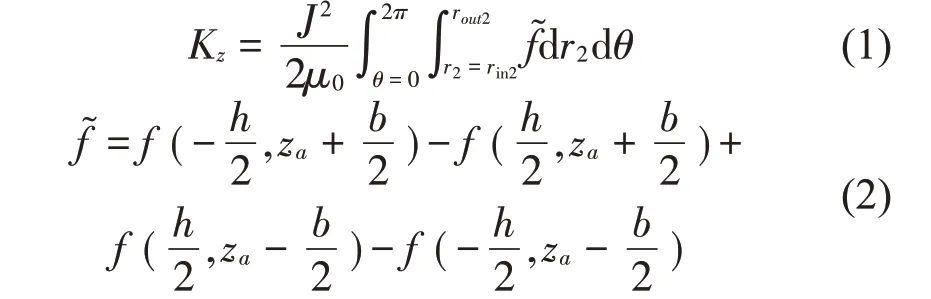
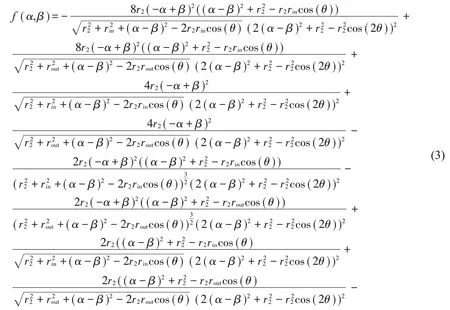
其中：r2为内环永磁体的积分半径范围，θ为内环永磁体的积分角度范围。如表1所示。

表1 双环永磁体参数

磁力计算的参数如表1所示。通过式(3)求解出各个f(α, β)，再通过式(2)求出函数f，并将其代入式(1)中求出轴向磁刚度Kz，并对轴向磁刚度Kz进行积分得到轴向磁斥力Fz。

为了验证磁力的解析表达式，采用COMSOL有限元软件进行仿真，双环永磁体的有限元建模如图3所示。求解结果与数值仿真对比如图4所示。可以看出根据有限元法得到的磁力和根据数值解析法得到的磁力基本吻合，证实了磁力数值解析表达式的正确性。

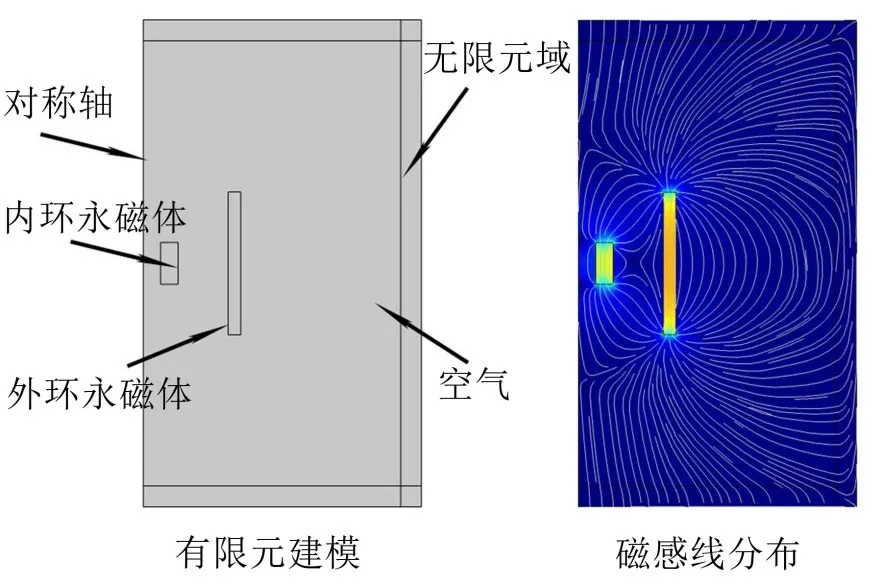
图3 双环永磁体的有限元建模和磁感线分布

图4 同轴双环永磁体间的磁力

2 外环永磁体结构参数对势能曲线的影响规律

根据参考文献[17]，双环永磁体间的非线性刚度可用如下多项式拟合得到：

其中：n0、n2、n4为非线性刚度的多项式系数。非线性磁力的表达式可由式(5)积分得到：

其中：k1、k3、k5为非线性磁力的多项式系数。

能量采集器的势能函数可由环形永磁体间的磁势能和线性弹簧的弹性势能相加得到，系统总势能函数表达式如下：

其中：k为线性刚度。

2.1 外环永磁体内半径对势能曲线的影响规律

考虑到能量采集器的体积约束，设定外环永磁体rout=14 mm。并令k=200 N/m，内环永磁体的参数：rout2=5 mm，rin2=2.5 mm，b=6 mm不变，研究外环永磁体参数对势能曲线的影响规律。

为了研究外环永磁体内半径对势能曲线的影响，设定外环永磁体高度h=12 mm，外环永磁体内半径rin的变化范围为11 mm～13.5 mm。系数(k+k1)随外环永磁体内半径rin的变化规律如图5 所示。采用最小二乘法进行拟合，拟合多项式表示为

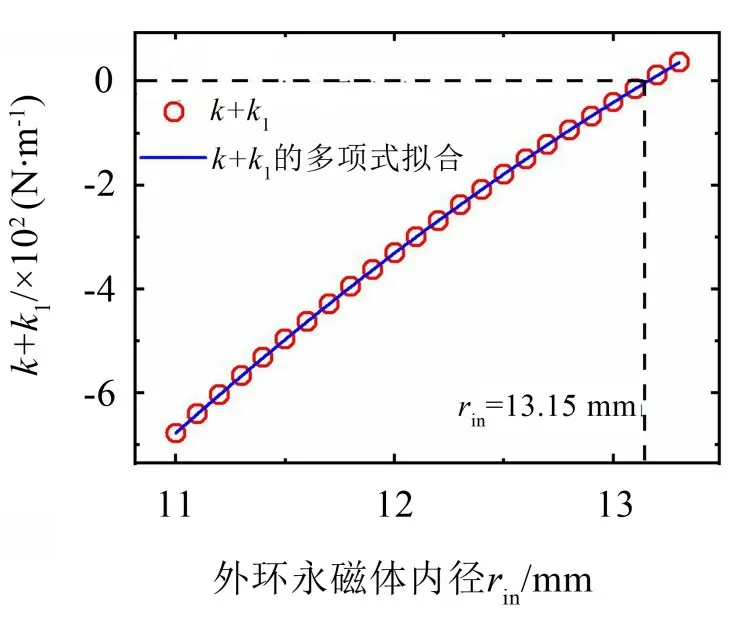
图5 (k+k1)随外环永磁体内半径的变化规律曲线

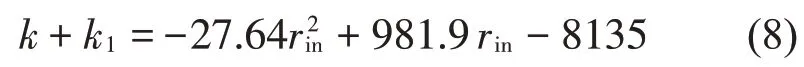
显然，结合方程式(8)可知，当外环永磁体内半径rin=13.15 mm时，k+k1=0，此时能量采集器的总体线性刚度为0，呈现近零刚度特性。结合图6所示的不同外环永磁体内半径下的势能曲线可知，当rin<13.15 mm时，k+k1<0，能量采集器线性刚度为负，此时能量采集器为双稳态，势能曲线有一个势垒和两个势阱，且随着rin增大，双稳态的势垒高度和势阱间距都在减小；当rin>13.15 mm 时，k+k1>0，此时能量采集器变为单稳态，势能曲线只有一个势阱。

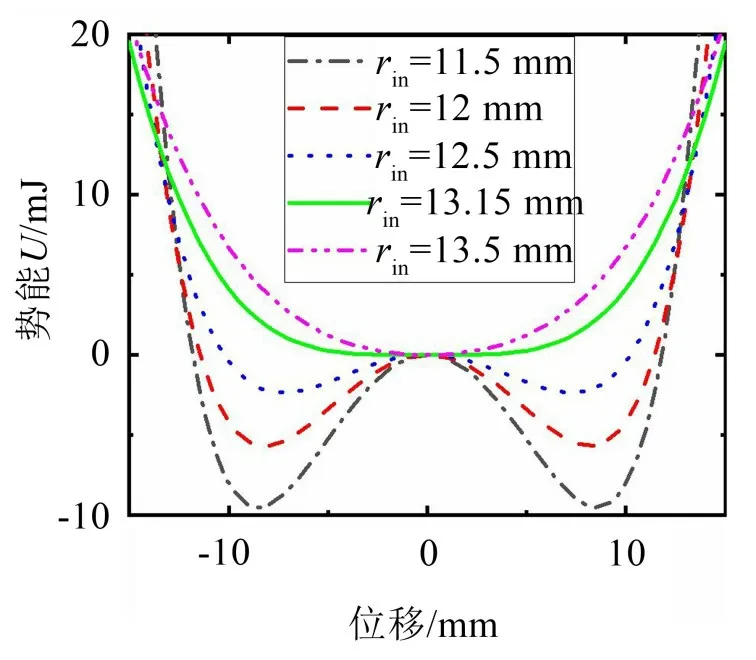
图6 不同外环内半径下的势能曲线

基于上述分析结果可知：减小外环永磁体内半径会使能量采集器由单稳态变为双稳态，但过小的外环永磁体内半径会使势垒高度过大，导致振子无法越过势垒，因此确定合适的外环永磁体内半径是设计能量采集器的基础。

2.2 外环永磁体高度对势能曲线的影响规律

为了研究外环永磁体高度对势能曲线的影响，设定外环永磁体内半径rin=12.2 mm，外环永磁体高度h变化范围为12 mm～22 mm，系数(k+k1)随外环永磁体高度h的变化规律如图7 所示。其拟合多项式表示为

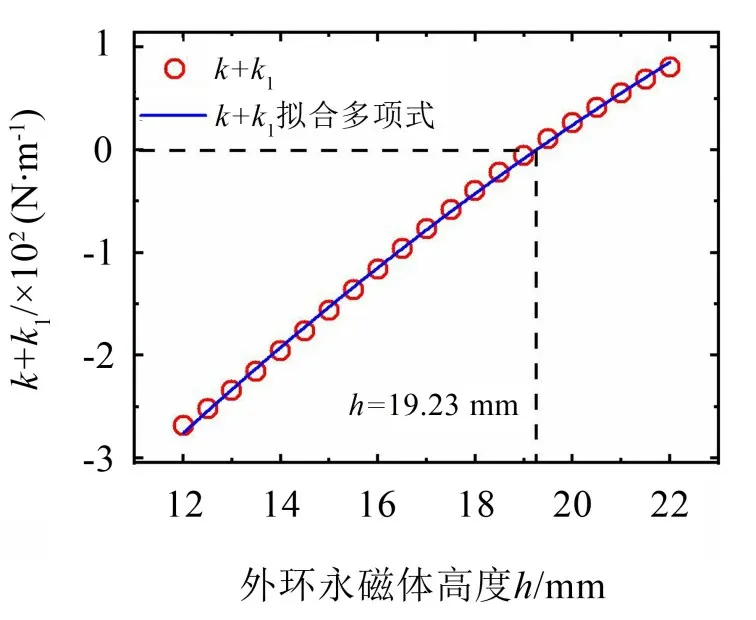
图7 (k+k1)随外环永磁体高度的变化规律曲线

结合方程式(9)可知当外环永磁体高度h=19.23 mm 时，一次项系数k+k1=0。结合图8 所示的不同外环永磁体高度下的势能曲线可知，当外环永磁体高度h<19.23 mm 时，k+k1<0，能量采集器总体线性刚度为负，势能曲线有两个势阱，为双稳态系统。且随着h的增大，势垒高度降低，势阱间距增加；当外环永磁体高度h>19.23 mm 时，k+k1>0，能量采集器总体线性刚度为正，此时系统有3 个势阱。

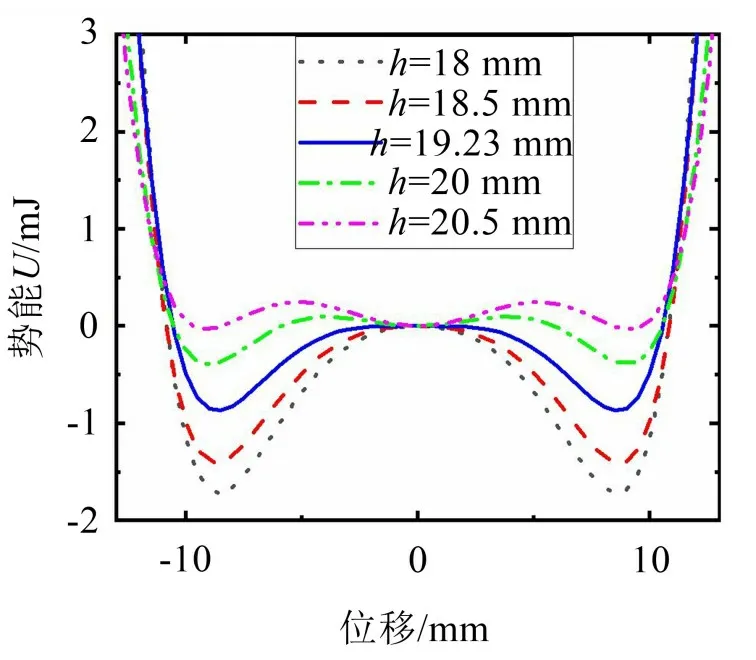
图8 不同外环永磁体高度下的势能曲线

基于上述分析结果，在确定外环永磁体内半径之后，通过调整外环永磁体的高度可以在一定范围内在减小势垒高度的同时增大势阱间的间距，并且随着外环永磁体高度的增加，当一次项系数k+k1>0 时，系统将变为三稳态状态。三稳态状态下的能量采集器势垒高度更低，势阱间距更大，振子更容易通过势垒且振动位移更大，这意味着三稳态能量采集器能在更宽的频率范围内产生更高的能量输出。

3 谐波激励下的动态响应及电压输出特性分析

本节研究激励频率和激励幅值的变化对双环永磁体结构能量采集器的影响。选取图8中外环永磁体高度h=20.5 mm(三稳态)和h=18 mm (双稳态)两组外环永磁体进行对比。能量采集器的机电耦合方程可以表示为

其中：m为振子质量，c为机械阻尼，k为线性刚度，为激励加速度，ξ为机电耦合系数，L为发电线圈电感，R为外部负载电阻的阻值，z为振子位移。能量采集器的系统参数如表2所示。通过龙格库塔法对方程式(10)进行求解。

表2 能量采集器参数

谐波激励的加速度为

其中：ω为角频率，A为激励幅值。输出电压的有效值为

其中：u为t时刻的瞬时电压。

3.1 不同激励频率下的动态响应及电压输出特性分析

由于0.01 Hz～20 Hz的振动被称作低频超低频振动，因此选取数值仿真的频率范围为0.01 Hz～20 Hz。选取激励加速度幅值A=8 m/s2进行三稳态和双稳态状态下的能量采集电压对比。图9 为A=8 m/s2时的输出电压对比。当f=0.01 Hz 时，两者几乎均无电压输出。

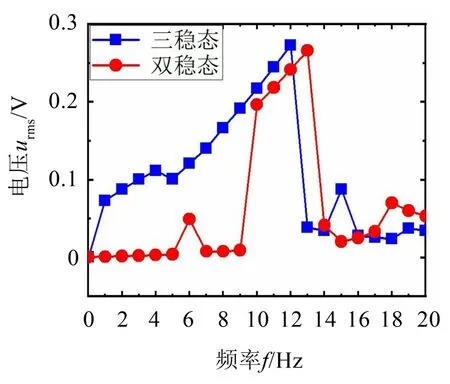
图9 A=8 m/s2时不同激励频率下的输出电压的有效值对比

当f=1 Hz 时，双稳态状态下的能量采集器几乎没有输出电压，而三稳态状态下的能量采集器则有了一定的电压输出。当f=10 Hz 时，双稳态状态下的能量采集器的输出电压才开始迅速提升。随着激励频率继续增加，振子无法越过势垒，电压反而降低。因此，三稳态状态下的能量采集器带宽为1 Hz～12 Hz，双稳态状态下能量采集器带宽为10 Hz～13 Hz。

仿真结果表明在相同激励加速度幅值的情况下，三稳态状态下的能量采集器相较于双稳态状态下的能量采集器拥有更低的工作频率和更宽的带宽。

3.2 不同激励加速度幅值下的动态响应及电压输出特性分析

设定外界的激励频率为f=8 Hz，激励加速度幅值变化范围为1 m/s2～12 m/s2。三稳态和双稳态状态下的能量采集器在不同激励加速度幅值下的输出电压对比如图10 所示。三稳态状态下的能量采集器在A=4 m/s2时达到激励加速度阈值，输出电压迅速增大。而双稳态状态下的能量采集器则需要达到A=9 m/s2时才能达到激励加速度阈值。

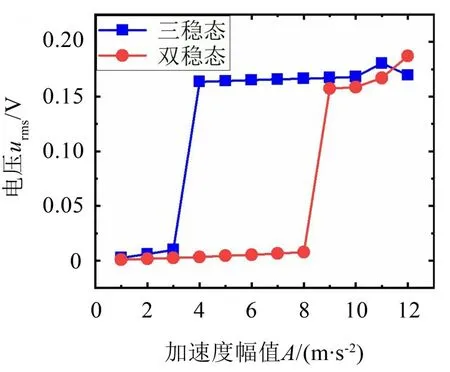
图10 f =8 Hz时不同激励加速度幅值下的输出电压对比

仿真结果说明三稳态状态下的能量采集器可以在更低的激励加速度幅值下获得更大的能量输出。

4 多稳态能量采集器吸振性能分析

本文提出的多稳态结构不仅能够提升能量采集性能，同时也能作为吸振器吸收振动，由线性主振系系统和多稳态吸振器构成的模型如图11 所示。其中M为主振系质量，k′为主振系刚度，c′为主振系阻尼，主振系上部为多稳态吸振器。z′为主振系的位移。

由图11 结合式(10)可以写出吸振系统的微分方程：

图11 吸振系统模型

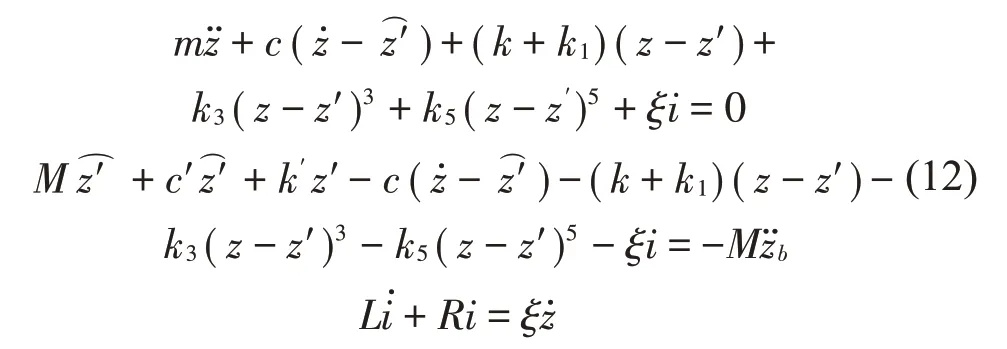
设定主振系质量M=1 kg，刚度k′=2 000 N/m，阻尼c′=0.3 Ns/m，其他参数如表2所示。令主振系初始位移为10 mm，并添加均值为0、标准差为8 m/s2的白噪声进行激励，观察不同稳态下的吸振效果。图12(a)为5 s～15 s主振系振动时域曲线，从图中可以看出三稳态吸振效果明显好于单稳态和双稳态。图12(b)为主振系振动频域曲线，在共振频率处，三稳态吸振下的主振系幅值比单稳态吸振低37.4%，比双稳态吸振低29.4%。图13(a)为吸振器振动时域曲线，可以看出在5 s～14 s 时三稳态吸振器依然进行大幅周期运动，而双稳态吸振器则由于势垒较高，在7.5 s时从大幅周期运动衰减成了阱内小幅周期运动，因此三稳态采集器能够吸收主振系大量的振动能量，这也是其吸振效果最优的原因。图13(b)为吸振器振动频域曲线，尽管在共振频率处三稳态吸振器幅值低于单稳态吸振器，但是其在其他频率上都有着较高的振动幅值。

图12 主振系振动时频曲线

图13 吸振器振动时频曲线

5 结语

所提出的基于双环永磁体结构的多稳态能量采集器不仅可以拓展能量采集的带宽，而且相对于悬臂梁式的能量采集器，双环永磁体结构更加紧凑，更有利于集成化。充分研究了外环永磁体的高度和内径对势能曲线的影响规律，研究发现：随着外环永磁体高度增加，能量采集器由双稳态转变为三稳态。并通过数值仿真计算和对比了三稳态状态下的能量采集器和双稳态状态下的能量采集器在不同激励频率和激励幅值下的动态响应和输出电压。结果表明相对于双稳态状态下的能量采集器，三稳态状态下的能量采集器在低频具有更小的能量阈值，更容易越过势垒，能够在较宽的低频范围内采集能量。最后分析对比了不同稳态的能量采集器对振动抑制的影响，能量采集装置处于三稳态状态时吸振性能最好。