基于LQR的车体与车下设备耦合振动控制及共振效应研究

雒耀祥，缪炳荣，陈翔宇，彭齐明，蒋钏应

（西南交通大学牵引动力国家重点实验室，成都610031）

高速列车车体轻量化的设计原则在实现车体质量减轻、运行能耗降低的同时，也不可避免使得车体的动态性能恶化。其主要原因一方面是车体刚度下降，另一方面是运行速度的提高使得随机不平顺激扰的频域加宽，更容易激发车体的垂弯模态。其中车体1阶垂弯频率正好位于人体感受敏感的频率范围内，会使旅客乘坐舒适性会出现不同程度的恶化[1]。而车体刚度不足，使得车辆在运行过程中容易发生共振。所激发的共振可能会使车体与设备之间的连接处发生局部的颤振，从而造成车辆零部件的松动或者容易产生疲劳破坏[2]。为尽可能降低上述不利影响，需采取相应的减振和隔振措施对车体振动进行抑制。

文献[1，3–7]分析了车下设备吊挂参数对车体弹性振动的影响，并对合理的参数匹配给出建议。这些研究是从DVA(Dynamic vibration absorber)理论出发，属于车体弹性振动抑制的被动方法。被动方法的不足在于设计参数难以满足不同的复杂工况。为此，有必要从振动控制的角度来对其进行补充研究。

曾京和罗仁[8]在模型中考虑半主动开关减振器，分析其对车体振动的影响。Zheng[9]将主动二系悬挂和结构阻尼相结合，同时对车体的刚性和弹性振动进行抑制。曹辉等[10]提出改善垂向平稳性的鲁棒控制方法。以上文献虽然对车体弹性振动抑制从控制角度进行了研究，但缺少对车体与车下设备耦合振动的考虑。

Foo[11]考虑车下设备的影响及作动器的动力学特征，利用主动悬挂抑制车体的弹性振动。汪群生等[12]利用LQR(Linear quadratic regulator)最优控制理论对车体与车下设备的耦合振动进行半主动控制。另外，文献[13–15]中利用LQR对四分之一车辆模型进行振动控制，但并未考虑结构弹性振动模态的影响及耦合振动的作用。

基于对以上相关文献的分析，本文利用LQR方法对车体与车下设备之间的耦合振动进行控制。针对以上文献研究中的不足，在进行振动控制时，不仅应用优化算法来决定控制参数的取值，而且还考虑了不同目标函数的设置对控制效果的影响。

1 理论背景

1.1 欧拉-伯努利梁理论

为考虑车体的弹性振动，可将其视作两端自由的均质等截面Euler梁。考虑图1所示的简化模型，设梁的垂向位移为w(x,t)，则其振动方程可表示为[16]

图1 简化的Euler-Bernoulli梁模型

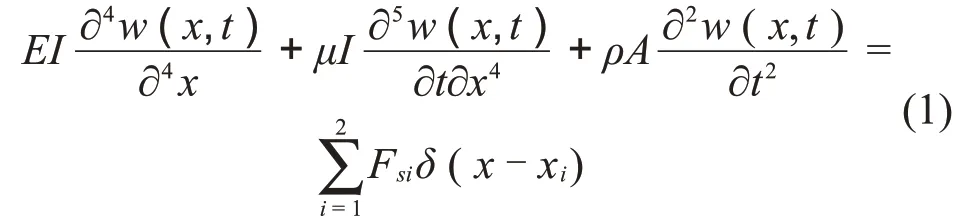
其中：EI是车体等效抗弯刚度，μI是内滞阻尼系数。

设第m阶弹性振动的模态坐标为qm(t)，对应的振型函数为Ym(x)。利用振型叠加法截取前N阶弹性振动模态并考虑车体刚性的沉浮z(t)和点头θc(t)振动，则车体的振动位移可表示为

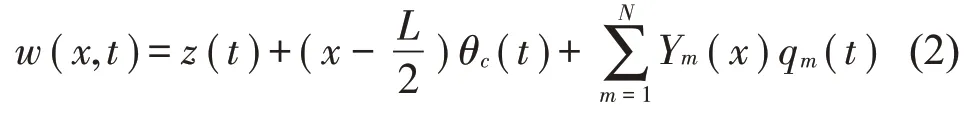
将式(2)代入到偏微分方程式(1)中，可得：

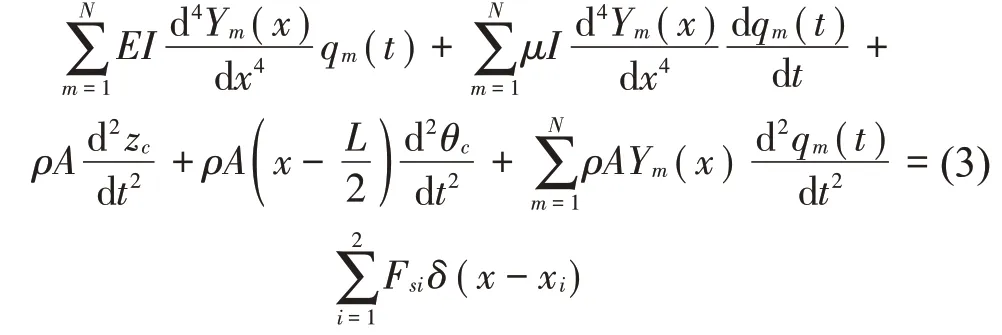
将式（3）左右两边同乘以Yn(x)dx，并沿车体长度进行积分，可得车体弹性振动的微分方程为

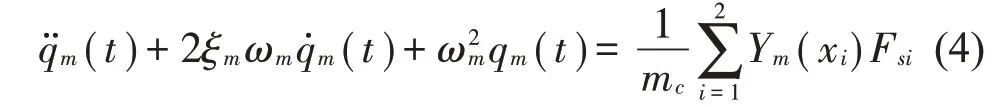
在式(4)中[16]：

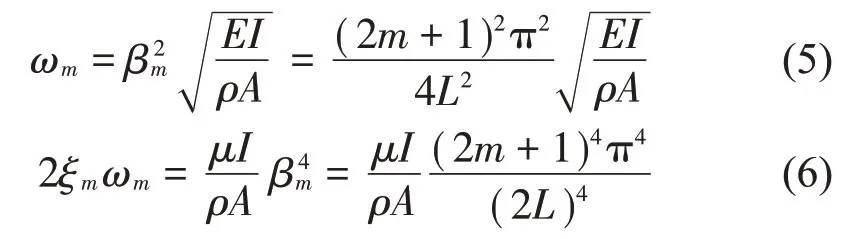
1.2 轮轨接触理论

根据Hertz非线性接触理论，轮轨间的垂向动态作用力可表示为[17]

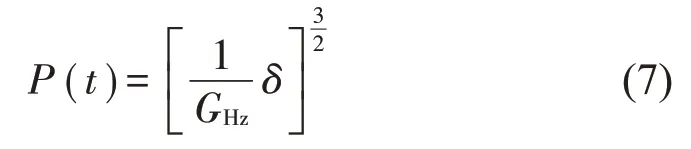
其中：GHz是Hertz接触常数，δ是轮轨间弹性压缩量。

轮轨间的弹性压缩量δ包括轮轨间的静压量δ0和相对位移δjwr(t)两部分。当δ<0 时轮轨发生脱离，可认为轮轨力为0。所以轮轨垂向力可表示为[17]

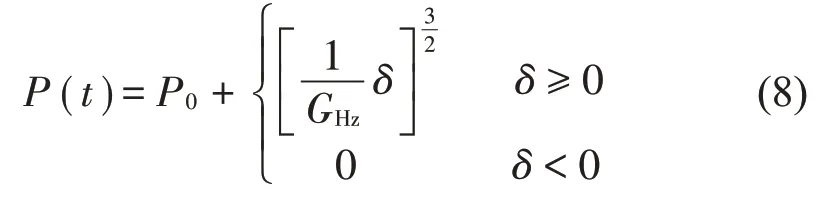
利用以上方法求解轮轨垂向力时，由于轮轨间的非线性关系，在求解过程中须采用较小的时间步长。为此，可采用线性化的接触刚度，其可由式(9)求得：

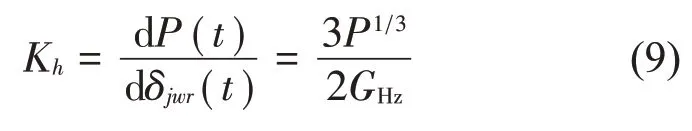
1.3 振动控制技术

LQR线性二次型控制是最优控制中的一种经典算法，其控制规律简单并且具有非线性容限较令人满意的优点，在振动控制中具有广泛的应用。假设有线性时不变系统的状态空间方程为

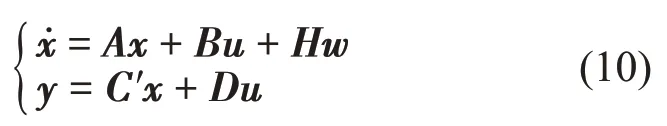
引入最优控制的性能指标[18]：

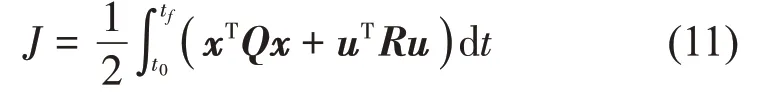
其中：Q和R表示加权矩阵。由线性二次型最优控制理论可知，要使J最小，所输入的控制信号应为[18]

其中：P是对称矩阵，满足以下的Riccati代数方程[18]：

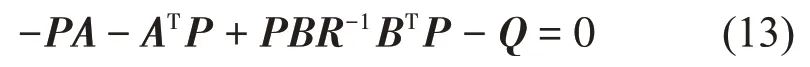
2 建模及控制参数求解

2.1 动力学建模

考虑图2所示的垂向简化模型，整个系统包括1个车体、2个转向架、4个轮对和1个车下设备。除对车体额外考虑前3 阶弹性振动外，其余部件均视为刚体。整个系统共15个自由度，主要参数列于表1。

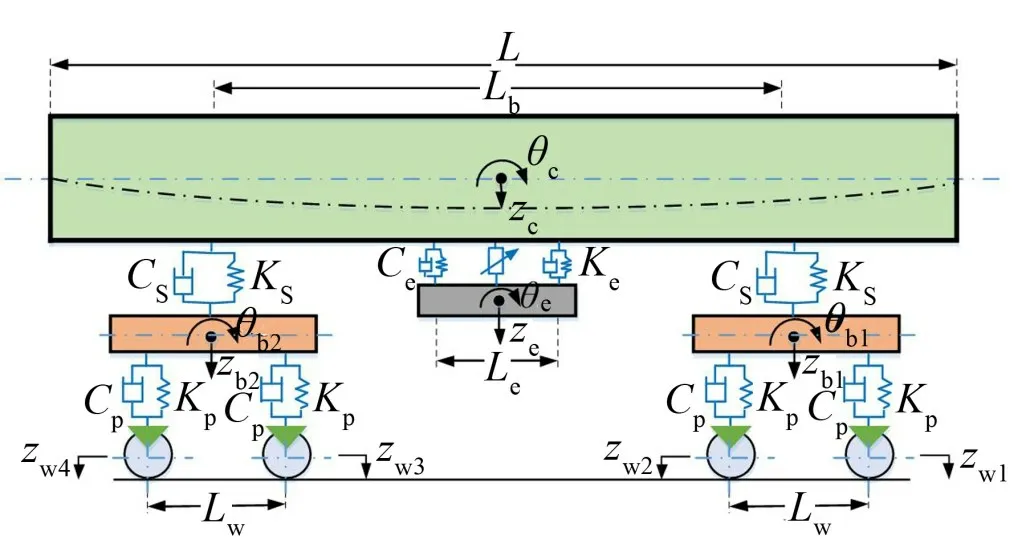
图2 简化整车垂向模型

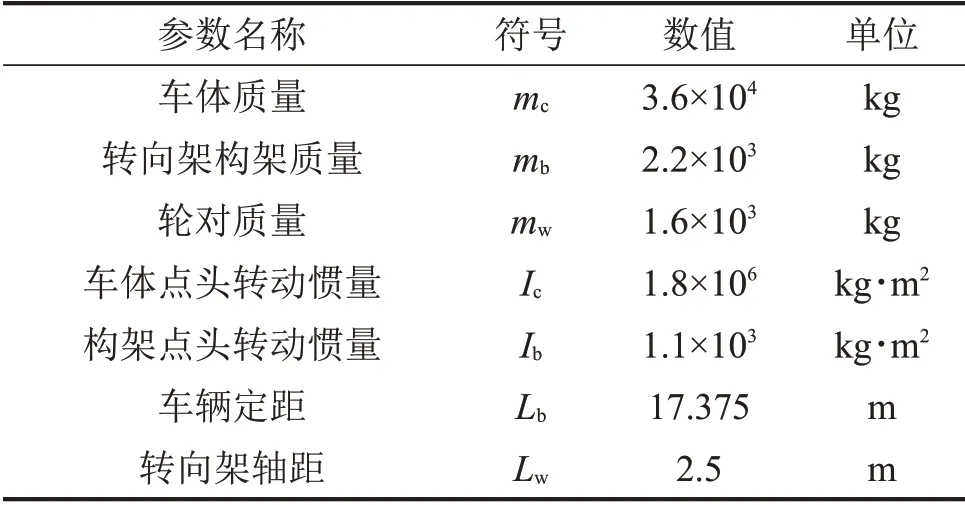
表1 车辆数值模型部分参数

记Fsi和Fej分别为二系悬挂和车下设备悬挂元件对车体的作用力，Fu为输入的控制力，则可得考虑车体刚柔耦合振动的系统运动方程为

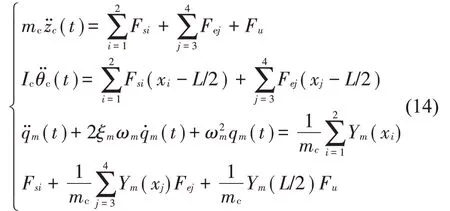
车下设备的运动方程为

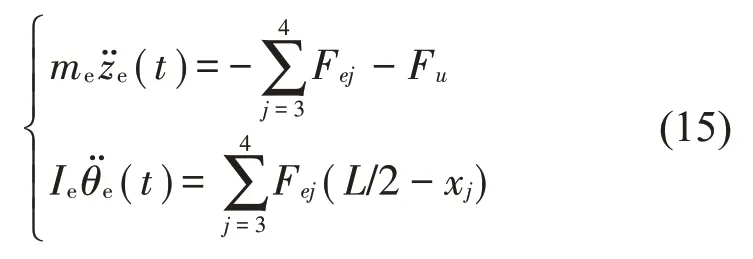
记Fpn是一系悬挂对第n个轮对的作用力，可得转向架构架的的运动方程：

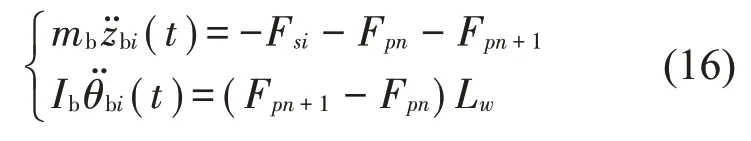
其中，当i=1时，n=1，当i=2时，n=3。

结合之前所说明的轮轨垂向力计算方法，可得：

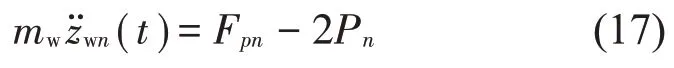
至此，已得到系统的运动微分方程组，可将其整理成式(10)所示的状态空间方程的形式。则A为30×30 阶系统状态变量矩阵；B为30×1 阶控制力输入矩阵；H为30×4 维的激励输入矩阵；C′和D的矩阵维数由实际所需的输出数目所决定。

2.2 模型验证

为了对以上所建立的高速列车整车垂向动力学模型进行验证，建立各部件自由度更为完善并且考虑非线性轮轨接触的三维刚柔耦合模型如图3所示。

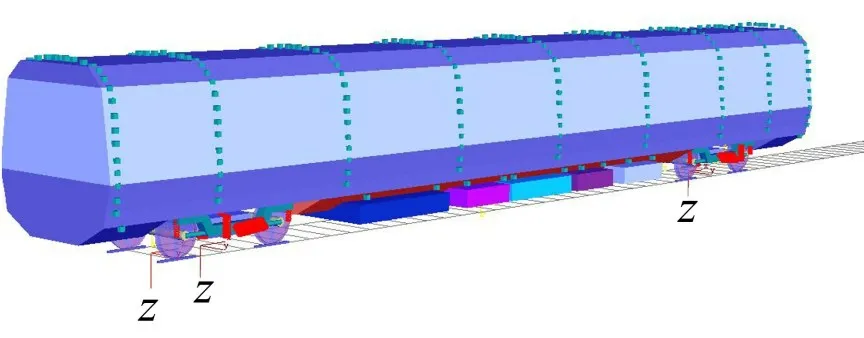
图3 多体动力学模型

对简化垂向模型和多体动力学模型添加实测武广线垂向轨道不平顺激励，计算车体中间位置处的垂向振动加速度及功率谱密度见图4。

从图4(a)中可以看出，简化模型与MBS(Multibody system)模型的时域仿真结果存在较小的差异。对图4(a)中的最大值及RMS 值进行统计，结果列于表2。从中可以看出，建立的垂向简化模型能较好地反映车体的振动特性。

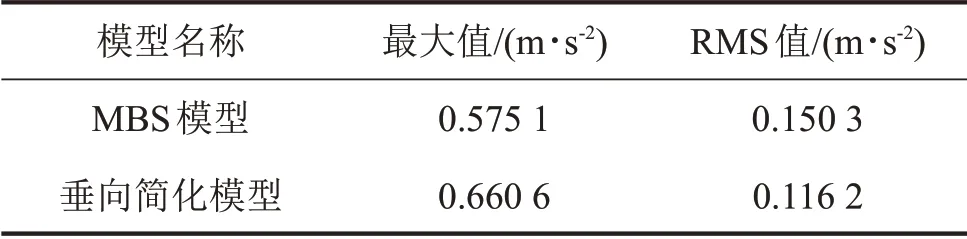
表2 精细模型与简化模型部分结果对比

从图4(b)的对比中可以发现：在所研究的频率范围内，简化模型不仅存在与MBS 模型近似的主频，而且还能较好地反映振动能量的变化趋势。因此，可以将建立的垂向简化模型用于后续的研究中。

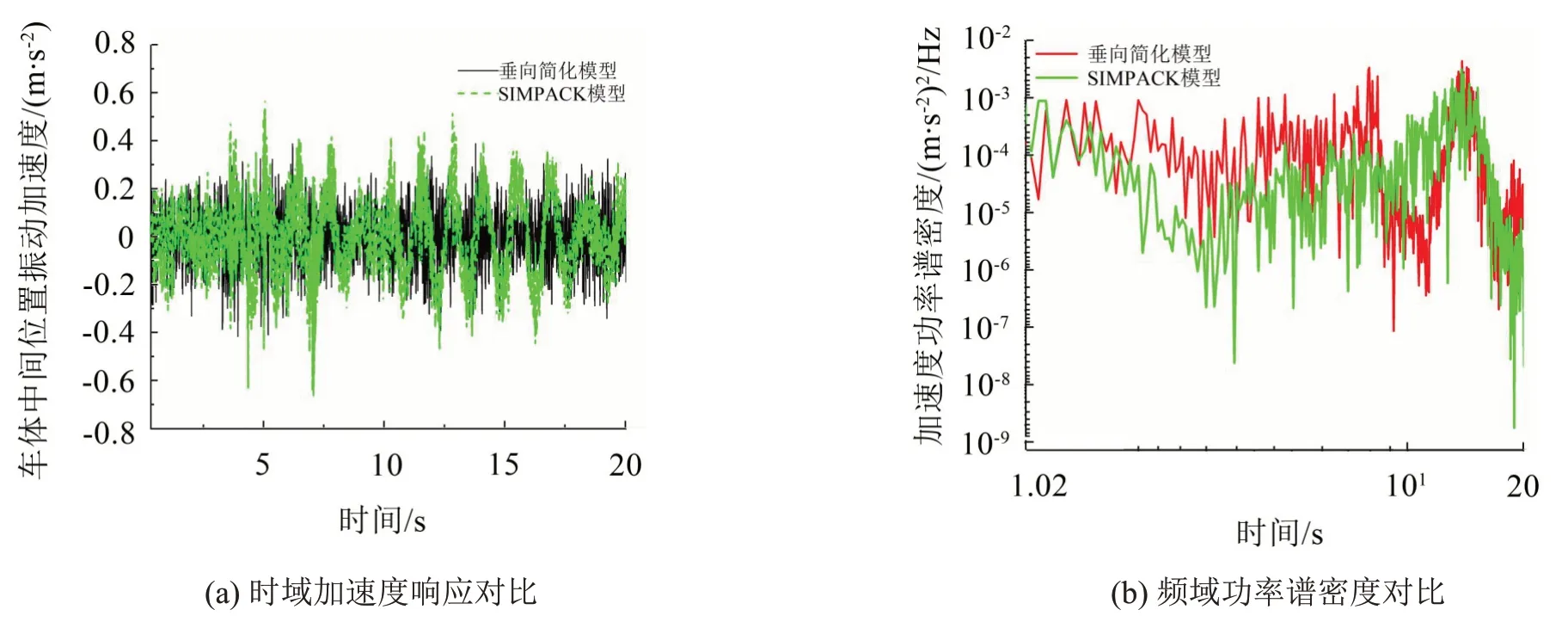
图4 不同模型计算结果比较

2.3 车体与车下设备耦合共振频率确定

对垂向模型施加同步正弦激扰，图5所示是3种情况下车体中间位置处的动力放大系数。

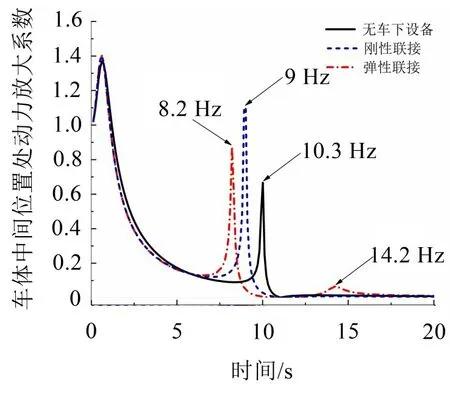
图5 车体中间位置处振动位移的动力放大系数

可以看出，车下设备刚性悬挂时，车体1阶垂弯频率下降到10 Hz 以下。而车下设备弹性悬挂时，车体与车下设备发生耦合振动，对应的动力放大系数由单峰值变为双峰值，其中低阶耦合共振频率为8.2 Hz。

另外，从图5可以看出，将车下设备弹性悬挂于车体时，能够降低车体的弹性振动。文献[4–5]中也指出要减小车体振动的传递率可通过降低车下设备悬挂刚度的方式来实现。但注意到过多地降低车下设备悬挂刚度，会使挠度增加，可能会引起车下设备与其它部件之间的干涉，这在文献[19]中也有所考虑。因此，利用车下设备弹性悬挂的方式对振动进行抑制时，为尽量避免这一矛盾，可通过施加控制来作为抑制车体弹性振动的一种补充方法。

2.4 同步激励下车体振动最优控制

为了对车体的弹性振动进行抑制，选择占弹性振动分量较大的1 阶垂弯振动为控制目标。为此，构造如下的适应度函数：

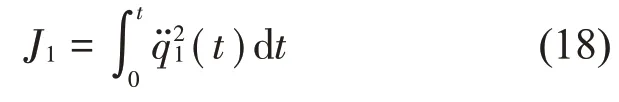
根据LQR控制中权重矩阵的选择规则，可取定R为单位阵、Q为对角阵。为使上式所表达的适应度函数达到最小，利用全局寻优能力强的基因遗传算法对Q中各元素进行参数寻优。根据图5 的结果，取频率为8.2 Hz 的同步正弦激励作为输入，寻优过程如图6所示。

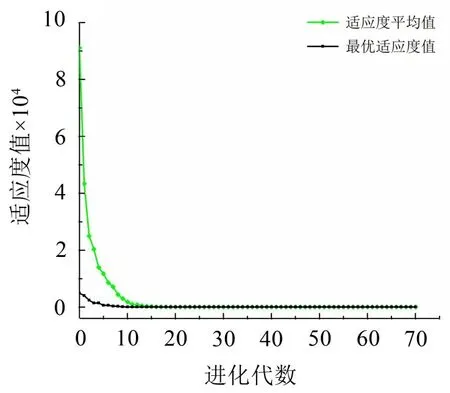
图6 同步正弦激扰下的寻优过程

可以看出，进化20代左右时，寻优过程收敛，最优解基本不变并保持在稳定值。

2.5 轨道不平顺激励下车体振动控制

考虑车辆实际运行中所受随机轨道不平顺的作用，对车体振动进行最优控制。由于短波对动力学的影响比较大，因此考虑激扰波长的范围为0.5 m～80 m。利用文献[20]中的方法，通过反演得到德国低干扰谱高低不平顺的样本。用该样本做为输入，结合遗传算法进行全局参数寻优。图7所示为寻优过程，可以看出寻优过程最后收敛于稳定值，基本保持不变。

图7 随机激扰下的寻优过程

3 结果分析与讨论

3.1 同步激励下控制结果讨论

基于图6的寻优结果，最优控制前、后车体振动加速度及功率谱密度的对比分别见图8和图9。

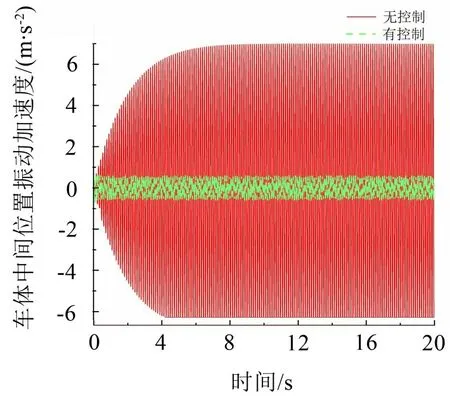
图8 控制前、后车体振动加速度响应

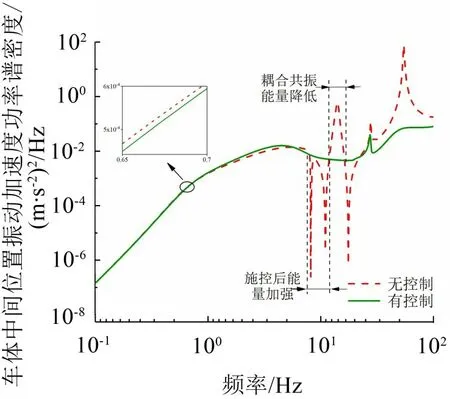
图9 控制前、后车体振动加速度功率谱密度

从图8 可以发现，在控制后车体振动加速度明显减小。进一步计算可得，未控时车体中间位置加速度RMS 值为4.590 2 m/s2，而施控后该值降低为0.413 6 m/s2。这说明所得结果可以很好地抑制车体与车下设备的耦合共振。从图9 中可以看出，施加最优控制后，仅在车体与设备耦合共振频率附近振动能量降低，但在其他影响乘坐舒适性的频段内振动能量加强。

3.2 轨道不平顺激励下控制结果讨论

利用图7的优化结果，计算控制前、后车体振动加速度与功率谱密度分别见图10 和图11。在轨道不平顺激励下，未控时车体加速度RMS值为0.127 7 m/s2。而施控后RMS 值变为0.063 2 m/s2，相比于未控制前下降50%。

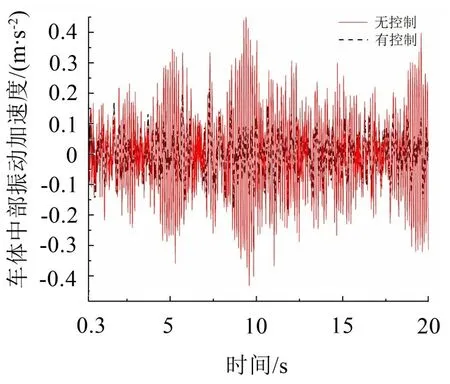
图10 控制前、后车体振动加速度响应

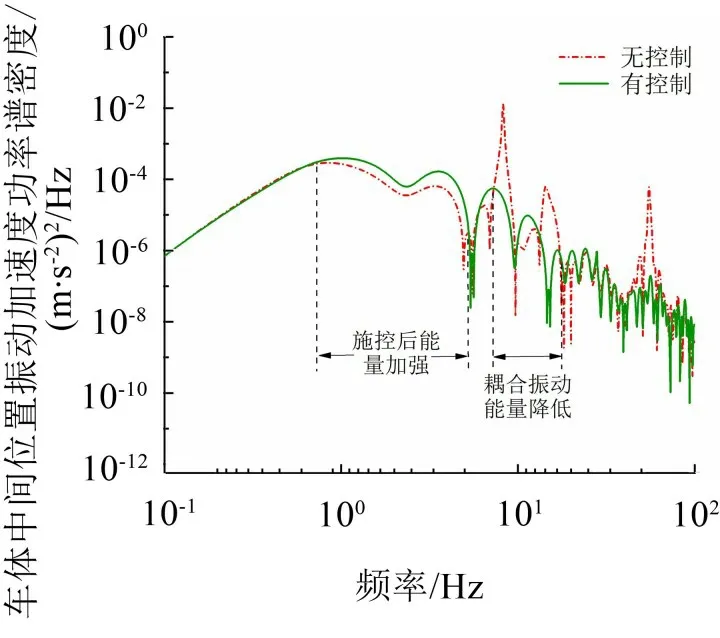
图11 控制前、后车体振动加速度功率谱密度

从图11 中可以得到和之前同步激励下类似的结果，在耦合共振频率的附近车体的振动能量显著降低，但在其他人体较为敏感的频段内却有振动能量的加强。这不利于乘坐舒适性的改善，有必要进一步对这一问题寻求解决方案。

3.3 频率性能优化

由于车体刚柔耦合振动的原因，以上控制效果存在只能在较窄的频率范围内发挥减振效果的不足。为此，在以以上时域性能为目标的基础上，进一步引入频域性能对控制参数进行优化。

构建以频域性能指标为目标函数如式(19)所示，分别在同步正弦和延迟随机激扰下进行优化。

式中：S(ω)表示输入激扰的功率谱，HS(ω)→am是从输入激扰到车体中间位置振动加速度的传递函数。

图12(a)至图12(c)和图12(d)至图12(f)分别为同步正弦和延迟随机激扰下的优化结果。从图12 的时域结果可以看出，以频域性能指标为目标进行参数优化，同样能达到降低车体振动加速度幅值的目的。对频域结果进行分析可以发现，其不仅能在车体与设备耦合共振的峰值频率处起到振动抑制的效果，而且也能在人体较为敏感的较宽频段内起到较好的减振效果。尤其是在低频段和对舒适性影响较大的频段内，振动能量降低较为明显，有利于乘坐舒适性和运行平稳性的改善。

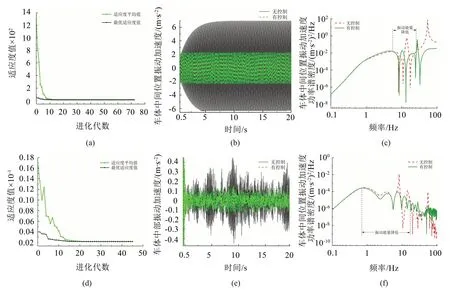
图12 以频率性能为目标所得优化控制结果

3.4 与其它控制方法的效果比较

为进一步说明方法的可行性及优势，利用文献[21–22]中经过参数优化并具有良好效果的模糊控制做为比较对象。构建图13(a)所示的模糊系统，控制参数优化过程如图13(b)。利用优化结果进行模糊控制，并与上一小节中LQR 控制效果进行对比，结果见图13(c)。可以看出，本文所用方法对车体的振动抑制效果明显比模糊控制好。这说明本文所用控制方法及提出基于频率性能为目标的参数设定方法在抑制车体与车下设备耦合振动时，具有一定的优势。

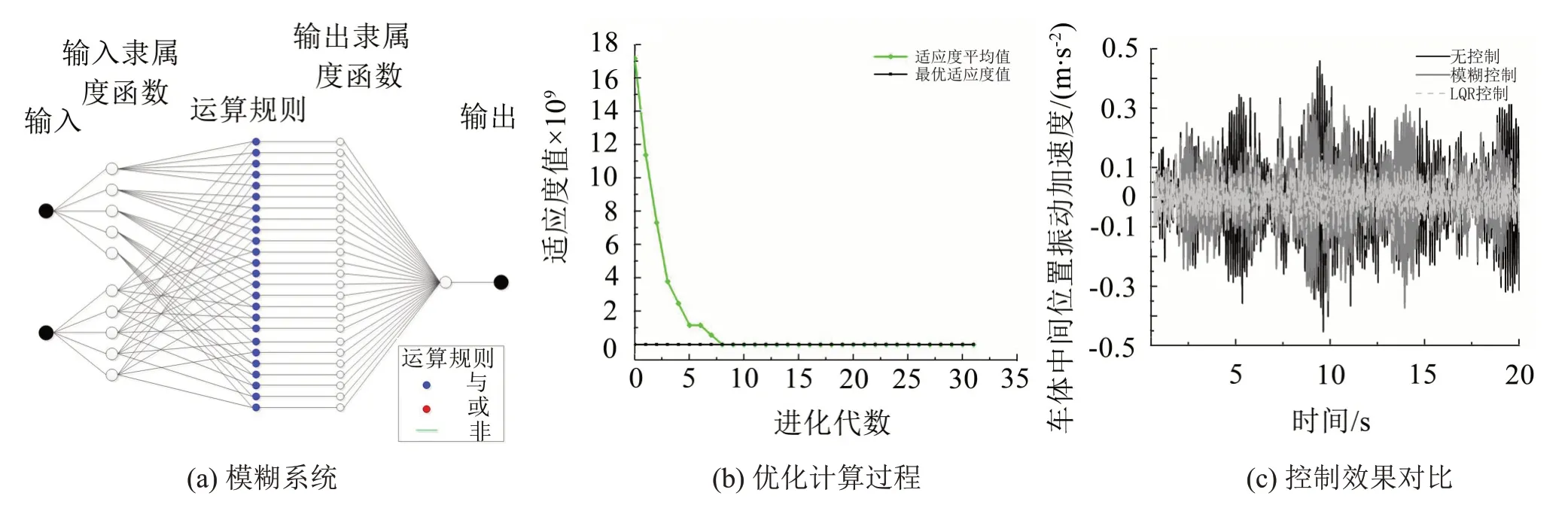
图13 模糊控制系统及控制效果

3.5 参数扰动对控制效果的影响

考虑到所用的控制方法为最优控制，其在工况变化时应具有一定的控制“裕量”。为此，考量车体质量变化和轨道激扰恶化对控制效果的影响，前者用来模拟载客量发生变化的工况，而后者则用来模拟轨道条件变差的情形。表3所列是车体质量变化情形下，控制前、后车体加速度RMS 值的变化。可以看出，车体质量变化对控制效果的影响不是很大，在所研究的参数范围内，最优控制仍能保持较好的控制效果，使车体加速度RMS值的降幅保持在40%以上。

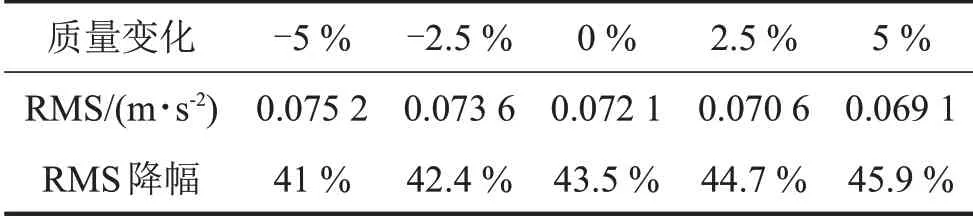
表3 车体质量变化引起车体振动加速度RMS的变化

在随机激扰样本中添加一定的随机噪声用来模拟轨道激扰的恶化，表4 所列是车体加速度RMS 值的降幅。可以看出，随着噪声的增加，车体加速度RMS 值有一定程度的增加。但相比于未控时的RMS 值0.127 7 m/s2，轨道激扰增加2%的随机噪声时，控制结果仍能保持RMS值11.7%的降幅。说明所得控制参数在轨道激扰恶化时能保持一定的控制“裕量”。

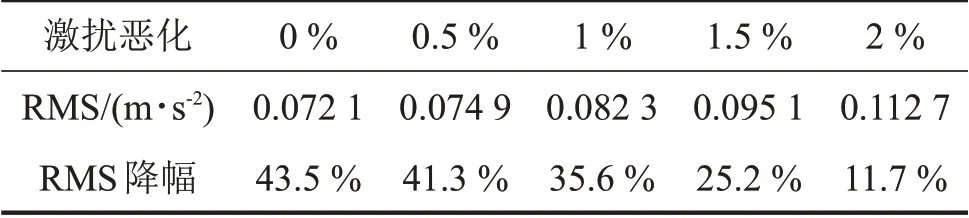
表4 轨道激扰变化引起车体振动加速度RMS的变化

4 结 语

通过以上的研究，所得主要结论有：

(1)对车下吊挂设备采用刚性悬挂会使车体一阶垂弯振动的固有频率有所下降，从而恶化车体的振动。而将车下设备弹性悬挂时，会使车体放大系数表现出双峰值，并在峰值频率处出现车体与车下设备的耦合共振，求得低阶耦合共振的频率为8.2 Hz。

(2)比较将车体时、频域性能分别作为优化目标所得的控制效果，结果表明，以频率性能为目标所得的控制参数，不仅能显著降低车体加速度幅值，而且还能在较宽频段内降低振动能量，尤其是在低频段和对乘坐舒适性影响较大的频段内减振效果较为明显，因此有利于相应性能的提高和改善。

(3)车体质量在±5%的范围内变化时，其对最优控制效果的影响不是很大。车体加速度RMS 值的降幅基本都保持在40%以上。最优控制参数对随机不平顺激扰比较敏感。但在随机激扰中增加不超过2%的随机噪声时，仍能保持一定的控制“裕量”，车体加速度RMS 值相比于未控制时仍有10%以上的降低。