材料与几何参数对薄膜超材料吸声性能的影响

王家声，刘 艳，李秋彤，陈亚楠

（1.上海理工大学机械工程学院，上海200093；2.上海材料研究所，上海200437；3.上海消能减震工程技术研究中心，上海200437）

声学超材料是一种新型人工材料，通过对其在亚波长尺度下的结构设计，可实现对低频宽带声波的高效调控，获得天然材料所不具备的超低频吸声能力，为众多工程领域的低频降噪问题开辟了新的技术路径[1–3]。其中，薄膜声学超材料的质量轻、体积小，可广泛应用于多种轻量化应用场景[4–6]。很多研究学者针对其隔声性能做了大量研究，分析了胞元的结构参数、薄膜密度及泊松比等材料参数对其隔声性能的影响[7–9]，还通过优化其几何设计提高隔声性能[10–12]；此外，又提出了多种主动控制方法用于调节薄膜声学超材料的隔声性能[13–15]。随着薄膜声学超材料研究的不断深入，其吸声性能也受到极大关注。Mei 等[16]提出了采用两块半圆形附加质量对称分布在矩形薄膜两侧的薄膜声学超材料，首次发现了其低频的吸声特性；Chen 等[17]研究该薄膜声学超材料的吸声性能，发现了随着附加质量个数的增加，吸收峰数目也逐渐增多；张忠刚等[18]研究附加质量厚度对其吸声性能的影响；Zhu等[19]利用穿孔板与弹性薄膜组合成双自由度的谐振吸声系统，发现了此结构会在低频范围内出现两个吸收峰，间接扩大了低频声波的吸收带宽；Ma等[20]提出在原有薄膜下部增加一个密封空气层，通过调节空气层厚度，可改变吸收峰频率特征；刘怡然等[21]将吸声薄膜声学超材料与亥姆霍兹共鸣腔结合，发现调节薄膜张力与厚度可改变吸收峰值频率。

现有对于薄膜声学超材料的吸声性能研究，大多通过改变附加质量厚度与数目、调整附加质量布设位置、构建复合结构等方式，提高其吸声性能，重点关注第一吸收峰的频率特征以及频带宽度，鲜有分析材料参数（泊松比、密度、弹性模量等）与几何参数（半圆形半径、薄膜长度）对其吸声性能的影响，特别是薄膜的材料与几何参数。为此，本文基于弹性波动理论，初步分析吸声型薄膜超材料低频吸声性能的产生机理；随后联合有限元及边界元法，建立声固耦合模型，并通过常规吸声系数实验对模型进行验证，探究吸收峰的出现原因及其幅频特性；针对材料几何参数不同的薄膜声学超材料，研究材料几何参数对吸收峰幅频特征的影响，为拓展吸收带宽、优化薄膜声学超材料的吸声性能奠定了基础，同时提供了具有规律性的参考依据，对噪声控制的多场景应用具有重要的理论指导意义。

1 弹性波动理论

薄膜声学超材料是一类由薄膜、附加质量和框架构成的亚波长结构，按降噪原理，分为吸声型和隔声型两大类，本文主要研究吸声型薄膜声学超材料（后文简称“薄膜声学超材料”）。类比于弹簧振子，附加质量可视为振子小球，薄膜可视为振动弹簧。当入射声波垂直入射时，考虑薄膜受张力的微变形作用，薄膜的振动微分方程可表示为[22]

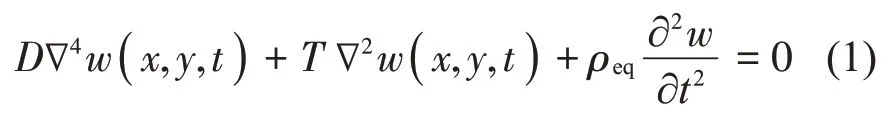
式中：T为薄膜张力；ρeq为等效面密度；w(x,y,t)为薄膜表面任一点(x,y)在t时刻的垂向位移；p0为声压幅值。假设入射波为平面波，则薄膜垂向位移w(x,y,t)可表示为关于时间t的函数：

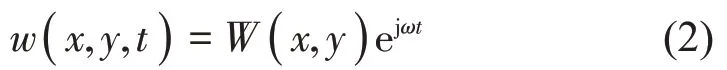
式中：W(x,y)为薄膜振动的主振型。去掉时间相关项，即可得到薄膜结构的振动特征方程：

式中：k为波数，k=ω/c；ω为平面波角频率；c为空气中声速，c2=T/ρeq。将式(3)按照模态叠加理论进行求解，利用模态函数的正交性得：

式中：Mm为薄膜面密度矩阵，Ms为附加质量的质量矩阵，KT为薄膜张力刚度矩阵。由式(4)可得薄膜声学超材料的1阶固有频率：

当入射声波与这一吸声结构发生共振时，会引起薄膜和附加质量剧烈振动，大部分声能量转化为薄膜的弹性应变能，使其具有“吸声”能力。采用能量法计算薄膜的总弹性应变能U，即[23]：

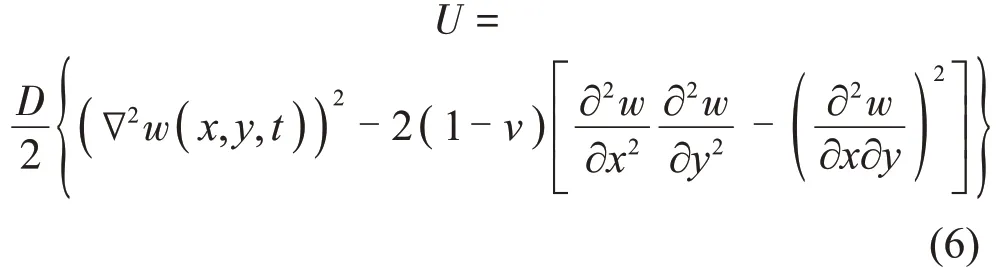
式中：D为薄膜的抗弯刚度，D=Eh3/12(1-ν2)；h为薄膜的厚度；E为薄膜的弹性模量；ν为泊松比。若薄膜表面某一区域垂向位移w的1阶偏导不连续，则2阶偏导将会发散。基于式(6)预测，当薄膜声学超材料的局域共振状态被激发时，薄膜与附加质量连接区域的振动速度不连续，则共振频率附近狭长区域薄膜声学超材料的总弹性应变能显著增大。根据能量守恒定律，薄膜系统损耗能量(包含透射能量)可表达为

式中：E1为薄膜损耗模量，V为薄膜体积。忽略透射能量，吸声系数可定义为

式中：P为入射声波能量密度。由式(8)可知，吸声系数与薄膜的总弹性应变能呈正相关，薄膜声学超材料的吸声性能主要来源于薄膜的弹性应变。

2 薄膜声学超材料仿真计算

2.1 声固耦合模型

以Yang 等[24]提出的吸声型薄膜声学超材料为研究对象，其胞元几何结构如图1 所示。由外部框架、薄膜和附加质量3部分构成。其中，薄膜采用聚乙烯材料，四周用铝合金框架固定，并对其附加2.2×105Pa 的张力；附加质量为两块对称放置的半圆形铁块（半径为6 mm、厚度为1 mm），两铁块圆心之间相距15 mm；各部分材料参数如表1所示。

表1 吸声型薄膜声学超材料部件材料参数

图1 吸声型薄膜声学超材料胞元几何结构

基于上述构型及材料参数，联合有限元及边界元法进行仿真，建立薄膜声学超材料的声固耦合模型，如图2所示。为减少计算时间，模型中仅包含薄膜和附加质量两部分，约束薄膜边界位移用于替代外部框架。

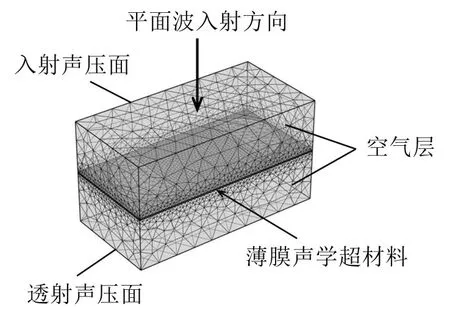
图2 吸声型薄膜声学超材料仿真模型

薄膜声学超材料上下表面设定两部分空气层（设定声速为343 m/s）：设定薄膜上部空气层为入射声压面，并设置声压幅值p0=1.0 Pa，平面波从法向入射至薄膜；薄膜下部空气层定义为透射声压面；上下两部分空气层的四周均定义为完全反射表面，用以模拟阻抗管试验。通过仿真分析，分别获取入射及透射声压面的平均声压幅值pi和pt，采用式(9)计算其吸声系数

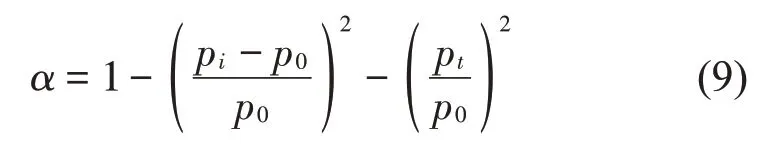
同时，制作薄膜声学超材料的小型试样，进行常规室内阻抗管的吸声系数试验，试验装置示意图见图3。图4 中实线（红色）展示了薄膜声学超材料吸声系数的仿真结果，并与用虚线（黑色）表示的常规室内阻抗管试验结果进行对比，发现两者的峰值频率特征与幅值特征均基本吻合，误差主要来源于薄膜张力误差及附加质量厚度误差。

图3 吸声系数试验装置示意图

图4 吸声系数的仿真与试验结果对比

由图4 可知，在100 Hz～1 000 Hz 频段内，吸声系数仿真结果中共出现3个吸收峰，频率依次为202 Hz、378 Hz 和705 Hz，对应峰值幅值依次为0.473、0.172和0.342。

2.2 吸声效果分析

为进一步探究吸收峰产生的原因和其幅频特征，基于弹性波动理论，采用有限元法，求解声学超材料结构的前3 阶模态振型，如图5 所示。观察可知，薄膜声学超材料的1 阶振型为附加质量沿垂直于薄膜方向振动，带动附加质量之间的薄膜振动；2阶振型为薄膜与附加质量沿垂直方向的耦合振动，两者振动方向相反；3 阶振型为薄膜沿垂直方向振动，附加质量处于平衡位置。

由弹性波动理论可知，薄膜声学超材料的吸声性能来自于薄膜的弹性应变能。由图5可知，1阶振型为附加质量带动薄膜振动，2、3阶振型中的附加质量均抑制薄膜振动，且2 阶振型中附加质量与薄膜振动方向相反，抑制作用更加强烈。因此，吸声性能应是1 阶共振＞3 阶共振>2 阶共振。这一变化规律与吸声系数的峰值幅值从高到低依次为第一吸收峰、第三吸收峰及第二吸收峰基本吻合。此外，通过对比观察3阶结构模态频率与3个吸收峰频率发现，二者吻合度很好，相差不超过1 Hz。因此表明，吸声系数曲线中的吸收峰是因超材料结构共振所致。

图5 吸声型薄膜超材料前3阶模态特征

计算薄膜弹性应变能并与吸声系数做比较，如图6 所示。可以发现，薄膜弹性应变能及超材料吸声系数的频谱特征基本一致，其频率误差不超过5 Hz。此外，两者峰值的幅值从高到低，均为第一吸收峰、第三吸收峰及第二吸收峰，两者呈正相关。

图6 薄膜弹性应变能与吸声系数对比

综上可以表明，薄膜超材料吸声系数的吸收峰主要来源于薄膜的弹性振动：在共振条件下，声能量转化为薄膜的弹性应变能；薄膜振动幅度越大，弹性应变能量越高，吸声系数的吸收峰值越大。

3 材料几何参数对吸声系数的影响

3.1 计算工况

为有效改善薄膜超材料吸声性能，拓展吸收峰带宽，本文将分别研究材料及几何参数对薄膜超材料吸声性能的影响规律，初步确定关键影响参数对各吸声峰的调控机制。

针对材料特征参数，分别改变薄膜和附加质量的制作材料，具体材料属性如表2 和表3 所示；针对结构几何参数，保持轴对称的附加质量间距不变，沿垂直于附加质量对称轴方向，分别改变薄膜两侧长度以及附加质量的半径，如图7和表4所示。以工况1为参考工况，依次改变薄膜材料、附加质量材料、薄膜总长度及附加质量半径，采用同样的边界条件，计算共13个工况下薄膜超材料的吸声系数曲线。

表2 薄膜的材料参数（附加质量材料：铸钢）

表3 附加质量的材料属性（薄膜材料：聚乙烯）

表4 几何参数工况

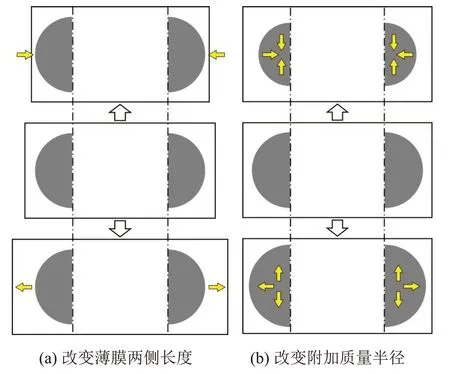
图7 不同几何参数的薄膜超材料单胞结构

3.2 材料参数对吸声系数的影响

为探究材料参数对薄膜超材料吸声系数的影响机制，首先改变薄膜材料，观察吸声型薄膜超材料的吸声系数随薄膜材料的变化规律，如图8(a)所示。

可以发现，第一吸收峰不受薄膜材料的影响，其幅频特征几乎无任何变化；第二、三吸收峰逐渐向高频移动，峰值逐渐降低，薄膜材料依次为PVC、尼龙、聚乙烯及BOPP。比较这4种薄膜材料的特征参数，如图8(b)所示，可以看出薄膜材料的密度随着依次逐渐降低，但材料的泊松比及弹性模量的变化则无显著的规律性。随着薄膜密度减小，薄膜超材料的总质量减小，导致以薄膜振动为主的第三吸收峰及以耦合振动为主的第二吸收峰向高频移动；同时随着薄膜密度减小，薄膜的总弹性应变能降低，致使第二、三共振峰幅值降低。

图8 吸声系数随薄膜材料参数的变化规律

同样地，对比观察薄膜超材料吸声性能随附加质量材料的变化规律及附加质量材料的特征参数变化，如图9所示。可以发现，与上述薄膜材料的影响机制相似，超材料吸声系数随附加质量材料的变化规律与附加质量的密度直接相关：附加质量的密度越小，固有频率越大，第一、二吸收峰越向高频移动；同时，附加质量密度越小，对薄膜振动的抑制作用效果降低，使第二吸收峰幅值逐渐增大。第一吸收峰幅值无显著变化是因为吸声系数与薄膜弹性应变能直接相关，附加质量的振动能量对其影响较小；而第三吸收峰的幅频特征无显著变化，则是因为主要参振质量（薄膜）与材料特征参数的改变对象（附加质量）不一致所致。

图9 吸声系数随附加质量材料参数的变化规律

综上可知，无论是改变薄膜材料还是附加质量材料，薄膜超材料的吸声性能均直接与材料密度相关：材料密度减小会引起整体结构的总质量降低，使以材料改变对象振动为主的振型对应的共振峰值及以耦合振动为主的振型对应共振峰值均向高频移动；薄膜材料密度减小会引起第二和第三共振吸收峰幅值降低，而附加质量材料密度减小会引起第三共振吸收峰幅值升高。

3.3 几何参数对吸声系数的影响

图10(a)展示了薄膜声学超材料吸声性能随薄膜总长度的变化规律，可以发现，随着薄膜总长度减小，第二、三吸收峰均向高频移动，第二吸收峰峰值逐渐降低，第三吸收峰峰值逐渐升高，如图中黑色箭头所示。这是因为薄膜总长度越小，相同约束下薄膜的张力越大，固有频率越高；同时由于薄膜总长度增加，致使薄膜与附加质量的耦合关系减弱，以两者耦合振动为主的第二阶振型很难被激起，而以附加质量间薄膜单独振动为主的第三阶振型将产生更多的弹性应变能，吸声系数略微升高。此外，由于改变的是薄膜总长度，对附加质量影响较小，故因附加质量振动引起的第一吸收峰的幅频特性变化很小。

随后改变附加质量半径大小，观察吸声系数随附加质量半径的变化规律，如图10(b)所示。由图可知，第一、二吸收峰的幅频特征随附加质量半径的增加而有显著变化，而第三吸收峰的幅值和频率则几乎无任何变化：第一、二吸收峰均向高频移动，第一吸收峰幅值升高，而第二吸收峰幅值降低。这一变化规律也与薄膜受力直接相关：附加质量半径的增加会导致薄膜张力增大，使超材料结构共振频率增加；两者耦合关系降低，使第一、二吸收峰幅值发生显著变化。

图10 吸声系数随薄膜及附加质量几何参数的变化规律

综上，无论是减小薄膜两侧长度或是增加附加质量半径，均会引起薄膜张力的增加，使振型以薄膜或附加质量振动为主的共振吸收峰及以两者耦合振动为振型的共振吸收峰向高频移动；同时，导致薄膜和附加质量之间的耦合关系减弱，使耦合共振峰的幅值降低，以薄膜或附加质量为主的共振吸收峰幅值升高。

4 结语

(1)薄膜超材料吸声系数的吸收峰主要来源于薄膜的弹性振动；在共振条件下，声能量转化为薄膜的弹性应变能；薄膜振动幅度越大，弹性应变能量越高，吸声系数的吸收峰值越大。

(2)薄膜和附加质量的密度改变均会引起薄膜声学超材料整体质量的变化，导致吸收峰的幅频特征发生显著变化；但两者材料的泊松比及弹性模量对薄膜声学超材料吸声性能的影响则无明显的规律性。

(3)薄膜及附加质量的几何参数变化均会引起薄膜张力发生改变，导致吸收峰的幅频特征发生显著变化。因此，可针对目标频谱特性，通过优化薄膜及附加质量几何及材料密度参数，有效改善薄膜声学超材料的吸声性能。