某混凝土面板堆石坝数值模拟与监测分析

宋志荣

(深圳市水务规划设计院股份有限公司，广东 深圳 518000)

1 概述

对于混凝土面板堆石坝而言，坝体的渗流状况和应力变形对大坝安全运行有着重要的影响作用。近些年来混凝土面板堆石坝以自身的优点得到较快发展和广泛应用[1]，天生桥和水布垭[2]等高混凝土面板堆石坝不断建成，坝体的安全也越来越受工程界与社会的关注，使其坝体应力变形及渗流成为众多相关学者的研究课题[3-4]。然而相关研究较多仅是进行了理论计算分析[5-6]，缺乏对应的监测资料，更是缺乏连续完整的监测资料，因此未进行验证分析。鉴此，本文围绕着某混凝土面板堆石坝施工完建期及蓄水期开展了有限元模拟计算，获取了大坝应力变形规律和坝体渗流情况，并结合大坝连续十几年完整的安全监测资料，将理论计算结果与原型观测数据进行相互验证分析，有效地将理论计算与大坝实际运行状态紧密的联系起来。通过进一步了解各工况下面板堆石坝应力变形规律[7-8]，为大坝后期安全运行及维护提供指导，以确保大坝保持良好的运行性态。

2 工程概况

某水库位于重庆市开县境内，坝址处于长江支流小江的二级支流桃溪河流域，是以供水与灌溉为主，兼顾发电等综合利用效益的水利枢纽工程。水库大坝为混凝土面板堆石坝，库容总量为10 240万m3，属于大(2)型水利枢纽工程，河床建基面高程350 m,最大坝高103.80 m，坝轴线长243 m，坝顶宽8 m。为了掌握大坝的运行性态，同时对大坝安全鉴定提供科学依据，大坝布置了坝体变形监测、应力监测及渗流监测等安全监测项目[9]。在坝体及坝基处共安装了16支渗压计，对坝体坝基进行了渗流监测。大坝采用一个监测点安装沉降仪和水平位移计结合的方式，对大坝的沉降和水平位移情况进行监测，在不同断面及不同高程处共安装了10支沉降仪和10支水平位移计。混凝土面板对大坝的防渗至关重要，面板的好坏直接关系到坝体的安全，为监测坝体内部及面板的应力变形情况，在混凝土面板上安装了10支两向应力计、2支无应力计和5支倾斜仪。其最大坝高处横断面坝体材料分区情况及部分监测仪器布置如图1所示。

图1 最大坝高处坝体横断面示意(单位：m)

3 有限元计算

3.1 渗流计算模型

根据工程地质水文勘察资料，地下水以裂隙水和

孔隙水赋存于泥与砂岩中，属于透水层和隔水层相间分布的多含水层水文地质结构，坝址区存在少量的断层，且规模较小，断裂不发育，根据岩体渗透性，模型中断裂岩体用分区等效连续介质模拟[10]。本文对正常蓄水位、设计洪水位、校核洪水位3种工况下进行渗流模拟计算[11]，计算采用二维稳定渗流有限元法，有限元模型网格划分采用4节点等参单元三角形网格，对主要的防渗措施(混凝土面板、防渗帷幕等)进行加密网格单元处理。该模型经网格划分后，共生成2 961个单元，1 586个节点。经网格划分后渗流计算模型如图2所示，筑坝材料的渗透系数见表1。

表1 不同区域筑坝材料渗透系数 m/s

图2 有限元渗流计算模型示意

3.2 应力变形计算模型

深覆盖层的混凝土面板堆石坝受力情况较为复杂，为了解坝体坝基的应力变形是否在合理范围内，更加明确坝体应力变形变化规律和分布情况，本文对面板堆石坝进行二维有限元模拟计算，采用的堆石体模型为邓肯E-B模型；同时，假定堆石体为非线性模型，混凝土面板为线弹性模型。在模型建立过程中，有效模拟了大坝的施工过程，采用手动方式对模型有限元网格划分，有限元网格为四边形等参单元，模型经网格划分后，生成1 988个单元，1 657个节点，其中包含135个接触面单元，应力变形计算模型及有限元网格划分如图3所示(坐标系规定如下：顺水流方向指向下游为X轴正方向，竖直向上为Y轴正方向)。

图3 有限元应力变形计算模型示意

对于堆石体材料采用邓肯E-B模型，该模型以切线杨氏模量Et和切线体积变形模量Bt两个基本量为计算参数[12]。其计算公式为：

(1)

(2)

式中Pa为大气压；K和Kb分别为杨氏模量系数和体积模量系数；n和m为切线杨氏模量Et和切线体积变形模量Bt随围压σ3增加而增加的幂次；Rf为破坏比；Sl为应力水平，其表达式为：

(3)

式中c、φ为抗剪指标。

对于卸载的情况，回弹模量由下式计算：

(4)

式中Kur为回弹模量系数。

本文应力变形计算材料参数K、n、Rf、Kb、Kur、m、c和φ由地勘资料及三轴试验确定，其邓肯E-B模型材料参数见表2。混凝土面板和趾板按线弹性材料考虑，其材料参数参照设计强度等级(C25)查《水工混凝土结构设计规范》[13](SL 191—2008)可知，弹性模量E为2.8×107kPa，泊松比ν为0.167，其容重均取24 kN/m3，抗拉强度为1 270 kPa。

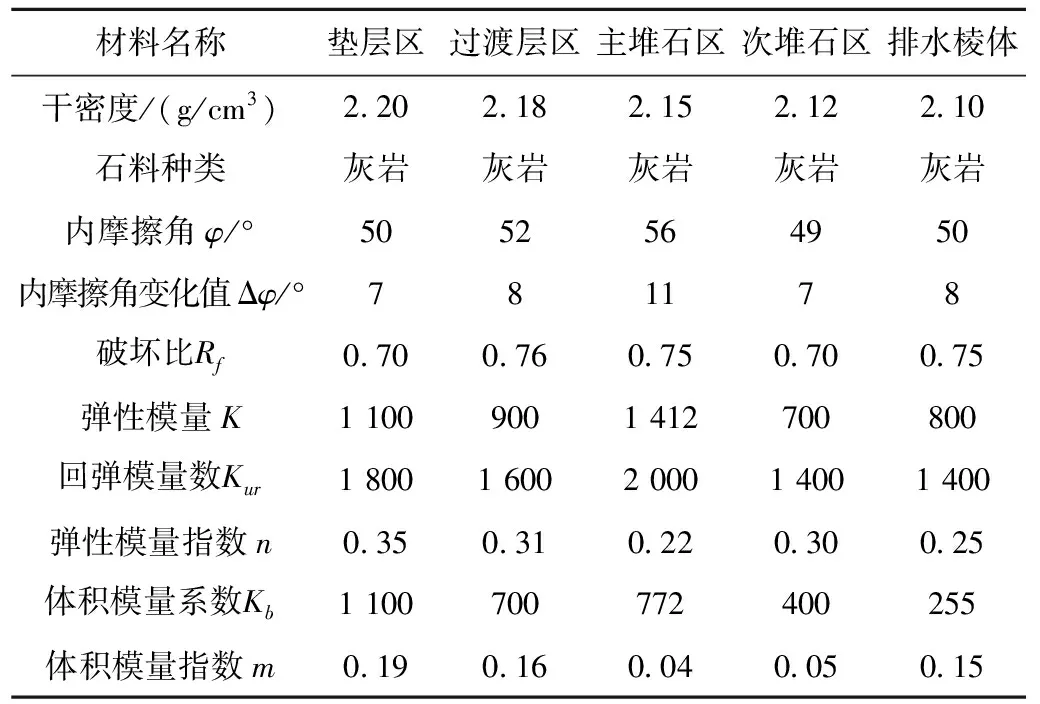
表2 应力变形计算参数表(邓肯E-B模型)

3.3 面板—垫层接触面

在混凝土面板堆石坝中，面板为混凝土材料，垫层区材料为灰岩，两者间的刚度存在较大差异，大坝受荷载作用时，此接触面常发生剪切滑移。为了能够较好地反映出面板与垫层料两者之间的相互作用，在进行有限元分析时，在面板与垫层间接触面设置接触单元，而Goodman单元能够较好地模拟接触面上的错动滑移或张开，且能够考虑到接触面变形的非线性特性[14]，故本文采用无厚度Goodman接触面4节点单元进行模拟计算分析。

在Goodman单元进行计算中，接触面上的应力和相对位移的关系为：

[σ]=[K0][ω]

(5)

二维分析中，[σ]=[τyxσyy]T为接触面两个方向的应力，[ω]=[ΔμΔν]T为接触面相对位移， [K0]为接触面的本构矩阵：

(6)

式中Kyx为切向劲度系数；Kyy为法向劲度系数。

接触面计算参数参考相关工程及经验确定，计算参数见表3。

表3 接触面计算参数

4 计算结果分析

4.1 渗流计算结果分析

大坝有限元渗流计算工况分为3种工况水位，具体工况水位见表4。

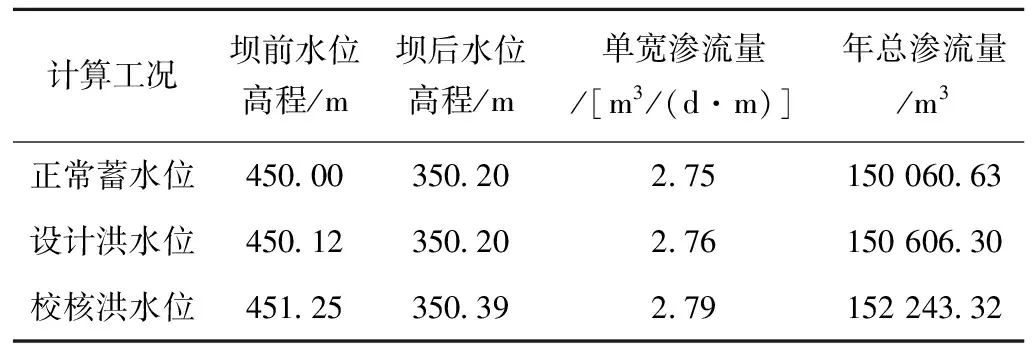
表4 渗流计算工况水位及对应渗流量

通过对3种工况水位下的渗流场计算结果分析发现，各工况下水压分布规律较为相似，但校核洪水位条件下的水头差最大，且浸润线位置最高，因此，本文仅以校核洪水位工况为例进行计算结果分析，其水压分布如图4所示。在混凝土面板堆石坝中，混凝土面板和防渗帷幕起着最重要的防渗作用[15]。坝体浸润线总体较低，在混凝土面板内由上游水位高程沿面板迅速将至约下游水位高程处，坝体下游浸润线位置接近排水棱体的底部高程，且浸润线较平缓，出逸处在下游水位高程附近，坝体内水头损失极小。混凝土面板和帷幕灌浆消散了极大部分水头差，混凝土面板后下游的坝体大部分处于疏干状态，表明混凝土面板和防渗帷幕承担了上下游水头差。所有计算工况下渗透水流均通过弱透水的混凝土面板、防渗帷幕及坝基后，几乎所有渗流量均通过排水棱体向下游流出。其单宽渗流量和年总渗流量见表4所示，单宽渗流量约为2.77 m3/(d·m)，年总渗流量约为151 151.98 m3，渗流量与水头差呈正相关趋势，即使校核洪水位下的渗流量最大，但相对总库容而言还是较小，仅占总库容的0.15%。通过渗流监测资料得知，水库水位运行至449.56 m时，量水堰计观测渗流量为5.01 L/s,相当于单宽流量为2.90 m3/(d·m),与理论计算结果较为相近，表明混凝土面板和防渗帷幕灌浆的防渗效果良好。

图4 校核洪水位下坝体坝基水压分布示意(单位：m)

4.2 应力变形计算结果分析

计算中对大坝采用有限元分级加载方式模拟大坝施工过程，先填筑坝体，后浇筑面板，再蓄水至正常蓄水位过程采用单独一级施加荷载，并考虑了大坝的工后应变情况，整个过程分为17级加载。其中，1～14级模拟坝体筑坝过程，第1级为坝基覆盖层(由于坝基为天然地基土层，地基抗变形能力远大于坝体，因此在模拟计算中不考虑地基在受自重荷载作用下的变形)，2～14级模拟坝体填筑施工；第15级模拟混凝土面板浇筑施工；第16级模拟蓄水至正常蓄水位高程450.00 m；第17级加载为模拟水库大坝蓄水后坝体的工后应变，且水平工后应变为-0.1%，竖向工后应变为-0.3%。

从图5竣工期a及蓄水期c坝体沉降等值线图可看出，不同时期坝体沉降均呈上下游对称分布，且最大沉降量位于约2/3坝高处。坝体在竣工期和蓄水期的最大沉降量分别为1.044 m、1.116 m(见表5)，分别占最大坝高的1.01%、1.08%，且蓄水至正常蓄水位后的坝体最大沉降量比施工完建期的最大沉降量增大约7.2 cm。

从图5竣工期b及蓄水期d坝体水平位移等值线图可看出，不同时期坝体水平位移也均呈对称分布，且上游坝体向上游移动，下游坝体向下游移动，水平位移最大值均位于约1/3坝高处。坝体在施工完建期向上游、下游水平位移最大值分别为0.241 m、0.363 m；坝体在蓄水期向上、下游水平位移最大值分别为0.107 m、0.397 m，向上游水平位移比竣工期减少0.134 m，向下游水平位移增大0.034 m,蓄水后向上游水平位移出现回弹现象，变化情况均在合理范围内。

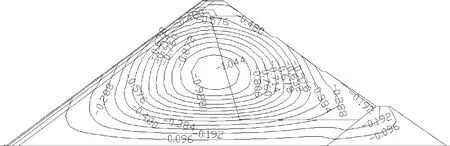
a 竣工期沉降等值线

b 竣工期水平位移等值线

c 蓄水期沉降等值线

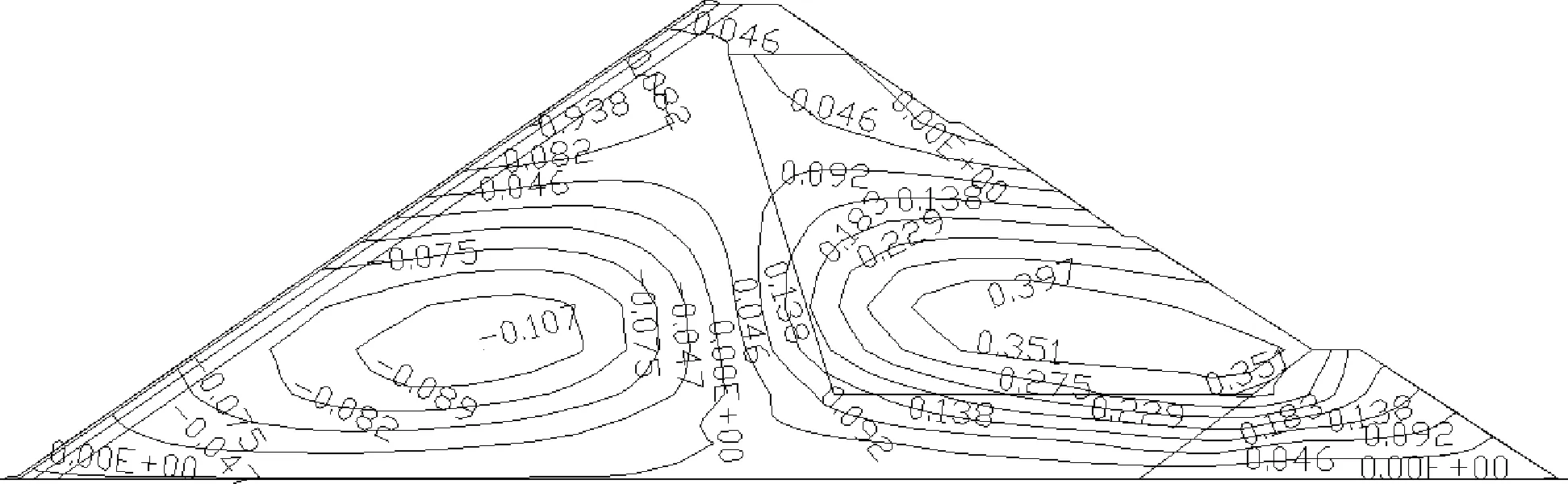
图5 竣工期及蓄水期坝体沉降、水平位移等值线示意(单位：m)

通过原型观测资料得知，坝体在施工完建期与蓄水期的最大沉降分别为1.081 m、1.205 m，且不同时期坝体水平位移监测值与理论计算值的差值均小于0.1 m，与理论计算较为相近，表明不同时期坝体沉降和水平位移分布规律与监测情况基本吻合，理论计算值比实际监测值较为相近，坝体变形规律也符合面板堆石坝的一般变形规律。

计算结果的应力值均为单元形心点之值，压应力为正值，拉应力为负值。从图6可看出，施工完建期和蓄水期的坝体大、小主应力均匀分布，且分布规律相似，坝体内没有出现应力集中区和拉应力区，但在趾板处出现小部分的应力集中现象，趾板处最大压应力值172.921 kPa远小于C25等级混凝土的抗压强度，故不构成破坏作用。竣工期的坝体应力主要受自重荷载的作用，竣工期的坝体大主应力最大值为1 502.34 kPa(见表5)，小主应力最大值为481.871 kPa，均位于坝体底部中间区域。水库蓄水后，坝体受水压力和自重荷载的共同作用，坝体上游侧部分堆石区的大小主应力受水压力影响显著，大小主应力值均出现增大现象。蓄水期坝体的大主应力最大值1 630.297 kPa，比施工期坝体的大主应力增加约127.957 kPa；小主应力最大值为557.937 kPa，比施工期坝体的小主应力增加约76.066 kPa。蓄水后趾板的小主应力显著减小，未出现突变区域。此理论计算结果与其他类似工程[16-17]计算结果相似，且与大坝安全监测值较为接近,均在允许范围内，可见坝体应力变形有限元理论计算结果基本合理。

表5 堆石体的位移和应力最大值

a 竣工期大主应力等值线

b 竣工期小主应力等值线

c 蓄水期大主应力等值线

d 蓄水期小主应力等值线

5 结语

基于非线性有限元法对某混凝土面板堆石坝在不同工况下的渗流场及应力变形场进行了模拟计算[18]，将计算结果结合监测数据分析得出以下主要结论：

1) 坝体的渗流、应力和变形计算结果均在合理的范围内，其变化和分布均符合面板堆石坝的一般规律。

2) 水库蓄水后大坝的年总渗流量占总库容的0.15%左右，而坝体的最大沉降量占坝高的1.08%左右，由此表明坝体的渗流量与沉降量均较小，大坝处于安全状态。

3) 理论计算结果与原型监测数据基本吻合，两者间的变化和分布规律也基本一致，能够有效地对大坝渗流及应力变形进行预测分析。

4) 理论计算结果对该混凝土面板堆石坝水库的后期运行有一定的指导意义，对大坝安全鉴定提供有力的科学依据和参考价值。