小模数弧齿锥齿轮的精确建模与齿面接触仿真

王君毅 黄冠锋 李兴强 张华

摘要：双重双面法铣齿加工是小模数弧齿锥齿轮的主要加工方法，传统双重双面法的齿面啮合状况需要人工调整，过程繁琐且齿面接触质量难以保证。针对小模数弧齿锥齿轮双重双面法加工的特点，建立了双重双面法加工坐标系，按照齿面加工参数和刀具参数，由刀具的切削锥面方程，经过坐标变换推导被加工齿面的齿面方程，并计算得到齿面上关键点的坐标值，利用这些关键点坐标，可以创建理论齿面片的三维模型，进而创建了齿轮副的整体三维模型。利用计算机数值仿真技术，对齿轮副进行了齿面啮合仿真。根据仿真结果，可以调整齿面加工参数，以改善齿面的接触情况，减少目前齿面接触区要依靠人工调整的繁琐过程。在提升齿面啮合质量的同时，也提高了齿轮副的实际生产效率。

关键词：小模数弧齿锥齿轮;双重双面法;三维模型;仿真

中图分类号：TH132.421             文献标志码：A        文章编号：1009-9492（2021）12-0071-04

The Pricesion Model and Tooth Surface Contact Simulation on Small ModuleSpiral Bevel Gears

Wang Junyi1，2，Huang Guanfeng2，Li Xingqiang1，2，Zhang Hua3

（1. Guangdong Enterprise Key Laboratory of Precision Gear Digital Flexible Manufacturing Equipment Technology， Zhongshan， Guangdong528400， China;2. Zhongshan MLT CNC Technology Co.， Ltd.， Zhongshan， Guangdong 528400， China;3. College of Mechanical and ElectricalEngineering， Zhongshan Polytechnic， Zhongshan， Guangdong 528437， China）

Abstract： Duplex  spread-blade  method  is the  main  processing  of traditional  small  module  spiral  bevel  gears. For traditional  duplex spread-blade method， the meshing contact between the two tooth surfaces often depends on complex manual adjustment， which is the fundamental reason why it is difficult to improve the tooth surface contact performance. For the duplex spread-blade method， according to the gear machining parameters and head-cutter parameters， the tooth surface equation was derived from the head-cutter cone surface equation by coordinates transformation， and the coordinates of the key tooth surface points was calculated. Using the key points coordinates， the theoretical tooth surface 3D model was created， and then the 3D model of the gears were created. With computer numerical simulation technology， the tooth surface meshing status was simulated. According to simulation results， the tooth surface machining parameters can be adjusted to improve meshing performance， and reduce the process of manual contact bearing adjustment. The research can improve the tooth meshing quality， and also improve the machining efficiency of spiral bevel gears.

Key words： small module spiral bevel gear; duplex spread-blade method;3D modle; simulation

0 引言

小模數弧齿锥齿轮在相交轴传动中应用广泛，在电动工具、园林工具、缝纫设备、机械仪表、汽车等行业，市场需求量巨大。由于其模数小且生产批量大，大轮和小轮的通常采用同一把双面铣刀盘同时加工出轮齿的两个齿面，这种加工组合方法称为“双重双面法”[1]。采用“双重双面法”铣齿调整计算过程简单，具有较高的切削效率。该方法采用双重收缩设计，仅仅可以保证大、小轮在齿面计算点处的螺旋角和压力角一致，即只能保证接触区在齿面上的位置，不能保证接触区的形状，这就从根本上限制了齿轮副啮合性能的提升。在小模数弧齿锥齿轮的实际生产中，为了同时兼顾两对齿面的啮合，对于齿面接触区的调整通常依赖于加工人员的个人经验，为了得到较为理想的齿面接触区，往往需要反复调整多次，过程繁琐。

基于计算机三维建模技术，本文将根据小模数弧齿锥齿轮的齿面展成过程，构建齿面展成加工坐标系，精确再现实际刀盘锥面铣削展成齿面的过程，从而推导被加工齿轮的齿面方程，进而生成齿面片的三维模型。根据齿坯几何参数，建立齿轮副毛坯的三维模型，并结合齿面片的三维模型，最终构建整个齿轮副的三维模型。该齿轮副的三维模型，在理论上完全反映了实际齿面加工过程，是最为精确的弧齿锥齿轮三维建模方法[2-3]。本文基于精确的理论三维模型，根据齿轮副的安装要求，利用三维造型软件，可以通过虚拟装配，模拟实际齿轮副的齿面啮合状况。基于以上内容，在实际加工之前，根据理论齿面的啮合仿真，可以调整齿面加工参数以及刀具参数，提升齿面啮合质量，从而可以预控齿面接触性能，减少实际生产中接触区调整的繁琐过程。

1 齿面展成原理与齿面方程的推导

弧齿锥齿轮齿面的加工过程实际上是平面产形轮与被加工齿轮做无间隙啮合的过程，在齿面展成的任意瞬时，切削锥面上的一个点对应着被加工齿面上的一个点，这就是弧齿锥齿轮加工的平面产形轮原理。

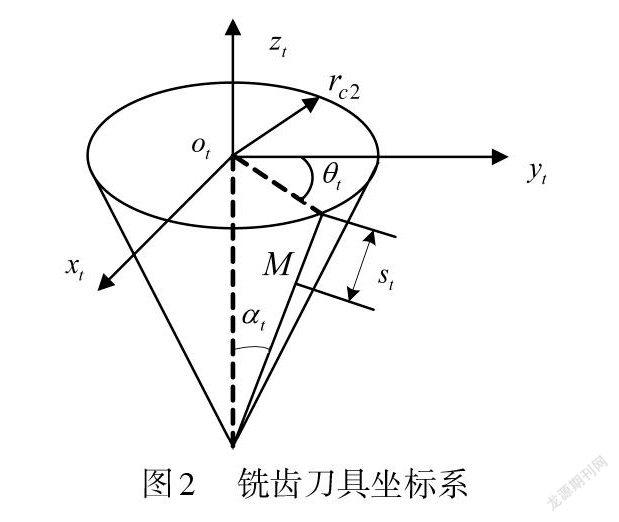
根据实际齿面的展成过程，建立如图1所示的齿面展成加工坐标系，用以描述铣齿加工过程中铣刀盘与工件之间的相对运动关系[4-5]。如图所示，根据齿轮副的加工调整参数，建立齿面加工坐标系，用以确定刀具坐标系 St 到工件坐标系 Sp 的坐标变换矩阵。如图2所示，在 St 下描述铣刀盘的切削锥面方程。在图1所示的加工坐标系中，由刀盘坐标系 St 下的切削锥面方程，通过一系列坐标变换，可推导工件坐标系 Sp 下工件的齿面方程。

根据平面产形轮原理，在坐标系 St 中所示的刀齿切削刃上任意一点，在图1中通过坐标变换，便可以计算得到对应的坐标系 Sp 中工件齿面上点的坐标。弧齿锥齿轮的齿面坐标点的计算便是依据以上过程，给定切削刀刃上一系列的点的坐标值，用刀盘转角θ t 模拟铣刀盘的回转，随着铣齿范成摇台角 q 的变化，通过坐标变换，便可以得到对应的一系列齿面点的坐标值，这些点便是创建齿面三维模型的关键数据点[6-7]。

2 小模数弧齿锥齿轮的精确建模

根据齿面展成原理，以及上节描述的齿面坐标点的计算过程，小模数弧齿锥齿轮的精确建模过程如下。

（1） 按照“双重双面法”，进行双重收缩的轮坯几何设计，以及双重双面法加工参数设计。

（2） 根据双重双面法加工参数及刀盘参数，构建图1所示铣齿加工机床坐标系，推导齿面方程，给定切削锥面上的一系列坐标点，求得齿面上的一系列坐标点[8-9]。

（3） 将齿面上的一系列坐标点进行整理，存储为 UG 等三维软件可识别的格式文件。

（4） 在 UG等三维软件中，根据轮坯几何参数构建轮坯回转截面“草图”，经“旋转”操作，构建轮坯模型;导入齿面点坐标，进行“缝合”操作，生成齿面片;用齿面片与轮坯模型进行布尔求差得到“修剪体”，生成一个齿槽;将齿槽进行“阵列”操作，得到完整的齿轮模型[10-11]。

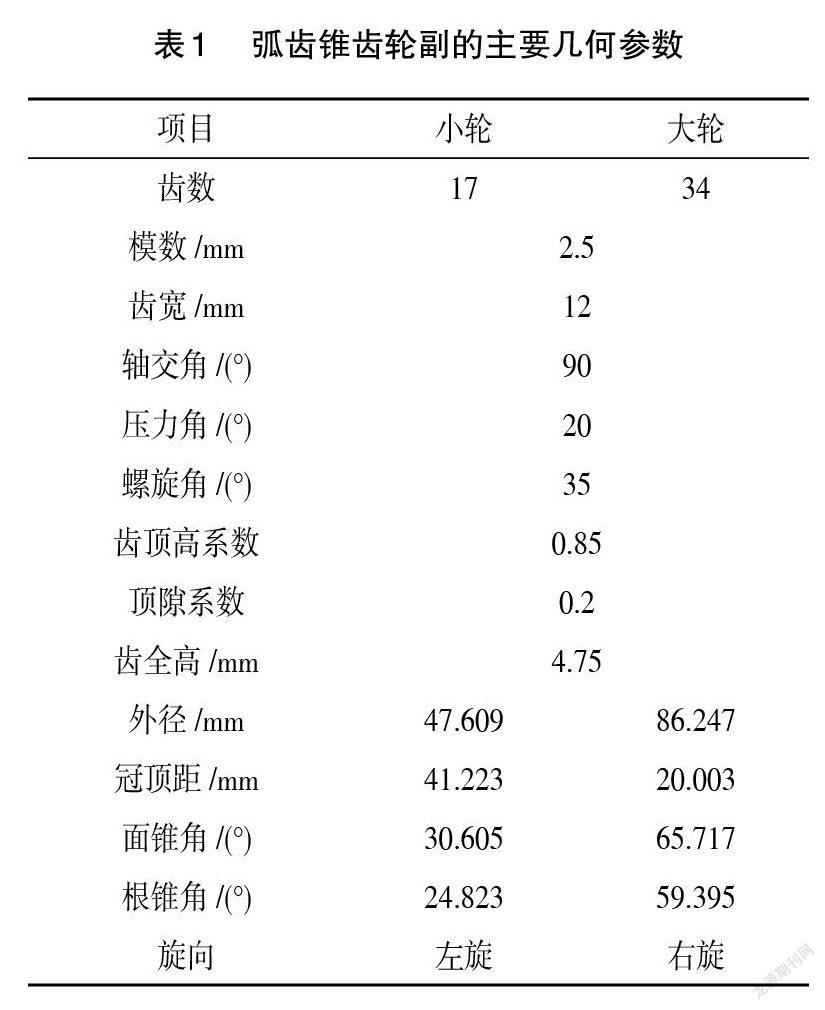
根据上述过程，以一对具体的小模数弧齿锥齿轮为例，说明以上三维建模过程。根据双重收缩设计，表1所示为齿轮副的几何参数，表2所示为齿轮副加工所用的铣刀盘和机床调整参数。

以表1中的大轮为例，建立铣齿机床加工的坐标系，推导齿面方程，生成齿面上一系列数据点坐标，整理这些坐标点，存储为 UG软件可以识别的纯文本格式的文件（如*.txt格式），文件格式举例如下：

由以上数据点拟合成的曲面片可以认为是在齿长方向取20个点，在齿高方向取15个点，共计300个数据点拟合而成。在 UG 软件的曲面操作中，利用“通过点”或者“通过极点”命令，选择以上文件，读取坐标点数据，經过 UG软件的自动拟合，可以生成一个光顺的齿面片，如图3所示。

按照表1所示的几何数据，很容易生成齿轮的轮坯模型。由图3齿面片及轮坯模型，在 UG 环境下，通过“曲面缝合”形成一个齿槽对应的曲面片，再经过“修剪体”命令生成齿槽，经“图样面”阵列后便完成了整个齿轮的三维造型。

小轮三维模型与大轮的创建过程相同，完成的弧齿锥齿轮副模型如图4所示。图中的三维模型由实际展成参数推导而来，与理论齿面完全一致，与实际加工的齿面完全一致（假设齿面不存在加工误差），该模型完全、精确地再现了实际加工齿面。根据该齿面，可以非常“直观”地观察和测量轮齿的齿厚、齿高、齿顶宽等齿部几何参数，可以判断大、小轮齿厚的分配情况，轮齿收缩是否正常，是否有根切现象等，避免了在实际加工中出现各种不良缺陷，缩短了产品试制周期，降低了产品的试制成本。

该三维模型可以用于小模数弧齿锥齿轮的粉末冶金成形，精密锻造成形;在弧齿锥齿轮的测量过程中，可以作为实际齿面的测量基准;也可以将齿轮副的三维模型导入到有限元分析软件，用来分析齿轮副的强度[12]。小模数弧齿锥齿轮的精确三维建模，为齿轮副的数字化生产和精密制造提供了重要支持。

3 小模数弧齿锥齿轮的接触仿真

在 UG的“装配”环境下，将图4中的大、小轮按照正确的图纸安装要求进行虚拟装配，设定大、小轮的节锥顶点重合，设定大、小轮的轴交角为90°，设定两接触齿面间的干涉量为0.01 mm ，用以模拟仿真齿面的接触情况。为了突出齿面接触区，设定大、小轮不同的颜色（大轮深色，小轮浅色），设定小轮具有70%的透明度，得到的两齿面间的接触印痕如图5所示，齿面瞬时接触区呈长椭圆状。需要说明的是，这里是齿面间的“干涉”，是用轻微的干涉来代替实际齿面间的接触区，并不代表真实的齿面的啮合接触，但是与真实齿面间的接触非常接近，是分析齿面接触状况的常用技术手段。由此可以检查齿面啮合接触区在齿面上的大小和位置，检查齿面接触区是否符合预期，检查齿面侧隙的大小，有无干涉、有无边缘接触等不良接触现象。用虚拟接触仿真，代替了实际试制过程中的齿面滚动检查，在加工之前可以提前调整刀具参数、加工参数，减少了生产过程中的实际调试过程。

在 UG的“运动仿真”环境下，针对装配与齿面接触仿真，建立齿轮啮合运动副。设置小轮作为主动轮以恒定转速绕自身轴线回转，同时设定大轮按照固定的传动比绕大轮轴线跟随回转，可以进行动态啮合仿真，随着轮齿逐渐进入啮合到退出啮合，可以观察接触区在两齿面间的交替变化，判断整个接触区域在齿面上的分布情况，有无出现边缘接触等。

4 结束语

小模数弧齿锥齿轮应用广泛，由于模数小，通常需要用“双重双面法”加工，加工计算过程简单，齿轮副的接触质量一般需要靠人工调整来保证，过程繁琐。本文针对“双重双面法”设计的齿坯几何及加工调整参数，对小模数弧齿锥齿轮进行了精确的三维建模。通过齿轮副的三维模型，可以检查轮齿的齿厚分配、轮齿的收缩情况，可以检查齿轮副啮合时的齿顶间隙和齿侧间隙，在真正加工之前及时调整工艺参数，避免了因返工造成的工时浪费。该精确三维模型还可以应用于快速成形制造、有限元强度分析、齿面偏差测量等。在三维造型软件环境下，将齿轮副的三维模型进行虚拟装配，可以进行齿面接触分析、轮齿啮合运动检查。针对以上内容，本文通过具体的建模实例，进行了说明。

本文根据实际机床加工过程，建立了机床加工坐标系，进行了小模数弧齿锥齿轮的精确三维建模和齿面接触仿真，为齿轮副的实际生产提供了可靠的仿真分析手段，有效提升了小模数弧齿锥齿轮的啮合质量和生产效率。

参考文献：

[1]北京齿轮厂.螺旋锥齿轮[M].北京：科学出版社，1974.

[2]张华， 刘高杰，徐林林，等.小模数弧齿锥齿轮的三维建模与应用分析[J].机械传动，2013，37（9）：42-45.

[3]张华， 张占立，魏冰阳，等.适用于模具法加工的弧齿锥齿轮精确建模[J].机械传动，2010，34（12）：20-22.

[4] Litvin F L， Zhang Y. Local synthesis and tooth contact analysis of face – Milled spiral bevel gears[R]. NASA，CR，4342.Chicago： NASA Lewis Research Center，1991：14-68.

[5] Litvin F L. Gear geometry and applied theory [M].New Jersey： Prentice Hall，1994.

[6]炊兵毅，張华，杨建军.小模数弧齿锥齿轮的切齿理论与铣齿试验研究[J].机械传动，2020，44（8）：171-176.

[7]唐进元， 蒲太平， 颜海燕.螺旋锥齿轮双重双面法多轴联动数控加工计算机仿真研究[J].制造技术与机床，2008（2）：25-29.

[8]田行斌.弧齿锥齿轮啮合质量的计算仿真和控制[D].西安：西北工业大学，2000.

[9]方宗德，杨宏斌，邓效忠.弧齿锥齿轮齿面优化修正及计算机仿真[J].航空动力学报，2002，17（1）：140-144.

[10]李旭伟， 田程， 张林涛.驱动桥锥齿轮错位量的有限元建模和分析[J].机电工程，2020，37（4）：371-376.

[11]张华，韩益南，李天兴，等.等高齿弧齿锥齿轮的三维精确建模与加工试验[J].河南科技大学学报：自然科学版，2015，36（4）：27-31.

[12]张华，程进.基于有限元的非零正传动弧齿锥齿轮的强度分析[J].现代制造工程，2019（7）：151-156.

第一作者简介：王君毅（1978-），男，工程师，研究领域为齿轮加工机床设计与数控系统开发，已发表论文2篇。

（编辑：王智圣）