基于UHBs的输气管道高后果区泄漏燃爆事故分析

迟明华，蒋宏业，赵新好，徐涛龙

(1.西南石油大学 石油与天然气工程学院，四川 成都 610500；2.油气管道技术研究院，四川 成都 610500；3.国家管网集团公司西气东输分公司，上海 200122)

0 引言

随着我国的天然气消耗的增加，越来越多输气管道穿越人口密集区等特殊场所，形成高后果区[1]；其内输气管道一旦发生泄漏燃爆事故将会造成极大破坏[2]。而在输气管道事故风险可能性影响因素中，人的不安全行为导致的第三方破坏具有突发性高、随机性大以及难以防控等特点，一直被列为4大类风险因素之首[3]。因此，基于人的不安全行为对输气管道高后果区进行泄漏燃爆事故分析具有重要意义。

Bow-tie模型是全面分析某一事件发生原因和事故后果的方法[4]，在油气管道失效和后果分析上有着一定的应用[5-6]，但Bow-tie模型存在着2个弊端：1)事件状态具有二态性，故障逻辑关系具有确定性；2)只能按照结构从底至顶逐层推理计算顶事件的发生概率，计算量大且不能逆向推理。这2点弊端限制了Bow-tie模型在工程实际上的应用，宋华等[7]所提出的T-S模糊故障树分析方法，考虑了故障概率和事件间联系的不确定性，改进了传统Bow-tie模型的弊端；胡显伟等[4]、於孝春等[8]便采用改进后的模糊Bow-tie模型(Fuzzy Bow-tiemodel，FBT)对燃气管道和深水海底管道进行定量风险评价。而贝叶斯网络(Bayesian Networks，BN)在双向计算和描述事件多态性、非确定性逻辑关系上有显著优势[9]，可以弥补Bow-tie模型的弊端。

本文结合T-S模糊故障树、Bow-tie模型和贝叶斯网络3种方法，从人的不安全行为发生的可能性出发，建立不同等级人口敏感区输气管道泄漏燃爆事故FBT-BN分析模型对输气管道高后果区泄漏燃爆事故易发性和事故致因进行分析。

1 基本理论和方法

1.1 基于T-S模糊故障树的模糊Bow-tie模型

引入T-S模糊故障树[7]，建立基于T-S模糊故障树的模糊Bow-tie模型，简单模型如图1所示。

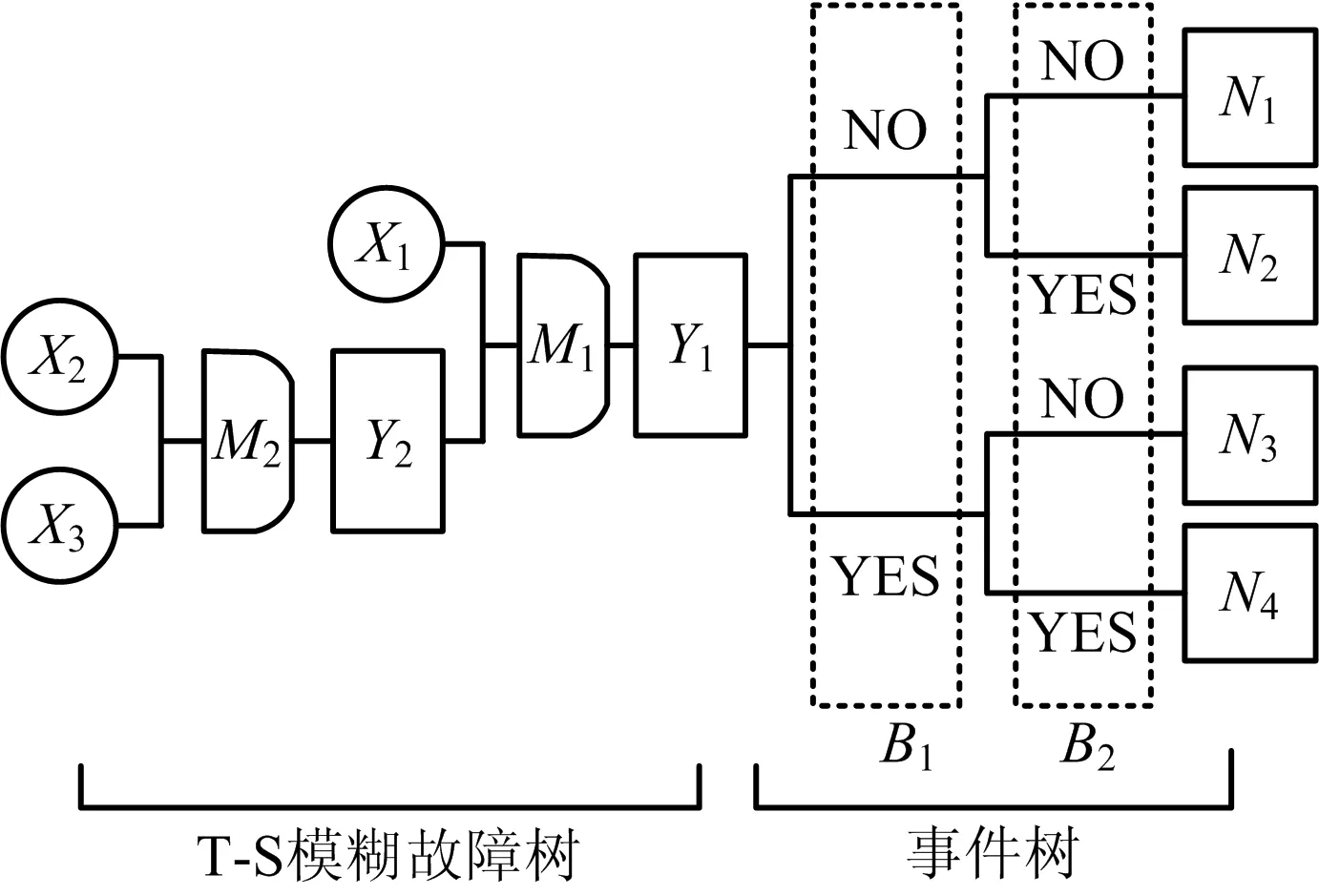
图1 简单模糊Bow-tie模型示意

Y1为事故事件，Y1左边为T-S模糊故障树，其中：X1～X3为基本事件，Y2为中间事件，M1与M2为T-S模糊门；右边是以事故事件Y1为基础，根据事故发生后可能产生的后果所建立的事件树，其中：N1～N4为后果事件，B1和B2为安全屏障，YES与NO为安全屏障规则。

1.2 贝叶斯网络

贝叶斯网络是1种图论与概率论相结合的赋值因果图。给定根节点发生概率，无须求解割集，便可利用联合概率分布直接计算叶节点的发生概率[10]。

1.3 模糊Bow-tie模型向贝叶斯网络转化方法

应用T-S模糊故障树和事件树分别转化的方法将模糊Bow-tie模型转化为贝叶斯网络[11-12]。

具体转化方法如下：

1)T-S模糊故障树部分

将T-S模糊故障树中的基本事件、中间事件和顶事件分别作为贝叶斯网络中的根节点、中间节点和叶节点，当存在多个相同的事件时，在贝叶斯网络中只需建立1个节点；用有向边来连接贝叶斯网络中对应的节点；利用T-S门规则对贝叶斯网络中对应节点的条件概率表进行赋值。

2)事件树部分

将事件树中的安全屏障、事故后果分别作为贝叶斯网络中的根节点、叶节点，两者之间用有向边进行连接，利用安全屏障规则对贝叶斯网络中对应节点的条件概率表进行赋值。

其转化流程框图如图2所示。

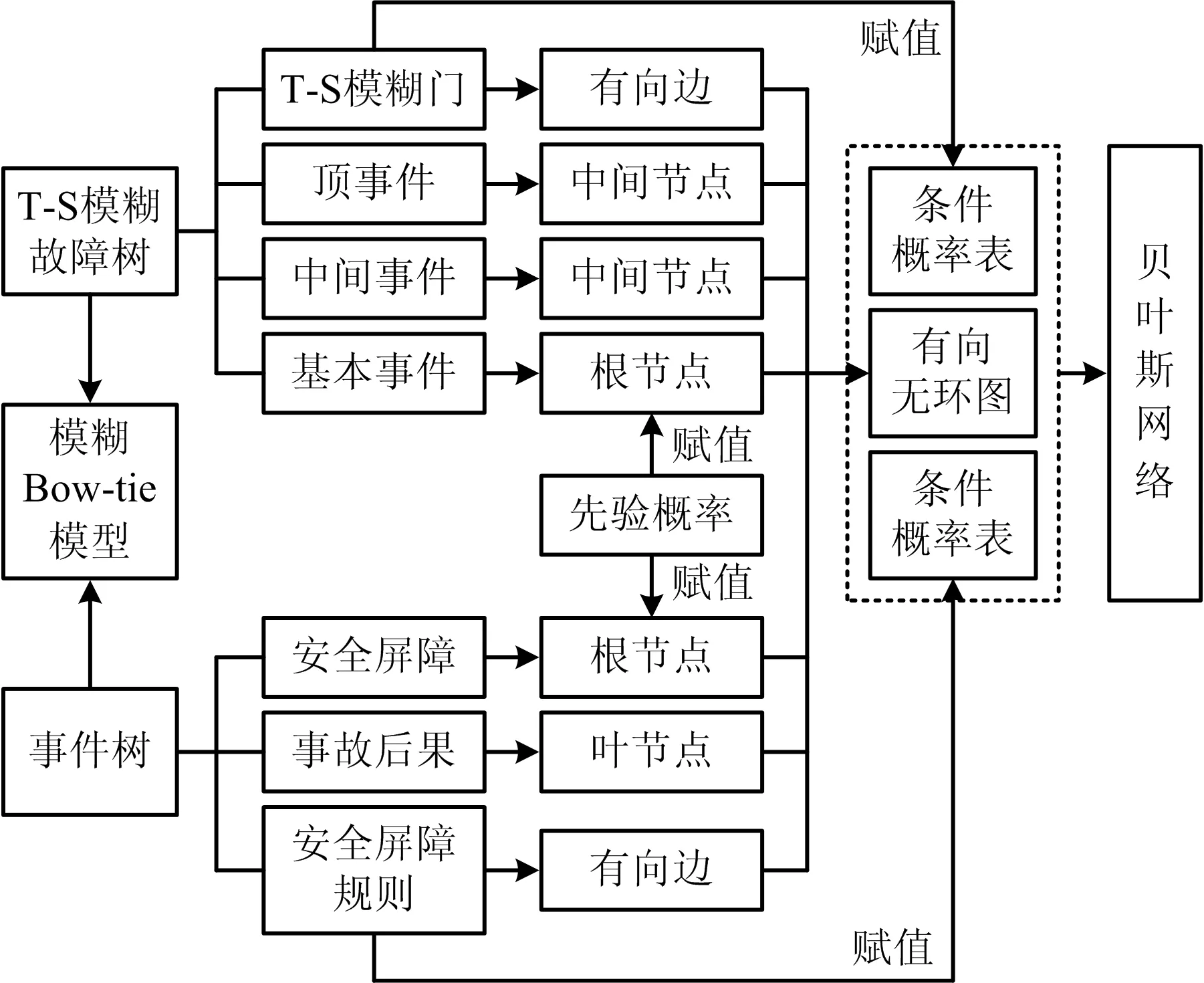
图2 基于模糊Bow-tie模型构造贝叶斯网络流程

2 构建输气管道泄漏燃爆FBT-BN模型

2.1 建立模糊Bow-tie模型

以西南某输气管道高后果区为例，从人的不安全行为出发，对风险源进行辨识，得出基本事件见表1，建立起以输气管道泄漏为事故事件的T-S模糊故障树；再以输气管道泄漏事件为基础，根据常见事故后果，用不同事故发生的触发条件替代安全屏障，建立起燃爆事件树，最终构建出输气管道泄漏燃爆模糊Bow-tie模型，如图3所示。

表1 基本事件符号及描述

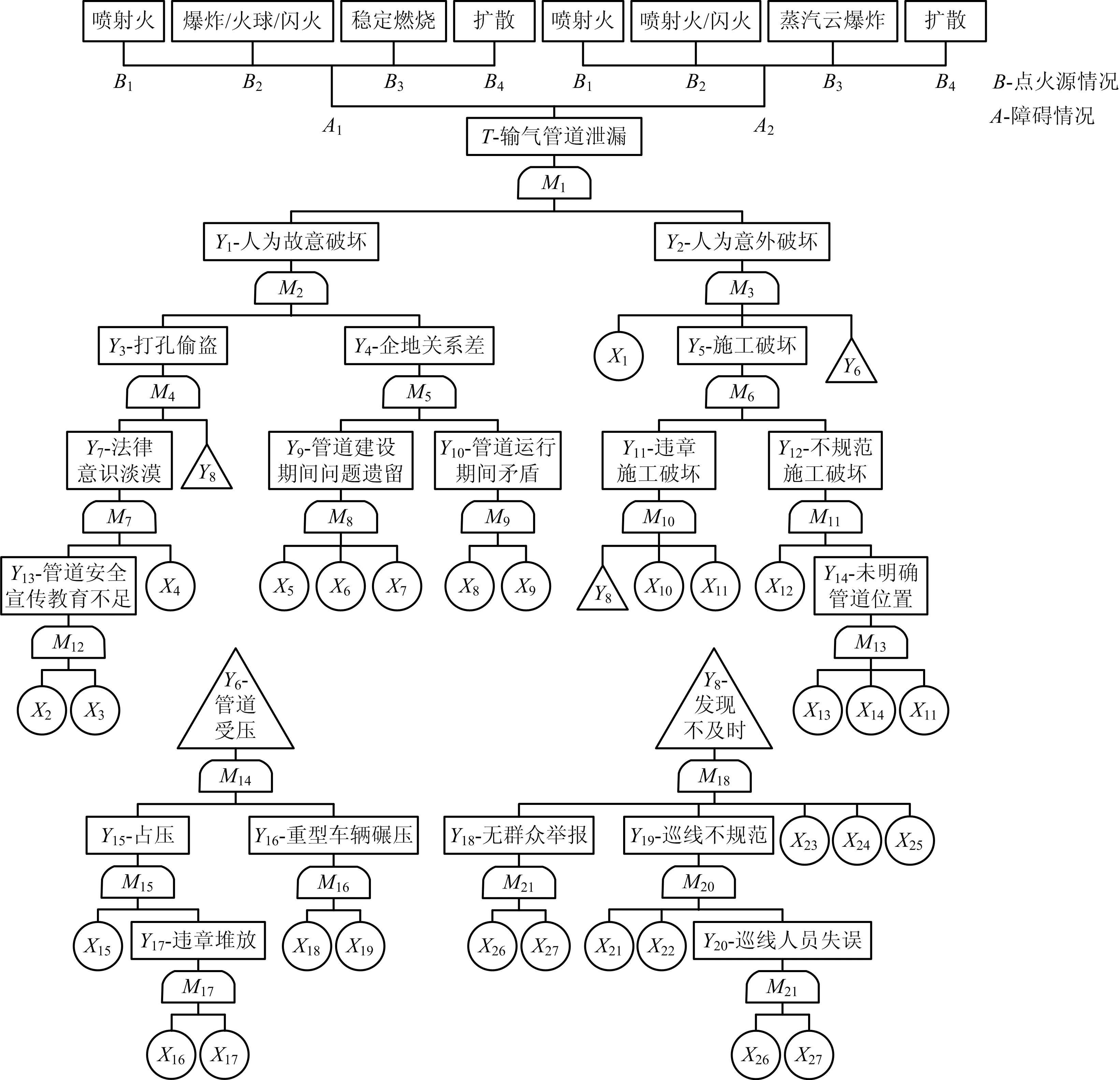
图3 输气管道泄漏燃爆模糊Bow-tie模型

其中：T为顶事件，M1～M21为T-S模糊门，X1～X27为基本事件，Y1～Y20为中间事件，A1～A2与B1～B4为规则，分别为：A1(有障碍限制扩散),A2(无障碍限制扩散),B1(立即点燃),B2(当地延迟点燃),B3(远距离延迟点燃),B4(无点火源)。

2.2 基于模糊Bow-tie模型构建贝叶斯网络

在GeNIe软件中绘制输气管道泄漏燃爆贝叶斯网络，如图4所示。

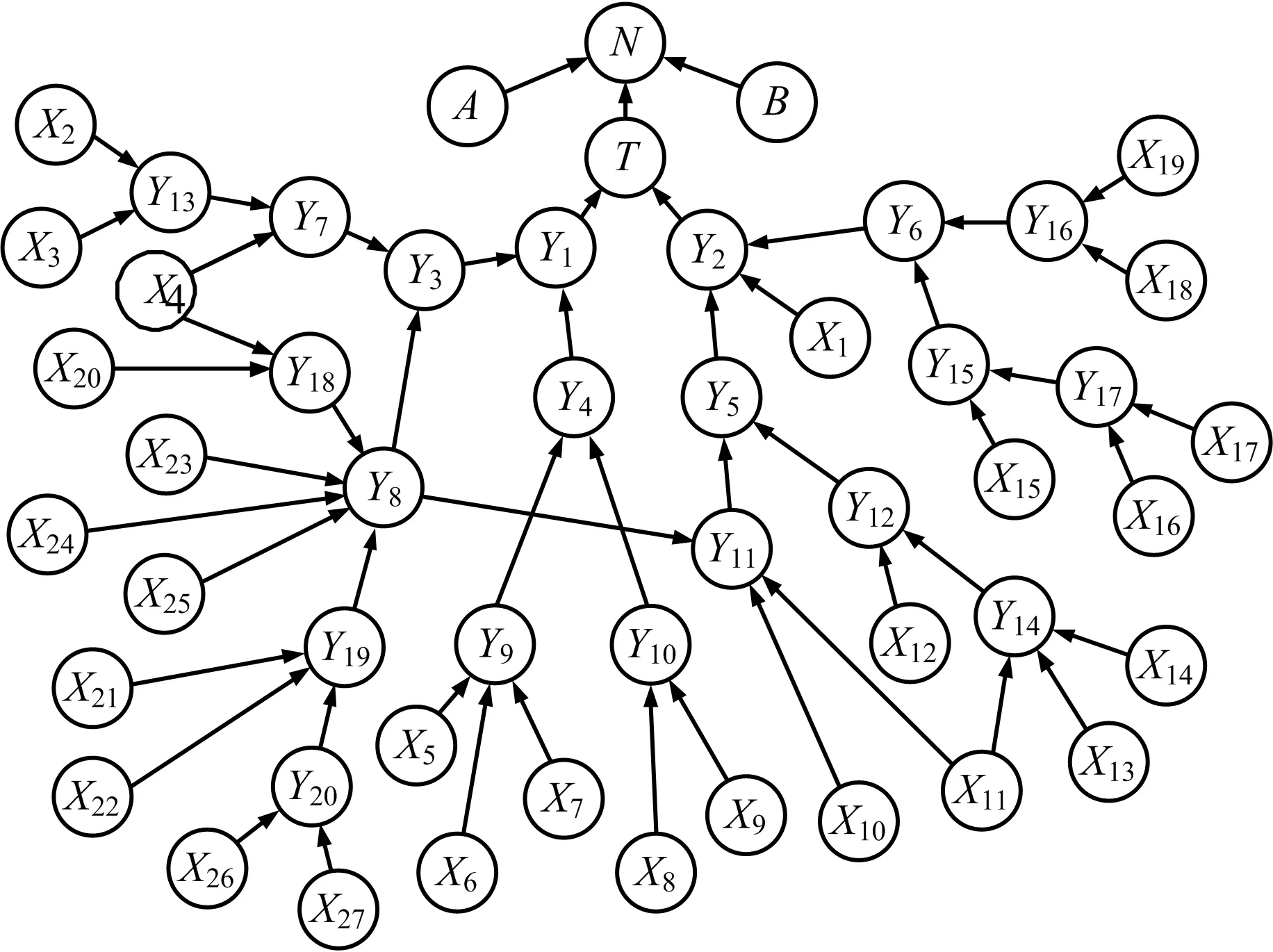
图4 输气管道泄漏燃爆贝叶斯网络

将图3中事件树所述的喷射火、闪燃、蒸气云爆炸、火球统一视为燃爆事故，即N有3个状态(燃爆/泄漏/无)，A具有2个状态(有障碍限制扩散/无障碍限制扩散)，B具有4个状态(立即点燃/当地延迟点燃/远距离延迟点燃/无点火源)。

2.3 基于高后果区等级的人口敏感等级划分

依据《油气输送管道完整性管理规范》[13]中对高后果区的描述，将其按人的不安全行为发生的可能性定义为不同等级人口敏感区，人口敏感等级划分见表2。

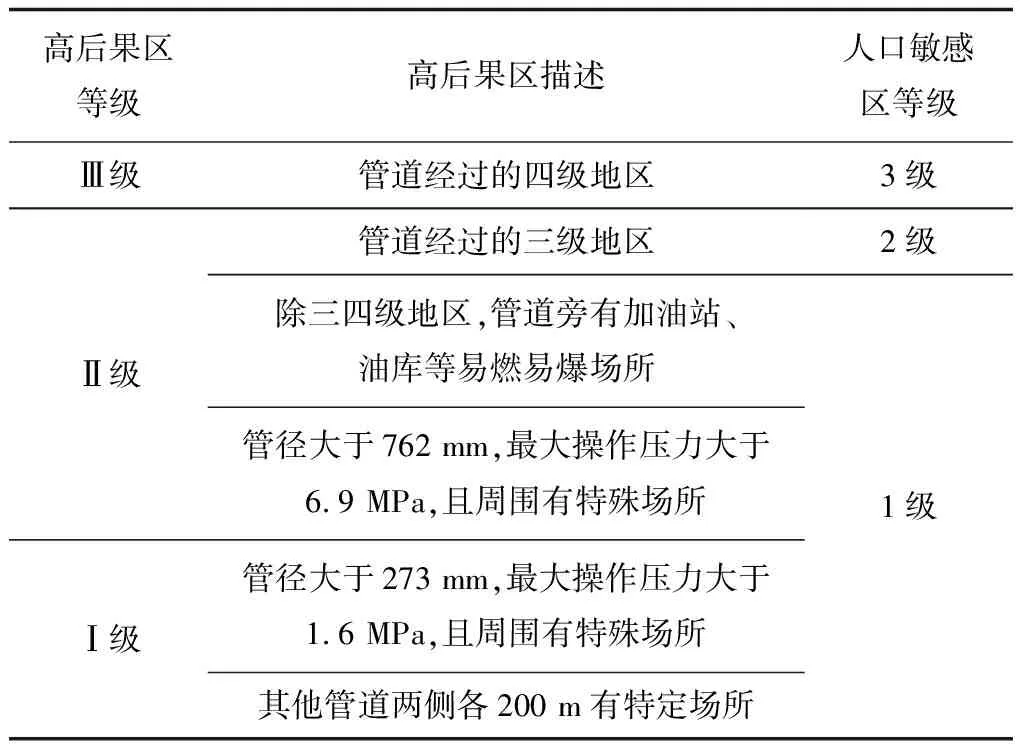
表2 人口敏感等级划分

2.4 根节点先验概率的确定

由于无法基于统计得到基本事件的发生概率，采用专家经验评判法确定基本事件的发生概率。

以基本事件X1为例，经评判，基本事件X1在3级人口敏感区发生的可能性为高，依据事件发生概率评分准则，见表3[14]，得出发生概率评分等级为7，对应的概率值为0.025。因此在贝叶斯网络中，根节点X1在3级人口敏感区的先验概率为(0.025,0.975)。同理，可得到不同等级人口敏感区各根节点的先验概率，各根节点先验概率分布见表4。

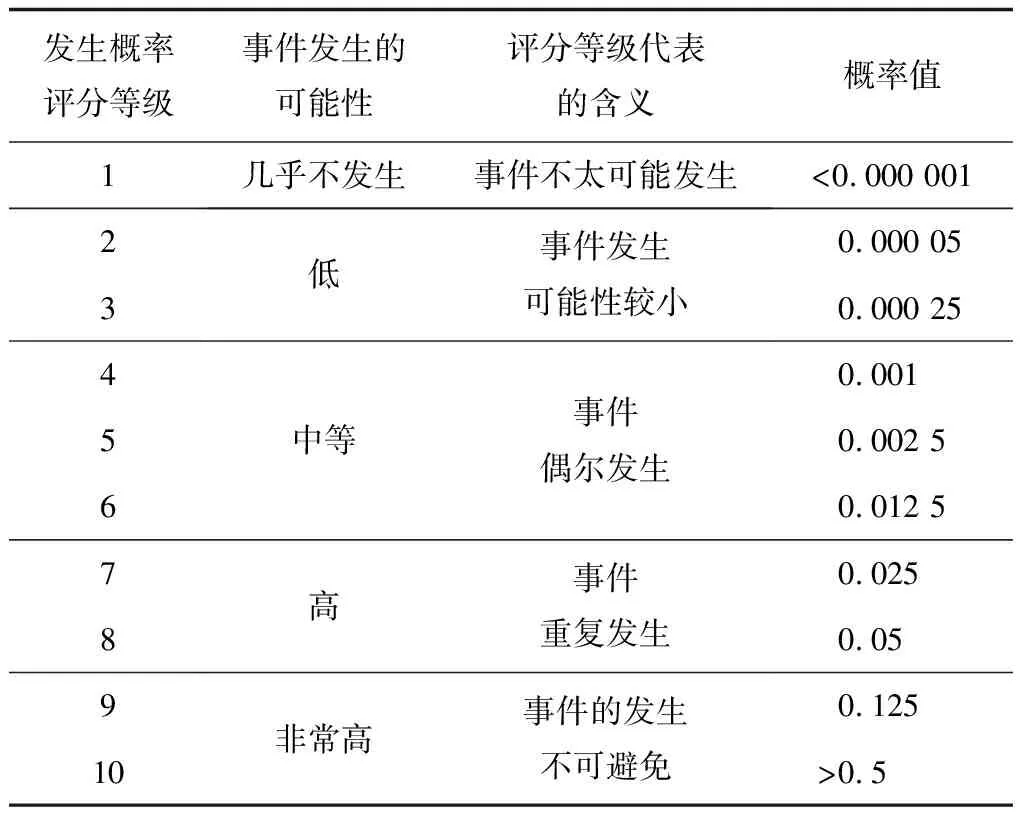
表3 事件发生概率评分准则

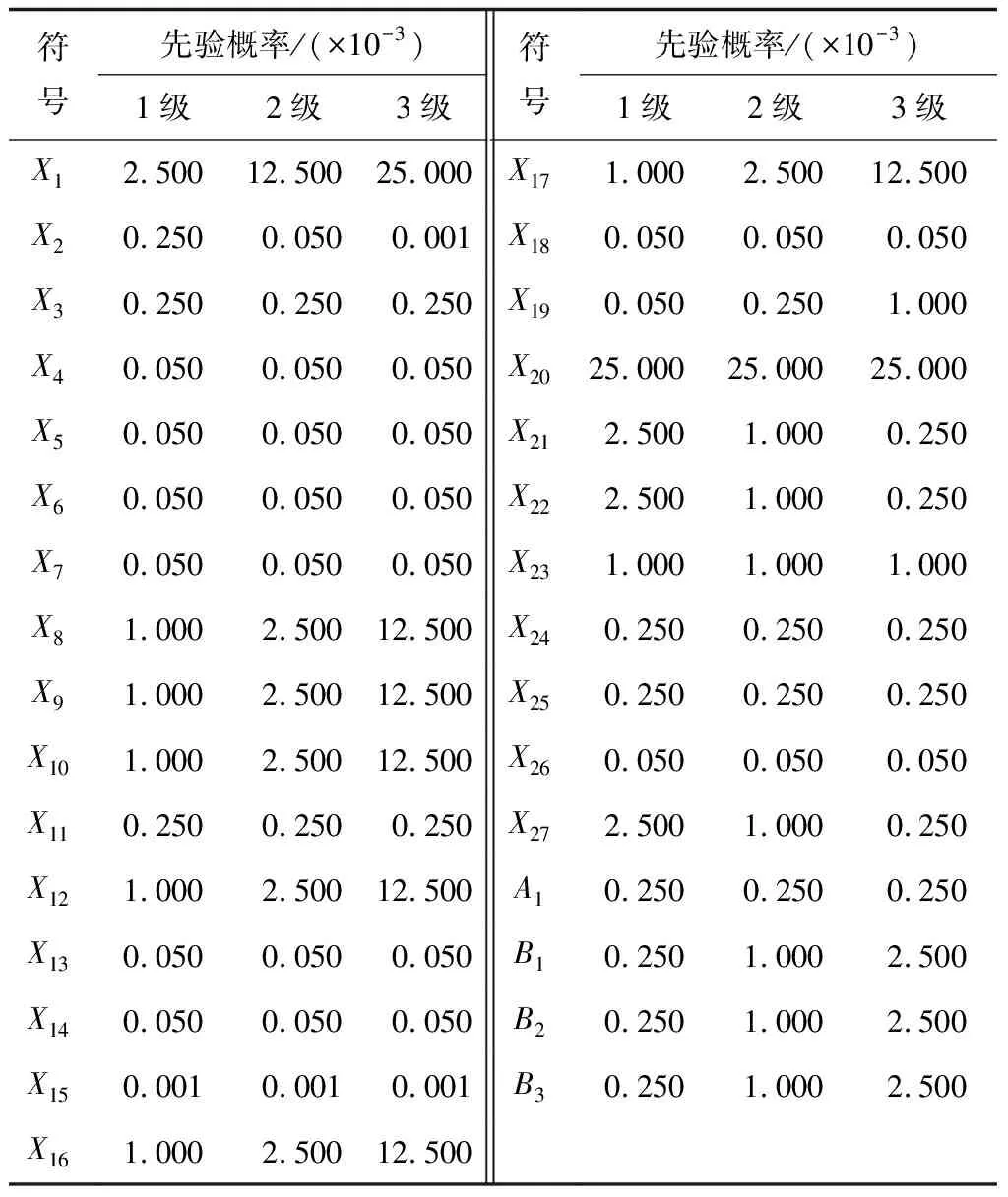
表4 根节点先验概率分布

2.5 中间节点条件概率表的确定

以中间节点Y2为例，Y2有X1,Y5,Y63个父节点，若按传统故障树中或门的逻辑，当X1,Y5,Y6中任一事件发生，Y2均会发生；但在实际情况中，X1和Y6的发生可能并不会导致Y2的发生，因此需要结合实际情况和T-S模糊门对中间事件条件概率表进行赋值，传统故障树和T-S模糊故障树2种方法下Y2的条件概率表见表5。

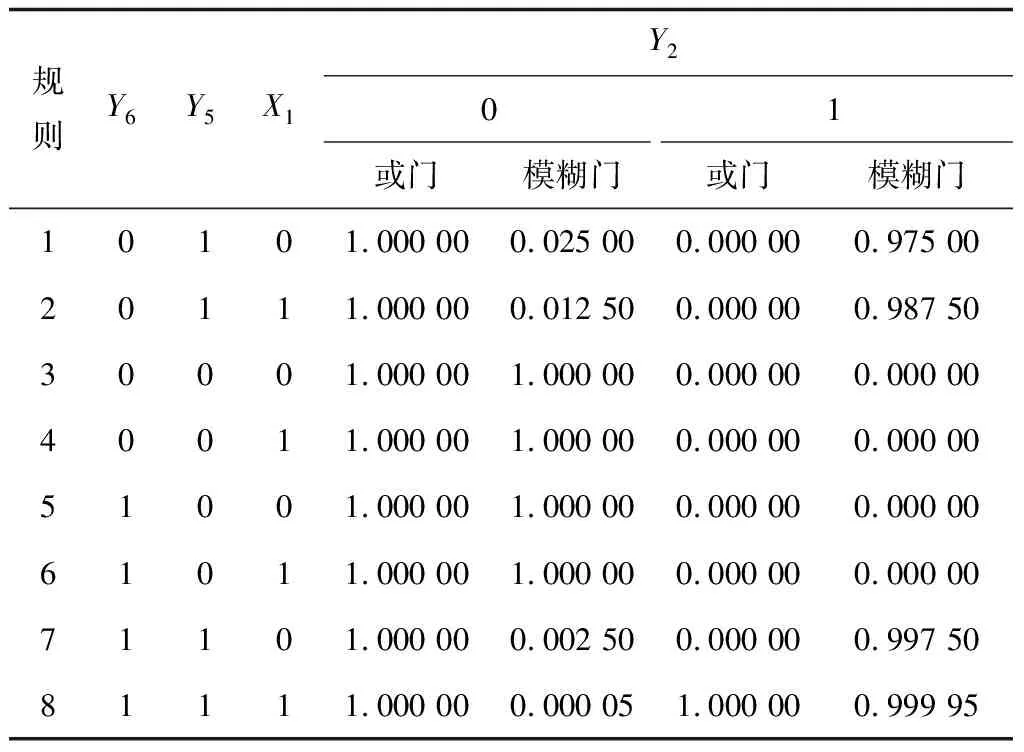
表5 2种方法下Y2的条件概率表

规则1表示：在Y6状态为0，Y5状态为1，X1状态为0的条件下，Y2为状态0的可能性为0.025、为状态1的可能性为0.975，其他规则以此类推。

3 结果分析

3.1 泄漏燃爆事故易发性分析

通过贝叶斯网络进行正向推理计算，得到不同等级人口敏感区泄漏燃爆事故发生的概率，见表6。不同等级人口敏感区泄漏燃爆事故概率对比如图5所示。

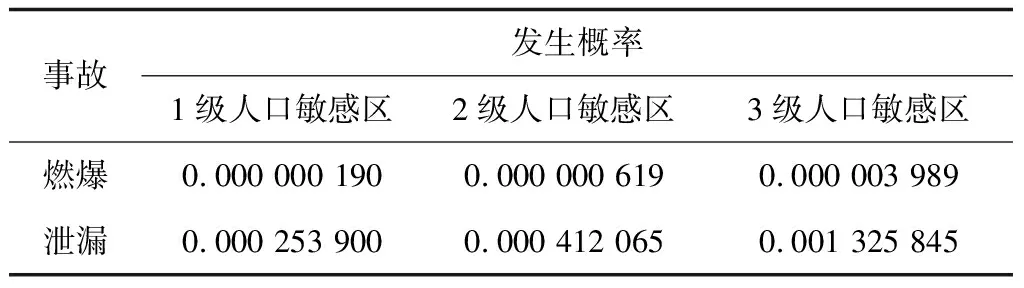
表6 不同等级人口敏感区不同事故发生概率

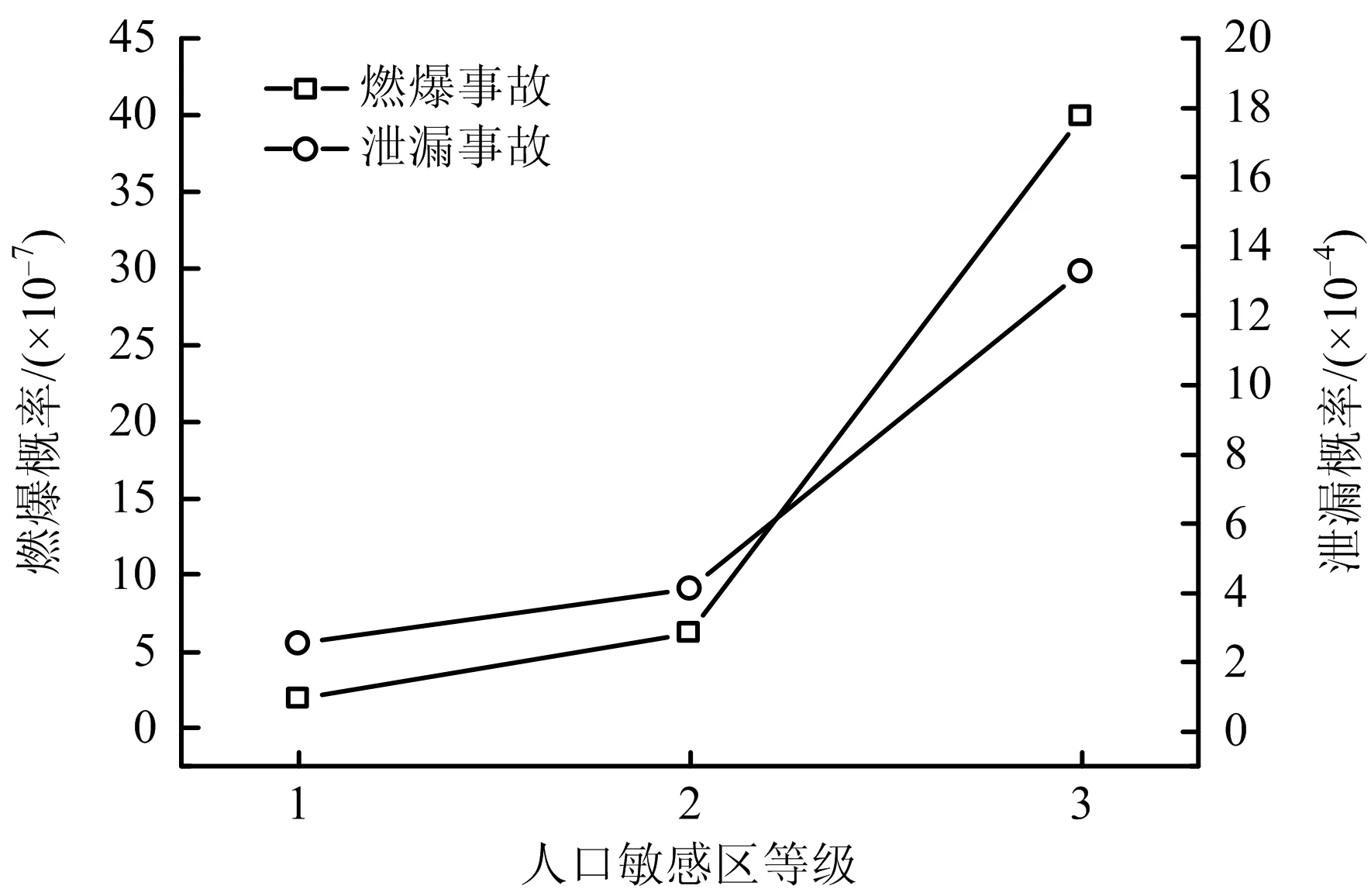
图5 不同等级人口敏感区泄漏燃爆事故概率对比

可以看出，随着地区人口敏感等级的提高，输气管道泄漏和燃爆事故发生的概率均随之增大，且燃爆事故发生的概率远小于泄漏事故发生的概率。

3.2 泄漏燃爆事故致因分析

3.2.1 基本事件后验概率分布分析

令P(N1)=1，通过贝叶斯网络进行反向推理计算，得到导致在3个等级人口敏感区发生输气管道燃爆事故的各根节点后验概率分布，见表7。输气管道泄漏燃爆各根节点后验概率分布对比如图6所示。

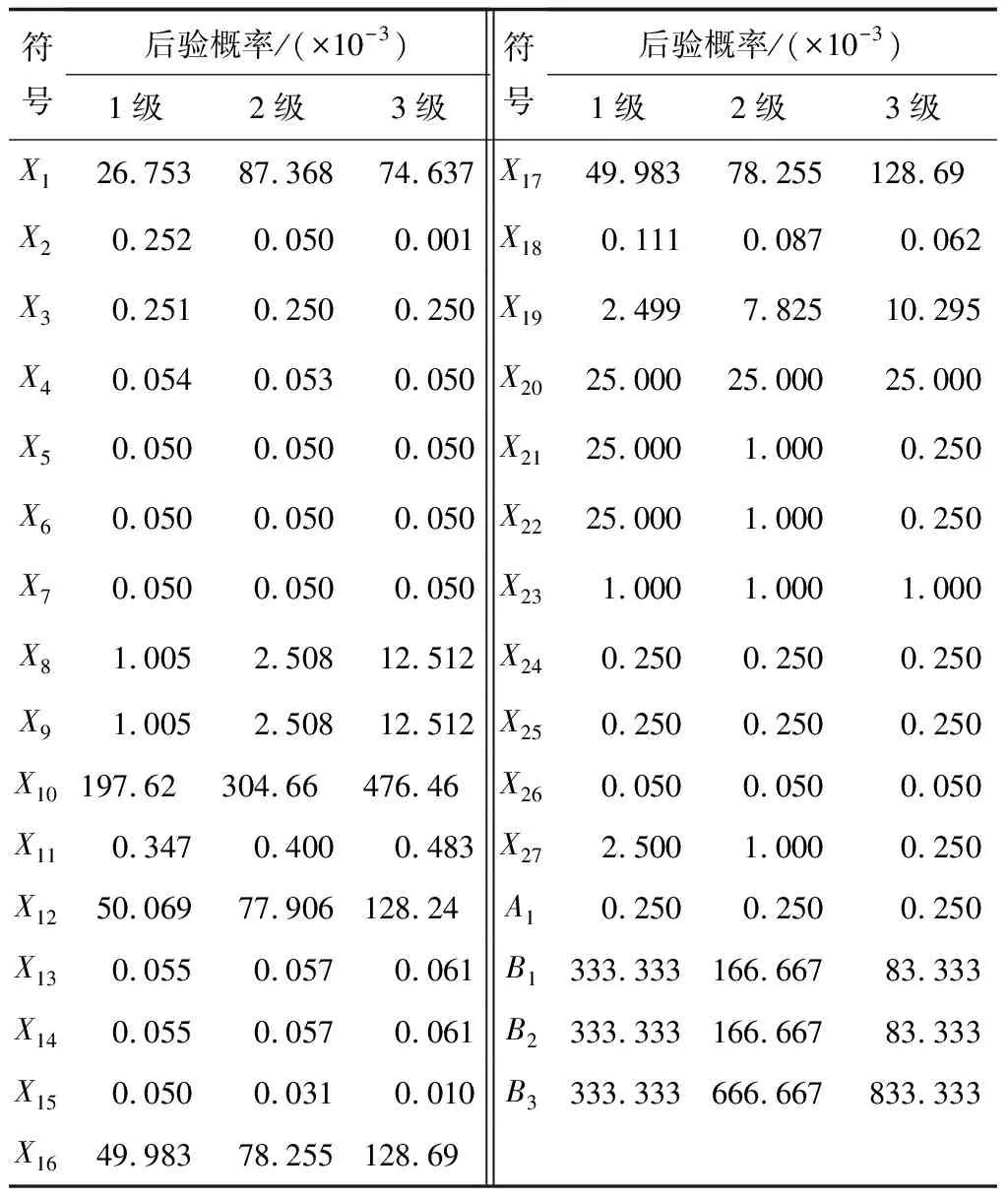
表7 根节点后验概率分布

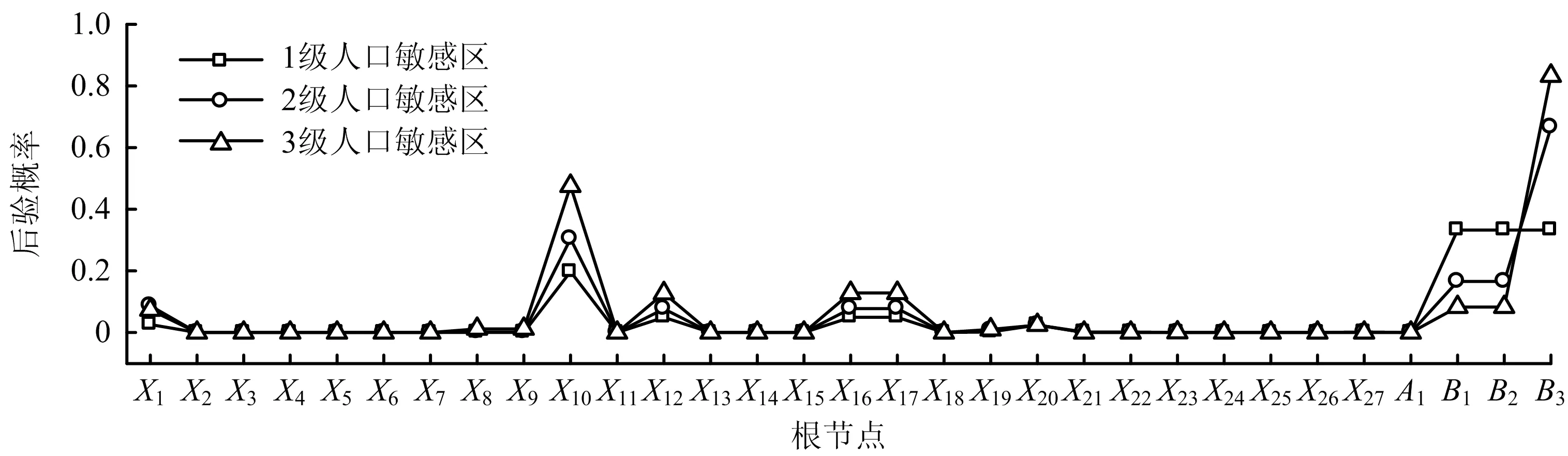
图6 输气管道泄漏燃爆各根节点后验概率分布对比

由图6可知：

1)不同等级人口敏感区中，相同根节点的后验概率存在差异。

2)在基本事件中，发生可能性最大的前几项为：X10,X12,X16,X17,X1。其中，X10,X12位居前2位，X10发生的可能性远大于其他基本事件。

3)在不同事故发生的触发条件中，变化最为明显的为B3，随着地区人口敏感等级的提高，远距离延迟点火发生的可能性增大。

3.2.2 灵敏性和影响力分析

为找出复杂致因结构中的重要参数以及导致事故发生的最可能途径[15]，对贝叶斯网络进行灵敏性和影响力分析。

1)灵敏度分析：3个等级人口敏感区的基本事件灵敏度大体一致，灵敏度较高的节点为X10,X12,X17,X16,X19,X15,X1，可以发现输气管道对非设计载荷较为敏感。

2)影响力分析：3个等级人口敏感区输气管道发生泄漏可能途径一致，可能性排序靠前的2条为：X12→Y12→Y5→Y2→T与X10→Y11→Y5→Y2→T。

3.2.3 小结

经后验概率分布、灵敏度、影响力分析，识别出风险性较大的基本事件为X10,X12，得到导致输气管道泄漏事故发生可能性最大的路线是由于施工破坏引起的管道泄漏，进而由远距离延迟点火导致燃爆事故发生。分析所得管道泄漏事故主要致因与EGIG对近40 a 1 366起管道事故分析所得结果基本相符，验证了所用方法的可行性。

4 结论

1)建立输气管道高后果区泄漏燃爆模糊Bow-tie模型并转化为贝叶斯网络，对不同等级人口敏感区泄漏燃爆事故易发性和事故致因进行分析。

2)随着地区人口敏感等级的提高，输气管道泄漏和燃爆事故发生的概率随之增大，燃爆事故发生的概率远小于泄漏事故；导致输气管道泄漏燃爆事故发生可能性最大的途径为：由于施工行为不规范和违章施工导致施工破坏，进而由远距离延迟点火导致燃爆事故发生。

3)在无输气管道高后果区失效数据的情况下，分析结果与EGIG对近40 a 1366起管道事故所分析的结果基本相符，这验证了该方法的可行性，但若有管道失效数据的支撑，可以采用统计所得概率与专家经验评判所得概率相结合的方法，计算得到的结果会更加精准。