基于MATLAB的指针式仪表识别的仿真设计

谢 伟，姜明明，张 刚，韩苗苗，玄 冉

（山东农业工程学院机械电子工程学院，山东 淄博 255000）

指针式仪表存在于生活的各个方面中，仪表的使用寿命是需要关注的问题。仪表每年都需要检修，检修步骤非常烦琐枯燥，检修工作量也非常大，而且对精度要求非常高，这无疑增加了工作难度。针对这一现象，笔者设计出一种基于MATLAB的指针式仪表示数识别系统，它可以高效、准确地识别仪表的数值，大大节省了人力，提高识别的准确性。

1 表盘定位与图像预处理

1.1 表盘定位

对于表盘定位来说，可以通过颜色来识别表盘，摄像头采集来的图片是RGB图像，RGB图像是由红（R）、绿（G）、蓝（B）三个分量组成。指针式仪表表盘背景为白色，仪表外壳为黑色，利用颜色分明这一特点来实现对仪表表盘的定位。对于彩色图像来说，在R、G、B三分量中，白色（R=G=B=255）对应的值都很大，通过设置阈值来判断白色区域。

1.2 图像预处理

图像预处理可以有效地突出表盘图像的有用信息，减少无用信息[1]，提高对表盘信息提取的准确性和识别率。又因为表盘简单，不需要太多的前期操作就能有效地识别出指针。所以只要进行图像灰度化、图像去噪等操作，就能优化对表盘指针的识别。

1.2.1 图像灰度化

图像灰度化目的是使计算机更好地识别图像，去除无用的颜色信息，保留线条和轮廓等有用信息，在RGB格式的图像中，利用公式：

由于R、G、B三个分量的取值范围是0~255，所以得出的灰度等级有256级，即能表现出256种灰度颜色[2]。

1.2.2 图像二值化

灰度化的图像经过处理后变成只有两个灰度级的图片，使后面的操作更加方便。但在实际操作过程中，会存在许多杂质，所以阈值的选择十分关键。在指针式仪表表盘上，黑白色彩明显，在选择阈值时，可以采用平均灰度值法，这种方法在对比度强的图片中十分有效，比较适合指针式仪表的二值化。二值化后的图像如图1所示。

图1 图像二值化

1.2.3图像细化

由于大多数指针式仪表的指针都很粗，在进行边缘检测和Hough变换时指针上会检测到两条直线，这样会使计算不精确，为了更好地进行指针识别，通常对图像进行细化。将图像的所有对象简化为线条而不改变图像本质结构的图像处理过程称为骨架化，对图像进行细化有助于突出形状特点以及减少冗余的信息量[3]。细化后的图像如图2所示。

图2 细化后图像

1.2.4 图像去噪

图像去噪能够减少图像中的噪声，可以采用以下两种方法。

第一种是采用中值滤波的方法。中值滤波是在该像素点本身以及周围像素点排列后，取它们的中值作为该点的灰度值，这种做法不仅方法简单，而且在消除图像噪声上效果比较显著。

第二种是采用局部均值滤波的方法。首先，找出图像数据中目标像素点以及周围八个像素点，然后对这九个像素点相加取平均值。得到的值就是计算后该目标像素点的灰度值。如果利用这种算法会使边界变得模糊，针对这一现象，可以选择对局部进行处理，如果目标对象局部存在边界，则不对其进行计算。

对图像进行上述处理后，发现局部均值滤波消除噪声的能力相对较弱，而中值滤波得到的图像清晰度高、细节处理好。所以本文采用中值滤波的方法进行去噪。

2 边缘检测

众所周知，对图像进行处理的目的有两个，第一个是使图像更能被人眼识别，第二个是使图像更能被计算机识别。而边缘检测就是为了使计算机能更好地识别图像。边缘检测是利用边缘检测算子获取图像中有用的信息，去除图像中的无用信息，以极少部分的有用信息，获取到更细节的部分，提高计算机分析图片的速度。常见的算子有Roberts算子、Sobel算子、Prewitt算子、Laplace算子和Canny算子[4]。这里以MATLAB为媒介，对各算子进行仪表表盘的仿真，以确定本研究采用的算子类型。对灰度化和去噪处理后的图像进行边缘检测后的结果，如图3所示。

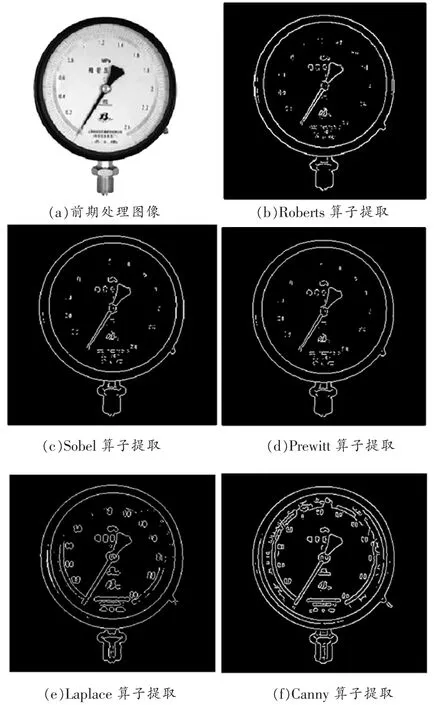
图3 边缘检测算子的MATLAB仿真比较

Roberts算子。Roberts算子的算法简单，运行速度快，对边缘定位的准确率较高。虽然Roberts算子对噪声影响明显，但前期的去噪处理，已经大大降低了噪声的影响。

Sobel算子。Sobel算子是常用的一阶微分算子，它是根据绝对值来取值的，这种方法对水平方向影响较大，不易确定边缘像素。但Sobel算子因其耗时短、具有一定的抗噪性、边缘检测效果较好而得到广泛应用[5]。

Prewitt算子。Prewitt算子也是一阶微分算子，它是加权平均算子，对图像处理有一定的限制，会破坏图像中的有用信息。而且利用此方法提取的图像不能连续表达，不利于指针的完整提取。

Laplace算子。Laplace算子是一个二阶算子，它对噪声的敏感性很高，对表盘提取的数据完整性高，而且基本无断点，但由于原始的Laplace算子在边缘检测方面还有诸多不足，一般不常用作边缘检测。

Canny算子。Canny算子具有较好的边缘检测能力，在图像处理方面运用十分广泛，而且边缘检测的结果更为细致，但会使仪表表盘中不重要的因素放大，而且方法复杂。

综合比较以上算法，由于采集来的仪表图片比较简洁，不需要用太过复杂的方法，综合各方面原因，采用Sobel算子进行边缘检测。

3 Hough变换与数值显示

3.1 Hough变换

在二维空间中，通常用y=ax+b的形式表示直线，a表示斜率，b表示截距。在MATLAB中，可以引用ρ、θ这两个参数来表示直线。

相应的直线方程如下：

ρ代表原点到该直线的距离，θ代表直线垂线与x轴夹角。

每一个直线方程对应一组（ρ，θ），直线上的每一点，都对应着ρ-θ坐标系中的一条曲线，取该条直线任意几点，这条直线所形成的所有曲线都会交于一点，这一点便是这条直线的（ρ，θ）值。如图4所示。

图4 共线坐标交于一点

把ρ-θ坐标进行网格化处理，在ρ、θ极值范围内，对其进行等分，以像素点为网格，利用交点累加器，每一条曲线上的点交于网格记为1，找出相交次数最多参数的点，就能找到对应x、y平面的直线线段，该线段就是仪表对应指针的位置。

3.2 数值计算

Hough变换检测直线，如果不做处理，所检测的角度范围是0°~180°，为了保证指针测量的精度，本文把ρ和θ的精度取为0.5。指针读数的关键在于指针与所建坐标x正半轴的角度，这个角度在Hough变换中是已知的，所以利用简单计算得到指针与右水平方向的夹角α，即如图5所示的角度。

图5 指针角度图

然后可以自行设置量程与指针式仪表的最大角度范围，根据量程和角度的换算关系，算出所得仪表的值。由于不同仪表所对应的量程和指针最大偏转角度是不同的，此设计主要适用于起始指针水平的仪表，如电流表、电压表、COSφ表等。使用时根据仪表种类只需更改界面中的仪表类型，系统就会自动跳转到对应的程序，最终计算出指针对应的数值。

3.3 GUI界面

利用GUI界面可以直观地得出计算结果，使得操作过程清晰易懂。通过此界面可以更方便地处理图像。按步骤依次操作，首先进行表盘区域识别，准确找到表盘区域，然后进行区域二值化、去除噪声、图像细化等操作，找到对应的仪表类型，最后利用指针与角度关系得出相应的数值。设置的GUI界面，如图6所示。

图6 GUI界面窗口

4 结语

笔者主要围绕指针式仪表的读数进行分析计算，通过MATLAB进行仿真，对大多数指针式仪表都适用，极大地提高了检修效率，降低了检修的工作量。

由于本设计是通过分析摄像头采集来的图片信息对图像进行处理，图像分析时对颜色有要求，所以采集图片时尽量在光照充足的地方进行。由于该设计是利用Hough变换进行的，所以倾斜角度不能过大，否则会对后续读数结果产生影响。