基于哈希和DNA编码的彩色图像混沌加密算法
袁 立, 谢 俐, 龙 颖, 胡春强, 蒋淘金
(1.重庆电力高等专科学校 信息工程学院,重庆 400053;2.重庆大学 大数据与软件学院,重庆 401331;3.重庆应用技术职业学院 电子信息与财经商务系,重庆 410520;4.重庆市公安局交巡警总队,重庆 400054)
混沌系统对初始值非常敏感,且具有良好的非收敛性和类随机性,因此在图像加密处理中具有广泛的应用[1-3]。当前,混沌系统在图像加密中的应用主要包括混合迭代结构加密、置乱加密、灰度替换加密等技术。文献[4]提出了一种流密码算法,它结合了一次一密和强混沌映射,基于分段线性混沌序列生成相应的密钥流序列,综合了混沌算法和循环加密的优势。1994年,DNA计算被Adleman首次提出[5],为图像加密处理提供了新的思路和方向。文献[6]综合Chebyshev映射和DNA计算的优势,将图像进行扩散加密,结果显示加密效果良好。文献[7]将DNA计算用于进行图像加密,使得猫映射在图像安全处理效果上有极大提升。以上算法只是单纯处理数字图像加密的算法,没有与处理文本的加密算法结合,存在一定的局限性。在文献[8]中,Abbas提出了一种基于Hash的数字图像加密算法,结果显示加密效果良好。
文中将哈希函数、Arnold混沌映射和Logistic混沌映射结合,对图像进行R、G、B3个维度的置乱;然后利用DNA编码对图像进行混乱处理。结合实验结果表明:文中图像加密算法具有很好的加密性。
1 算法基础
1.1 Logistic映射
Logistic映射模型比较经典,主要用于对动力系统、分形系统等复杂系统进行分析和研究。Logistic映射本质是一个在时间上离散的动力系统,其迭代公式为
xn+1=μxn(1-xn),
(1)
式中,μ∈(0,4),xn∈(0,1)。当3.569 945 6<μ≤4时,Logistic映射处于混沌状态。
将Logistic映射[9]改为
(2)
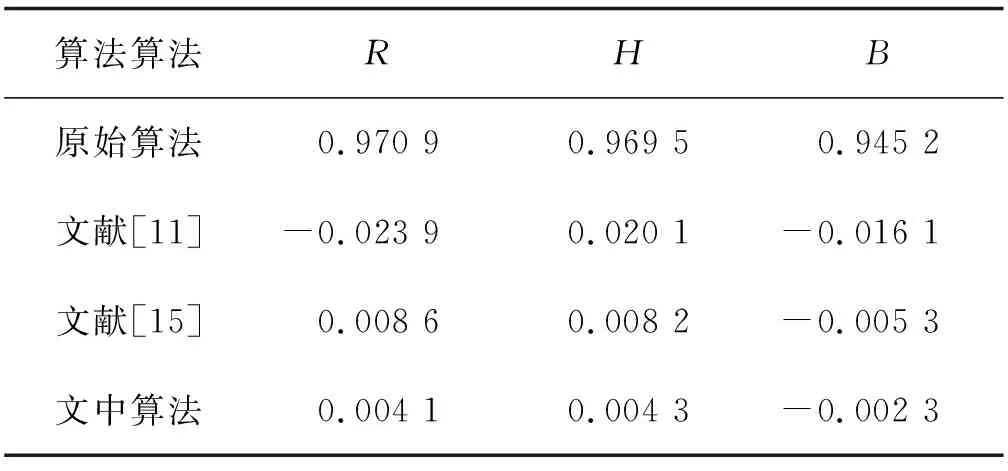
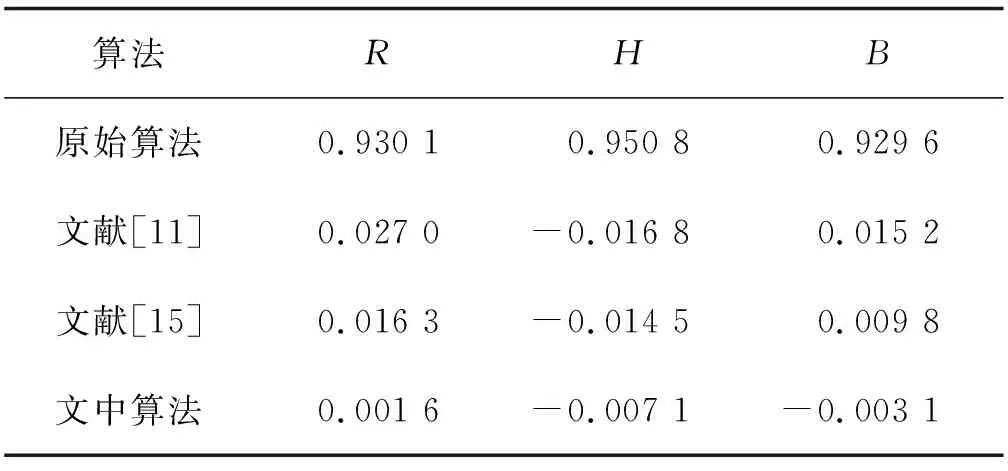
式中,xn为映射变量,0 俄国数学家Vladimir Igorevich Arnold首次提出了Arnold映射,又称猫映射。本质来说,Arnold映射就是在有限的区域内进行反复折叠和伸缩变换。 其原始公式为 (3) 对其进行数字化处理之后,得到映射关系为 (4) 式中,a、b、N均为正整数。 DNA序列由A、T、C、G 4个碱基组成,其中A和T、C和G存在互补关系。如果使用2 bit表示字节表示一个字母,那么DNA编码的方案共有4!种。但是满足碱基互补原则的只有8种,如表1所示。 表1 DNA序列的8种编码/解码规则 一套基于DNA序列的基本代数运算被King等[10]提出,其基本思想起源于二进制的加减法运算。DNA序列的基本代数运算与编码方案有很强的关系,不同编码方案对应的加减法规则也不同。以表1中第1种编码方案为例,其对应的加减运算规则如表2所示。 表2 第1种编码方案的加减运算 哈希函数又叫散列函数,它能够将不同长度的信息转换成一个固定长度的信息。SHA-256函数可以将图像信息转换成256位的哈希值。SHA-256函数对初始值极其敏感,图像内容有任何细微的差别,计算出来的哈希值都会发生巨大的变化。 为了使加密效果更好,充分利用SHA-256函数、Arnold混沌映射、改进Logistic混沌映射和DNA加密处理的优点,文中提出一种新型加密技术,其算法步骤如下: 步骤1:假设明文图像的尺寸为M×N,将其按照红、绿、蓝3个维度进行转换,得到3个平面分别为R、G、B。这3个平面尺寸均为M×N,每个像素的值均在(0,255)之间且为整数。若M和N值不相等,则可以通过补0的方式将其转换为N1×N1的方阵。 步骤2:分别求R、G、B3个平面的像素值之和,然后运用SHA-256函数分别计算这3个和值的哈希值,得到3组256位哈希值。式(4)的2个参数a、b和加密轮数N就是由SHA-256函数产生的3个参数值,分别作为R、G、B3个平面进行置乱处理的原始参数。 步骤3:运用按照式(4)分别对R、G、B3个平面进行置乱处理。 步骤4:将置乱后的R、G、B3个方阵进行二进制转换,每个平面转换后的大小均为N1×8N1,采用DNA编码规则对其进行编码处理,进而得到3个尺寸为N1×4N1的碱基方阵R1、G1、B1。 步骤5:按照式(2)进行混沌映射处理得到尺寸为N1×N1的混沌序列m,利用算子mod(floor(m*power(10,5)),256)将序列m进行整数化处理,得到相应的序列,采用DNA编码规则对数化处理后的序列进行相应的编码处理得到对应的矩阵。 步骤6:根据式(5)替换R、G、B3个平面的碱基序列,从而得到相应的3个平面R2、G2、B2。 (5) 步骤7:分别采用表1中的第4、2、7中的编码规则对置乱替换后的3个平面R2、G2、B2进行解码处理,得到相应的3个平面R3、G3、B3,尺寸为N1×N1。 步骤6:合成R3、G3、B33个平面得到相对应的密文图像,计算得到密文图像的和值,并将和值与密文图像进行异或运算,最终得到本文的加密图像。 加密和解密互为逆过程。解密是对加密进行逆运算,将DNA加法运算替换为减法运算,并按照R、G、B的逆序对进行恢复,即可解密图像。 文中选择明文图像为彩色的Lena图,尺寸为512×512,运行的环境为Intel Core i5 CPU@2.5GHz、8G内存、Win7 64位操作系统,仿真软件为MATLAB r2014a。对比图1中的3幅图分析可知,Lena图像经过文中加密算法处理后,已经看不到明文信息,说明文中提出的加密算法具有良好的效果。 图1 Lena图加密前后对比 若式(2)的初始值和迭代次数发生细微改变,会导致加密后的图像不能恢复成原始图像。例如,若在解密过程中,将式(2)的初值增加 1×10-15,则会导致图像解密失败,具体如图2所示。 图2 错误密钥的解密图 直方图能够体现出图像灰度值的分布情况。图像灰度值的分布情况能够体现出图像的抗攻击能力。若图像灰度值分布越平均,则其越能抵抗统计攻击[11-15]。从图3、图4、图5对比分析中可以看出:文中算法加密图像的直方图和文献[15]算法加密图像的3个分量直方图都是比较均匀的,说明都具有良好的统计攻击抵御能力。2个算法加密的图像直方图差别很小,加密效果接近。 图3 Lena图的R图像 图4 Lena图的G图像 图5 Lena图的B图像 为了验证文中算法的置乱效果,将基于水平、垂直和对角3个角度,从明文图像、加密图像中随机选取4 000对相邻像素点,然后运用式(6)~式(9)计算相邻像素间的相关性[15-20]。 (6) (7) (8) (9) 式中:x和y表示图像中两个相邻像素的灰度;N表示图像像素个数;E(x)表示x的数学期望;D(x)表示x的方差;cov(x,y)表示x,y的协方差;rxy表示相关系数。 若相关系数越接近0,则像素之间的相关程度越低,图像置乱效果越好,加密图像破译难度越大。从表3~表5可以看出,文中加密后的图像的相关系数更接近0,置乱效果更好。 表3 垂直像素相关性 表4 水平像素相关性 表5 对角像素相关性 为了更加直观地展现像素之间的相关性,选择B平面,分别从水平、垂直、对角3个方面进行像素相关性图像的绘制。图6和图7分别表示的是加密前和文中加密的线性关系。对比分析可以看出原始图像B平面3个方向的图像像素值集中在主对角线上,相关性很强,而加密图像像素值均匀分布,相关性很弱,可破解性更小。 图6 明文图像B平面相关性 图7 文中加密图像B平面相关性 信息熵体现了系统的随机性。图像直方图分布越均匀,则其随机性越强,信息熵就越大。式(10)所示的是信息熵的计算方式。对于灰度值范围为[0,255]的图像,其信息熵与8的逼近程度反映了抵御攻击的能力,信息熵越接近8,抵御统计攻击的能力越强。根据式(10)计算所得结果如表6所示。 表6 信息熵 可以看出,文中算法加密后的图像的信息熵更接近8,抗统计攻击的能力更强。 (10) 式(11)~式(12)分别表示的是NPCR(the number of pixels change rate)和UACI(the unified average changing intensity)这2项指标,此2项指标表示了图像的差分攻击抵抗能力。改变原始图像的R平面中(100,80)处的像素值,通过式(11)~式(12)计算出的NPCR和UACI的结果如表7所示。 表7 NPCR和UACI分析 (11) (12) 通过对比NPCR值和UACI值,可以看出文中算法抗差分攻击能力更强。 将均值和方差分别为0和0.05的高斯噪声加入到加密后的图像中。图8中,图8(a)表示的是加入高斯噪声后的加密图像,图8(b)表示的是相应的解密图像。可以看出:文中的加密算法在图像混入少量噪声后,仍然能够将其解密出来,抗干扰能力较好。 图8 抗干扰能力分析 随着网络技术的高速发展,彩色图像的安全性越来越受到重视。图像加密是一种很好保护图像信息的方法。文中结合哈希函数、Arnold混沌映射和Logistic混沌映射,使用DNA编码技术对图像进行混合加密。实验结果表明,本文的算法具有良好的加密效果,且对统计、差分攻击具有很好的抵御效果。1.2 Arnold映射
1.3 DNA序列编码
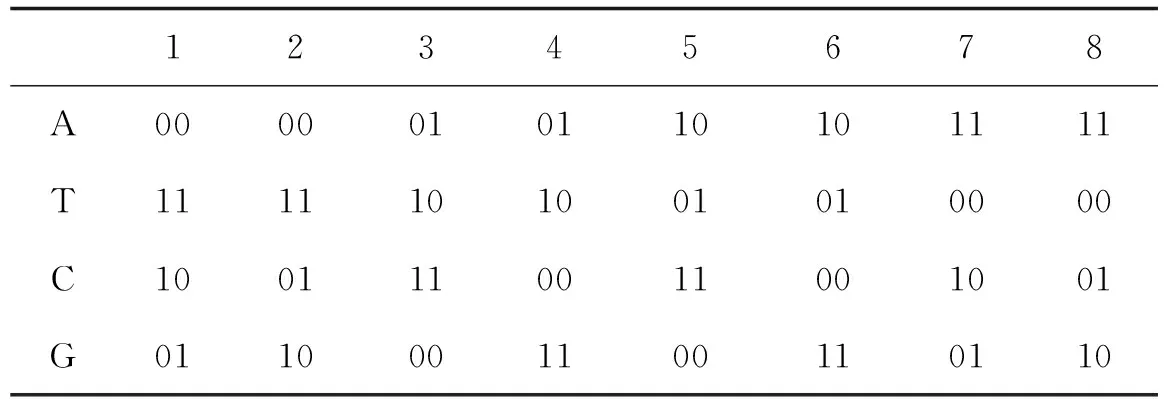
1.4 DNA序列的加法、减法
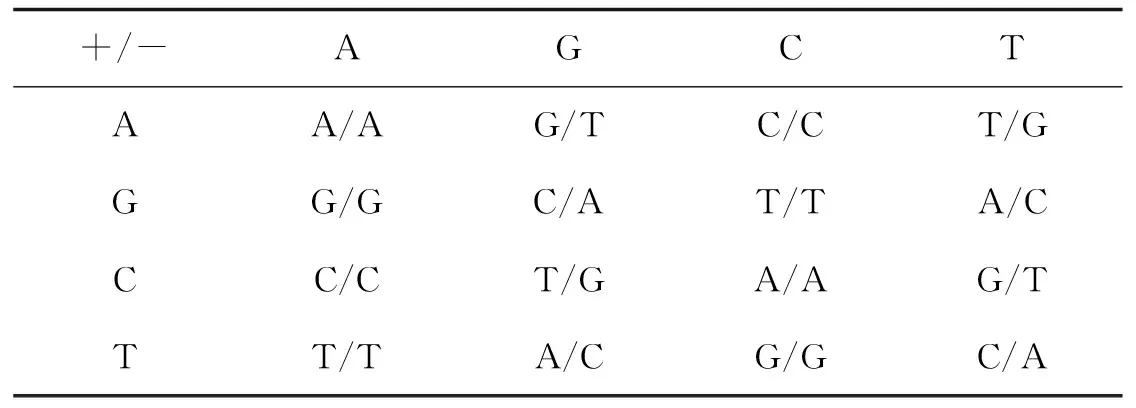
1.5 SHA-256
2 加密算法
2.1 加密算法
2.2 解密算法
3 实验结果分析

3.1 密钥敏感性分析

3.2 直方图分析

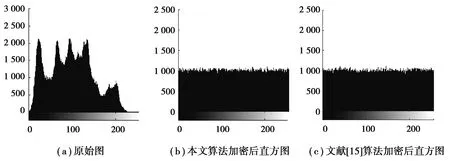

3.3 相邻像素相关性分析



3.4 信息熵分析

3.5 明文敏感性分析

3.6 抗干扰能力分析

4 结束语

