改进强化学习算法的UAV室内三维航迹规划

张 俊，朱庆伟，严俊杰，温 波

1.西安科技大学 测绘科学与技术学院，西安710054

2.西南大学 心理学部，重庆400715

无人机（Unmanned Aerial Vehicle，UAV）因其机动性能好、使用方便等特点，被广泛应用在各个领域。将无人机用于灾后室内环境搜索和救援时，可以降低对救援人员的伤害，提高任务效率，并能在救援团队无法到达的区域执行搜索任务。航迹规划是无人机自主导航技术的重要组成部分，其目的是找到一条安全且路径长度尽可能短的路径，供无人机从起始位置到达目标位置[1-2]。当发生灾害时，室内空间中分布着大量的障碍物，严重威胁无人机的飞行安全。因此，安全高效的航迹规划方法是无人机完成灾后室内环境搜索救援任务的关键。

目前，许多文献都提出了无人机航迹规划算法。在基于网格的搜索方法中，网格的每个单元代表无人机的一个飞行节点，可根据适当的搜索算法（例如Dijkstra算法）建立基于网格的路径规划方法[3-4]。文献[5]提出了一种解决加权连接定向网络的多准则最短路径问题的方法，将改良的粗Dijkstra标记算法用于确定最佳路径。在基于人工势场的方法中，根据接收来自目标和障碍物的吸引力和排斥力来改变机器人的路径。文献[6]根据分配给目标和障碍物的吸引力和排斥力，通过人工势场的强度得出潜在势场，提出了使用人工合成技术进行救援路径规划的方法。文献[7]使用一种基于A*和人工势场的混合路径规划算法，该算法对动态未知环境中的机器人进行路径规划。文献[8]提出了一种基于遗传算法和领航跟随法相结合的编队，在障碍物的环境下解决了收敛速度慢、路径不平滑的问题。文献[9]提出了一种结合模糊C均值（Fuzzy C-Means，FCM）算法的改进粒子群算法，用于三维环境中UAV的路径规划任务。文献[10]提出了一种在环境中针对完全指定目标的在线路径规划算法，并假设目标的位置和障碍物的信息是已知的。文献[11]提出了一种基于新兴技术的综合方法，通过无人飞行器和智能手机上的模拟信标的结合，就可获取检测到的失踪人员的GPS位置。然而，无人机进行灾后室内搜索和救援任务之前，障碍物的位置通常是未知的[12]，且目标位置和空间环境可能随时变化。在先前的常规方法中缺少必要的学习阶段，因此导致无人机的路径规划效率低。

针对上述航迹规划中存在的问题，本文基于现有强化学习算法，提出了一种用于无人机室内环境的航迹规划方法。在开始规划前，首先对室内空间环境进行离散化处理，以降低无人机路径规划的难度；再通过起点和终点间连线与障碍物位置关系，以确立主要障碍物及其环绕节点，舍弃与路径规划中不相关的障碍物和节点。随后，通过起终点坐标判断出目标点所在的方向，使无人机在初始阶段不再盲目选择节点，而是朝着目标方向搜索。最后，通过仿真实验验证了该方法的可行性。

1 空间离散化处理

当发生灾害时，室内空间环境中随机分布着大量的障碍物，由于空间环境处于连续状态，无人机在进行航迹规划时，很难顺利完成既定的搜索任务。因此，对室内环境进行空间离散化处理，从而在路径规划时可直接获得空间节点集，即在空间节点集中找到组成路径飞行的总成本代价最小的节点。

设每个节点knode代表无人机的一个三维坐标(xnode,ynode,znode)，令所有离散状态空间节点的集合设置为k，如式（1）所示：

对于无人机由起点到目标点飞过的路径节点构成的集合用G表示，如式（2）所示：

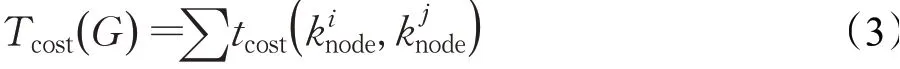
2 传统强化学习算法及不足

Q-learning是由Watkins提出的一种强化学习方法，为给定的马尔可夫决策过程提供最佳的动作选择策略[13-14]。通常，强化学习是在agent与环境之间交互循环中进行，如图1所示。在时间t中，agent观察到一个状态st∈S，执行一个动作at∈A，在这个过程中获得奖励rt∈R，随后时间索引递增，环境将agent传播到新的状态st+1，该状态下重新开始循环。最佳路径规划中agent的目标是最大化获得的总奖励，考虑折扣系数，可以将收到的总奖励定义如下：

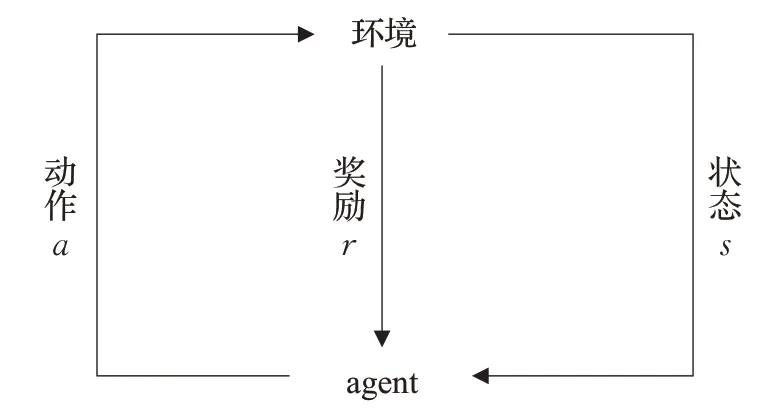
图1 强化学习的基本模型Fig.1 Basic model of reinforcement learning

其中，rt为时间t中获得的奖励。

通过不断的训练，agent可以自动感知未知的环境并最终获得具有最大累积奖励的状态动作集，对Q函数进行迭代改进的Q学习更新规则：

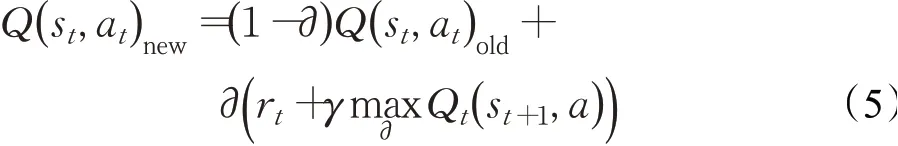
其中，st和st+1是在时刻t和t+1处的观测状态s,rt是在时刻t的收益矩阵R，并且Qnew和Qold分别代表更新后的Q表和更新前的Q表；学习率∂∈[0,1)决定将旧信息扩展到何种程度，折扣系数γ∈[0,1)平衡短期和长期奖励的重要性。γ接近1将使主体专注于获得长期奖励，而选择γ=0将使其仅考虑行为的立即奖励，γ=1可能导致动作值发散。在遵循每个状态-动作对被访问无数次且学习参数∂适当降低的假设下，无论遵循何种探索策略，Q学习都将收敛到最优策略。图2描述了传统Q学习的过程。

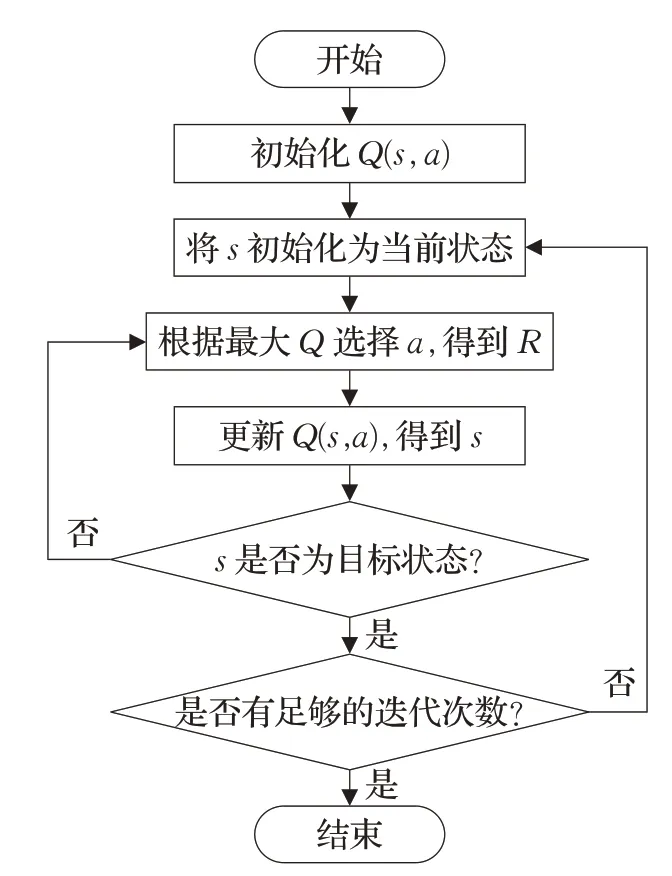
图2 算法流程图Fig.2 Algorithm flow chart

然而传统Q-learning无法直接用于航径规划。在一个具有m个状态和n个可能动作的环境中，构造出的Q表维数将为m×n。当从当前状态转换到下一个状态时，agent必须从n个可能动作中选择具有最高Q值的动作，这意味着需要n-1次比较。为了用n个状态更新Q表，所需的比较次数为m(n-1)。因此，当环境的大小和复杂度增长，尤其是在现实世界中，随着搜索空间的增加，完成路径规划的Q学习成倍增加[15]。

此外，在探索的初始阶段，由于Q值初始化为0，无人机的动作完全随机，导致不必要的计算，收敛速度慢且耗时，下一个状态选择的动作将由最高Q值确定[16-19]。

3 优化策略

为了克服上文中的局限性，对经典强化学习进行了优化，以满足无人机灾后室内环境的搜索和救援任务。首先，在算法学习之前，通过起点和终点间连线与障碍物碰撞确立关键的障碍物及包围障碍物的节点，舍弃与路径规划中不相关的障碍物和节点；然后，用给定的起点和终点坐标求出目标点相对于无人机的方向，使无人机在初始阶段不再随机进行选择，而是朝着目标方向搜索，从而降低了空间复杂性和提高了收敛速度。

3.1 空间优化策略

基于起点s和终点g的连线内与障碍物所处的位置关系，首先判断出一组主要障碍物MO，并找到一组MO周围的障碍物环绕点SP，以此达到限制MO的目的。然后，由起点和终点经SP上的网格点到达目标点，生成飞行路径，如图3所示，其中实心小球为选择出的主要障碍物围绕节点，空心小球为栅格节点。具体步骤为：基于与sg的碰撞，从一组危险因素中识别出一组主要障碍物MO和次要障碍物NMO，障碍物定义为O，其中MO⋃NMO=O且MO⋂NMO=∅。然后令h作为基于两个输入之间存在交集和并集的判断函数。若返回为1，则为MO，否则为NMO，可用以下方程式定义MO和NMO。

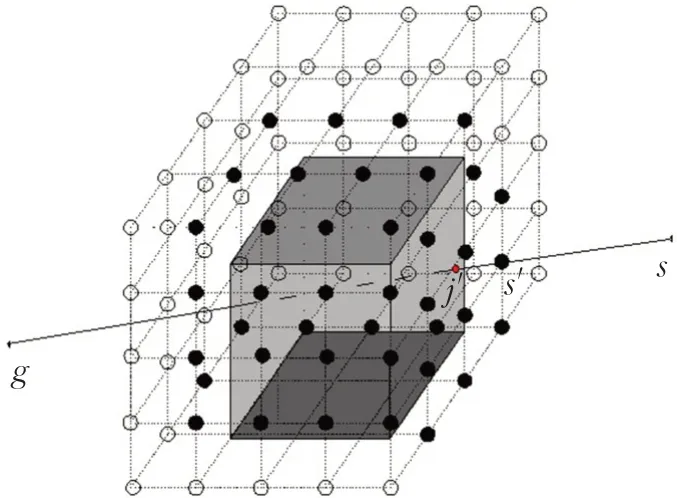
图3 三维环境中MO-SOP过程Fig.3 MO-SOP process in a three-dimensional environment

确定了航迹规划中的主要障碍物MO后，判断出可行节点k的子集SP，以确定围绕MO的一组节点。围绕oi∈MO的一组点表示为spi，确定spi是基于某个参考点c，其相邻点是距离参考点3d（d为栅格步长）长度的节点，由这些相邻点可构成一个多维数据集。如果满足式（8）的点定义为可行相邻点，将其存入点集N()

c中，如式（8）所示：

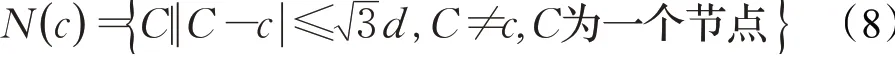
N(c)是一个等待列表，其中包含选作为SP的参考点。若oi与参考点c的多维数据集ci相交，则返回1，否则返回0，表达式为由于spi中的所有点都是c的多维数据集与oi相交并从临时列表中移除得到的，可得出spi⊂kh，当spi是一组围绕oi的节点时，则spi=kh；而如果在进行SP进程找到周围所有点前就结束了，表明spi≠kh，则c不会确定为spi的元素，因为它与oi的距离还不够近，无法有效地围绕障碍物。因此，c的相邻点也将被忽略且不会输入到该集中。重复此过程直到该集变为空集，即可获得围绕oi的网格点的子集。

初始参考点c可以通过s′获得，即oi的SP过程的起点，这样可以使参考点成为可行的节点，便于对oi启动SP过程。定义s′之前，首先确定oi∈O和sg之间有n个相交点{ }jd1,jd2,…,jdn，距离s最近的相交点定义为j′,j′定义如式（9）所示：

然后根据j′来处理s′，从而开始进行针对oi的SP处理，如式（10）所示，表示在s和j′之间的所有节点中，距离j′最近的节点

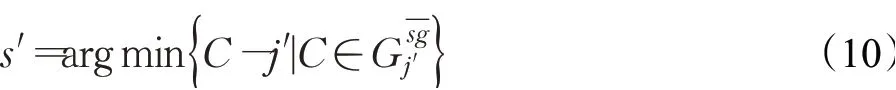
找到MO中所有障碍物的周围点集之后，即可规划出从s到g的航迹，所规划出的航迹是基于图形T=(V,E)生成的，其中V是一组顶点，E是一组连接顶点对的边。

除了提高无人机三维路径规划的效率外，本文所提的优化策略在降低路径长度方面也具有优势。在优化方法中，进行无人机三维路径规划时只考虑某几个障碍物，其中每个顶点连接到一定数量的顶点或最近的相邻节点，而不是整个图形。因此，在将图的密度定义为有限数量的连接点的情况下，空间中的点数量的减少有利于缩短路径长度。

3.2 Q值初始化策略

Q-learning是一种“试错”算法，收敛速度慢是Qlearning算法的一个重要缺陷。

无人机在三维环境中可向除自身外的26个方向之一运动，在路径探索初期，由于Q值初始化为0，无人机将向其周围的相邻点随机移动，收敛速度慢同时耗时较长。因此通过确定相对于起点位置的目标方向，对Q值进行初始化，使得学习初期即有一定的目标性。无人机飞行方向与起点和终点连线的夹角越小，构造的方向趋向函数值越大，就能获得较高的奖励，无人机将跳过向其他方向的移动，并且从开始位置到目标位置的整个移动过程都会重复这种状态，此过程将引导无人机朝着目标方向搜索，减少计算路径和到达目的地的时间。

通过以下关系确定当前无人机目标点的方向：将无人机起点坐标定义为s(sx,sy,sz),目标点定义为g(gx,gy,gz),下一个待选节点坐标定义为n(nx,ny,nz)。首先，通过待选节点坐标和终点坐标分别减去起点坐标，确定待选节点和终点与起点之间的差值，即：

然后如图4所示，令θ为向量sg和向量sn之间的夹角，其余弦值为：

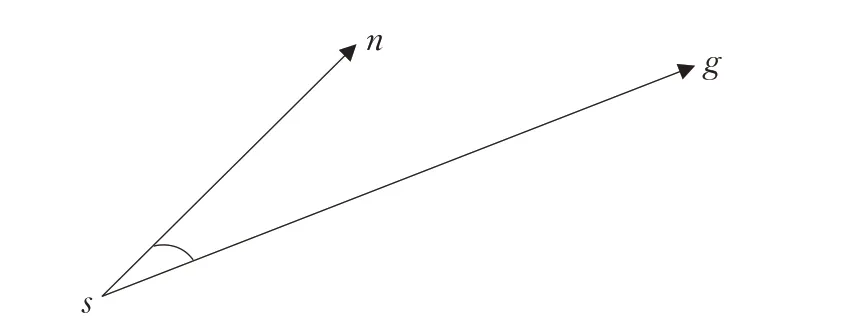
图4 起点与待选节点直线和目标点直线之间的夹角Fig.4 Angle between starting point and straight line of selected node and straight line of target point

式（12）中两个向量夹角值越小，余弦值越大，表明无人机动作方向靠近目标方向，能获得更大的奖励，于是构造方向趋向函数：

其中，q为方向趋向因子，D为当前待选节点到目标状态的欧式距离在Q值初始化过程中，利用si处的方向函数值来初始化状态价值函数V(si)，并通过式（14）行为价值函数和状态价值函数之间的关系来实现Q值的初始化，即：

4 算法实现步骤与实验

4.1 算法步骤

结合了目标方向和MO-SP策略的灾后室内无人机强化学习航迹规划策略的实施过程如下：

步骤1已知起点和终点坐标的条件下，根据起点和终点连线位置关系，确定所连直线经过的主要障碍物，判断主要障碍物周围的节点相对于障碍物的位置关系，当时，则为环绕主要障碍物的节点。

步骤2在初始状态下，根据起点和终点的位置确定目标点所在方向，实现对环境先验信息的初始化。

步骤3利用环境状态值函数更新Q(s,a)。

步骤4无人机采取可变贪心法则，每移动一步就更新一组Q()s,a，直到搜索到目标点，再进行多次迭代达到稳定的收敛值。

4.2 实验结果与分析

为了验证本文优化的强化学习方法在路径规划中的有效性，在三维栅格地图中对所优化的强化学习算法进行实验。在本实验中，考虑一架无人机、一个目标点，并且考虑无人机可向任意方向移动。本实验栅格地图尺度为90×60×50栅格，实验搭建的三维模型如图5所示，为了更接近真实室内环境，环境中随机设置障碍物。无人机的起始位置为（6，54，0），目标点的位置为（78，30，18），将目标点设置在远离边界的位置，以防止某些实验性事故的发生。

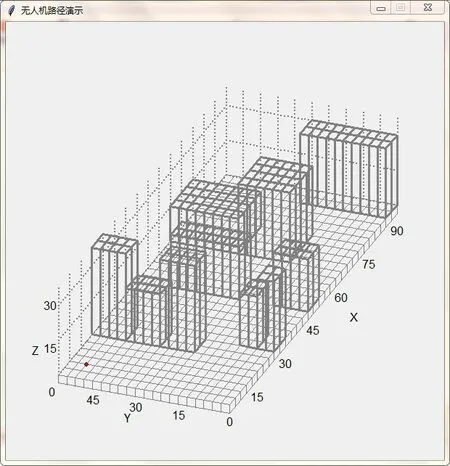
图5 三维环境模型Fig.5 Three-dimensional environment model

算法中相关参数设置如下：算法最大迭代次数max_iteration=1 500,学习率∂=0.1，折扣因子γ=0.96,贪婪度ε设置为0.8；设置回报函数Rt=100，对于即时奖励r值的设置，可通过以下式子：

其中，δ、τ是参数，本实验中设置δ为10，设置τ为40；dt为当前状态与目标点之间的距离，dt+1为下一个无人机位置到目标点的距离，d0为无人机与障碍物之间的距离。

4.2.1算法有效性验证

为了评估所提出算法的性能，评估了在每个情节中找到目标的收敛时间、路径长度等评价因素，并对获得的结果进行了比较和讨论。在这项研究中，进行了三组实验，分别是经典Q学习算法，记为C-Q算法，引入目标方向的Q学习算法，记为T-Q算法，以及基于目标方向和MO-SP的综合改进Q学习算法，记为A-Q算法。为了消除随机误差对结果的影响，每种算法在实验环境中多次运行后取切尾均值，然后将三种算法的结果进行比较以验证算法的有效性。每种算法达到目标所规划的路径和算法的收敛情况分别显示在图6和图7中，结果记录在表1中。

图6 三种Q-learning算法的路径图Fig.6 Path diagram of three Q-learning algorithms

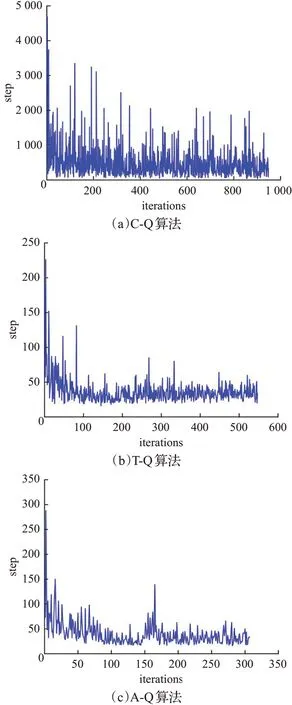
图7 三种Q-learning算法的收敛情况Fig.7 Convergence of three Q-learning algorithms

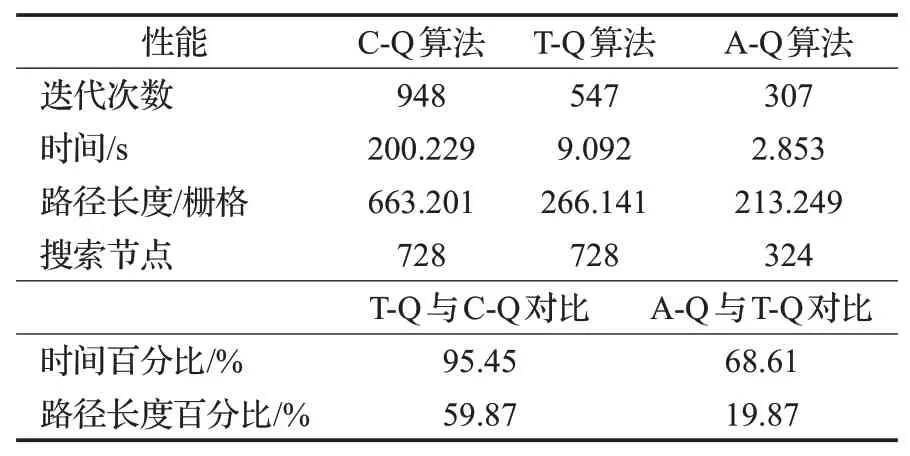
表1 三种Q-learning算法的性能比较Table 1 Performance comparison of three Q-learning algorithms

由图7（a）可知，C-Q算法经过948次的迭代才收敛到目标点，但在学习初期，无人机需要超过4 000次的尝试才能找到到达目标位置的路径。这是因为算法的初始阶段，Q值初始化为0，使得没有经验的无人机只能随机选取动作，从而使算法的收敛速度很慢。图7（b）是在C-Q算法基础上计入了目标方向策略的T-Q算法，通过仿真结果可知，T-Q算法在经过547次迭代收敛于目标。在学习初期，找到目标位置的路径所需要的尝试次数为252次，远低于C-Q算法；同时，算法从起始位置到目标方向的收敛时间相比于C-Q算法减少95.45%，这是因为Q值初始化时无人机就有一个朝着目标的方向，从而避免搜索与无人机终点方向无关的节点，减少了额外的时间开销；由于减少了不必要方向的搜索，T-Q算法所得的路径长度比C-Q算法降低了59.87%，且从图6可知，T-Q算法的搜索路径图比C-Q算法更符合任务要求。上述分析表明引入方向目标策略能够在学习初期引导无人机快速收敛，并缩短学习时间和路径长度，从而提高收敛速度。由图7（c）可知，在学习初始阶段，无人机到达目标位置的尝试次数较T-Q算法有略微的增加，但A-Q算法在经过307次的迭代后就能收敛于目标点。与图7（b）仿真结果比较可知，在目标方向的基础上，对环境进行MO-SP策略，使算法的收敛时间较T-Q算法减少了68.61%，空间搜索节点减少了55.49%，同时路径长度也得到了进一步的减少。集成后的算法能更进一步提高算法初始阶段的学习效率，改善无人机路径规划强化学习算法的性能。

4.2.2算法适应性验证

为了确定本文优化算法的适应性，在不同的起始位置点和障碍物中进行了三组实验，设置每组实验的目标点坐标均为（84，30，18），每次实验运行多次并取结果的切尾均值。图8显示了三组实验的路径规划图。其中地图a与地图b为相同起点和终点条件下不同障碍物环境，地图a与地图c障碍物位置相同而起点位置不同，结果比较见表2。根据表2结果可知，本文优化的Q-learning算法在不同场景中具有良好的适应性。

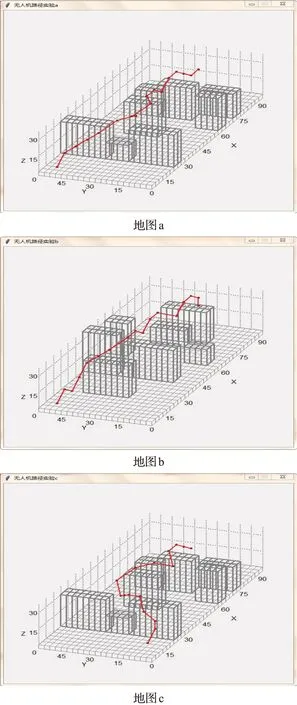
图8 不同环境中优化Q-learning航迹规划图Fig.8 Optimized Q-learning trajectory planning diagram in different environments

表2 不同环境中优化Q-learning的性能比较Table 2 Performance comparison of optimized Q-learning in different environments

5 结束语

传统强化学习Q-learning算法在初期，由于缺乏先验知识，收敛速度慢，同时三维环境中空间复杂度高，对路径规划具有很大的影响，无法直接用于灾后室内环境中的搜索和救援任务。本文提出了一种优化型强化学习Q-learning算法，通过起点和终点的位置关系确定出三维栅格地图中路径规划的主要障碍物及障碍物包围的点集，并且通过数学关系确定目标所在的方向来初始化Q值。仿真结果表明：相较于传统Q-learning算法，在初始化Q值的过程中确定目标所在方向，能有效降低算法的收敛时间；目标方向和MO-SP策略整合后算法收敛时间降低了98.57%，搜索节点数量降低了55.49%；所规划的路径长度也得到了明显的缩短。本文仅考虑静态路径规划，因此将本文所提的优化型Q-learning应用于涉及动态移动障碍的路径规划是未来进一步研究的方向。