基于曲波噪声估计的K-SVD字典学习地震资料去噪
杨熙镭,刘怀山,2
(1.中国海洋大学 海底科学与探测技术教育部重点实验室,山东 青岛 266100;2.海洋国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266071)
1 引 言
地震资料去噪一直是地震资料处理的一个重要环节,去噪结果的好坏直接影响到地震资料处理整个流程。受限于地震数据采集过程中野外条件以及设备成本的限制,实际采集到的地震资料中经常存在大量的随机噪声。低信噪比的地震资料会给后期处理环节的速度分析、偏移成像等带来困难,影响地震资料成像的可靠性。因此地震资料去噪是提高成像分辨率的重要手段,是后续地震资料处理流程高质量进行的基础。
在实际地震资料中往往无法直接获得随机噪声的先验参数,而本文旨在利用曲波变换得到地震资料的噪声估计作为先验信息,自适应选择合适的随机噪声标准差得到K-SVD字典学习重构的误差参数,从而实现在无人为设定参数的情况下,通过K-SVD字典学习方法实现对随机噪声的压制,提高地震资料的信噪比。
2 方法原理
2.1 K-SVD字典学习算法
K-SVD字典学习的方法是通过从已知的信号中获得训练样本集,在稀疏约束的条件下不断训练学习,对信号特征值进行提取,实现信号的最大稀疏化,并获得经过训练后的超完备字典和稀疏系数[17]。K-SVD算法的主要数学思想是利用一个包含K个原子dk的字典矩阵D∈Rm×K,来最大化稀疏线性表示原始信号Y∈Rm×n,y∈RM×1对应二维信号中的列向量,称为训练原子,则有Y近似于Y1=DX,其中m、n分别对应二维信号的行列数,X∈RK×n为稀疏系数矩阵,xi(i=1,2,…,K)为该矩阵中的行向量,这样就转化为了如下的优化问题
(1)

(2)
其中,
(3)
此时(1)式的优化问题可以转化为
(4)
(5)
(6)
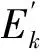
在坡度小于15°区域内,农村居民点斑块面积与数量占比高达91.9%与86.8%。在小于5°区域农村居民点密度、平均面积与标准差高出其他区域较多,而5°~15°区域内斑块数量与景观形状指数大于0°~5°区域,体现出0°~5°区域内农村居民点具有连片聚集大规模的特征,而5°~15°区域内农村居民点斑块更加碎小、并具有离散分布特性。随着坡度增大农村居民点总面积、面积比例、数量等各项指数均减小,且在坡度大于25°时降至极低水平,表明坡度对农村居民点分布与规模均具有极大的影响。农村居民点形状指数在0°~5°区域内最高,表明区域内农村居民点形状复杂,而其他区域差异不明显。
2.2 基于曲波噪声估计的K-SVD字典学习去噪方法
K-SVD字典学习去噪是通过选取一部分含噪的地震资料作为样本进行学习,获得一个与该地震资料相适应的超完备字典,其中地震波有效信号在该字典内能够稀疏表示,而地震资料中含有的随机噪声则是在整个稀疏域均匀分布,通过重构算法便能够实现有效信号和随机噪声的分离。为了在实现较好的随机噪声压制效果的同时,能够最大程度地保留有效信号不被切除,需要合理设置重构算法的误差参数。目前大部分主流的重构算法,例如正交匹配追踪(OMP,Orthogonal Matching Pursuit)、分段正交匹配追踪(StOMP,Stagewise Orthogonal Matching Pursuit)等,都需要获取随机噪声的先验信息来控制误差参数,才能实现较好的去噪效果,但在实际地震资料处理中,无法直接获取数据中随机噪声的先验参数,只能通过不断地调试输入的误差参数来控制去噪效果。本文将曲波变换中所利用到的曲波噪声估计[22]单独提取出来作为一个模块来获取地震资料的噪声先验信息。由于曲波变换的性质,不同方向上的曲波系数能够表征图像在该方向上的特征信息,从而能够帮助人们在曲波域内获得噪声方向,实现在曲波域的噪声估计。
曲波噪声估计是对地震资料进行曲波变换,即
(7)
其中C表示曲波系数,j为尺度参数,l为方向参数,k为位置参数,f为含噪地震资料,φj,l,k是在曲波变换的基函数。根据已获取的含噪地震资料的曲波系数,选取其中某位置k的的曲波系数矩阵,选择其中尺度参数j最大的一系列曲波系数。设Egj,l为含噪图像在j个尺度第l个方向上投影得到的平均能量,Efj,l为原始图像在第j个尺度第l个方向上投影得到的平均能量,Eηj,l为图像噪声在第j个尺度第l个方向上投影得到的平均能量,其中

Efj,lmin≤Efj,l
(10)
(11)
说明在lmin方向随机噪声能量最大,可以在此方向上获得更好的噪声估计。所以地震资料经曲波变换后,选取某点曲波系数中尺度参数最大且符合lmin条件的,则该曲波系数对应该点的最佳噪声估计,并通过曲波系数得到相应的随机噪声标准差,再依此获得地震资料中每一点的随机噪声标准差,并通过求取所有这些点随机噪声标准差的平均值,获得整个地震资料的随机噪声标准差。
因此基于曲波噪声估计的K-SVD字典学习去噪的基本流程步骤是:
1)对含有随机噪声的地震数据进行曲波变换,在曲波域利用曲波分解系数进行噪声估计,即通过获得符合最优噪声估计的曲波分解系数确定随机噪声标准差;
2)选取部分地震数据作为字典学习的训练样本集,利用OMP算法得到这部分地震资料的稀疏表示,获得稀疏矩阵;
3)利用K-SVD字典学习方法对稀疏矩阵和字典进行迭代更新,获得适应该地震资料的超完备字典及其对应的稀疏矩阵;
4)利用步骤3)中获得字典和稀疏矩阵,通过OMP算法重构地震资料,在重构过程中,通过步骤1)中获得的随机噪声标准差控制重构的迭代参数,最终重构出去噪后的地震资料。
3 模拟数据测试
为检验本方法对地震资料中随机噪声的去除效果,模拟单炮地震记录,假设简单的四层水平均匀介质,以主频为45 Hz的Rick子波作为地震子波进行激发,实现中间激发两端接收,得到512道地震数据,单道采样点数为512个,采样间隔为0.001 s,得到模拟地震记录如图1(a)所示,加入标准差为4的高斯随机白噪声,得到含噪模拟地震记录如图1(b)所示。本文图件纵横端点所标注的数值,均为端点处刻度所对应的数值。

图1 模拟地震记录加噪前后对比Fig.1 Comparison of simulated seismic records before and after noise addition
分别对含噪模拟地震记录(高斯随机噪声标准差为4)使用中值滤波、维纳滤波、小波变换、本文方法进行去噪处理,并获得去噪后残差剖面。其中本文方法通过曲波噪声估计得到含噪模拟地震记录的噪声标准差估计为3.9。设定基本字典参数,包括字典分块大小为8,余度系数为4。
图2展示了应用这四种去噪方法得到的地震记录以及对应的残差剖面。图2纵坐标为时间,横坐标为道号(CDP号)。从图中可以看出,中值滤波去噪方法虽然有效地压制了随机噪声,恢复了反射波同相轴,但是通过残差剖面可以清晰地看到部分有效信息也被切除;维纳滤波去噪方法相较于中值滤波更好地压制了随机噪声,但是通过残差剖面图像可以看出部分有效信息也被切除,而且应用中值滤波去噪方法和维纳滤波去噪方法后所获得地震记录中反射波同相轴并不光滑,依然存在噪点;应用小波变换去噪方法后,有效地压制了随机噪声,较好地保留了有效信号,反射波同相轴更为光滑,但是可以看到其对随机噪声的压制效果不及维纳滤波,去噪后地震记录的部分区域仍可见噪点;采用本文方法进行去噪后,同相轴光滑,有效信息得到保留,随机噪声压制效果较好。
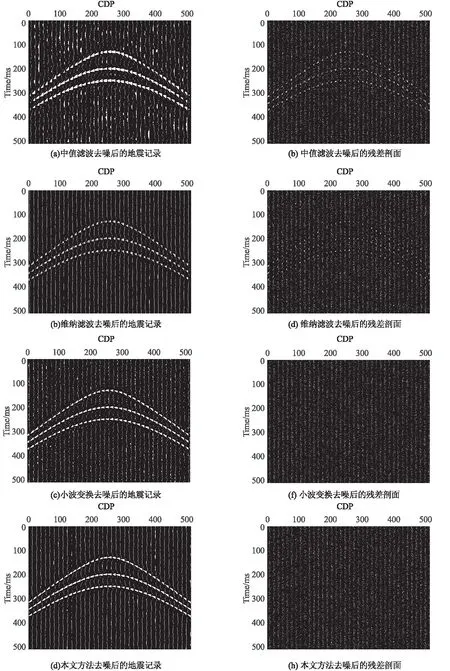
图2 去噪后的地震记录及其对应的残差剖面Fig.2 Seismic records and their corresponding residual profiles after denoising
为了更清晰地对比本文方法与小波变换的去噪效果,提取第250道的单道地震记录进行对比,如图3所示,可以看到本文方法对比小波变换去噪方法,压制随机噪声的同时,能更好地还原有效信号的幅值,避免了小波变换后幅值出现增益的情况。

图3 第250道单道地震记录去噪前后对比Fig.3 Comparison before and after denoising of the 250 th single channel seismic record
为了定量分析应用各个方法后的去噪效果,本文采用信号的信噪比(SNR,Signal to Noise Ratio)和峰值信噪比(PSNR,Peak Signal to Noise Ratio)作为衡量标准,其中二维信号的SNR和PSNR分别定义为
(12)
(13)

(14)
表1为对含噪模拟地震记录应用不同去噪方法效果的比较。从表1中可以知道对于同样的含噪地震资料,采用各种去噪方法压制随机噪声后,信噪比均有所提升,但是通过对比可知,利用本文去噪方法进行处理后的SNR和PSNR最大,说明本文方法的去噪效果优于其他几种方法。

表1 几种不同去噪方法的效果比较
4 实际资料测试
为了验证本文方法在实际地震资料去噪中的效果,对某海域含噪拖缆地震资料的叠加剖面进行去噪,实际地震资料如图4所示。分别利用中值滤波、维纳滤波、小波变换以及本文方法这四种方式对实际地震资料进行去噪处理,得到图5所示的实际地震资料去噪效果对比图。图4和图5的纵坐标为时间,横坐标为道号(CDP号)。其中本文方法采用同模拟数据测试部分相同的参数设置。

图4 实际含噪地震资料Fig.4 Actual seismic data with noise
从图5中可以看出,中值滤波去噪处理后,同相轴基本已不再连续,无法识别出实际地震资料中原本存在的断层构造;维纳滤波去噪后,虽然在浅部的强反射界面得到了较为连续的同相轴,但是其余深部的同相轴均在去噪过程中被切除,导致有效信号大量损失;小波变换去噪后,得到了大部分有效信号的同相轴信息,且可以明显依据去噪后的信息推断出实际资料中存在的断层构造,但是其去噪后所得反射波同相轴仍然存在部分不连续的位置;本文方法去噪处理后,同样恢复出大部分反射波同相轴,并且浅部强反射界面的同相轴连续性和光滑程度都要比小波变换去噪处理后更好。
结合图4和图5可以看出,本文运用的所有去噪方法,均导致650 ms下方两个弱反射同相轴被压制,说明运用包括本文方法在内的各种方式进行去噪处理后,都会不同程度地对反射波同相轴产生影响,但是相较于传统方法,本文方法最大限度地降低了对有效信号的干扰。同时也说明在面对具有较低信噪比的地震数据时,本文方法也存在一定的局限性,虽然能够准确地估计随机噪声,但是当噪声幅值与弱反射同相轴的幅值过于接近时,进行去噪处理后仍无法有效保证弱反射同相轴的连续性。

图5 实际地震记录去噪前后对比Fig.5 Comparison of actual seismic records before and after denoising
5 结 论
本文提出基于曲波噪声估计的K-SVD字典学习去噪方法,能够直接对需要去噪的地震资料进行噪声估计,使得K-SVD字典学习去噪方法不仅能够自适应地基于地震资料获取超完备字典用于重构,同时能够自适应地获得该地震资料的随机噪声标准差,增强了K-SVD字典学习去噪的泛化能力。对模拟资料和实际数据的测试均表明该方法具有较好的去噪效果,能够在压制噪声的同时,最大限度地保留真实的有效信号。

