预制-现浇叠合拱板满跨堆载试验研究
杨 勇 周蓉峰 柳 献
1. 上海申通地铁集团有限公司 上海 201103;
2. 上海轨道交通十五号线发展有限公司 上海 200063;
3. 上海市机械施工集团有限公司 上海 200072;
4.同济大学土木工程学院 上海 200092
国内的无柱大跨度地铁车站目前多沿用传统的平板式顶板,通过采取一些加腋手段减小顶板跨中的弯矩,或者提高顶板跨中的承载能力。林作忠[1]和刘立[2]指出,广州地铁2号线琶洲—三元里段有近1/3的大跨度车站采用了无柱设计,这些车站仍沿用箱形框架结构,并选取顶板加密肋梁和变截面顶板这2种方案进行建设。潘冠全[3]对采用变截面顶板方案建设大跨度无柱车站的广州地铁11号线大金钟站的结构设计作了简要说明。近年来,广州地铁积累了不少相关建设经验,决定进一步改进施工和设计方法,预期在11号线建造顶板加腋的大跨无柱地铁车站,以提高承载能力[4-5]。乌鲁木齐轨道交通1号线的南湖广场站是国内地铁车站选用大跨无柱箱形框架结构的又一个案例[6]。
除了常见的箱形框架结构,国内大跨度地下车站还有一些其他较少采用的形式。张亚辉等[7]介绍了国内首个明挖拱形无柱结构地铁车站——青岛地铁3号线保儿站的设计。王福文[8]介绍了青岛地铁清江路站这一大跨度岛式暗挖车站,其断面为类似于公路隧道的无柱拱形形式。李凡[9]介绍了新京张城际铁路八达岭大跨度地下车站采取大跨度穹顶结构作为其顶棚的创新设计,由于跨度较大,该新型结构的设计与施工成为了一个较大的挑战。孙俊利[10]介绍了北京地铁6号线车公庄站的设计,该站是目前国内运用洞柱逆作法施作的最大跨度暗挖双层单拱无柱车站,在暗挖大拱节点设计方面有所创新。
作为大跨地铁车站,上海轨交15号线吴中路地铁车站顶板采用的是预制-现浇叠合拱板结构,是全国首个应用预制拱形顶板吊装工艺的地铁车站。为探究拱形顶板在正常运营工况下的结构性能,保证设计的可靠性和安全性,在距离较近的姚虹路地铁车站现场,开展了足尺的预制-现浇叠合拱板满跨堆载试验。本文简述了该足尺试验的概况,分析试验结构在满跨堆载时的受力性能,并得出一些在设计阶段可以参考的规律和建议。
1 试验方案
1.1 试验试件
本次试验的对象为一叠合拱结构,其轴线为圆弧形,半径为15.1 m、跨度为19.8 m、矢高为3.7 m。叠合拱的截面形式为矩形,高度为1 m、宽度为2.95 m,如图1所示。预制部分厚度为10 cm、肋梁高度为50 cm,2个预制拱壳在现场安装后形成一个三铰拱,然后以此三铰拱作为底模,在上面绑扎钢筋笼、现浇混凝土,形成预制-现浇叠合拱结构,混凝土硬化后三铰拱转变为无铰拱。
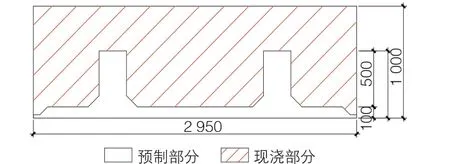
图1 叠合拱截面示意
1.2 试验装置
试验装置由叠合拱板、固定支座、滑动支座、拉索、堆载台阶和配重块等组成,结构如图2所示。
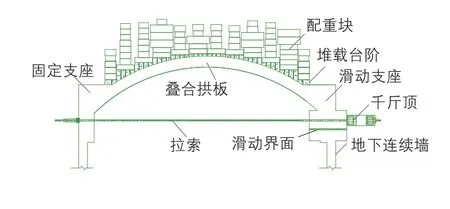
图2 试验装置结构示意
加载采用4种配重块,为3种不同规格的10 t配重块和1种2.8 t配重块。10 t配重块的尺寸分别为2 840 mm×1 000 mm×560 mm(1#)、2 500 mm×1 600 mm × 460 mm(2#)、2 112 mm×2 050 mm×680 mm(3#);2.8 t配重块的尺寸为900 mm×900 mm×500 mm。本次加载共使用10 t配重块(1#)29块、10 t配重块(2#)17块,10 t配重块(3#)8块、2.8 t配重块37块。配重块的加载方式为按顺序进行堆叠。加载时,分层均匀从两侧向中间对称叠放配重块,置于结构上事先浇筑的素混凝土台阶表面。
试验通过控制滑动支座端千斤顶的荷载调节拉索的张力,进而改变拱脚支座对拱的约束,从而模拟不同的土压力和地下连续墙刚度对于叠合拱壳和支座节点的影响。滑动支座的构造如图3所示。

图3 滑动支座的构造
1.3 试验过程
试验采用荷载-位移联合控制模式,荷载时程曲线如图4所示,位移时程曲线如图5所示。
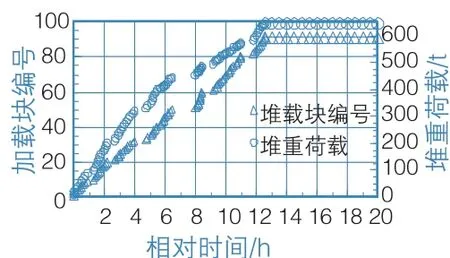
图4 荷载时程曲线
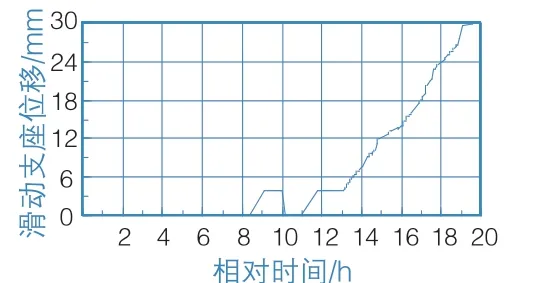
图5 位移时程曲线
整个过程可以分为几个步骤:
1)按设计的堆载顺序逐步堆载,直到堆载至设计荷载,即485 t。在此过程中,通过调整千斤顶荷载控制滑动支座位移在初始位置±1 mm范围内。
2)以0.3 mm/级的速度控制滑动支座向跨外滑动至3.7 mm。
3)滑动支座位移控制在3.7 mm,继续堆载至535 t。
4)通过调整千斤顶荷载使滑动支座位移回到初始位置。
5)滑动支座位移控制在初始位置,继续堆载至572 t。
6)以0.3 mm/级的速度控制滑动支座向跨外滑动至3.7 mm。
7)在竖向堆载572 t、支座位移3.7 mm的基础上,继续堆载和释放支座位移。滑动支座位移控制在3.7 mm附近,继续堆载至644 t,即设计荷载的1.33倍;分级控制滑动支座向跨外滑动至30 mm。受加载场地和设备装置的限制,试验终止。
1.4 测试方案
为研究整个结构在满跨堆载阶段的位移变形情况,选取了拱脚、拱顶、滑动界面等重要位置进行位移量测。在试验过程中测量了竖向位移、水平位移、预制拱拼装形成的接缝位置的错台和张开等数据,并根据所关注的内容安装了拉线位移计、一维位移传感器等,各测量仪器的总体布置如图6所示。在各处同类型的测量仪器均设2个,括号内的编号为从拱结构西侧所见的测量仪器编号。

图6 测量仪器的总体布置
在全跨选取了10个截面布设钢筋应变和混凝土应变的测点,测试截面的位置为跨中、拱脚和四等分点。从南侧拱脚开始,按顺时针方向依次给截面编号。其中,5、6号截面在跨中。在同一截面内,采用箔式应变片量测预制拱壳底面混凝土应变和钢筋应变,采用振弦式应变计量测现浇层钢筋的应力,测点布置如图7所示。试验中所用的全部应力应变测试仪器种类和数量如表1所示。
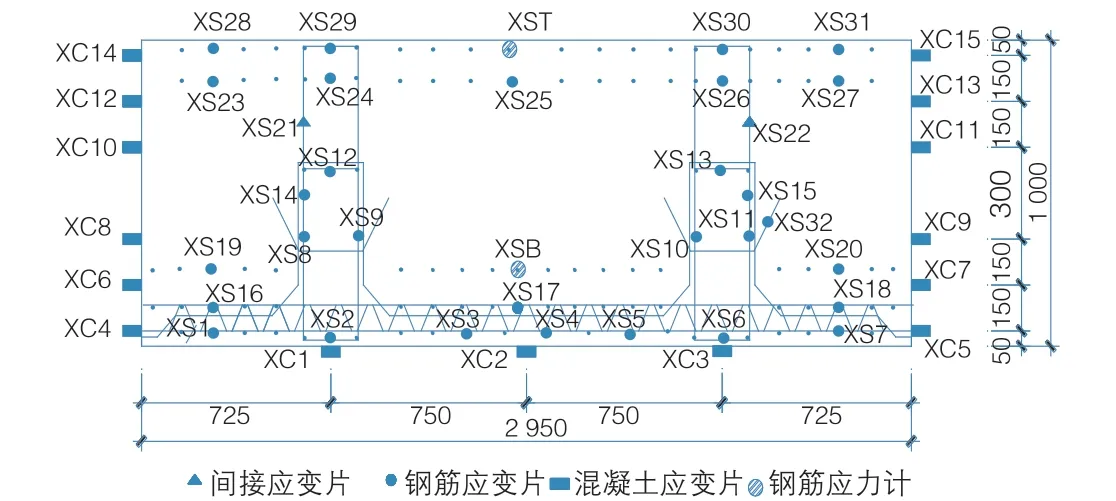
图7 截面内应力应变测点布置

表1 试验测试仪器数目统计
此外,为观察裂缝,提前在拱板东、西侧面和拱底面进行粉刷和网格线的绘制。东、西侧面网格大小为100 cm×20 cm,底面网格大小为100 cm×75 cm。在整个试验过程中,对裂缝分布情况、长度和宽度均及时进行了记录。
2 试验结果与分析
2.1 结构变形
在达到设计荷载485 t之前,拱顶处竖向位移基本保持不变。当堆载达到485 t时,拱顶处竖向位移的增量为-0.64 mm,在此过程中,拱顶有向下的位移趋势,但可以忽略不计,这证明该叠合拱板结构的刚度较大。其后,由于强制滑动支座发生向跨外或跨内的位移,导致拱顶产生明显的竖直向下或向上的位移,而在堆载时,拱顶竖向位移的变化值却是很微弱的。拱顶竖向位移在全过程中的变化情况如图8所示。

图8 拱顶竖向位移全过程曲线
当堆载达到644 t时,拱顶竖向位移值为-1.79 mm。在释放滑动支座位移到30 mm的过程中,拱顶竖向位移变化规律与支座位移规律基本一致,呈线性增长趋势。当保持堆载644 t,并使滑动支座达到30 mm时,拱顶竖向位移值达到-18.65 mm,但仍不足跨度的1/1 000。
在试验进行的前13 h,堆载和微调滑动支座等操作对拱顶竖向位移、两拱脚相对水平位移的影响较为明显,而对两拱脚的竖向位移影响较弱,如图9所示。

图9 拱脚竖向位移
13 h之后,在逐步释放滑动支座位移的过程中,叠合拱轴线变平缓,其曲率半径增加,导致各点竖直下移,根据几何关系,最大下移量产生在跨中附近。两拱脚的竖向位移也随支座位移的增加而增加,其最值相近且均小于-4 mm。各接缝处(拱顶、2个拱脚)的张开量如图10所示,错台量如图11所示。试验过程中,各接缝产生的张开或错台变化较小,错台的最终测量值均小于0.2 mm,张开的最终测量值均小于1 mm。意味着在混凝土硬化后,两半跨之间及侧墙与拱板之间能形成一个整体共同受力,因此,结构接缝处连接性能良好,侧墙对拱壳结构变形的约束较强。
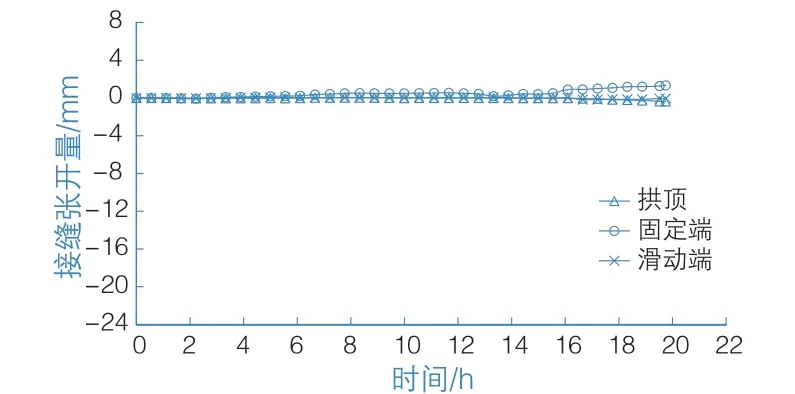
图10 接缝处的张开量
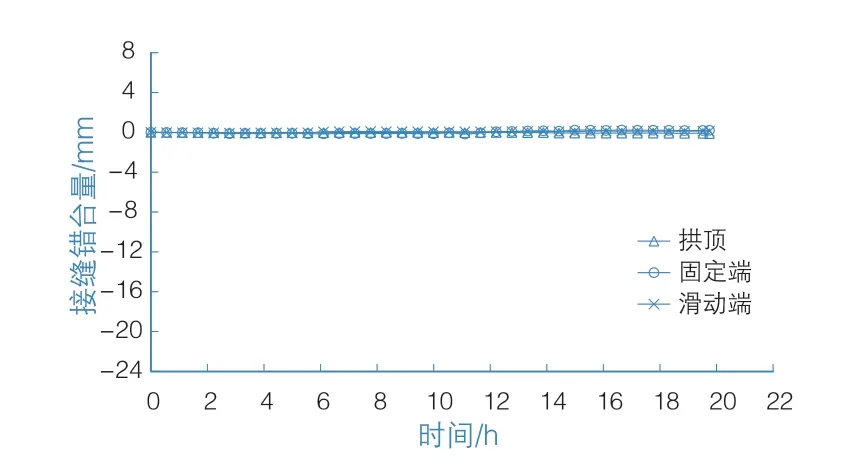
图11 接缝处的错台量
2.2 结构受力
2.2.1 裂缝现象
在拱结构上堆载485 t(设计荷载),并释放滑动支座位移达到3.7 mm之前,在混凝土结构表面观察无裂缝。直至竖向堆载达到644 t、支座位移等于24 mm时,叠合结构出现了受力裂缝,其宽度不足0.02 mm,长度达42 cm。这说明预制结构开始被破坏,但程度很轻微。当滑动支座位移释放到30 mm时,新出现的裂缝多为贯穿预制层的拉裂缝,裂缝宽度为0.02 mm,裂缝最大长度达到50 cm。试验最终状态下的裂缝分布如图12所示。

图12 裂缝分布示意
根据表观现象可知,裂缝容易集中出现在跨中附近,说明叠合拱结构的跨中部位受力较大,容易率先被破坏;预制拱部分较先开裂,且出现贯通裂缝,证明预制层能分担适当的内力,该叠合结构的两部分共同受力的效果良好。
2.2.2 预制层部分
在第1阶段,预制层靠近跨中的底排钢筋应变接近0,意味着最大正弯矩截面的混凝土全截面受压(弯矩以内侧受拉为正)。从跨中到拱脚,底层钢筋压应力有增大趋势,这是跨中受最大正弯矩、拱脚受最大负弯矩导致的。拱脚的预制层底排钢筋最大压应变为200 με,对应钢筋应力为-40 MPa(轴力以受拉为正),计算此处混凝土压应力约为6.5 MPa,其值远小于预制层混凝土(C35等级)的抗压强度。因此,与裂缝观察结果吻合,预制层混凝土不会压裂,拱脚接缝是受力安全的。
拱结构跨中附近预制层底排钢筋的应力在支座位移增加过程中正向增长,即有受拉趋势,拉应力增量在跨中处最大,向拱脚方向逐渐减小,最大增量为32 MPa,等效混凝土拉应力为4.8 MPa,大于C35混凝土抗拉强度,因而拱顶底部混凝土拉裂。拱脚处预制层底排钢筋应力呈负向增长,即逐渐受压,但压应力增量较小,最大为-15 MPa,不会导致混凝土压裂。
2.2.3 现浇层部分
在试验进行的前14 h内,结构加载以堆载为主,在此过程中,叠合拱结构的内力以轴力为主。尽管跨中受正弯矩,拱脚受负弯矩,各截面现浇层部分还是表现为受压状态,其压应力增量相近且较小,应力范围仅为-20~0 MPa。
当试验进行13 h后,试验加载主要表现为释放支座位移。在此过程中,拱脚处仍保持为全截面受压,且该处现浇层内钢筋的压应力增量较小,最大增量值出现在底部钢筋,约为5 MPa。而其余监测截面现浇层内钢筋有逐渐转变为顶部受压、底部受拉的趋势,并且此趋势在越接近跨中处表现得越明显。所有观测截面的现浇层内钢筋应力增量整体范围为-32~10 MPa,跨中受正弯矩,拱脚受负弯矩。
在释放支座位移前后,跨中现浇层钢筋内力的变化速率显然差别较大,在释放位移前的钢筋内力增加速率远小于释放位移之后。因此,跨中对支座位移的影响是十分敏感的。
跨中顶排钢筋呈受压趋势,其应力增量为10 MPa,而底排钢筋呈受拉趋势,其应力增量为30 MPa。但在全过程中,现浇层内钢筋应力总量是远远小于钢筋屈服应力的,因此,叠合拱板结构的受力状态是非常安全的。
2.2.4 叠合拱内力
分别采用了2种计算模型对结构受力进行了分析。2种模型仅存在截面刚度的差别,其余条件相同。其一为整体刚度模型,即认为两层完全为一整体,以完成状态的截面考虑其惯性矩和刚度。其二为叠加刚度模型,即分别考虑两层的截面形状,分开计算惯性矩和刚度后再叠加。
当试验进行到11.65 h时,试验以荷载控制为主,支座位移较小。此时,2种模型的结果很接近,而根据实测数据反算的内力,与理论计算的规律和数值均很相近。此时,拱结构全跨受压,在跨中附近受正弯矩,在拱脚附近受负弯矩,其具体内力值如表2所示。表格中的“偏差”是指整体模型、叠加模型结果偏离实测结果的差别程度。对于轴力而言,3条曲线在各处的吻合程度较好,其规律为拱脚处的轴压力最大,往跨中逐渐减小。实测数据反算轴力略大于理论计算结果,偏差程度在10%~25%之间。对于弯矩而言,三者均表现为拱脚处的负弯矩绝对值大于跨中处的正弯矩绝对值,而实测的弯矩差别程度明显大于理论计算的差别程度。在跨中位置3条曲线的差别较大,实测跨中弯矩小于理论计算,而在靠近拱脚区域实测的弯矩又偏大。这些现象说明理论计算模型低估了实际结构完成时,跨中区域的刚度相对拱脚和支座减小的程度,使弯矩分配程度有差别。

表2 试验进行到11.65 h时不同截面内力值对比
当试验进行到13.23 h时,试验以位移控制为主,竖向堆载保持不变。具体内力值如表3所示。

表3 试验进行到13.23 h时不同截面内力值对比
此时,拱结构依然全跨受压轴力,在跨中附近受正弯矩,在拱脚附近受负弯矩。采用2种模型计算得到的内力结果规律和数值很接近,根据实测数据反算的内力规律与模型结果规律十分相似,而实测轴力值大于理论模型计算的轴力值,偏差程度基本在22%~39%之间,实测弯矩值则小于理论模型计算的轴力值。在计算模型中,未考虑位移控制阶段结构变形较大而产生的附加内力带来的影响,而仍基于结构初始位置和形状计算,这可能是计算结果与实测结果有较大偏差的原因之一。
综上,2种模型计算得到的结构内力比较接近。以堆载控制为主的试验阶段,结构形状变化较小,计算结果与实测结果匹配程度较高,计算模型在此时的适用性较大。而在支座位移较大的位移控制阶段,相比试验反算内力,计算得到的轴力偏小,弯矩偏大,计算模型偏保守,但仍可用于设计。
3 结语
1)在堆载达到设计荷载485 t(8.42 h)时,拱顶、拱脚的竖向位移和各接缝处的错台、张开的量值可忽略不计,这表明结构已经转化成无铰拱,两层结构能够较好地作为一个整体协同受力。
2)当释放滑动支座位移达到30 mm时,拱顶竖向位移仅约为跨度的1/1 000(20 mm),说明该叠合拱板结构的刚度是完全充足的。
3)叠合拱板结构在以荷载主导的满跨堆载阶段,全截面受压,拱效应明显。后期随着支座位移的释放,跨中截面底部钢筋出现拉应力,拱效应逐步减弱。钢筋的最大拉应力和压应力均出现在跨中位置,分别约为8.8 MPa和-53 MPa,皆远小于钢筋的屈服应力,说明拱板结构的安全储备较大,结构存在优化设计的空间。
4)叠合拱板结构的跨中底部最先开始开裂,随后逐渐发展为贯通裂缝,证明预制层能分担适当的内力,该叠合结构两部分共同受力的效果良好。
5)相对堆载而言,叠合拱板结构对支座位移的响应更加强烈,因此支座侧向位移是控制该叠合拱板结构安全的重要指标。
6)采用整体刚度模型和叠加刚度模型计算得到的内力相近,均可用于设计计算。

