AI-Based Optimization of Handover Strategy in NonTerrestrial Networks
ZHANG Chenchen, ZHANG Nan, CAO Wei, TIAN Kaibo, YANG Zhen


DOI: 10.12142/ZTECOM.202104011
http://kns.cnki.net/kcms/detail/34.1294. TN.20211028.1117.002.html, published online October 28, 2021
Manuscript received: 2021-04-16
Abstract: Complicated radio resource management, e.g., handover condition, will trouble the user in non-terrestrial networks due to the impact of high mobility and hierarchical layouts which co-exist with terrestrial networks or various platforms at different altitudes. It is necessary to optimize the handover strategy to reduce the signaling overhead and im ? prove the service continuity. In this paper, a new handover strategy is proposed based on the convolutional neural network. Firstly, the handover process is modeled as a directed graph. Suppose a user knows its future signal strength, then he/she can search for the best handover strategy based on the graph. Secondly, a convolutional neural network is used to extract the underlying regularity of the best handover strategies of different users , based on which any user can make near-optimal handover decisions according to its historical signal strength. Numerical simulation shows that the proposed handover strategy can effi ? ciently reduce the handover number while ensuring the signal strength.
Keywords: convolutional neural network; directed graph; handover; low earth orbit; non- terrestrial network
Citation (IEEE Format): C. C. Zhang, N. Zhang, W. Cao, et al., “AI-based optimization of handover strategy in non-terrestrial networks, ”ZTE Communications, vol. 19, no. 4, pp. 98 – 104, Dec. 2021. doi: 10. 12142/ZTECOM.202104011.
1 Introduction
The non-terrestrial network (NTN) has been regarded as asupplementtothe5Gterrestrialmobilenetwork sinceitprovidglobalcoverageandservicecontinu ? ity[ 1]. Compared with terrestrial networks, the hando? ver in NTN is more frequent and complex.In this paper, a handoveroptimizationmethodisproposedandappliedtoa typical NTN scenario, i. e. , a low earth orbit (LEO) satellite network.A LEO is an orbit around the earth with an altitude between 500 km and 2 000 km[ 1]. Compared with geostation? ary earth orbit satellites, the LEO satellites have much lower path-loss and propagation delay.Therefore, the third genera? tion partnership project (3GPP) NTN study item has regarded the LEO satellites as the key to providing global broadband In ? ternet access.Suppose the orbit is circular, the satellite will move around the earth at a constant velocity which is inverse ? lyproportionaltothesquarerootof theorbitaltitude. Because of the low altitude, the LEO satellites have a high speed with respect to the earth, and terrestrial user equipment (UE) needs to frequently switch to new beams to keep connectivity. In order to ensure the quality of the Internet service, the opti? mization for NTN handover strategy needs to be carefully in ? vestigated.
Previous studies generally make handover decisions based on one or more predefined criteria. The most commonly used criteria include the elevation angle[2] , remaining service time[3] and the number of free channels[4] , whichcorrespond to the signal strength, handover number and satellite burden, respec ? tively. But these methods cannot get an overall optimization. InRef.[5],anoveralloptimizationmethodisproposedby modeling the handover process by a directed graph. Each sat? ellite is denoted by a node, then the best handover strategy is obtained by searching the shortest path. However, in Ref. [5] each satellite node is invariable during the handover process.UE needs to perform handover as soon as entering the cover? age of another beam and cannot choose an appropriate time. Besides, the UE needs to predict its coverage condition in a fu ? ture time to construct the graph, which may bring unexpected error and is beyond the capability of standard 5G UE.
Inrecentyears,someartificialintelligence(AI)tech? niques have been applied to search for overall optimization onhandover.ThemostoftenusedtechniqueisQ-learn? ing[6 –8] ,whichistypicalmodel-freereinforcementlearning (RL). In Q-learning, some properties of UE are defined as its state, and the handover operation is defined as its action. Nu ? merical simulation is used to iteratively train the Q-table (the reward of each action for each state) until its convergence. Then the UE can decide whether to perform handover accord ? ing to its state. Furthermore, the Q-table can be replaced by a neural network for an infinite number of states. In Ref. [8], the handover in a LEO scenario is optimized by Q-learning. The state of UE is composed by its position, accessible satel? lites and whether handover is processed in this time slot. In each time slot, the UE is required to know its state and will choose a satellite for handover, which is a really strong re ? quirement for ordinary UE. Besides RL, a recursive neural network (RNN) can also be used for handover optimization. Refs.[9] and[ 10] apply RNN for handover optimization in terrestrial millimeter wave mobile systems and vehicular net? works, respectively. However, in a LEO scenario, the beamswitch is fast, and the signal series of one beam may be too short for the RNN to make decisions.
In practical terms, a handover strategy with a low require ? ment for UE capability is desired to reduce the handover num ? ber while ensuring the reference signal received power (RSRP). In this paper, a convolutional neural network (CNN) based han? dover strategy optimization is proposed. Firstly, an amount of UE is randomly generated within the coverage of a satellite. The RSRP series of UE is generated based on the channel model in Ref. [ 1] and the simulation assumption in Ref. [ 11]. Secondly, the graph-based method in Ref. [5] is improved by setting each satellite in different time slots as different nodes. The improved methodis used to find the best handoverstrategies for each piece of UE. Thirdly, the internal relation between the histori ? cal RSRP series and the best handover decision is extracted by a customized CNN. Since standard 5G UE needs to periodically measure the RSRP of the serving cell and adjacent cells, the UE can perform a sub-optimal handover strategy based on the historical measurements. The main contributions of this paper are summarized as follows.
· This paper proposes a novel directed graph model for the handover process. In this model, each beam in different time slots is viewed as different nodes, and the weight of an edge is determined by the RSRP and the beam identities of the two correspondingnodes.Supposethebeamcoverageandthe RSRP of UEare predictable, the best handover strategy for the UE can be found based on the model.
· A CNN is constructed based on the classical LeNet-5[ 12] for handover optimization. The results of thedirectedgraph model are used to train the parameters of the CNN. Using thetrained CNN, any UE in the LEO network can perform subop ? timal handover based on its historical RSRP.
The rest of this paper is organized as follows. Section 2 de? scribes the LEO network model and the motivation of hando ? ver optimization. In Section3, a novel directed graph-based model is proposed for the handover process. A CNN structure is constructed and the results of the directed graph model are used to train the CNN. The effectiveness of the CNN is numer? ically evaluated in Section 4. Finally, Section 5 concludes this paper.
2 Background
2.1 System Model
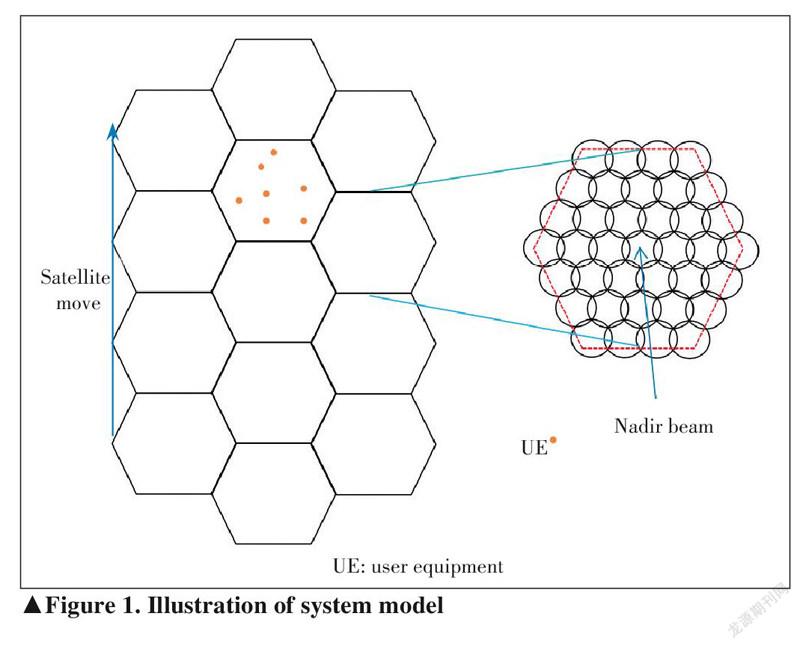
A typical LEO satellite network consists of several circular orbits,andeachorbitcontainsseveralevenlyspacedsatel ? lites. This paper considers the scenario in Fig.1 where each hexagon denotes the coverage of a satellite. Referred to the as ? sumptions[ 11 – 13]used in 3GPP NTN study item, each satellite is assumed to have 37 beams that form the hexagon coverage. The UE is assumed to locate within a hexagon in the initial time, and the satellites in the three adjacent orbits are consid ? ered to evaluate the RSRPs on the UE. During the flight of thesatellites,apieceof UEneedstoperiodicallymeasurethe RSRPs of different beams and make handover decisions.
ThebeamlayoutinFig.1decidesthecenterof the37 beams[ 13]. Suppose the satellite is above a plane, then the di? ameter of the nadir beam on the plane can be computed based on the 3 dB angle. It is easy to compute the other 36 beam cen? ters on the plane according to Fig. 1. Then the bore-sight di? rections of the 37 beams can be determined. The angles be? tween co-orbital satellites and adjacent orbits are also calculated to fulfill the coverage shown in Fig. 1.
2.2 Motivation
In 3GPP simulation assumption Set- 1[ 11] , a satellite with an altitude of 600 km has a beam diameter of 50 km and a veloci? ty of 7.56 km/s. Therefore, a piece of UE can only connect to one beam in 6.6 s at most. Because of the noise and the over? lapping of different beams, the handover will happen more of? ten. In addition, because of the long propagation time, each handoverprocedureneedsalongertimeandwillconsume more time-frequency resources. Therefore in a LEO network, the handover has a time lag and causes a large signaling over? head. To reduce the overhead and improve service continuity, the handover strategy needs to be optimized for the following targets.
· Predict the handover decision to compensate the time lag.
· Reduce the handover caused by noises, including shadow fading, multipath fading, and white Gaussian noise.
· Identify and suppress the handover in this situation. As shown in Fig. 2, a piece of UE near the beam edge may have a short serving time for some beams.
In this paper, an overall handover optimization is obtained in the directed graph model for each piece of UE. The com? mon features of the optimized strategies for different UE are extracted usingCNN to fulfill the targets withoutstrong re ? quirements for UE capability.
3 Handover Strategy Optimization Based on CNN
In a LEO satellite network, the satellites fly along predeter? mined circular orbits, so the change of the RSRP has strong regularity. The regularity can be used to improve the handover decision. Specifically, in each time slot, the previous N RSRP values of UE form a series, and some kinds of RSRP series im ? ply that the UE should start handover. In this section, those kinds of RSRP series are found in two steps. First, the RSRPof each UE during a long period is measured and recorded. A directed graph model is proposed to search for the best hando ? ver decision in every time slot. Then the handover decision is regarded as the label for the previous N RSRP values of that time slot to be trained by the CNN. The proposed CNN can ef? ficiently extract the common regularity of handover decisions for different UE.
3.1 A Novel Directed Graph Based Model
The directed graph based model in Ref. [5] is designed to search the optimal handover strategy. However, the UE needs to start handover as soon as entering the coverage of the next satellite,whichmeansitcannotchooseamoreappropriate handovertime.Thissectionproposesanimproveddirected graph based model to solve the problem.
3. 1. 1 Referenced Model in Ref. [5]
In Ref. [5], every satellite is modeled as a node. If the begin? ning or end of the coverage of one satellite is between another satellites coverage period, then there exists a directed edge be ? tween the two satellites, which means that a piece of UE can perform a handover between the two satellites. The weight of the edge is determined by the chosen criteria in the two satel ? lites. For example, suppose only the criterion “handover num? ber”is considered, then the weight of every edge should be set to 1. If other criteria such as “number of free channel”and“el? evationangle”are considered, the weight can be set according to the two criteria of the target satellite. The Dijkstras shortest path algorithm can be used to search the path with the smallest or largest weight. By choosing appropriate criteria, the resulting path becomes the overall optimal handover strategy.
An example of satellite coverage time and the corresponding directedgraphin the referencedmodelareshowninFig.3. Node 0 denotes the initial time and other nodes denote four sat? ellites. In this model, the node and the edge weight are invari ? able during the handover process. The weights of the edges cannot reflect thechange process of theelevationangles or other criteria of the satellites. The UE can only assume that the handover happens as soon as it enters the coverage of an ? other satellite.
3. 1.2 Proposed Model
By considering the variation of satellites during the hando ? verprocess,anovelmodelcanbeconstructedtogeneratemore reasonable optimization for handover. The basic idea is to regard a beam in different time slots as different nodes. As shown in Fig. 4, we assume that in each time slot the serving beam of UE is one of the K strongest beams. The beamTK de? notes the K-th strongest beam in the T-th time slot. Every two nodes in adjacent time slots are connected by an edge, which means that the handover between them is possible.
Similar to Ref. [5], the weights of the edges can be set ac ? cording todifferentcriteria for overalloptimization. For the sakeofsimplicity,thispaperonlyconsiderstheRSRP strength and handover number. Then the weight of the edge from beamT1K1 to beamT2K2 can be defined as
where RSRPT1K1 denote the RSRP value of beamT1K1, and han? doverFlag = 1 if beamT1K1 and beamT2K2 are two different beams. When the signal-to-noise ratio is small, the channel capacity is proportional to the signal strength.
Therefore w1 ×RSRPT1K1 in Eq. ( 1) denotes the benefit of con? nectingbeamT1K1 inT1-thtimeslot,wherew1 isapredeter? mined parameter. Similarly, the parameter w2 is chosen accord? ing to the degree of the negative impact of one handover. By using the Dijkstras shortest path algorithm, we can find the longest path from the first time slot to the last time slot, which is actually the optimal handover strategy for this UE.
3.2 CNN Based Optimization for Handover
RSRP is defined as the linear average over the power of the resourceelements thatcarrysome predefined referencesig? nals. Assume UE can predict the RSRP of different beams for a long period, then the method in Section 3. 1.2 can be used to find the optimal handover strategy.However, in most cases, UE only knows its historical RSRP. Standard 5G UE needs to measure theRSRPs of detectable cells and handover to thestrongest cell if its RSRP minus a predetermined threshold is larger than the serving RSRP. In this way, the information hidden in the historical RSRP is ignored. Actually, at least in the LEO scenario, the historical RSRP can help UE to make sub ? optimal handover decisions. The series of historical RSRPs of the strongest K beams in each time slot forms a two-dimension? al matrix. A customized CNN is used to optimize the handover decision based on the matrix in this section.
CNN is an effective tool to elicit information from two-di? mensionaldata.Ithasbeen widelyusedtoextract features from images. A classical CNN consists of one or more convolu ? tional layers, pooling layers, and fully-connected layers. The features of the input data are extracted layer by layer, and are summarized in the last fully-connected layer to generate the fi ? nal output. Compared with the fully-connected layer, the con? volutional layer takes advantage of the strong local spatial cor? relation in natural images and only has a few parameters to be trained. It is worth mentioning that the matrix of RSRP also has the “local spatial correlation”, i. e., the cooperation of the RSRP values in adjacent time slots and the RSRP values of the nearest 3 or 4 beams are more likely to contain informa? tion for handover decisions. Therefore it is suitable to apply CNN to the problem of handover.
Intuitively, the RSRP series in the LEO network has strong regularity,soarelativelysimpleneuralnetworkstructure should be chosen to reduce the training time and prevent over? fitting. The LeNet-5[ 12]is firstly designed for character recogni ? tion and is a relatively simple modern CNN structure. The de? fault input of LeNet-5 is a matrix of the size of 32×32. Howev ? er, in the LEO network model presented in Section2. 1, the number of detectable beams for one piece of UE is generally smaller than 32. Therefore the size of the input data needs to be reduced. Actually, in the simulation, the number of consid? ered beams in each time slot is set to be10. The length of a time slot is set to be 0.5 s and the RSRP values in the previous 10-time slots are used to form the input. Then the input of the CNN is a matrix of the size of 10× 10. In LeNet-5, two convolu? tional layers are used. The two convolution kernels both have the size of 5×5. Besides, two pooling layers are used to reduce the number of trained parameters. Because of the reduced in? put size, some layers in LeNet-5 need to be customized. First, one convolution kernel is reduced to the size of 3×3. Then the pooling layers are deleted since the number of parameters is not large. The structure of the resulting CNN is presented in Fig. 5. The output of size10 corresponds to the10 kinds ofhandoverdecisions,i. e.,oneofthe10 strongestbeamsis which the UE will connect in the next time slot.
The data preprocessing and the training procedure consist of four steps as follows.
1) For every piece of UE, generate the RSRP values of differ? ent satellites in every time slot. If one satellite is invisible or its signal is too weak to detect, the RSRP values are regarded as 0.
2) Compute the best handover strategy for every UE based on the proposed directed graph-based method in Section 3. 1.2.
3) For every UE in every time slot, the previous10 RSRPvalues of the 10 strongest beams are used to form 10× 10 input data. Thebesthandoverdecisiongeneratedintheprevious step is regarded as the corresponding label.
4) The input data and the corresponding labels from differ? ent UE are used to train the CNN in Fig. 5. After some ep? ochs, the testing accuracy will converge.
The trained CNN can be used to make suboptimal handover decisions for new UE. In each time slot, the UE extracts the historical RSRP values of the 10 strongest beams as the input of the trained CNN. The output contains 10 values and the in? dex of the largest value is regarded as the serving beam in the next time slot. It is worth noting that the handover decision is actually a prediction for the next time slot, so the time lag in the handover procedure can be compensated.
4 Simulation
Theproposedmethodsarenumericallyevaluatedinthis section. The simulation parameters are mainly referred to as the parameter Set- 1 in Ref. [ 11]. Some important parametersare shown in Table 1.
As described in Section 2. 1, the LEO network in simulation consistsof threeorbits.Eachsatellitehas37beamswhich form a hexagon. Some points are randomly generated within one hexagon in the UV plane. The projection of the points on the earth is calculated as the positions of the UE.
4.1 OptimalHandoverStrategyBasedonDirected Graph Model
WiththeconstructedLEOnetwork,theRSRPvalues for each UE are calculated in each time slot. The length of a onetime slot is set to be 0.5 s, and about 140- time slots are considered in the whole simu ? lation. The optimal handover strategy for each UE is generated by using the directed graph-based model in Section 3. 1.2.
In the graph-based model, the two param? eters w1 and w2 form a trade-off between RSRP strength and handover number and need to be predetermined. In this section,w is fixed and different w is evaluated toshow the change of handover number and average RSRP strength. Because of thelargepathloss, thereceivedpower of the strongest beam in one resource element is near 10? 17 W. There? fore, the w1 in Eq. ( 1) is set to be1017 , which means that the benefitof accessingthestrongestbeaminone-timeslotis around 1. Meanwhile, the value of w2 is set to be 0, 0.5, 1, 2, and 5. When w2=0, the UE will always connect to the stron ? gest beam. As shown in Figs. 6 and 7, with the increase of w2 ,the handover number and average RSRP will both decrease.
4.2 Performance of CNN in Handover Optimization
Three methods for handover optimization are compared in this section. The first method assumes the UE can predict its RSRPandmakehandoverdecisionsbasedonthedirected graph model. The second method means that the UE uses the trained CNN to make handover decisions. The CNN is trained by the results of the directed graph model with w2=1. In the third method, the UE is always served by the strongest beam.
Compared with the “strongest beam”method, the CNN can largely reduce the number of handovers without a requirement for UE capability. Figs. 8 and 9 show that the handover num ? ber of more than 70% of the UE is reduced by more than 1/4, while the average RSRP is only reduced by 3%.
5 Conclusions
ThispaperproposesaCNN-basedhandoveroptimization method for the LEO satellite network. The CNN structure is customized based on LeNet-5 and is used to extract the hid? den information in the historical RSRP. In order to produce the training data for CNN, a novel directed graph-based model is proposed to find the optimal handover strategy when the UE knows its futureRSRP. After the training, theCNNcan be used to find a suboptimal handover decision based on its his ? torical RSRP. In the simulation, the CNN is verified to be ef? fective in handover optimization. The number of handovers is significantly reduced while the average RSRP is only reduced by 3%.
The optimization of handover in satellite communication is relatively simple because of the strong regulation of the move ? ment of satellites. But the deep learning-based method can al? so be used in more complex scenarios. In order to extract the hidden regulation, a more advanced neural network structure may be needed, such as the attention-based neural network. The deep Q-learning is also worth investigating for a dynami ? cally changing environment.
References
[ 1] 3GPP. Study on new radio (NR) to support non terrestrial networks: 3GPP TR 38.811 [S]. 2018
[2] GKIZELI M, TAFAZOLLI R, EVANS B. Modeling handover in mobile satellite diversity based systems [C]//The 54th Vehicular Technology Conference. Atlan? tic City, USA: IEEE, 2001: 131 – 135. DOI: 10. 1109/VTC.2001.956570
[3] DEL RE E, FANTACCI R, GIAMBENE G. Handover queuing strategies with dynamic and fixed channel allocation techniques in low Earth orbit mobile satel ? lite systems [J]. IEEE transactions on communications, 1999, 47( 1): 89 – 102. DOI: 10. 1109/26.747816
[4] DEL RE E, FANTACCI R, GIAMBENE G. Efficient dynamic channel alloca? tion techniques with handover queuing for mobile satellite networks[J]. IEEE journalonselectedareasincommunications,1995,13(2):397– 405.DOI: 10. 1109/49.345884
[5] WU Z F, JIN F L, LUO J X, et al. A graph-based satellite handover framework forLEOsatellitecommunicationnetworks[J].IEEEcommunicationsletters, 2016, 20(8): 1547 – 1550. DOI: 10. 1109/LCOMM.2016.2569099
[6] YAJNANARAYANA V, RYD?N H, H?VIZI L. 5G handover using reinforce? ment learning [C]//IEEE 3rd 5G World Forum (5GWF). Bangalore, India: IEEE. 2020: 349 –354. DOI: 10. 1109/5GWF49715.2020.9221072
[7] CHEN Y, LIN X Q, KHAN T, et al. Efficient drone mobility support using rein ? forcement learning [C]//IEEE Wireless Communications and Networking Confer? ence(WCNC).Seoul,SouthKorea:IEEE,2020:1– 6.DOI:10. 1109/WCNC45663.2020.9120595
[8] CHEN M T, ZHANG Y, TENG Y L, et al. Reinforcement learning based sig? nal quality aware handover scheme for LEO satellite communication networks [M]//HumanCenteredComputing. Cham:SpringerInternationalPublishing, 2019: 44 –55. DOI: 10. 1007/978-3-030-37429-7_5
[9] ALKHATEEB A, BELTAGY I, ALEX S. Machine learning for reliable mmwave systems: Blockage prediction and proactive handoff [C]//IEEEGlobalConfer? ence on Signal and Information Processing (GlobalSIP). Anaheim, USA: IEEE, 2018: 1055 – 1059. DOI: 10. 1109/GlobalSIP.2018.8646438
[ 10] ALJERI N, BOUKERCHE A. An efficient handover trigger scheme for vehicu ? lar networks using recurrent neural networks [C]//The 15th ACM InternationalSymposium on QoS and Security for Wireless and Mobile Networks. New York, USA: ACM. 2019: 85–91. DOI: 10.1145/3345837.3355963
[11] 3GPP. Solutions for NR to support non-terrestrial networks (NTN): 3GPP TR 38.821 [S]. 2019
[12] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition [J]. Proceedings of the IEEE, 1998, 86(11): 2278 – 2324. DOI: 10.1109/5.726791
[13] 3GPP. On beam layout definition for NTN system level simulations [EB/ OL]. [2021-04-16]. https://www.3gpp.org/DynaReport/TDocExMtg--R1-97-- 32823.htm
Biographies
ZHANG Chenchen (zhang.cc@zte.com.cn) received his B.S. degree in mathe?matics from Nankai University, China in 2013, and the Ph.D. degree in computer science and technology from Shanghai Jiao Tong University, China in 2018. He has been with ZTE Corporation since 2018. He is now a senior pre-research engi?neer in non-terrestrial network. His main research interests include satellite com?munications, random access, mobility management, neural network and NOMA.
ZHANG Nan received his bachelors degree in communication engineeringand masters degree in integrated circuit engineering from Tongji University , China in July 2012 and March 2015, respectively. He is now a senior engineer at the Department of Algorithms, ZTE Corporation and works on the standard ? ization of LTE and NR system. His current research interests are in the field of 5G channel modeling, MIMO, NOMA techniques, satellite/ATG communication and network architecture.
CAO Wei is a senior pre-research expert in ZTE Corporation. She received her Ph. D. degree in wireless communication from National University of Singapore in 2008. Her current research interests include non-terrestrial communication network and reconfigurable intelligent surface.
TIAN Kaibo received his masters degree from Xian Jiaotong University, Chi? na in 2008. Now he is the senior pre-research expert of ZTE Corporation and re ? sponsible for the pre-research of the Air-Space-Ground integrated network tech ? nology.
YANG Zhen received his B.S. degree in communication and information sys ? tem from University of Electronic Science and Technology of China in 2012. Since2012hehasbeen with ZTECorporation. Heisnowasenior pre-re? search engineer in wireless communications. His main research interests in? clude satellite communications, random access, mobility management, neuralnetwork and DPD.
- ZTE Communications的其它文章
- OTFS Enabled NOMA for MMTC Systems over LEO Satellite
- A Survey on Low Complexity Detectors for OTFS Systems
- Coded Orthogonal Time Frequency Space Modulation
- Truly Grant-Free Technologies and Protocols for 6G
- Performance of LDPC Coded OTFS Systems over High Mobility Channels
- Editorial: Special Topic on

