A Survey on Low Complexity Detectors for OTFS Systems

ZHANG Zhengquan, LIU Heng, WANG Qianli, FAN Pingzhi

Abstract： The newly emerging orthogonal time frequency space （OTFS） modulation can ob?tain delay-Doppler diversity gain to significantly improve the system performance in highmobility wireless communication scenarios such as vehicle-to-everything （V2X）， high-speedrailway and unmanned aerial vehicles （UAV）， by employing inverse symplectic finite Fouri ?er transform （ISFFT） and symplectic finite Fourier transform （SFFT）. However， OTFS modu?lation will dramatically increase system complexity， especially at the receiver side. Thus， de?signing low complexity OTFS receiver is a key issue for OTFS modulation to be adopted bynew-generation wireless communication systems. In this paper， we review low complexityOTFS detectors and provide some insights on future researches. We firstly present the OTFSsystem model and basic principles， followed by an overview of OTFS detector structures，classifications and comparative discussion. We also survey the principles of OTFS detectionalgorithms. Furthermore， we discuss the design of hybrid OTFS and orthogonal frequency di ?vision multiplexing （OFDM） detectors in single user and multi-user multi-waveform commu?nication systems. Finally， we address the main challenges in designing low complexity OT ?FS detectors and identify some future research directions.

Keywords： high mobility wireless communications; OTFS; ISFFT;SFFT; delay-Doppler diversity; iterative maximum ratio combining （MRC） detection; message passing detection

Citation （IEEE Format）： Z. Q. Zhang， H. Liu， Q. L. Wang， et al.，“A survey on low complexity detectors for OTFS systems， ”ZTE Commu ? nications， vol. 19， no. 4， pp. 03 – 15， Dec. 2021. doi： 10. 12142/ZTECOM.202104002.

1Introduction

Thenew-generationmobilecommunicationsystems[ 1] are the key enabler for the digital society in the next ten years and are expected to satisfy the requirements for high mobility applications such as vehicle-to-every? thing（V2X）services[2 –3] ， high-speed railwayservices[4 –5]，aswellas unmannedaerial vehicles（UAV）， which require the support of high mobility up to 500 – 1 000 km/h with accept? able quality of service （QoS）[ 1， 6].

However，highmobilitywirelesscommunicationssuffer from high Doppler spread， and the transmitted signals experi ? ence time-frequency doubly selective channel[7]. High Doppler spreadwillresultinveryseriousinter-carrierinterference （ICI）， especially in orthogonal frequency division multiplexing （OFDM） systems. Another challenge is to perform channel esti ? mation to obtain exact channel state information （CSI） of fast time-variant channels， even to the extent that the reported CSI is outdated. These challenges will seriously reduce the perfor? mance of conventional OFDM systems. To tackle the challenges of high mobility， learning-based channel estimation， flexi? ble subcarrier spacing and length of cyclic prefix （CP）， double demodulationreferencesignals（DMRS），i. e.，front-loaded DMRSandadditionalDMRS withconfigurable time-domain density， have been studied. However， these methods still treat high mobility as a negative factor， which results in very limit? ed performance improvements of OFDM systems.

Recently， the orthogonal time frequency space （OTFS） mod? ulationtechnology[8 –9]hasbeenproposedforhighmobility wirelesscommunications，andattractedincreasingattention duetoitsexcellentperformance.Thisnewtwo-dimensional （2D） modulation transforms high mobility into a positive factor by introducing inverse symplectic finite Fourier transform （IS? FFT）-based pre-processing before OFDM modulation and sym ? plectic finite Fourier transform （SFFT） -based post-processing after OFDM demodulation. With ISFFT/SFFT transforms， de? lay-Doppler （DD） domain is introduced in OTFS systems and the modulated symbols are transmitted in DD domain rather than time-frequency （TF） domain. The equivalent DD channel exhibits excellent features of separability， stability， compact? ness， and possible sparsity[9] ， which enables OFTS systems to obtain delay-Doppler diversity gain. Additionally， these excel? lent features are also beneficial for performing channel estima? tion under high mobility environments. OTFS modulation has also been submitted to 3GPP as a candidate waveform for 5G systems[ 10 – 12] ，andisregardedasapromisingwaveformfor next-generation wireless communications[ 13].

However，sinceeachmodulatedsymbolisspreadtothe whole TF resource grid by ISFFT operation in OTFS systems， thenumberof equivalentDDchanneldimensionsislarger than that of OFDM systems， which dramatically increases the complexityofsignaldetection.Toaddressthischallenge， some efforts have been devoted to the research of low complex ? ity OTFS detector structures such as decision feedback equal ? izer （DFE）[ 14] ， iterative maximum ratio combining （MRC） detec ? tor[15 – 16] ， non-iterative joint TF- and DD-domain detector[ 17] ， it? erative jointtime-andDD-domaindetector[ 18] ，non-iterative MRCdetectorwithcompensation[ 19] ，learning-baseddetec ? tor[20 –23] ， and separate low complexity OTFS detector[24]. Sever? alOTFSdetectionalgorithms，includinglinearminimum mean square error （MMSE） and zero-forcing （ZF） [25 –29]， mes? sage passing （MP）[30 –35]and its variants like approximate mes ? sage passing（AMP） [34 –36]，MRC[15 – 16] ， jointMP andMRC[37] ， hybrid maximum a posteriori （MAP） and parallel interference cancellation（PIC） [38] ， expectation propagation（EP） [39]， varia? tional Bayes （VB） [40] ， and iterative least squares minimum re ? sidual （LSMR）[41] ， have been studied.

Inthispaper，acomprehensivesurveyonOTFSdetector structures and detection algorithms is provided. We compare theadvantagesanddisadvantagesofeachOTFSdetector structure and detection algorithm， which can provide some in? sights for future research. We also provide classifications for OTFSdetectorsfromdifferentdimensions.Furthermore，westudy a hybrid OFDM-OTFS multi-waveform detection frame ? work. Finally， we discuss some challenges for low complexity OTFS detectors， and identify some future research directions. The rest of the paper is organized as follows. A brief discus ? sion on the OTFS system model and the principles of OTFS modulation are given in Section 2. In Section 3， a survey on thestate-of-the-artOTFSdetectorstructuresisprovided， while the research progress on OTFS detection algorithms is given in Section 4. In Section 5， a hybrid OTFS-OFDM multi- waveform detection framework is discussed briefly， while Sec ? tion 6 discusses the research challenges and identifies some future research directions， followed with conclusions.

2 Basic Principles of OTFS Modulation

The OTFS system model is shown in Fig. 1， which includes OTFStransmitterandreceiverstructures.Comparedwith OFDMsystems，OTFSsystemsaddISFFT-basedtransform precodingbeforeOFDMmodulationatthetransmitterside， whileSFFT-basedpost-processingisemployedafterOFDM demodulation at the receiver side. From the perspective of sys ? tem structures， OTFS systems can be regarded as a type of pre ? codedOFDMsystemsandcanbeeasilycompatiblewith OFDM systems. With the introduction of ISFFT/SFFT trans ? form， a new domain， i. e.， DD domain， is introduced. As a re ? sult， there are three domains in OTFS systems： DD domain，TF domain and time domain， while OFDM systems only have TF and time domains.

Considering an OTFS system with an N × MDD resource grid， at the OTFS transmitter side， the modulated symbols and pilots are mapped to the DD resource elements. The signal car? riedbythe（k，l） -thDDresourceelementisdenotedby xDD [ k， l ]fork = 0， 1，...， N - 1， l = 0， 1，...， M - 1.Then，the symbols xDD [ k， l ] in the DD domain are converted to the sym ? bolsxTF [ n， m ]intheTFdomainusingtheISFFTasxTF [ n， m ] = ISFFT （ xDD [ k， l ]） =xDD [ k， l ] ej2πN（nk）- M（ml）forn = 0， 1，...， N - 1， m = 0， 1，...， M - 1.Next，thesignals xTF [ n， m ] in the TF domain is converted to the symbols in the dimedomainsignalasx （ t） = IFFT（ xTF [ n， m ]） =xTF [ n， m ] gtx （ t - nT ） ej2πmΔft - nTandistrans?mitted through the channel. At the OTFS receiver side， the re?ceivedsignalinthetimedomainis y （ t） = ∫∫ h （τ ，υ ） x （ t -τ ） ej2πυ （ t - τ ） dτdυ. After OFDM demodulation（i. e.， FFT trans ? form），thesymbolsintheTFdomainaredenotedby yTF [ n， m ]. Then， applying SFFT on yTF [ n， m ]， the symbols in the DD domain can be obtained asyDD [ k， l ] =SFFT （ （yTF [ n， m ]） =yTF [ n， m ] e-j2π N（nk）- M（ml）.Finally，thetransmitted symbols xDD [ k， l ] can be recovered from yDD [ k， l ] through the OTFS detector.

As shown in the expression for ISFFT， a DD symbol carried by a DD resource element is spread to alltheTFresourceelements， whichenablesOTFSsystemsto obtainfulldiversity.Further， since the pilots inserted in DD do ? main are also spread to all the TF resource elements， the equivalent DD channels obtained by channel estimation have the average chan ? nelgain.Due todelayandDop ? pler spread， the received symbolsin DD domain are interfered withtheneighboringsymbols.There? fore， the main challenges for OT? FS systems focus on the OTFS re ? ceiver，whichneedstodesign verylowcomplexitydetectors， while the OTFS transmitter is rel? atively simple， as it only needs toadd ISFFT operation before OFDM modulation.

3 OTFS Signal Detector Structures

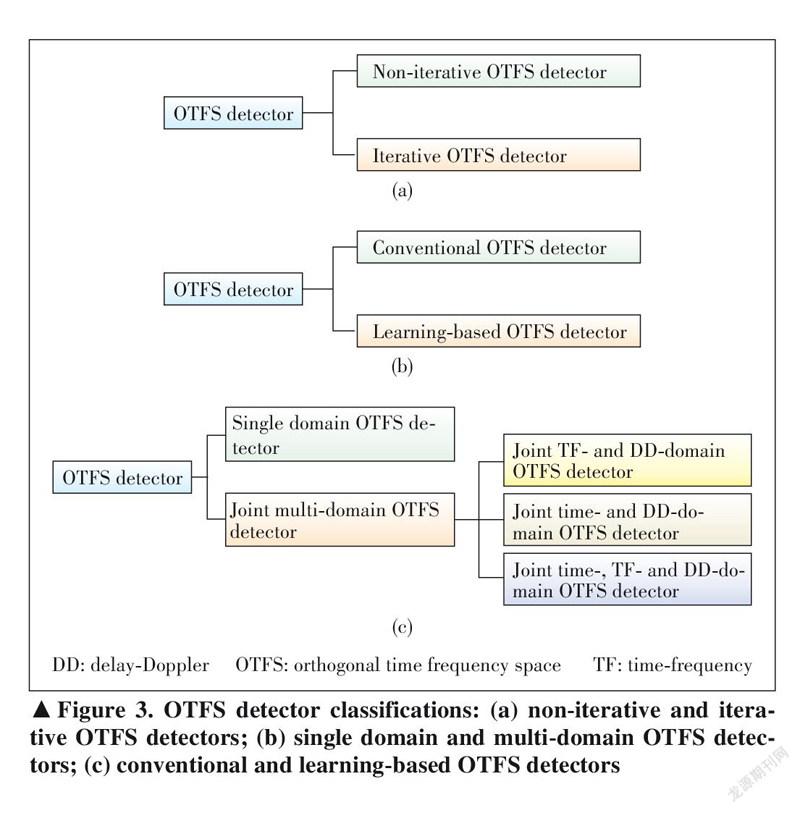
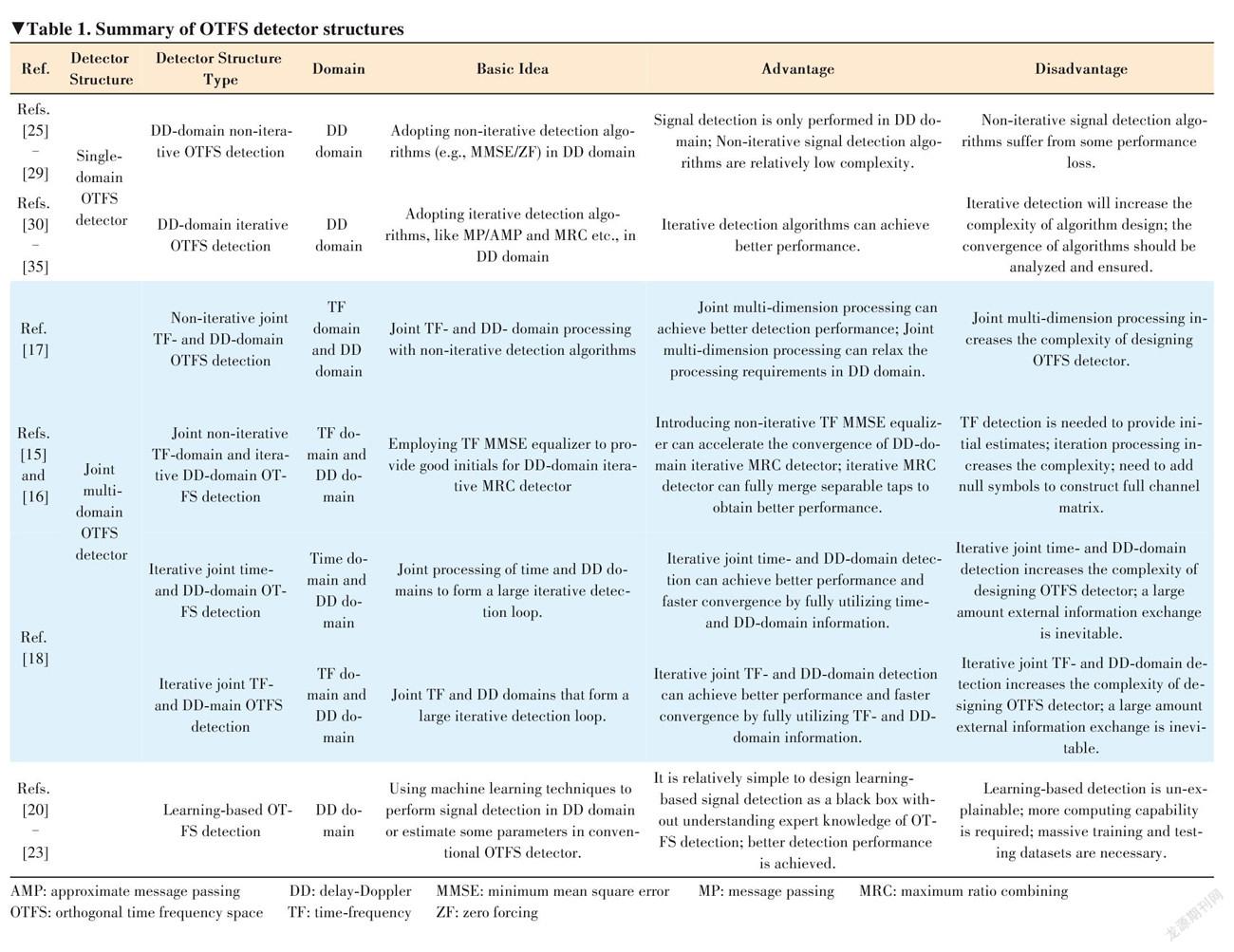
Several works have been devot? ed to studying low complexity OT? FSdetectors.Fig.2illustrates severalpopularOTFSdetector structures，includingDD-domain non-iterativedetector[25 –29]，DD-domain iterative detector[30 –35]， non-iterative joint TF- and DD- domain detector[ 17] ， joint non-iterative TF-domain and iterative DD-domaindetector[15 – 16] ，iterativejointTime-andDD-do? maindetector[ 18] ，iterativejointTF-andDD-maindetector， and learning-enabled detector[20 –23]. According to the number of domains involved in detection processing， these OTFS de? tectors can be divided into two categories： the single-domain OTFSdetectorand jointmulti-domainOTFSdetector.With the need of iteration， these OTFS detectors can be divided into the non-iterative OTFS detector and iterative OTFS detector. These OTFS detectors can also be divided into the convention ? al OTFS detector and learning-based OTFS detector. The de? tailed classifications of OTFS detectors are shown in Fig. 3. A summary of OTFS detectors is illustrated in Table 1.

The DD-domain non-iterative OTFS detector shown in Fig. 2（a） achieves signal detection in the DD domain by using non- iterative detection algorithms like MMSE/ZF， spherical detec ? tion， maximum likelihood （ML） detection， etc.， where MMSE/ ZF is popular and has also been adopted by 4G/5G systems due to its low complexity， while spherical detection and MLdetection are very complex. In general， the DD-domain non-it? erative signal detector adopts MMSE/ZF algorithms. Without iteration operation， the computational complexity and process ? ing delay of MMSE/ZF are small， but at the cost of detection performance loss.

The DD-domain iterative OTFS detector shown in Fig. 2（b） also achieves signal detection in the DD domain， but uses iter? ativedetectionalgorithmslikeMPanditsimprovedalgo ? rithms， and the EP algorithm[39]. These algorithms iteratively updateinformationtoachievebetterdetectionperformance. However， the iteration operation brings some extra computa? tionalcomplexity.Additionally，theconvergenceof iterative detection algorithms needs to be considered. In Ref. [39]， the iterative EPalgorithmand its improvement named Approxi ? mate EP （AEP） were studied. They exhibit better bit error rate （BER） performance than MMSE， MP， MRC rank and VB algo? rithms.

The non-iterative joint TF- and DD-domain OTFS detector shown in Fig. 2（c） can be considered as an improvement of the DD-domain non-iterativeOTFSdetector， which utilizes both TF- and DD-domain information to improve the detection per? formance. In Ref. [ 17]， a sliding window-assisted MMSE （SW- MMSE） equalization in the TF domain was studied， and a DD equalizer likedecision feedbackequalizer（DFE） wasintro? duced. The computation complexity of this non-iterative two- stageequalizerislowerthanconventionalMMSE，andthe BER performance is also better than conventional MMSE.

The joint non-iterative TF-domain and iterative DD-domain OTFS detector shown in Fig. 2（d） can be regarded as an im ? provementoftheDD-domainiterativeOTFSdetector，in whichthenon-iterativeTF-domainequalizerprovidesgood initials for the iterative DD-domain OTFS detector to improve its convergence performance. In Refs. [15] and [ 16]， an itera? tive MRC detector with initial estimates from the output of TF- domain MMSE equalizer was studied， as shown in Fig. 4. The results show that the iterative MRC detector with initial esti ? mates can achieve better BER performance than that without TF-domain MMSE equalization， iterative MPA or MMSE. Con? sidering spatial correlation at the receiver antennas， a sample- based method to estimate such correlation and the optimized combining weights for MRC from the estimated correlation ma? trix were studied in Ref. [42].

Theiterativejointtime-andDD-domainOTFSdetector shown in Fig. 2（e） forms a large iteration loop among the time domainandDDdomain， whichisexpected toobtainbetter performance and lower computational complexity by exploit? ing time domain channel sparsity and DD domain symbol con ? stellation constraints. In Ref. [ 18]， the iterative joint time- and DD-domain signal detector was studied， which adopted an L- MMSE estimator in the time domain and a symbol-by-symbol detection in the DD domain. The results show that this itera? tive joint time- and DD-domain signal detector could achieve almost the same error performance as the maximum-likelihoodsequence detection even in the presence of fractional Doppler shifts， and the computational complexity associated with the domain transformation was low.

The iterative joint TF- and DD-main OTFS detector shown in Fig. 2（f） can be regarded as an improvement of non-iterative joint TF- and DD-main signal detector. Similar as the iterative joint time- and DD-domain OTFS detector shown in Fig. 2（e）， the iterative joint TF- andDD-mainsignal detector formsa largeiterationloopamongtheTFdomainandDDdomain， which is expected to obtain better performance and faster con ? vergencebyutilizing TF-andDD-domaininformation.Fur? thermore， based on the OTFS detector shown in Fig. 2（f）， an it? erative joint time-， TF- and DD-main OTFS detector with time- domain equalization is shown in Fig. 2（g）.

The learning-enabled OTFS detector shown in Fig. 2（h） us? esadvancedmachinelearningmethodtoimprovedetection performance. In Ref. [20]， to reduce the complexity of conven ? tional MP detector in OTFS systems， a damped generalized ap ? proximatemessagepassing（GAMP）algorithmwasstudied and deep learning （DL） was introduced to optimize damping factors.ItsBERperformancecanoutperformtheclassical GAMP algorithm and MP algorithm. In Ref. [21]， a two-dimen? sional convolutional neural network （2D-CNN） based detector was studied to replace the conventional OTFS detector， and an MP-based data augmentation（DA） tool was employed to en? large the training features of the input dataset and mitigate the effect of the channel variations to some degree， leading to im? provement of the robustness and learning ability of the deep neuralnetwork（DNN）.This2D-CNNbaseddetectorcan achieve superior performance compared with the MP detector and similar performance as the MAP detector with a very low complexity. In Ref. [22]， a DD-domain symbol-level DDN de? tector was studied， which could achieve similar BER performance as the full DDN detector and ML detector in static mul ? tipath channel with Gaussian noise， while it achieved better BER performance than the full DDN detector and ML detector in static multipath channel with non-Gaussian noise. In Ref. [23]， a reservoir computing （RC） -based OTFS detector was studied， in which one-shot online learning was sufficiently flexible to cope with channel variations among different OTFS frames and explicit CSI was not required.

4 OTFS Detection Algorithms

OTFS detection algorithms include linear MMSE/ZF， MP and its improvements， MRC， MAP， EP， and VB algorithms. A summary of these detection algorithms including their compu ? tational complexity and BER performance is presented in Ta? ble 2.

4.1 Linear MMSE/ZF Detection Algorithm

Linear signal detection mainly includes MMSE and ZF， while MMSE has been adopted by 4G/5G OFDM systems， due to its low complexity. The detection matrices of classical MMSE and ZF in OTFS systems are GMMSE= （HH H + σ2 Ι ）- 1HHand GZF= （HH H ）- 1HH， respectively. However， when these classical MMSE and ZF detection algorithms are used for OTFS systems directly， they suffer from very high complexity Ο（M3 N3 ）. This is because the number of dimen? sions of equivalent DD channel matrix is MN × MN in OTFSsystems， which results in MN × MN matrix inversion. To re? duce the complexity of linear signal detection in OTFS sys ? tems， considering the sparsity and the block circulant nature of equivalent DD channel， some low complexity linear signal detection schemes have been studied.

In Ref. [27]， the eigenvalues of GMMSEwas computed from the eigenvalues of DD channel matrix H， which can signifi? cantly reduce the complexity. This MMSE with low complexity is summarized as follows：

1） Compute the eigenvalues of each block of H， by comput? ing DFTs of the first row of each circulant block;

2） Compute the eigenvalues of H;

3） Compute the eigenvalues of GMMSE， by using the eigenval? ues of H;

4） Compute GMMSEy.

This idea was also adopted by Ref. [28] to study the detec? tion in MIMO-OTFS systems. Unlike the SISO-OTFS channel， the eigenvalue matrix D in MIMO-OTFS channel is not diago? nal， however， the inverse of the DAconstructed by the matrix D can be performed block-wise by two steps： matrix partition? ing and backtracking[28].

The computational complexity of MMSE is mainly caused by large matrix inversion. Considering the sparsity of equiva? lent DD channel matrix and quasi-banded structure of matri? ces in MMSE detection， a lower-upper （LU） factorization- based low complexity MMSE detection algorithm was studied for OTFS systems with reduced CP[25] and full CP[29]， in which high complexity channel inversion is replaced by low complex ? ity LU factorization operation. Further， the final estimate sym ? bols step can be performed by Fast Fourier Transform （FFT）. Its detailed procedure is illustrated in Fig. 5.

There are some other low complexity MMSE/ZF detection algorithms. For example， the one-tap MMSE detection algo? rithm studied in Ref. [26] achieved low complexity detection in pulse-shaped OTFS systems over doubly-dispersive chan? nels， which only estimated the channel main diagonal and the self-interference power instead of interference cancellation and considered the power of the channel estimation error and self-interference as additional tuning variance parameters.

4.2 MRC Detection Algorithm

The MRC detection algorithm extracts received multipath components of the transmitted symbols in the delay-Doppler grid and combines them by using MRC to improve the signal- to-noise ratio （SNR） of the combined signal. The detailed steps of MRC algorithm are shown as follows[15 – 16]：

1） Construct circulant matrix having element Km，l， accord? ing to the channel Doppler spread vector at each delay tap;

2） Construct matrix R by using a circulant matrix， where Rm=i }Km（H）+ l，l Km + l，l ， m = 0， 1，...，M - lmax;

3） Construct the equations for the symbol vector estimates blm， by using the estimates of symbol vectors from previous iter? ation;

4） Construct gm according to Km + l，l and blm;

5） Perform MRC of the estimates and obtain the output of the maximal ratio combiner， cm= R m（-）1 ? gm ;

6） Estimate all information symbol vectors by ML criterion;

7） Stop criteria by stopping iteration， when some conditionsare satisfing， e.g.， the number of iterations is up to the maxi? mum number of iterations.

4.3 MP Detection Algorithm and Its Improvements

The MP algorithm[30 –32] uses graphical models to decom ? pose a hard problem into several easy sub-problems and itera? tively solve them by passing messages between different types of nodes. The detailed processing steps of an MP algorithm are shown as follows[32]：

1） Message passings from observation nodes to variable nodes： Observation nodes compute the mean and variances of Gaussian random variables and pass them to variables nodes;

2） Message passings from variable nodes to observation nodes： Variable nodes update the probability mass function （PMF） of the alphabet and pass them to observation;

3） Convergence indicator： The convergence indicator is computed;

4） Update decision： The decision on the transmitted sym ? bols is updated， if needed;

5） Stopping criteria： The iteration is stopped when some conditions are satisfing. Note that different stopping criteria will affect convergence and the number of iterations.

Popular MPA detectors still suffer from high complexity and high storage requirements， as well as error floor of BER performance at high SNRs. To further improve the MPA detec ? tor， a matched-filtering based message passing detector with probability clipping （MF-PC-MPD） for OTFS systems was studied in Ref. [33]. MF-PC-MPD first performs matched fil? tering on received OTFS signals， and then uses probability clipping to redistribute the probability if the probability distri ? bution satisfies a certain condition， which makes the symbol variance fluctuate within a certain range and close to each oth ? er; in this way， the Gaussianity is retained.

In Ref. [34]， a Gaussian approximate message passing （GA-MP） detection was studied， which aimed at overcoming the performance degradation of MP detectors causedby non-ideal Gaussian interference due to the limited number of interfering symbols for a certain symbol. The GA-MP detector modeled the individual transmit signals by Gaussian distri? butions， rather than approxi? mating the ISI. This detector outperforms the classical MP detector by at least 1.5 dB at a BER of 10?4， with the same complexity order.

To overcome the performance loss of MP detector in the case of rich scattering environments or fractional Doppler shifts， a unitary approximate message passing （UAMP） detec? tor was studied in Ref. [35]. Considering the equivalent DD channel is a block circulant matrix with circulant blocks which can be diagonalized using a 2D DFT matrix， the UAMP detector performs unitary transform by using a unitary matrix after receiving DD signals. As a result， the UAMP detector al? lows more efficient implementation with the FFT algorithm， and can achieve better BER performance than VB， MRC， MP， and AMP algorithms.

In Ref. [36]， fractionally spaced sampling （FSS） was intro? duced to the OTFS receiver， which can be equivalent to a SI? MO system， and then iterative combining message passing （IC? MP） and turbo message passing （TMP） detectors were studied， by exploiting the sparsity of DD channel and the channel di ? versity gain via FSS. The ICMP detector combines two receiv ? ing channels and then performs message passing iteratively with the Gaussian approximation of the interference compo ? nents. Considering there are two receiving channels in the FSS receiver， the TMP detector uses two individual MP equal? izers with extrinsic log-likelihood ratios （LLRs） exchanging to form a turbo receiver.

The MP detection algorithm is based on the factor graph be ? tween variable nodes and observation nodes， and is very effi? cient for the sparse channel. However， its complexity will be increased when there are a large number of paths such as multi-antenna transmission. To overcome this challenge for OTFS systems with multi-antennas， a joint MP and MRC de? tection algorithm was studied in Ref. [37]， which separated the Doppler frequency offsets （DFOs） in the spatial domain with a beamforming network to ensure the equivalent sparsity and ob ? tained the best diversity by employing MRC to combine all beamforming branches. The main steps in each iteration of the joint MP-MRC algorithm are： 1） Each observation node passes the mean and variance of the interference terms to the con ? nected variable nodes; 2） Each variable node updates thePMF of alphabet symbols and then passes it back to the con ? nected observation nodes; 3） The joint convergence indicator of all beamforming branches is calculated in the MRC fashion after each iteration. Finally， when the convergence is satisfing， the soft output of each transmitted symbol is computed， fol? lowed with hard decision.

4.4 MAP Detection Algorithm

The MAP detection algorithm uses all received signals to es ? timate all transmitted symbols， which can be formulated as= arg max Pr （x|y，H ）. Obviously， its complexity increases withexponent in NM[32]. To reduce the complexity， a near-optimal symbol-wise MAP detection algorithm was studied in Ref. [38]， and its detection rule is expressed as x （k，l） = arg max Pr （x （k，l）|y，H ）.x （k，l） ∈Α

4.5 EP Detection Algorithm

The OTFS system can be represented by a sparsely-connect? ed factor graph where each variable node （VN） is connected to factor nodes D. The main idea of EP algorithm[39] is to use a Gaussian distribution through distribution projection to ap ? proximate the sophisticated posterior distribution in the mes ? sage updating steps， which leads to the complicated belief computation being replaced by means and variances computa? tion. The detailed steps of EP algorithm are represented as fol ? lows[39]：

1） Compute the joint distributionp（xDD ，yDD）;

2） Compute the likelihood functionp（yb |xDD）;

3） Compute the means and variances passed from FNs and VNs as uf（i）b- >xaand vf（i）b- >xa ;

4） Compute the means and variances passed from VNs and FNs as uixa- >fband vixa- >fb;

5） Compute the a posteriori LLR of each coded bit as c a（q）;

6） Stop criteria by stopping iteration， when some conditions are satisfied.

Note that the main computational complexity of the EP algo ? rithm depends on the number of non-zero elements D of chan? nel matrix. In case of rich scattering scenarios and fractional Doppler shift， D is relatively large. To further reduce the com ? putational complexity， small channel coefficients can be ap ? proximated to a fixed value （e.g.， the median value of these small elements） during the message passing from FNs to VNs， which is named channel coeffificients-aware approximate EP （AEP） algorithm[39].

4.6 VB Detection Algorithm

The optimal MAP detection algorithm suffers from very high complexity， which increases exponentially with the size of data symbol vector. To reduce the complexity of MAP algo ? rithm， a variational Bayes algorithm was studied in Ref. [40]. The main idea of VB algorithm is to find a distribution q（d） from a tractable distribution family as an optimized approximation of the a posteriori distribution p（d|y）. The detailed proce? dures are shown as follows：

1） Formulate the approximation q*（d） as an optimal problem by minimizing the Kullback-Leibler divergence;

2） Construct the approximation q（d） by mean filed approxi? mation as q （d ） = ∏k，lqk，l （dk，l ）. Note that in this form， all vari? ables are mutually independent;

3） Transformp（d|y） into a pairwise form;

4） Obtain the variational function in the optimization prob ? lem in Step 1， by substituting q（d） andp（d|y） into the optimiza? tion problem;

5） Find a stationary point of the variational function， by iter? atively updating each local function qk，l （dk，l ）;

6） Approximate a posteriori distributions for all the data symbols iteratively， resulting in the approximate marginals q* k，l （dk，l ）;

7） Estimate the transmitted symbols by finding the maxi ? mum of marginal distribution q* k，l （dk，l ）.

5 HybridOFDM-OTFSMulti-Waveform Detector Structure

To satisfy the requirements for various scenarios and appli ? cations， mobile communication systems have evolved from sin ? gle waveform to multi-waveform systems. For example， in 4G systems， high-spectrum efficiency CP-OFDM is adopted by the downlink， while the uplink adopts single-carrier frequency division multiple access （SC-FDMA） with a low peak to aver? age power ratio （PAPR）. In 5G systems， the downlink adopts CP-OFDM， while CP-OFDM and discrete Fourier transform- spread orthogonal frequency-division multiplexing （DFT-s- OFDM） with low-PAPR are adopted by the uplink. In general， when UE is in the cell center， UE can still obtain the expected QoS with low transmit power， thus UE can adopt CP-OFDM waveform with higher spectrum efficiency. When UE is at the cell edge， UE should increase transmit power to obtain the ex? pected QoS， which requires UE to adopt DFT-s-OFDM wave? form with low PAPR. Since OFTS exhibits excellent perfor? mance in high mobility environments， if OTFS is accepted by future mobile communication systems （FMCS）， its downlink waveform will be CP-OFDM or OTFS， while its uplink wave? form will be CP-OFDM， DFT-s-OFDM or OTFS. To determine each users uplink （UL）/downlink （DL） waveform， the base station shall call UL and DL waveform decision algorithms with the input of user mobility speed and user type. Further， the base station also needs to dynamically switch users down? link and uplink waveform type if some conditions are trig? gered.

Fig. 6 shows the hybrid OFDM-OTFS multi-waveform detec? tor structure， in which Fig. 6（a） is for single user OTFS sys? tems and Fig. 6（b） is for multi-user OTFS systems. The base station first determines the DL and UL waveform types according to certain algorithms with the input of user mobility speed and user type. And then such waveform information is carried by the RRCReconfiguration message and is configured to UE through the air interface. As a result， the base station and UE perform the same waveform processing. Comparing single user hybridOTFS-OFDMsystemsandmulti-userhybridOTFS- OFDM systems， the main difference and difficulty are in the base station. In multi-user hybrid OTFS-OFDM systems， since thebasestationsupportsmulti-usertransmissionandusers may adopt different waveforms， the base station should have the capability of processing multiple waveform in parallel.

Fig. 7 shows the downlink wave ? form selection procedure， which will select CP-OFDM or OTFS ac ? cording to users mobility speed. Since OTFS does not show excel? lent performance in low mobility， the downlink adopts CP-OFDM waveform when users mobility speed is lower than a certain speed threshold， otherwise， the downlink adopts OTFS waveform.

Fig. 8 shows the uplink wave? form selection procedure， which will select CP-OFDM， DFT-s-OFDM or OTFS according to us ? ers mobility speed and user type. Since UE has strict require ? ments for waveforms PAPR， the uplink adopts DFT-s-OFDM with low PAPR when UE is a cell edge user （CEU）. When UE is a cell center user （CCU）， the uplink adopts CP-OFDM waveform if us ? er mobility speed is lower than a certain speed threshold， other? wise， the uplink adopts OTFS waveform.

Considering  multi-user  and multi-waveform  communication systems， the base station needs to simultaneously process multiple users with different waveform types， which requires to design multiple access for multi-wave? form multi-user systems. Taking downlink transmission for an ex? ample， Fig. 9 shows two multiple access schemes for downlink hy? brid OFDM-OTFS multi-user sys? tems. In Fig. 9（a）， the resource of each user allocated in the TF do ? main is orthogonal and OTFS usersresource in the DD domain is also orthogonal， which can effectively avoid inter-user interference. In Fig. 9（b）， the T-F resource are firstly divided into two parts， in which one part is forCP-OFDMusersandtheotherpartisforOTFSusers. Then， CP-OFDM users occupy different T-F resources; while OTFS users are spread in the total T-F resources allocated to all the OTFS users， each OTFS user is orthogonal in the DD domain. Comparing the schemes shown in Figs. 9（a） and 9（b）， OTFSusersinFig.9（a）suffer fromlessinter-userinterference，astheyareorthogonalinbothDDandT-Fdomains. However， their diversity gain is also lower than that in Fig. 9（b）， as diversity gain of OTFS modulation is positively related with the number of resources.Obviously， the number of re? sources allocated to each OTFS user in Fig. 9（a） is less than that in Fig. 9（b）. For UL multi-waveform multi-user systems， they are similar as the downlink situation.

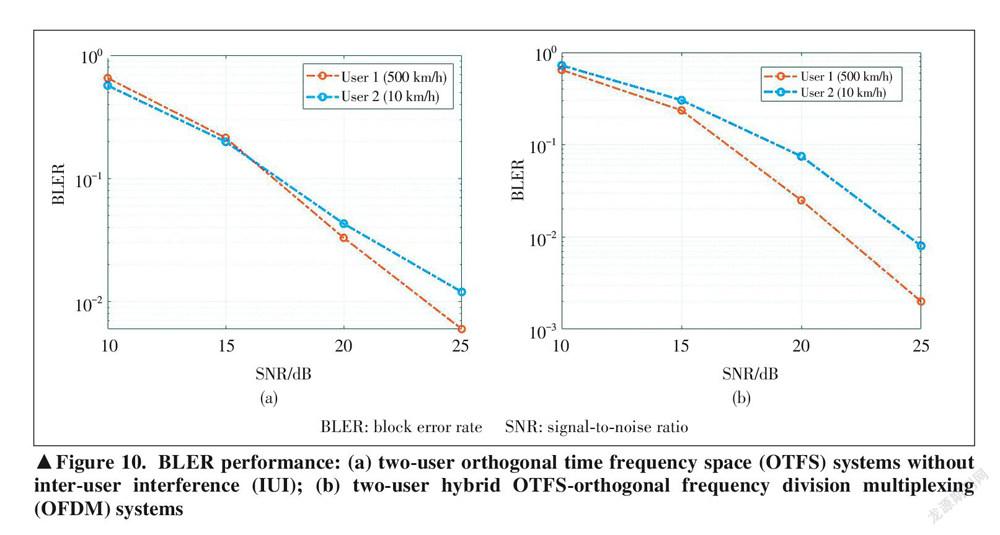
Fig.10 shows the block error rate （BLER） performance of two-userOTFSsystems withoutinter-userinterference（IUI） and two-user hybrid OTFS-OFDM systems in fractional Dop ? pler channels， where the speed of User1 is 500 km/h， while the speed of User 2 is 10 km/h. In Fig. 10（a）， both User 1 and User 2 adoptOTFS modulation， while in Fig.10（b）， User1 adoptsOTFS modulation but User2adoptsOFDMmodula? tion.TheresultsshowthattheOTFSmodulationcannotachieve dramatic BLER performance gain in a low-speed sce? nario while some BLER performance gain can be obtained in a high-speed scenario. Therefore， it is suggested that low-com? plexityOFDM modulation is used to low-speed users， while high-speed users adopt OTFS modulation. Since different us ? ers withdifferentspeedscoexistin thebasestation， hybrid OTFS and OFDM systems should be considered.

6 Main Challenges and Future Research Di? rections

6.1 Main Challenges

6. 1. 1 Low Complexity OTFS Detection Algorithms

InOTFSsystems，NMsymbolsintheDDdomainare spreadtotheTFdomainbyemployingISFFTtransform， which results in the large number of dimensions of the equiva? lent DD channel. Furthermore， with the introduction of multi- antenna transmission， the complexity of OTFS detection will also increase dramatically. According to current research re ? sults， the minimum computational complexity of OTFS detec ? tor is Ο（MNlog （N ） ）. Obviously， the computational complexi ? ty of OTFS detector is still far higher than that of OFDM detec ? tor. As a result， current OTFS detection algorithms cannot sat? isfy the requirements forOTFSsystems. Additionally， manyworks assume that the DD channel matrix is block circulantandsparse.However，asshowninsome works，if therearerich scattering or a large number of paths such as MIMO-OT ? FS systems， the block circulant and sparsity will not be satisf? ing. Furthermore， integer Doppler shifts are assumed in many works，whiletheassumptionof fractionalDopplershiftsis more reasonable in practical OTFS systems. However， fraction? al Doppler shifts will increase computational complexity and resultinmoreseriousinter-Dopplerinterference. Therefore， the research on low complexity OTFS detection algorithm is a great challenge.

6. 1.2 Decoupling Between MIMO-OTFS Detector and Precoder

CurrentresearchonOTFSreceiversmainlyfocuseson SISO-OTFS systems， while just a few works study MIMO-OT ? FSsystems.However， when extendingSISO-OTFS detection algorithmstoMIMO-OTFSsystems，itwillfacesomenew problems. For example， when the MRC detector is used to MI? MO-OTFSsystems，it needs toobtain the precodingmatrix. However，whenanon-codebook-basedprecodingschemeis adopted， it is difficult for the OTFS receiver to obtain the pre ? coding matrix. That is， in order to match the detection algo ? rithms，some detectors requirespecial design at theMIMO- OTFS transmitter side. Thisstrongcouplingdesign between the MIMO-OTFS receiver and transmitter reduces the flexibili ? ty of MIMO-OTFSsystemdesignand processing. Therefore， theresearchonMIMO-OTFSdetectorsanddetectionalgo ? rithms， which is decoupled with the MIMO-OTFS transmitter， is another challenge.

6. 1.3 Multi-Waveform Hybrid OTFS Detector

OTFS modulation can obtain delay-Doppler diversity gain， and thus it can achieve better performance than conventional OFDMsystemsinhighmobilityscenarios. However，OTFS modulation cannot obtain obvious performance gain in low mo ? bility scenarios. When users experience different scenarios， it wouldbebettertoswitchwaveformtoobtainbetterperfor? mance.Thecoexistenceofmultiplewaveforms，suchas OFDM and OTFS， requires that the receiver supports multi-waveform processing and wave ? form switching， which increases the complexity of the receiver. Therefore， designing a low com ? plexity unified multi-waveform re? ceiver is also a challenge.

6.2 Further Research Direc ? tions

6.2. 1 Advanced Low Complexity OTFS Detectors and Detec ? tion Algorithms

The computational complexity of current OTFS detection algo ? rithms has been reduced toO（MNlog （N ） ），butitisstill much higher than the acceptable complexity in practical sys ? tems. Therefore， in the future， the first important work is to study advanced low complexity OTFS detector structures and detectionalgorithms.AsforOTFSdetectorstructures，even though some single domain and joint multi-domain OTFS de? tectors have been studied， there are still some novel OTFS de ? tector structures to be studied such as joint channel estimation and detection. As for OTFS detection algorithms， some non-it? erative and iterative detection algorithms have been studied， but their computation complexities are still very high， up to Ο（MNlog （N ） ）. The properties of DD channel matrix together withsomesimplifiedandapproximatedmatrixoperations should be further exploited to develop novel OTFS detection algorithms.Furthermore，iterativedetectionalgorithmscan achieve better performance， but they are needed to further an? alyze the convergence by employing some tools such as extrin ? sic information transfer （EXIT） chart and design efficient itera? tion stopping schemes to reduce the number of iterations.

6.2.2 Learning-Based OTFS Detectors

Several OTFS detection algorithms have been studied， but theyreducethecomputationalcomplexitybyexploitingthe block circulant and sparsity， as well as simplified and approxi ? mated mathematical methods. It will become more difficult to find more low complexity OTFS detection algorithms. A learn? ing-based method provides a new way for the OTFS detector， whichconsidersOTFSdetectionprocessingasablackbox andperformsOTFSdetectionbydeployingonlinelearning model trained offline. Currently， there are few research works on learning-basedOTFS detector， and thus many efforts are needed to study learning models and performance verification. Therefore，thelearning-basedOTFSdetectorisa futurere ? search direction.

6.2.3 Unified Multi-Waveform Detector Design

If OTFS modulation is adopted， the downlink and uplink of future mobile communication systems will be multi-waveform.However， there are few works to study the receiver design to support coexistence of multiple waveform. To support multi- waveformsystems， the receiver shouldsupport signal detec ? tion of each waveform. A simple way is to deploy multiple sig? naldetection modules and switch among these detection mod ? ulesaccordingtoconfiguredwaveformtype. However，this way is inefficient and will increase the processing complexity. A better way is to design a unified multi-waveform receiver， which can flexibly and efficiently support signal detection of different waveform. Therefore， unified multi-waveform receiv? er design is another future research direction.

7 Conclusions

In this paper， the research works on low complexity OTFS detectorshavebeensurveyedcomprehensively. Firstly，we presenttheOTFSsystemmodelandbasicprinciples. And then， we focuson lowcomplexityOTFSdetectorstructures， and give the categories and discussions of all surveyed OTFS detector structures. According to different classification regu ? lations， two classifications of OTFS detectors are the single-do? mainOTFSdetectorand jointmulti-domainOTFSdetector; the non-iterative OTFS detector and iterative OTFS detector. As for their performance， the joint multi-domain OTFS detec ? tor is superior to the single-domain one， while the iterative OT? FS detector is better than the non-iterative one. We also pro? vide an overview on the principles of popular OTFS detection algorithms， and discuss them in terms of complexity and per? formance. Furthermore， considering the coexistence of multi ? ple waveforms such as OTFS and OFDM， we discuss the de? sign forhybridmulti-waveformdetectorsinsingleuserand multi-user OTFS systems， and waveform switching procedures andalgorithms. Finally， we present mainchallenges for low complexity OTFS detectors and identify some future research directions.

References

[ 1] ITU-R. Framework and overall objectives of the future development of IMT for 2020 and beyond： ITU-R M.2083-0 [R]. 2015

[2] 3GPP. Study on NR vehicle-to-everything （V2X） （Release 16）： 3GPP TR 38.885 [R]. 2019

[3] CHEN S Z， HU J L， SHI Y， et al. Vehicle-to-everything （v2x） services supported by LTE-based systems and 5G [J]. IEEE communications standards magazine， 2017， 1（2）： 70 –76. DOI： 10. 1109/MCOMSTD.2017. 1700015

[4] 3GPP.Mobilecommunicationsystemforrailways（Release17）：3GPPTS 22.289 [S]. 2019

[5] AI B， GUAN K， RUPP M， et al. Future railway services-oriented mobile commu ? nications network [J]. IEEE communications magazine， 2015， 53（10）： 78 – 85. DOI： 10. 1109/MCOM.2015.7295467

[6] ZHANG Z Q， XIAO Y， MA Z， et al. 6G wireless networks： vision， requirements， architecture，andkeytechnologies[J].IEEEvehiculartechnologymagazine， 2019， 14（3）： 28 –41. DOI： 10. 1109/MVT.2019.2921208

[7] FAN P Z， ZHAO J， I C L. 5G high mobility wireless communications： challenges and solutions [J]. China communications， 2016，13 （Supplement 2）：1 – 13. DOI： 10. 1109/CC.2016.7833456

[8] HADANI R， RAKIB S， TSATSANIS M， et al. Orthogonal time frequency space mod ? ulation[C]//IEEE WirelessCommunications and NetworkingConference（WCNC）. San Francisco， USA： IEEE， 2017： 1 –6. DOI： 10.1109/WCNC.2017.7925924

[9] WEI Z Q， YUAN W J， LI S Y， et al. Orthogonal time-frequency space modula? tion： a promising next-generation waveform [J]. IEEE wireless communications， 2021， 28（4）： 136 – 144. DOI： 10. 1109/MWC.001.2000408

[ 10] 3GPP TSG RA WG1. Overview of OTFS waveform for next generation RAT： Meeting #84-bis R1162929 [R]. Busan， South Korea： 3GPP， 2016

[ 11] 3GPP TSGRA WG1.OTFS modulation waveformand referencesignals for new RAT： Meeting #84-bis R1162930 [R]. Busan， South Korea： 3GPP， 2016

[ 12] 3GPP TSG RA WG1. Performance results for OTFS modulation： Meeting #85 R1165620 [R]. Nanjing， China： 3GPP， 2016

[ 13] MobileChina. White paper on 2030+ technology trends [R]. 2019

[ 14] JING L Y， WANG H， HE C B， et al. Two dimensional adaptive multichannel decision feedback equalization for OTFS system [J]. IEEE communications let? ters， 2021， 25（3）： 840 – 844. DOI： 10. 1109/LCOMM.2020.3039982

[15] THAJ T， VITERBO E. Low complexity iterative rake detector for orthogonal timefrequencyspacemodulation[C]//IEEEWirelessCommunicationsand NetworkingConference（WCNC）.Seoul，Korea（South）：IEEE，2020：1– 6. DOI： 10. 1109/WCNC45663.2020.9120526

[ 16] THAJ T， VITERBO E. Low complexity iterative rake decision feedback equal ? izer for zero-padded OTFS systems [J]. IEEE transactions on vehicular technol? ogy， 2020， 69（12）： 15606 – 15622. DOI： 10. 1109/TVT.2020.3044276

[ 17] JIN C X， BIE Z S， LIN X H， et al. A simple two-stage equalizer for OTFS with rectangular windows[J]. IEEE communications letters， 2021， 25（4）：1158– 1162. DOI： 10. 1109/LCOMM.2020.3043841

[ 18] LI S Y， YUAN W J， WEI Z Q， et al. Cross domain iterative detection for or? thogonal time frequency space modulation [J]. IEEE transactions on wireless communications， early access. DOI： 10. 1109/TWC.2021.3110125

[ 19] SHAN Y R， WANG F G. Low-complexity and low-overhead receiver for OTFS via large-scale antenna array [J]. IEEE transactions on vehicular technology， 2021， 70（6）： 5703 –5718. DOI： 10. 1109/TVT.2021.3072667

[20] XU X K， ZHAO M M， LEI M， et al. A damped GAMP detection algorithm for OTFS system based on deep learning[C]//IEEE 92nd Vehicular Technology Conference（VTC2020-Fall）.Victoria，Canada：IEEE，2020：1– 5.DOI： 10. 1109/VTC2020-Fall49728.2020.9348493

[21] ENKU Y K， BAI B M， WAN F， et al. Two-dimensional convolutional neural network based signal detection for OTFS systems [J]. IEEE wireless communi? cations letters， 10（ 11）： 2514 –2518. DOI： 10. 1109/LWC.2021.3106039

[22] NAIKOTIA，CHOCKALINGAMA.Low-complexitydelay-dopplersymbol DNN for OTFS signal detection [C]//IEEE 93rd Vehicular Technology Confer? ence （VTC2021-Spring）. Helsinki， Finland： IEEE， 2021： 1 – 6. DOI： 10. 1109/ VTC2021-Spring51267.2021.9448630

[23] ZHOU Z， LIU L J， XU J R， et al. Learning to equalize OTFS [EB/OL]. （2021- 07-17）[2021-08-31]. https：//arxiv.org/abs/2107.08236

[24] PANDEY B C， MOHAMMED S K， RAVITEJA P， et al. Low complexity pre? coding and detection in multi-user massive MIMO OTFS downlink [J]. IEEE transactions on vehicular technology， 2021， 70（5）： 4389 –4405. DOI： 10. 1109/TVT.2021.3061694

[25] TIWARI S， DAS S S， RANGAMGARI V. Low complexity LMMSE Receiver for OTFS [J]. IEEE communications letters， 2019， 23（ 12）： 2205 – 2209. DOI：10. 1109/LCOMM.2019.2945564

[26] PFADLER A， JUNG P， SZOLLMANN T， et al. Pulse-shaped OTFS over doubly- dispersive channels： one-tap vs. full LMMSE equalizers [C]//IEEE International Conference on Communications Workshops （ICC Workshops）. Montreal， Cana? da： IEEE， 2021： 1 –6. DOI： 10. 1109/ICCWorkshops50388.2021.9473535

[27] SURABHI G D， CHOCKALINGAM A. Low-complexity linear equalization for OTFS modulation [J]. IEEE communications letters， 2020， 24（2）： 330 – 334. DOI： 10. 1109/LCOMM.2019.2956709

[28] SINGH P， MISHRA H B， BUDHIRAJA R. Low-complexity linear MIMO-OT? FSreceivers[C]//IEEEInternationalConferenceonCommunicationsWork? shops （ICC Workshops）. Montreal， Canada： IEEE， 2021： 1 – 6. DOI： 10. 1109/ ICCWorkshops50388.2021.9473839

[29] ZOU T T， XU W J， GAO H， et al. Low-complexity linear equalization for OTFS systemswithrectangularwaveforms[C]//IEEEInternationalConferenceonA Survey on Low Complexity Detectors for OTFS SystemsSpecial Topic ZHANG Zhengquan， LIU Heng， WANG Qianli， FAN PingzhiCommunicationsWorkshops（ICCWorkshops）.Montreal，Canada：IEEE， 2021： 1 –6. DOI： 10. 1109/ICCWorkshops50388.2021.9473771

[30] KOLLENGODE RAMACHANDRAN M， CHOCKALINGAM A. MIMO-OTFS in high-doppler fading channels： signal detection and channel estimation [C]//IEEE GlobalCommunicationsConference（GLOBECOM）.AbuDhabi，UnitedArab Emirates： IEEE， 2018： 206 –212. DOI： 10. 1109/GLOCOM.2018.8647394

[31] RAVITEJA P， PHAN K T， JIN Q Y， et al. Low-complexity iterative detection for orthogonal time frequencyspacemodulation[C]//IEEEWirelessCommunica? tions and Networking Conference （WCNC）. Barcelona， Spain： IEEE， 2018： 1 – 6. DOI： 10. 1109/WCNC.2018.8377159

[32] RAVITEJA P， PHAN K T， HONG Y， et al. Interference cancellation and itera? tive detection for orthogonal time frequency space modulation [J]. IEEE trans? actionsonwirelesscommunications，2018，17（ 10）：6501– 6515.DOI：10. 1109/TWC.2018.2860011

[33] ZHANG H J， ZHANG T T. A low-complexity message passing detector for OT? FS modulation with probability clipping [J]. IEEE wireless communications let? ters， 2021， 10（6）： 1271 – 1275. DOI： 10. 1109/LWC.2021.3063904

[34] XIANG L P， LIU Y S， YANG L L， et al. Gaussian approximate message pass ? ing detection of orthogonal time frequency space modulation [J]. IEEE transac? tions on vehicular technology， 2021， 70（ 10）：10999 – 11004. DOI：10. 1109/TVT.2021.3102673

[35] YUAN Z D， LIU F， YUAN W J， et al. Iterative detection for orthogonal time frequencyspacemodulationwithunitaryapproximatemessagepassing[J]. IEEE transactions on wireless communications， early access. DOI：10. 1109/TWC.2021.3097173

[36] GE Y， DENG Q W， CHING P C， et al. Receiver design for OTFS with a frac ? tionally spaced sampling approach [J]. IEEE transactions on wireless commu ? nications， 2021， 20（7）： 4072 –4086. DOI： 10. 1109/TWC.2021.3055585

[37] CHENG J Q， JIA C L， GAO H， et al. OTFS based receiver scheme with multi-an? tennas in high-mobility V2X systems [C]//IEEE International Conference on Com? munications Workshops （ICC Workshops）. Dublin， Ireland： IEEE， 2020：1 – 6. DOI： 10. 1109/ICCWorkshops49005.2020.9145313

[38] LI S Y， YUAN W J， WEI Z Q， et al. Hybrid MAP and PIC detection for OTFS modulation [J]. IEEE transactions on vehicular technology， 2021， 70（7）： 7193 – 7198. DOI： 10. 1109/TVT.2021.3083181

[39] LI H， DONG Y Y， GONG C H， et al. Low complexity receiver via expectation propagation for OTFS modulation [J]. IEEE communications letters， 2021， 25 （ 10）： 3180 –3184. DOI： 10. 1109/LCOMM.2021.3101827

[40] YUAN W J， WEI Z Q， YUAN J H， et al. A simple variational Bayes detector for orthogonal time frequency space （OTFS） modulation [J]. IEEE transactions onvehiculartechnology，2020，69（7）：7976–7980.DOI：10. 1109/TVT.2020.2991443

[41] QU H Y， LIU G H， ZHANG L， et al. Low-complexity symbol detection and in ? terference cancellation for OTFS system [J]. IEEE transactions on communica ? tions， 2021， 69（3）： 1524 – 1537. DOI： 10. 1109/TCOMM.2020.3043007

[42] THAJ T， VITERBO E. Low-complexity linear diversity-combining detector forMIMO-OTFS[J]. IEEE wireless communications letters， 2021， earlyaccess. DOI： 10. 1109/LWC.2021.3125986

Biographies

ZHANG Zhengquan （zhangzqswjtu@163. com） received the Ph. D. degree in information and communication engineering from Southwest JiaotongUniversi ? ty， China in 2019. From 2008 to 2013， he was with ZTE Corporation as a com ? munication engineer. From 2016 to 2017， he was a guest Ph.D. student with the KTH Royal Institute of Technology， Sweden. Since 2019， he has been with the Department of Communication Engineering， School of Information Science and Technology， Southwest Jiaotong University. His research interests include B5G and 6G wireless communication technologies. He is a member of IEEE.

LIU Heng received the Ph. D. degree in information and communication engi ? neering from Southwest Jiaotong University， China in 2013. Since 2013， he has been with the Department of Communication Engineering， School of Informa? tion Science and Technology， Southwest Jiaotong University. His research inter? ests include next-generation wireless communications， rail transit wireless communications， machine learning and intelligent wireless communications.

WANG Qianli received the B. S. and M. S. degrees in electronic and informa? tion engineering and the Ph.D. degree from the University of Electronic Science and Technology of China in 2013， 2016 and 2021， respectively. Since 2021， he has been with the Department of Communication Engineering， School of Infor? mation Science and Technology， Southwest Jiaotong University， China. His re? search interests include estimation theory， array signal processing， radar sensor network， and compressed sensing.

FAN Pingzhi is currently a distinguished professor of Southwest Jiaotong Uni ? versity， China， and a visiting professor of Leeds University， UK （ 1997 –）. He is a recipient of the UK ORS Award （1992）， the National Science Fund for Distin ? guished Young Scholars （ 1998， NSFC）， IEEE VT Society Jack Neubauer Memo ? rial Award （2018）， IEEE SP Society SPL Best Paper Award （2018）， IEEE WC? SP 10-Year Anniversary Excellent Paper Award （2009 – 2019）， and IEEE/CIC ICCC Best Paper Award （2020）. He served as a chief scientist of the National “973”Plan Project between January 2012 and December 2016. He is an IEEE VTS Distinguished Speaker （2019 – 2022）， a fellow of IEEE， IET， CIE and CIC. His research interests include high mobility wireless communications ， massive random-access techniques， and signal design and coding.