基于改进RRT-Connect算法的机械臂抓取路径规划
李磊 吴翔 包祥威 张景涛 方翔 曹毅
(1河南工业大学电气工程学院,郑州,450001;2河南工业大学机电工程学院,郑州,450001)
0 引言
操作臂的避障路径规划是在操作臂的工作空间内完成起止位姿之间安全连续路径搜索,一般以路径最短、搜索时间最短、或者能量消耗最优其中之一作为评价标准。目前按照操作臂所处环境信息已知状态,避障路径规划可分为全局路径规划和局部路径规划。基于全局路径规划的方法主要有自由空间法、构型空间法、拓扑法和栅格法等。基于局部路径规划的方法有人工势场法、遗传算法、模糊逻辑算法、神经网络法、蚁群禁忌搜索算法[1],粒子群算法[2]等等。这些算法有的适合静态环境,有的适用于动态环境,有的搜索速度快但易陷入局部极优,若对一些算法进行改进和结合,可以使改进后的算法达到更理想的效果。
通过对比国内外规划算法研究分析发现[3-4],遗传算法、神经网络等智能仿生学算法应用于三维空间模型避障运动规划较为困难,且搜索效率较低;人工势场法等传统算法容易早熟收敛;多项式轨迹插值拟合计算量大,耗时长;基于随机采样的避障路径规划算法具有强适应性和概率完备性,高维空间避障路径采用随机采样可以有效减少精确建模时间。
基于随机采样的应用最多的算法为概率路标法和快速扩展随机树法。
概率路标法是在操作臂的可行空间内进行随机采样,连接邻近点构建“路标图”,查询路标图中起始位置到目标位置最短可行路径[5]。该方法虽实用性强,但是最终得到的路径可能不是最优路径。
快速扩展随机树法模拟树枝生长产生枝叶进行空间扩展路径搜索,是一种增量式采样算法[6],对于在线和离线路径规划都适用,在高维空间路径规划该算法时效性较好,且具有概率完备性,但每次规划所得路径随机性大,且得到的路径存在不光滑现象。
本文针对传统操作臂避障路径规划算法进行分析比较,选择双树快速随机扩展连接树RRT-Connect算法进行改进,并利用Dijkstra[7]算法和B样条对改进算法规划路径进行优化处理,以达到减少规划路径长度、时间和平滑路径的目的。
1 RRT算法
RRT(快速随机扩展树)算法是一种简单采样算法。为了算法描述方便,引入一些参数,这些参数的意义如表1所示。

表1 RRT算法各参数意义


2 改进RRT-Connect算法

2.1 RRT-Connect算法步骤

2.2 RRT-Connect算法的改进


3 路径优化

3.1 Dijkstra算法
通过 算法搜索最短路径时,首先指定起始节点s,此外引进两个集合S和U。S是用来存放已求出最短路径节点的集合,U是用来存放剩余节点的集合。算法初始时,将起始节点s加入集合S中,并用邻近矩阵D记录各个节点之间距离。通过不断循环寻找U集合中距离起始节点最近的节点,将该节点放入到集合S中,并修改起始节点经过该节点到其他节点的邻近矩阵的值。
在算法中,采用 表示i节点与起始节点s之间的距离,两个节点之间若连通,则w(i,j)表示i节点和j节点之间的权值,否则w(i,j)=∞。根据节点图构造邻近矩阵Dn×n,n表示节点图中节点个数。首先求出邻近矩阵的第一行除去起始节点之外的最小值,并记为k,则第k个节点就是距离起始节点最近的节点,将k节点加入集合S中。然后从集合U中求出距离起始节点最近的节点m,在将m节点加入S集合之前,需要做以下比较:
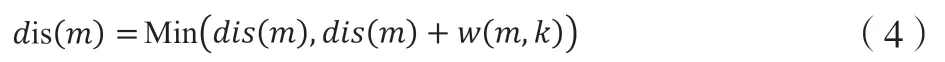
根据式(4)计算出m节点到起始节点的最短距离,并对邻近矩阵D内的值进行替换。依次循环,直至U中节点都加入集合S为止。Dijkstra算法流程图如下;
3.2 路径平滑处理
改进RRT-Connect算法优化后的路径,在节点连接处存在折点、不平滑现象。操作臂沿此路径执行任务时,操作臂会出现快速变向现象,该现象必然会影响执行任务的精度,并减少操作臂的使用周期。为了避免出现这种现象,必须对规划路径进行平滑处理。B样条曲线在路径平滑方面效果显著,其优点之一便是修改局部路径而不会对全部路线变动。
一般情况下,K阶B样条曲线方程可表示为:

本文采用三次B样条对路径进行优化处理,为使操作臂的运动更加平稳,尽可能多地插入平滑路径点。
4 算法验证
为验证本文算法的有效性,笔者进行了算法仿真试验。在每组实验中,起点均用符号‘S’表示,坐标为(10,10),终点均用符号‘G’表示,坐标为(490,490),坐标点单位为cm。实验中各类算法的路径规划结果如图2-图6所示。

图2 原始RRT算法仿真结果
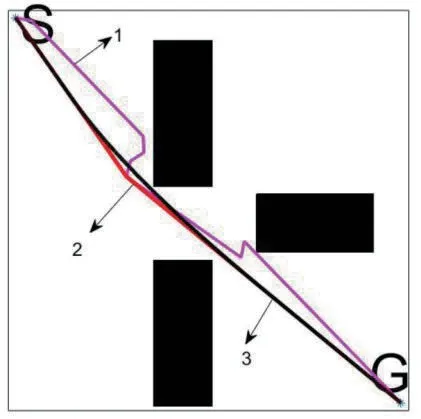
图6 B 样条曲线仿真结果
实验1:原始RRT算法的路径规划。
实验2:在实验1的基础上引入双向搜索策略,采用RRT-Connect算法路径规划策略,并与RRT仿真结果进行对比。
图3中,规划路径分别由1号蓝色路径和2号红色路径拼接组成,3号路径是去除无效节点之后完整规划路径。

图3 RRT-Connect算法仿真结果
为了避免采样算法的随机性误差,进行40次仿真验证,得到验证结果如表2所示。

表2 RRT与RRT-Connect算法仿真结果对比
由表2可知,RRT-Connect算法在平均搜索时间、平均节点和平均路径长度上远远优于原始RRT算法。
实验3:在实验2的基础上采用改进RRT-Connect算法进行路径规划。
图4中,规划路径分别由1号蓝色路径和2号红色路径拼接组成,3号粉红色路径是去除无效节点之后完整规划路径。
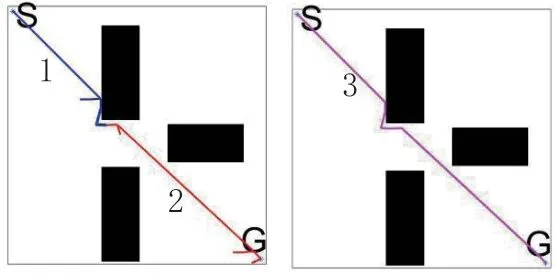
图4 改进RRT-Connect算法仿真结果
由图3和图4对比可知改进RRT-Connect算法减少了了无效节点的出现,且路径长度优于传统RRT-Connect算法。
实验4:在实验3的基础上引入Dijkstra算法搜索最短路径。
图5中,1号红色路径表示优化之后的路径,2号粉红色路径是改进RRT-Connect规划路径。明显看出,红色路径比粉红色路径长度更短。

图5 融合Dijkstra算法仿真结果
为了避免采样算法的随机性误差,进行40次仿真验证,得到验证结果如表3所示。

表3 RRT-Connect与融合算法仿真结果对比
由表3可知,改进RRT-Connect与Dijkstra融合算法IRRT-Connect在平均搜索时间、平均节点和平均路径长度优于改进RRT-Connect算法。
实验5:在实验4的基础上采用B样条曲线对路径进行平滑处理。
图6中,1号粉红色路径表示首次规划路径,2号红色路径表示Dijkstra算法优化路径,3号黑色路径表示B样条函数平滑处理后路径。
由图6中三条路径对比可知,平滑处理后的黑色路径在节点连接处比红色路径曲率更小。
5 仿真实验
仿真实验以越疆科技有限公司生产的Dobot魔术师为机械臂模型进行三维空间路径规划,该机械臂三个自由度。空间环境包括操作臂模型和障碍物模型。
为易于观察,图7所示的规划场景去掉障碍物上面一部分。在X方向上,障碍物中心点与机械臂的距离为25,在Y方向上为25,在Z方向上为0,长度单位均为cm。

图7 操作臂规划场景
在操作臂规划场景内应用改进RRT-Connect算法进行避障路径规划,确定操作臂的起始坐标和目标坐标分别为(20,10,18)和(25,10,20)并在空间中用“start”和“goal”标注。
操作臂完成从起始目标点向目标节点的运动路径规划如下。
首次规划路径如图8中红色路径所示。

图8 操作臂首次规划路径
首次规划路径呈锯齿状,存在多余路径节点,利用Dijkstra算法进行二次路径优化。优化路径如图9中绿色路径所示。

图9 操作臂规划优化路径
虽然优化路径与首次规划路径相比,减少了路径长度,但路径在节点连接处存在折角。采用B样条曲线对路径进行光滑处理,平滑后路径如图10中3号粉红色路径所示。

图1 Dijkstra算法流程图

图10 操作臂规划平滑路径
选取相同的操作臂避障空间环境,分别进行原算法和改进的融合算法路径规划。路径规划结果如图11所示。

图11 算法规划路径对比
在操作臂三维空间配置同样的规划场景,进行RRT算法、RRT-Connect算法和改进RRT-Connect多次仿真验证,取验证平均结果作为对比标准,仿真结果如表4所示。
通过表4可以发现,本文提出的规划算法对串联机械臂的实际使用具有参考价值。

表4 三维空间算法仿真结果对比
6 结论
针对机械臂在抓取目标物体的路径规划问题,本文提出了一种改进RRT-Connect和Dijkstra融合算法的路径规划策略。引入双树目标偏执、极致贪婪策略提高路径搜索速率,减少了传统RRT-Connect算法中无效节点数量、搜索时间和路径长度,再利用Dijkstra算法进行首次路径优化,得到最短路径。为了避免优化后的路径在节点连接处存在折点、不平滑现象,必须对规划路径进行平滑处理,其中利用B样条差值的方法得到一条光滑平缓的完整运动曲线。仿真表明,该算法更加适合机械臂的实际运行与操作,进而证明该算法的可行性与实用性。
本文是在障碍物位置信息已知的情况下,对空间中机械臂的避障轨迹规划进行研究,但在实际应用环境中,障碍物环境位置往往处于未知状态,因此对复杂环境下的机械臂轨迹规划有待进一步研究和改善。

