铺管船管子堆场挡货立柱设计

陆少杰，罗瑞锋，黄曌宇

（上海振华重工（集团）股份有限公司，上海 200125）

0 引言

在铺管船项目中，主甲板管子堆场区域不仅需要考虑堆管的布置，同时也要考虑其他作业需求的设备的布置。在布置堆管区时也要善于利用船体结构的纵-横向筋板作为挡货立柱的反面加强，做到尽可能减少不必要的反面加强。但在这样的考虑情况下，易布置出非均布的挡货立柱。对于这样的超静定结构，本文通过国内某多功能铺管船主甲板堆管区域划分及其最大一跨挡货立柱设计为案例，分析该类结构的有效载荷、应力计算和方案设计方法，结合有限元强度计算对方法进行校核。

1 外载分析

1.1 挡货立柱设计与布置概述

在某最新多功能铺管船上，管子堆场主甲板共约2 000 m2存储面积，甲板载荷w按100 kN/m2[1-2]。以该船挡货立柱的布置、计算及设计过程为案例，介绍铺管船堆场立柱设计方法，同时设计中为达到项目成本上的优化，将考虑采用A级钢（屈服强度为235 MPa）作为设计用钢，并在该方法设计的挡货立柱基础上，通过对其实体建模，配合有限元软件加载，进行方法的有效性复核。

在实际堆场布置中，挡货立柱既要考虑与已有甲板反面加强对筋，又要考虑不与其他专业设备干涉，同时因为占地面积大不排除后期各专业协调产生的移位等可能，故设计阶段首先需准确地载荷分析得出合理的力学简化模型，并在计算过程中通过可变参数的整理进行计算公式的统一，为不同分区的立柱形式以及未来可能的布置移位提供一种快速的设计方法。

1.2 工况分析

以图1堆场布置中最大载货面积的一跨为案例介绍挡货立柱的设计过程。挡货立柱工况如图2所示。

图1 项目管子堆场布置图

根据船体设计规格书可知，船体横向加速度a横为0.65 g，其中g为重力加速度；纵向加速度a纵为0.2 g。而堆管区域为防止甲板磨损均铺设有垫木，其摩擦系数µ为(0.4～0.6) g。

根据图2的工况介绍可知，堆管区实际堆管后除自身重力外，还会因船体纵向与横向的船倾而产生作用力。纵向上因堆场使用的垫木摩擦系数大于船体纵倾加速度，故可以不再设置挡货立柱进行约束。横向上垫木摩擦力较为接近该方向船倾加速度，且实际铺管船作业需要设置边界以便于向甲板垂直向上逐层堆管，故实际布置中考虑将挡货立柱布置在堆场堆管的横向方向上。

图2 挡货立柱工况示意图（长度单位：mm）

1.3 受力分析

根据1.2节介绍可知，堆管横倾产生的作用力会作用在单侧的堆管立柱上，同时堆管自身会产生一个运动趋势反向摩擦力（见图3），由图3可知摩擦力对于堆场立柱是有利作用载荷，但设计阶段为挡货立柱安全使用考虑，取垫木µ的较小值0.4g作为计算用值。根据上述分析可将单侧立柱受力简化成图4超静定结构模型进行立柱载荷计算，计算公式见式（1）。

图3 堆场堆管受力示意图（长度单位：mm）

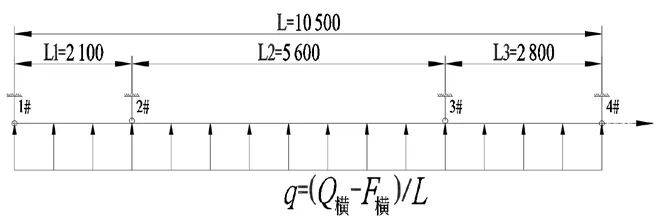
图4 单侧挡货立柱受力模型计算图（单位：mm）

式中：q为立柱载荷，N/mm；w为甲板均布承载能力，N/m2，由1.1节可知为0.01 N/m2；S为单跨堆管面积，mm2，本案例参考图3可知S=77.43×106mm2；L为简化模型总长度，mm，本案例参考图3为10 500 mm。得到计算结果为q=180.85 N/mm。

根据以上已知条件，可以看出该受力简化模型属于超静定结构，本案例重点在于求出各支撑点的支反力，而超静定的结构力学——力法、位移法等其他方法着重研究外载荷作用的弯矩[3-4]，故为了更有效准确地获得各支撑点支反力，综合考虑采用ANSYS的APDL配合BEAM3单元进行计算命令编写[5-6]，并通过“*ASK”命令将各立柱之间的间距L及均布载荷q设为可输入变量，以便于实际项目中堆场各跨设计及后期布置调整都可快速求得结果。

如图5所示，将上述荷载加载到ANSYS模型中，求得各支点垂直方向支反力，见表1。

图5 单侧挡货立柱ANSYS模型加载

表1 ANSYS APDL录入实际模型数据求解结果

根据表1可知，最大支反力发生在3#挡货立柱，其作用力为：Fy=0.76×106N。

2 挡货立柱详细设计

对于单根挡货立柱将1.3节求得的最大集中应力转换为沿挡货立柱垂向的均布载荷。另外，挡货立柱本身焊接于甲板为悬臂梁结构，故甲板根部不仅要承受最大集中应力，还要承受这对支返力的力偶作用。如图6所示，为减少焊缝受载，考虑增加抗剪块承受该水平应力，立柱与甲板间焊缝承受力偶，而立柱本体承受均布力作用的弯矩。

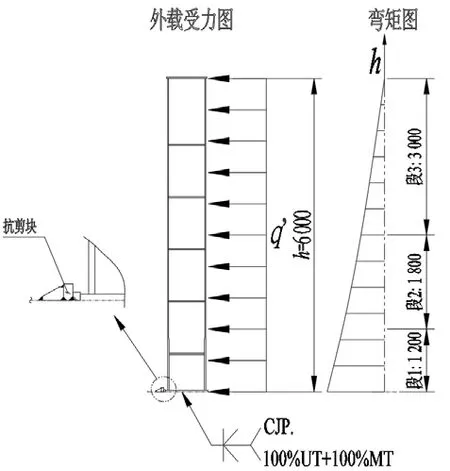
图6 单根挡货立柱受力分析图（单位：mm）

本文重点介绍铺管船挡货立柱布置、设计与强度计算。抗剪块与底板焊缝计算均属于焊缝强度计算，可参考钢结构焊接规范[7]。

根据力学分析，实际挡货立柱垂直方向上各点的弯矩Mh应为

式中：q'为最大支反力Fy在h长度上的等效作用，N/mm，q'=126.67 N/mm。

综合考虑实际项目生产成本，将立柱分为3段，通过不同的工字钢截面变化及各段最大弯矩来求解，得出各截面所需的抗弯截面系数，见表2。

根据表2信息，将挡货立柱方案进行细化，如图7所示。

图7 挡货立柱详细设计图（单位：mm）

表2 挡货立柱具体截面设计

3 基于有限元的受力分析

3.1 精细有限元模型

3.1.1 堆场挡货立柱有限元模型

根据表2的计算结果和图7设计详图制作挡货立柱实体模型，并通过实际加载论证上述设计方法的可靠性，见图8。根据图2可知挡货立柱的布置范围在跨距12 m、宽度8 m的范围内。为使结构计算更贴合实际，反面加强及甲板建模选用跨距14.7 m、宽度12.6 m的扩大范围进行建模[8]。

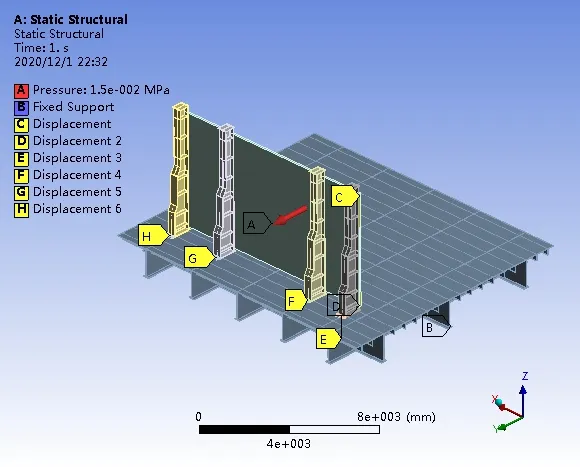
图8 挡货立柱设计方案

本文挡货立柱受载屈服准则需满足表3要求，且所得各立柱支反力数据与APDL计算结果偏差应控制在10%以内。

表3 项目规定有限元计算结果许用应力值

3.1.2有限元模型计算工况

根据3.1.1的模型概述及第2节所介绍的约束条件进行挡货立柱ANSYS建模及约束施加。而外部载荷则以建立该区域挡货立柱受载刚性体作为均布载荷以贴近真实工况表现。该均布载荷值为

式中：S’为建立的受载刚性体表面积，mm2；经计算，q=0.015 N/mm2

3.2 有限元计算结果

3.2.1 立柱自身支反力

对比1.3节的ANSYS A PDL与3.1节ANSYS实体建模2种不同计算方法的各立柱支点的Fy值，并对计算结果进行偏差对比，得出表4。

表4 ANSYS APDL录入实际模型数据求解结果

3.2.2 立柱受载后各项应力

ANSYS实体建模计算后处理中，除获得支反力外，同时借助软件的应力后处理功能求得范式等效应力、剪切应力及正应力，结果见图9～图12。

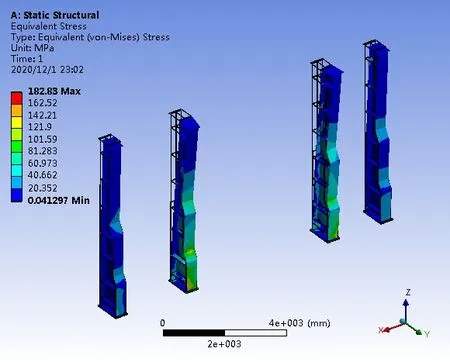
图9 范式等效应力结果

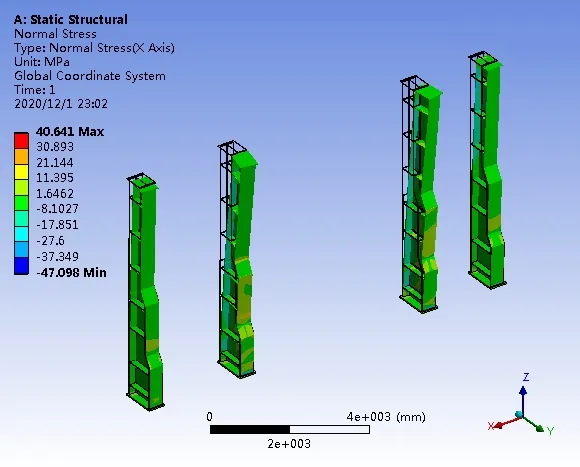
图10 正应力（X方向）结果

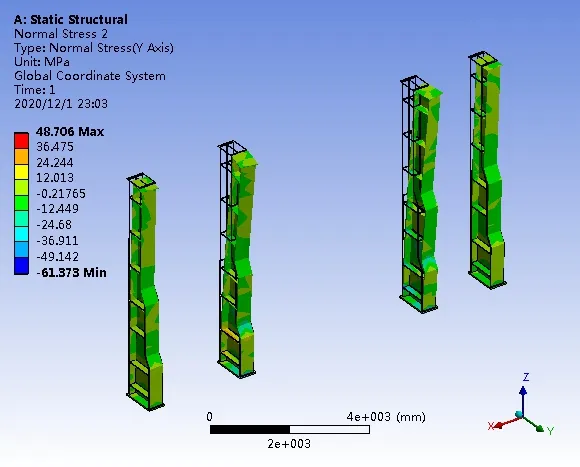
图11 正应力（Y方向）结果

图12 剪切应力结果

3.2.3 有限元计算结果以及支反力偏差对比

根据图7和图8实体建模后有限元分析结果，并与表3及APDL计算支反力进行对比，可得如表5所示的结果。

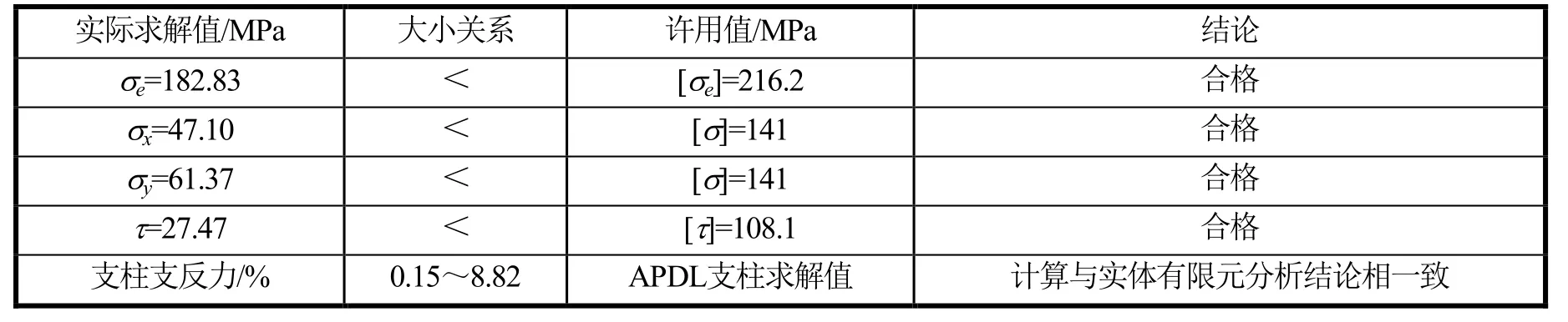
表5 各项指标评判结果

4 结论

本文首先进行铺管船堆场挡货立柱的布置及载荷模型简化，再根据其超静定的布置特性编写ANSYS APDL载荷计算命令获取立柱支反力。通过将所求得的最大支反力转换为均布载荷以确定挡货立柱的有效变截面设计方案。在此基础上，通过实体建模加有限元分析佐证该设计方法。最后对计算结果进行对比，得到如下结论：

1）本文所提供铺管船堆场挡货立柱的设计方法具有足够的精度可供工程设计参考。

2）本文通过某多功能铺管船堆场挡货立柱的布置、载荷求解、立柱设计为例，给出图10铺管船堆场挡货立柱的设计方案，并筛选出设计中的可变参数，便于不同项目间的方法通用性或项目实施过程中布置的调整，可以快速求解给予响应。