强风化花岗岩隧道二次衬砌支护时机研究

杨平 张成良 邱坚 叶丹勇 赵任旭 李鹏

(1.昆明理工大学公共安全与应急管理学院 昆明 650093； 2.昆明理工大学国土资源工程学院 昆明 650093； 3.云南升盟工程咨询有限公司 昆明 650217)

0 引言

在实际工程施工中针对不同的地质围岩条件和施工方法，合适的支护时机非常重要。恰当的支护时机，可以让围岩与支护体系形成一个承载共同体，使衬砌承受最好的力。PANET M[1]提出了收敛极限法，通过反演分析拱顶沉降及水平收敛位移值，确定应力释放率，从而选择支护时机；杨红军等[2]进行了半解析计算分析，针对不同围岩等级分别给出了相应支护时机；王中文等[3]将公式与数据相结合，求出拟合方程从而得出围岩变形规律。声发射在测定围岩稳定性中逐渐广泛应用起来，是用来探究岩石损伤演化机理的一种关键手段[4]，RUDAJEV V等[5]通过压缩试验分析总结出岩石试件AE参数的分布规律与破坏过程之间的联系；张艳博等[6]通过对自然花岗岩做单轴压缩实验，总结了花岗岩破裂过程声发射变化规律特征；赵康等[7]运用RFPA 2D软件，对各种岩石在施加点荷载时声发射时频特征、尺寸效应关系做了研究。声发射评价岩体内部活跃情况从而分析其稳定性在矿山中得到广泛应用，在隧道围岩稳定性分析中也开始应用起来[8]。受材料非均质性的影响，岩石的尺寸效应的研究，在工程中逐渐得到重视。

许多学者都是利用围岩位移或应力释放来选择支护时机的，但忽略了岩体内部破坏损伤机理，往往具有局限性，因此仅利用围岩位移和应力释放来判断岩体稳定性是单一的、不全面的，需要结合围岩内声发射能量和个数的变化，综合评判围岩稳定性，从而选择更合适的支护时机。

本文应用RFPA软件考虑尺寸效应，研究不同试件及隧道模型，在位移加载下的变形破坏和应力变化规律及声发射能量信息，分析总结得出规律，并通过隧道现场声发射、应力位移监测信息比较，综合判定强风化花岗岩的二衬支护时机，并在施工现场进行验证，为实际工程施工提供指导意义。

1 工程地质概况

梁河隧道属于浅埋隧道，隧址位于腾冲—梁河弧形构造带与槟榔江弧形构造带复合部位，地形地貌及地层分布主要受大盈江断裂控制。大盈江断裂形成于古生界，至新构造期又复活，在第四系时活动强烈，并引发多次地震。其次级断裂控制了侵入岩、变质岩的分布，使局部地段岩性变化大，工程地质条件差异明显。总体上，隧址区区域断裂发育，地质条件复杂，在区域断裂破碎带的影响下，隧道围岩以V级全～强风化黑云母花岗岩为主，胶结程度差，岩体裂隙发育，在主要节理裂隙及次生风化裂隙的共同切割作用下多呈碎块状、块状结构，局部位置呈碎裂状、镶嵌碎裂状结构岩体。

2 数值模拟与分析

为确定强风化花岗岩的支护时机，需要掌握岩体的应力、应变过程及其破坏特征，采用RFPA软件建模分析，建立不同尺寸的岩样、岩体和隧道模型，考虑尺寸效应对岩样强度和应力的影响，寻求不同尺寸条件下试样应力、声发射变化规律及差异性，从而使分析更准确，并结合现场监测信息综合确定出二衬支护的时机。

2.1 岩样尺寸数值分析

本实验取H/D=2的圆柱体岩样模型，模型尺寸分别为50 mm×100 mm、75 mm×150 mm、100 mm×200 mm、150 mm×300 mm、200 mm×400 mm，每组实验参数依照强风化花岗岩室内实验得出的岩石力学参数为依据，内摩擦角为35.5°，压拉比为10，拉变系数取1.5，泊松比μ为0.25，均质度取3，细观平均值取70，强度折减系数取0.01，采用单轴压缩方式，每步加载位移量△S=0.002 mm，单元网格数为100×200，其单元体泊松比及弹性模量等力学参数服从Weibull函数分布，采用摩尔-库伦破坏准则，分析模型破坏过程。

2.1.1 不同岩样尺寸应力-应变分析

岩样应力-应变关系见图1、岩样峰值应力-尺寸变化关系见图2。

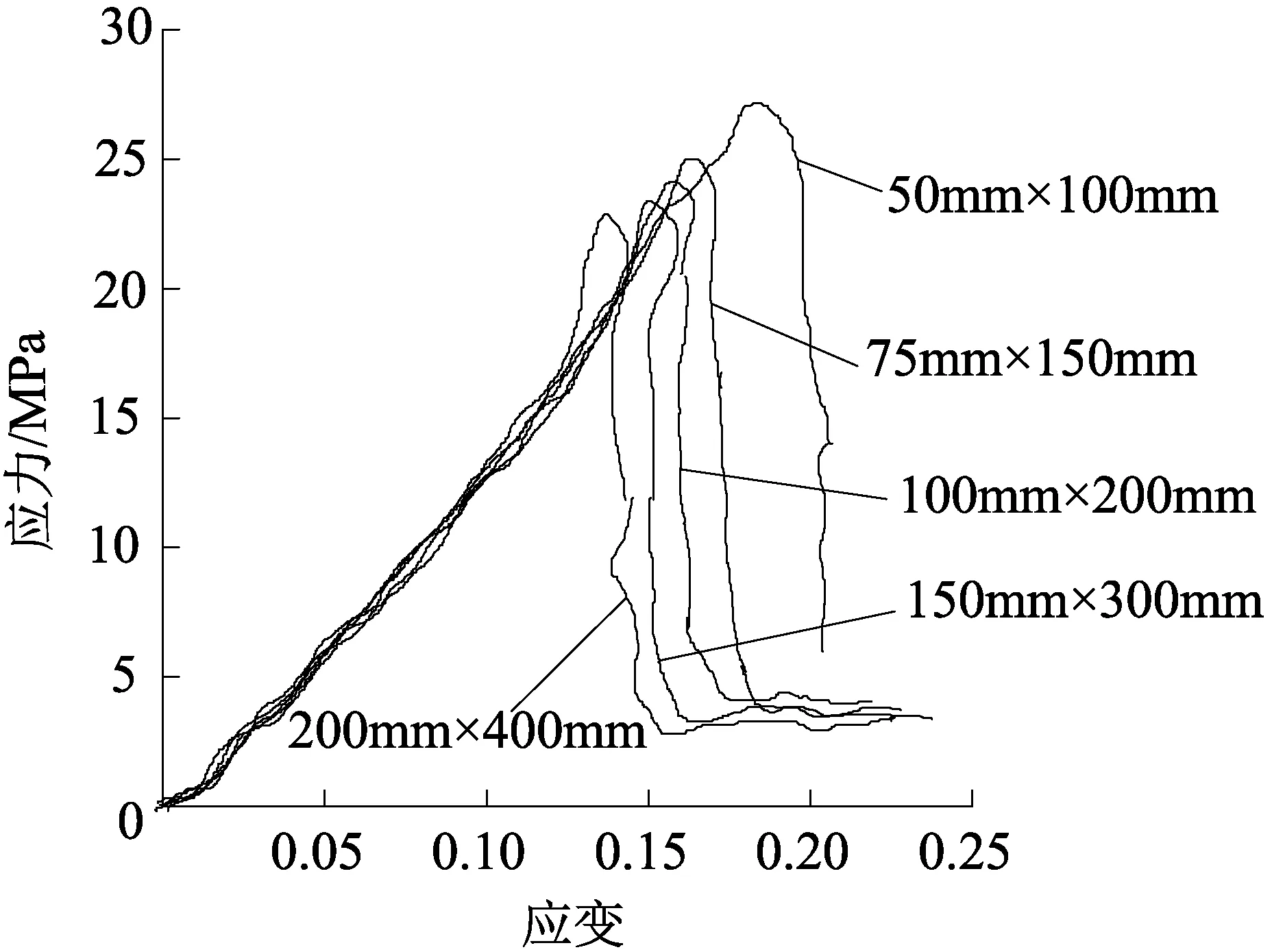
图1 岩样应力-应变关系曲线

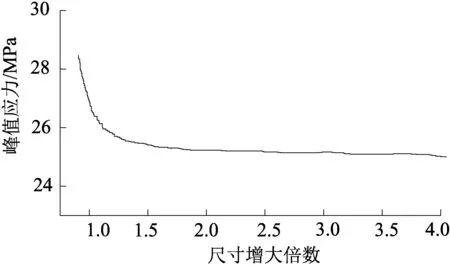
图2 岩样峰值应力-尺寸变化关系曲线

由图1可知弹性模量随岩石尺寸的增大而减小，岩样中微裂隙就会增多，从而导致岩石的弹性模量减小，细观缺陷的增多导致非均质性增大是尺寸效应的重要原因，峰值强度随岩石尺寸的增大而减小，岩石破坏由塑性破坏转变为脆性破坏。由图2可知随着尺寸增大,多组试件的强度越来越趋向于稳定，而大于这一尺寸范围时,其强度基本保持一个较为稳定的值。

2.1.2 不同岩样尺寸破坏及声发射分析

不同岩样尺寸破坏及声发射分别见图3、图4。

50 mm×100 mm 75 mm×150 mm 100 mm×200 mm 150 mm×300 mm 200 mm×400 mm

50 mm×100 mm 75 mm×150 mm 100 mm×200 mm 150 mm×300 mm 200 mm×400 mm

由图3可知在单轴加载过程中，当岩样的高度变大时，其中部的应力区就越接近于一维应力状态，破坏基本上开始沿左下角区域开始剪切破坏；当岩样高度变小时，其整体都会受到三维应力区的约束，破坏形式就更为复杂，在岩石的破坏形式上，为裂纹破坏和剪切破坏。

图4中圆圈所处的位置代表声发射的位置，光圈的大小表示声发射能量的相对大小，深色光圈代表拉破坏，白色光圈表示剪破坏。随着加载步的进行，岩石内部颗粒之间的摩擦或裂纹的张开，声发射不断增加，对比岩石破裂位置可知，声发射数同岩石的裂纹扩展部位相一致。由图4可知150 mm×300 mm和200 mm×400 mm岩样破裂单元最少，75 mm×150 mm次之，50 mm×100 mm最多，说明声发射活跃性随岩石高度增大而降低，小岩样试件声发射能量大于大岩样试件声发射能量，可以看出大试件岩样内部晶粒多，储存弹性势能多，更能抵抗破坏。其中50 mm×100 mm和100 mm×200 mm试件深色光圈较多，以拉破坏为主，150 mm×300 mm和200 mm×400 mm白色光圈多，以剪切破坏为主，小试件深色光圈较多，以拉破坏为主；从试件破坏图可以看出，小试件以横向裂隙和局部剪切破坏为主，大试件以剪切为主。

2.1.3 不同岩样尺寸损伤-应变分析

岩样损伤-应变曲线见图5。

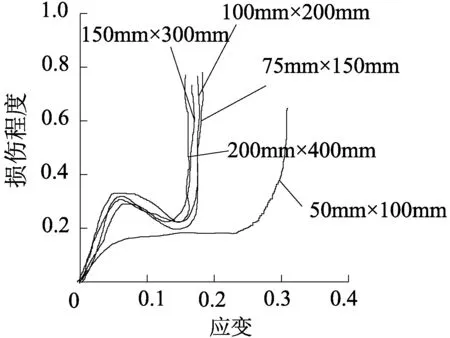
图5 岩样损伤-应变曲线

由图5可知损伤-应变曲线大概分为4个阶段：最初等速增加阶段、缓慢增长阶段、减少阶段和急速增长阶段，所有试件在最初塑性应变阶段，损伤在这区域内是急剧增加的，随着应变的增加在接近峰值时，岩体的损伤增加速率随应变的增加而不断减小，高度较小的试件，塑性更大，尺寸大的试件在彻底破裂时，相应的应变比小试件小，表明大试件塑性阶段相对较短，脆性破坏更为明显。由图可以看出随着试件尺寸的增大，当应变达到0.12范围内时，发生脆性破坏，衬砌支护的施作应在塑性阶段。

2.2 岩体尺寸模型设计与结果分析

实验选取的力学参数与岩样模型相同，取5组岩体试样模型，尺寸分别为3 m×6 m，6 m×12 m，9 m×18 m，12 m×24 m，15 m×30 m，采用竖向位移加载，△S=0.003 mm，单元网格数都为100×200，其单元体的泊松比及弹性模量等力学参数服从Weibull函数分布，采用摩尔-库伦破坏准则为依据，分析模型破坏过程。

2.2.1 不同岩体尺寸应力-应变分析

岩体应力-应变关系见图6，岩体峰值应力-尺寸变化关系见图7。

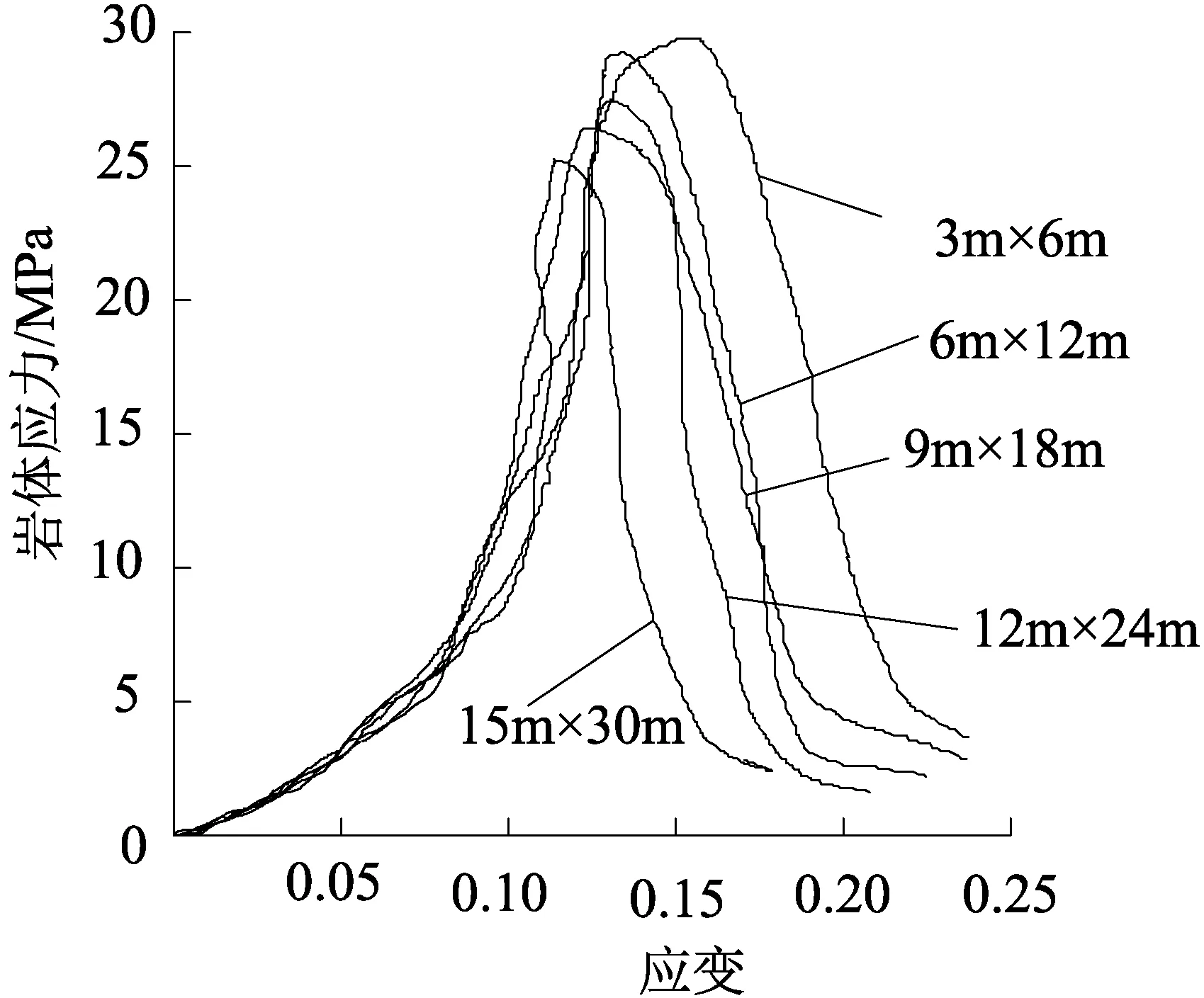
图6 岩体应力-应变关系曲线

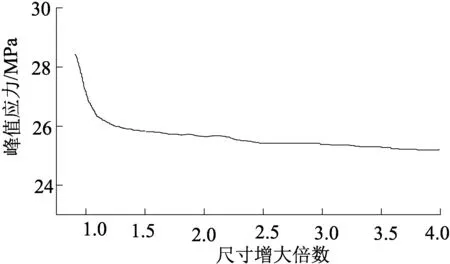
图7 岩体峰值应力-尺寸变化关系曲线

随着尺寸增大,其内部缺陷增多，岩体的尺寸效应明显突出。从图6和图7可以看出岩体应力-应变关系曲线可知，破坏前斜率随着岩石试样高度减小而减小，弹性模量逐渐变小，且峰值强度也略有下降，对比图1岩样应力-应变曲线可知，峰后阶段，曲线相对光滑均匀，体现出岩体的脆性破坏更突出。

2.2.2 不同岩体尺寸破坏及声发射分析

不同岩体尺寸破坏及声发射情况见图8、图9。

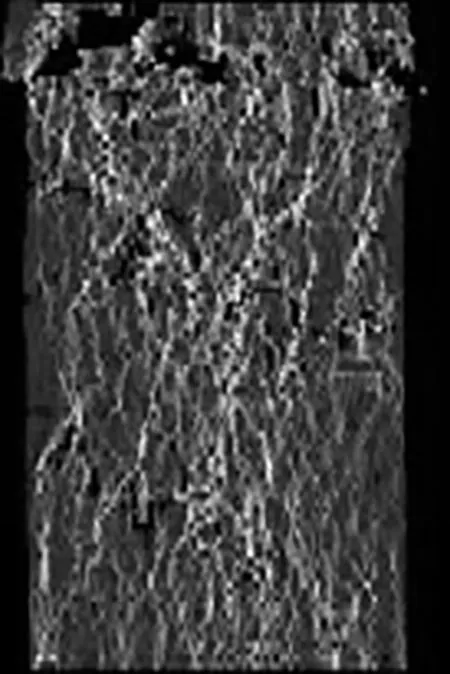
3 m×6 m 6 m×12 m 9 m×18 m 12 m×24 m 15 m×30 m

由图8可以看出小试件多出现裂纹，且分布较散，为多裂隙拉伸破坏，由于泊松效应的存在，随试件高度的增加，模型形成以中间区域为主裂纹的偏轴向劈裂和剪切破坏。

3 m×6 m 6 m×12 m 9 m×18 m 12 m×24 m 15 m×30 m

如图9所示，声发射圈出现的位置与岩体破裂位置大致重合，由光圈颜色可知，小岩体白色光圈为主，大岩体深色光圈为主，随着岩体尺寸增大由拉破坏逐步过渡到剪破坏，相比岩样试件的声发射破坏能量而言，岩体的圆圈增多，能量也变大，说明了岩体的破坏损伤更大，对比岩样试件声发射破坏图，在相同加载步下，岩体的声发射破坏信息提前与岩样试件，说明随着试件尺寸增大，破坏损伤就越提前。

2.2.3 不同岩样尺寸损伤-应变分析

岩体损伤-应变曲线见图10。

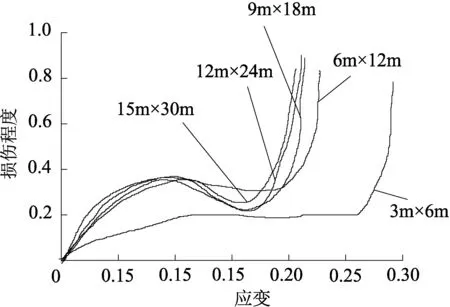
图10 岩体损伤-应变曲线

由图10曲线可知岩体试件高度越小，在最初所发生的损伤曲线就越平缓，波动性较小，说明其塑性越大。在峰值强度之前不同高度的岩石试件所达到的损伤值相差不大。在达到峰值强度时岩石试件的损伤会剧增，但高度的岩石试件损伤增加会稍微缓慢，随着尺寸的增加，当应变在0.13左右时，大试件发生脆性破坏，结合应力-应变曲线可知，衬砌的施作应在脆性破坏前。

2.3 隧道模型设计与结果分析

由于隧道的围岩压力主要为松动压力和形变压力，应用RFPA软件模拟隧道开挖立即施作初期支护后，从不同台阶开挖到仰拱施作完成期间围岩应力、声发射随台阶开挖施工的影响变化规律，并考虑边界效应影响，隧道模型左右边界距离不少于2.5倍隧道半径，隧道跨度11.8 m，隧道仰拱距离边界底部不少于3倍隧道高度。隧道模型如图11所示，隧道应力见图12。

现场对进口右幅YK37+048—YK37+055段和YK37+075—YK37+082段及出口右幅YK37+405—YK37+412段3段浅埋围岩在台阶开挖下应力及破坏进行研究，3段围岩级别均为V级，各段埋深分别为32 m、33 m、36 m，各段的围岩参数如表1所示。

剪应力 最大主应力

表1 各段围岩参数

由图12中剪应力图和最大主应力图可知，拱顶和仰拱先后出现了断裂，说明在隧道开挖卸荷后，应及时施作初期支护，从应力变化图可以看出在拱肩和拱腰这两个部位产生了应力集中的现象，隧道拱肩部位的应力会跟着上台阶开挖卸荷的影响不断向拱腰偏移，在拱腰部位出现明显的应力集中效应，所以拱腰处的应力大于拱顶和拱肩，最后中、下台阶开挖及仰拱施作，边墙处的塑性区范围逐渐增大并与拱脚处塑性区产生贯通连接。

3 现场应力、声发射监测

隧道的施工方法为三台阶七步开挖法，现场采用应力计和声发射检测计对开挖后立即施作初支后的掌子面，在不同台阶开挖步骤施工过程中围岩的应力和声发射进行监测，分析开挖过程中拱顶、拱腰的应力释放与声发射变化规律，并与模拟分析对比，确切提出二衬支护时机。

3.1 隧道围岩应力监测

围岩应力监测曲线见图13。

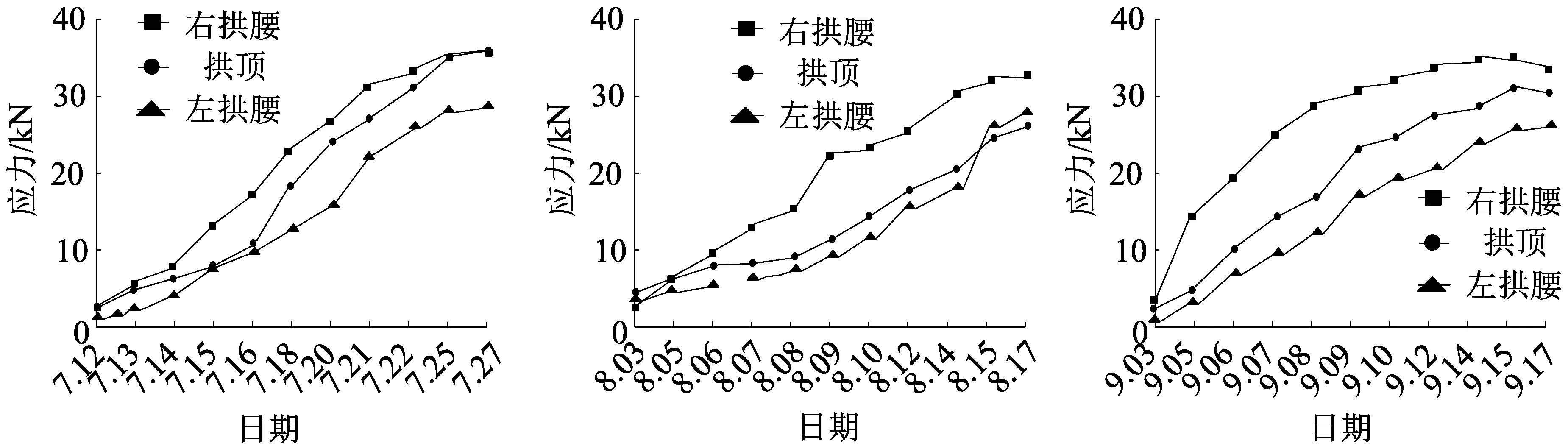
(a)YK37+050段 (b)YK37+075段 (c)YK37+125段

三段围岩分别位于进口右幅和出口右幅，最大应力小于32 kN，且应力大小为右拱腰>拱顶>左拱腰，与RFPA数值模拟一致，说明了RFPA模拟的可靠性。进口段围岩稳定性和完整性相对要差，承受的应力更大，主要原因是受压扭性构造作用，岩体赋存了一定的水平地应力，监测结果和规律呈现出一定的方向性。如图13应力监测显示各围岩段第1～6 d处于上台阶开挖阶段，由于开挖卸荷作用，各部位应力增长过快，7～12 d受中、下台阶开挖并进行仰拱施工影响，应力逐渐移动，拱腰处出现应力集中现象，隧道开挖约16 d后，应力保持基本稳定，变化速率近乎为零，由此可以推断二衬施作时机约为15 d。

3.2 隧道断面声发射

能量-时间联合图见图14。

由图14可知声发射表现是1～6 d内随上台阶开挖后能量大、事件多、岩体应力扰动和调整频繁，7～14 d期间随着中、下台阶开挖及仰拱成环后，能量减小、大事件变少，表现为岩体处于比较稳定状态，因此可知二衬施作时机约为15 d左右。

4 工程验证

各段二衬接触压力见图15。

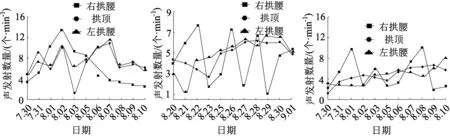
(a)YK37+050段 (b)YK37+075段 (c)YK37+125段

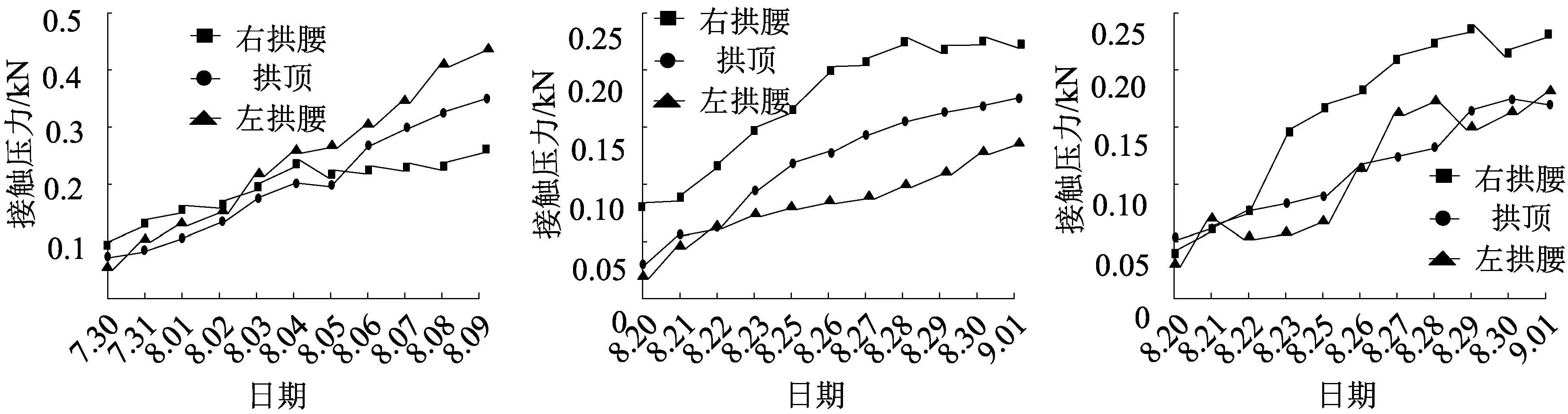
(a)YK37+050段 (b)YK37+075段 (c)YK37+125段

YK37+048—YK37+055段二衬在现场施工时间为2019年7月29日，约为初期支护后的16 d左右，图15(a)可以看出在二衬施作后，衬砌压力在前7d呈线性缓慢增长，之后趋于平稳；YK37+075—YK37+082段二衬的施作时间为8月19日，约为初期支护后的15 d左右。从图15(b)可以看出衬砌压力在前10天近似线性增长，且增长速率与图15(a)大概一致，之后进入平稳阶段；YK37+122—YK37+130段二衬施作时间为9月20日，约为初期之后的15 d左右。图15(c)可以看出二衬压力在前8天成线性增长，增长速率与图15(a)、图15(b)相比略有缓慢，之后便趋于稳定。现场调查以上3段隧道地段在二衬施作后均无裂缝、变形、鼓包等现象。综合以上数据分析及现场验证证明，初支完成大概15～16 d后，此时施做二衬支护是合理的。

5 结论

(1)由RFPA`软件模拟可以看出，试件尺寸越大，岩体破坏由塑性破坏趋向脆性破坏，声发射能量提前达到峰值。

(2)试件的峰值强度随尺寸的增大而减小，并逐渐趋于某一值。

(3)通过RFPA隧道模型数值模拟看出拱肩、拱腰部位出现应力集中现象，通过现场应力监测分析验证了RFPA的可靠性，再结合现声发射监测信息，综合判断得出支护时机。