远地点发动机推力矢量不确定度评估方法

郑 科 张 伟

(北京航天试验技术研究所，北京 100074)

1 引 言

远地点发动机常被用于星、箭、弹的精确轨道控制和姿态调整，其推力矢量直接关系到卫星能否入轨和发射任务的成败，准确测出推力矢量参数，能够为发动机整星组装时提供基本依据。目前，推力矢量测量有多种方案，在我国的远地点发动机高空模拟热标定试验中，技术和工艺都比较成熟且经多次飞行验证效果显著的是北京航天试验技术研究所1992年研制的动态轴矢量推力架和该所2010年研制的基于压电晶体测力板技术的多分力动态矢量推力架。

远地点发动机一般用于卫星等航天器的轨道控制和姿态调整。推力矢量测量的准确性对卫星能否入轨以及入轨成本有很大的影响，甚至影响卫星的工作寿命，所以推力矢量参数是发动机整星组装的重要参考依据。对于推力矢量的测量，在我国远地点发动机高空模拟热标定试验中，北京航天试验技术研究所1992年研制的动态轴矢量推力架和该所2010年研制的基于压电晶体测力板技术的多分力动态矢量推力架经过多次实际飞行验证，技术相对成熟。

2 动态轴矢量推力架测量模型

测试系统的推力矢量模型如图1所示，

O

-

XYZ

为转台坐标系，

O

’-

X

’

Y

’

Z

’为发动机坐标系，发动机热试车时产生的发动机推力矢量

F

作用于对接面

Y

’

O

’

Z

’平面的A点上。

图1 推力矢量模型

推力矢量

F

在推力轴线方向(

X

轴方向)的分量为

F

,其垂直于推力轴线方向的分量为

F

(

Z

’

O

’

Y

’平面内)，在转台上产生一个绕

Z

轴的旋转力矩

M

,经过简单力学推导可得-

M

=

F

(

δ

cos

β

+

R

tan

α

cos

γ

)

(1)

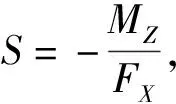
S

=

δ

cos

β

+

R

tan

α

cos

γ

(2)

当推力矢量装置使

Y

’

O

’

Z

’平面(即发动机对接面)绕

OX

轴旋转(角，公式(2)变为

S

=[

δ

cos(

β

+

θ

)+

R

tan

α

cos(

γ

+

θ

)]

(3)

其中

M

，

F

，

R

，

θ

为可测参数，

α

，

β

，

γ

，

δ

为待求参数。分别改变

R

和

θ

的值，令

i

=1,2,3,...,

n

,发动机点火

n

(

n

=6～8)次，求解方程组即可得到矢量参数

S

=[

δ

cos(

β

+

θ

)+

R

tan

α

cos(

γ

+

θ

)]=

δ

cos

β

cos

θ

-

δ

sin

β

sin

θ

+

R

tan

α

cos

γ

cos

θ

-

R

tan

α

sin

γ

sin

θ

(4)

令

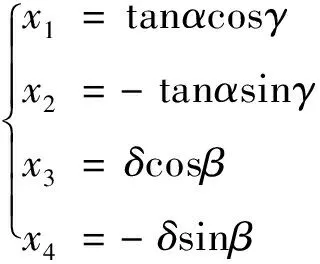
(5)

公式(4)可写为矩阵形式

在这里我们主要对帽壳进行研究分析后，决定采用如图2亚光表面处理，作为共享产品，使用时间长，接触人多，头盔表面难免留有很多划痕，而亚光表面的日常的划痕磨损会相对没有抛光表面易发现，所以，从造型美观来看，我们更倾向于使用亚光处理表面。同时亚光表面的处理，将会使头盔的造型感更加沉稳有质感。

AX

=

S

(6)

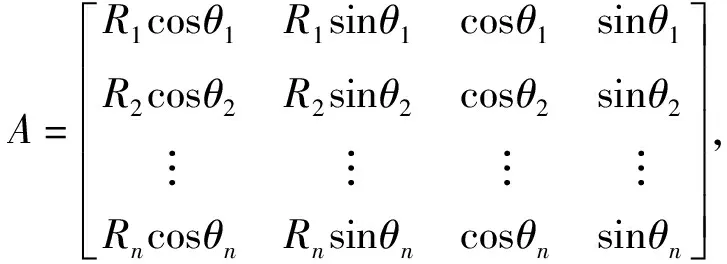
X

=[

x

x

x

x

]，

若

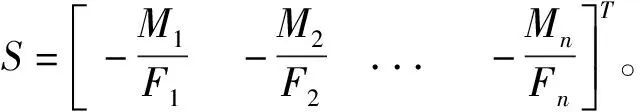
A

A

的逆矩阵(

A

A

)存在，则得到

X

的最小二乘解为

X

=(

A

A

)

A

S

(7)

推力矢量参数为

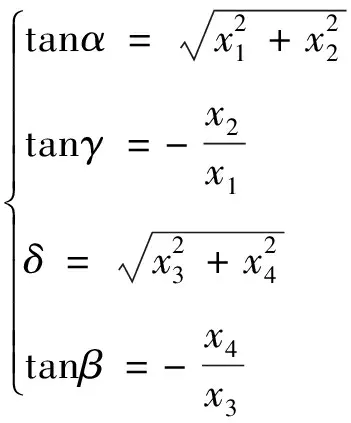
(8)

3 GUM不确定度评估

3.1 GUM法简介

GUM法通过测量模型直接传递不确定度，基于方和根法计算合成不确定度。方法源自《测量不确定度表示指南》，假设输出量近似为正态分布或者缩放位移t分布，通过设定包含概率、计算自由度以及查表求出对称的包含区间，也叫做不确定度传播率，尤其适合于测量模型为线性模型，是目前常用的测量不确定度评估方法。

3.2 GUM法评估过程

计算参数合成不确定度一般表达式为

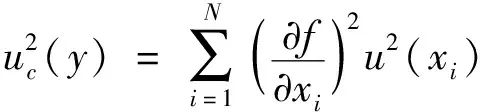
(9)

式中：

u

(

y

)——合成不确定度；

f

——被测量

y

与直接测得量

x

的函数关系；

u

(

x

)——分量

x

的不确定度。

根据公式(8)可以得到

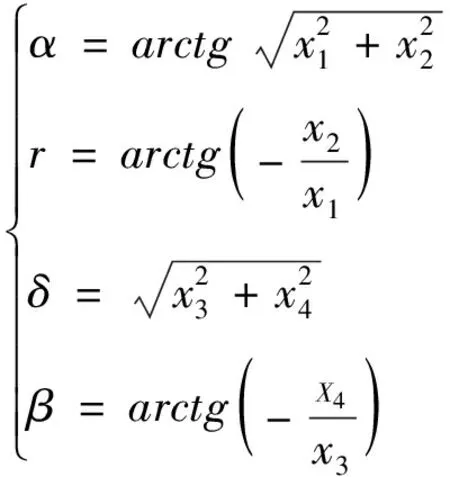
(10)

根据公式(9)计算得到各参数合成标准不确定度表达式为

(11)

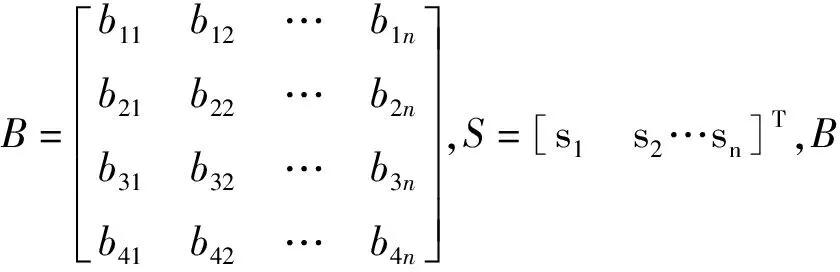
B

=(

A

A

)

A

(12)

公式(7)可以写为

X

=

BS

(13)

可得

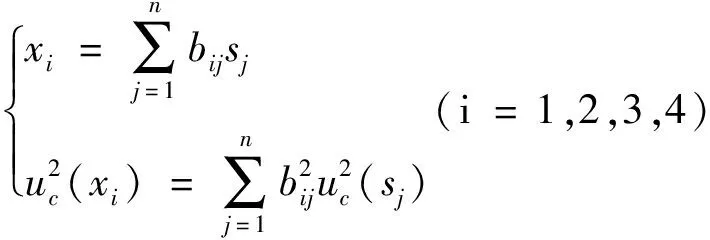
(14)

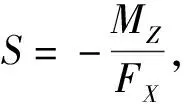
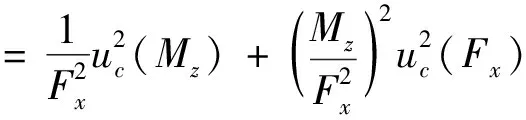
(15)

从表1中计算结果可以得出，

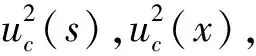
α

合成标准不确定度在0.005°以内；

β

合成标准不确定度基本在10°以内，

γ

合成标准不确定度在10°以内，

δ

合成标准不确定度在0.04mm以内。

3.3 GUM法在该模型评估中的局限性

计算合成标准不确定度的公式(9)忽略了泰勒级数的高价项以及相关性，当模型为复杂非线性模型时，近似为线性模型存在一定的误差。输出量的概率密度函数(Probability Density Function, PDF)偏离正态分布或缩放位移

t

分布时，概率分布偏离对称分布，采用GUM法得出的包含区间存在误差。由于

R

和

θ

的测量存在误差，导致

A

自身存在误差，由最小二乘法解出的矩阵

B

存在误差，最后通过GUM法得出的不确定度存在一定误差。

4 MCM不确定度评估方法

4.1 MCM原理

蒙特卡洛法为测量不确定度评估提供了一个通用的计算方式，适合多个输入量以及单个输出量的测量模型，输入量可以为任意的概率分布，相比GUM法，其对测量模型没有限制，省去了复杂灵敏度的计算。蒙特卡洛法的核心是对输入量的PDF重复采样，即利用对输入量概率分布的随机抽样代入测量模型进行分布传递，区别于GUM法的传递不确定度，其传递的是数值特性。计算出输出量Y的PDF离散采样值，由于离散采样值包含输出量Y的数值特性，因此可以从离散采样值中得到输出量的Y的最佳估计值和Y的标准不确定度，随着对概率密度函数的随机采样数M的增加，可提高不确定度、包含区间等数值特性的可靠性。蒙特卡洛法的概率分布传递原理图如图2所示。

表1 8台次热标矢量参数不确定度Tab.1 Uncertaintyofthrustvectorparametersineighttimes试车代号uc(α)/°uc(β)/°uc(γ)/°uc(δ)/mm10.00202.01.70.01820.00201.75.20.01930.00302.13.40.02540.00303.71.20.01850.00200.851.30.01660.00507.51.60.03370.00303.73.90.02980.00100.681.10.0060

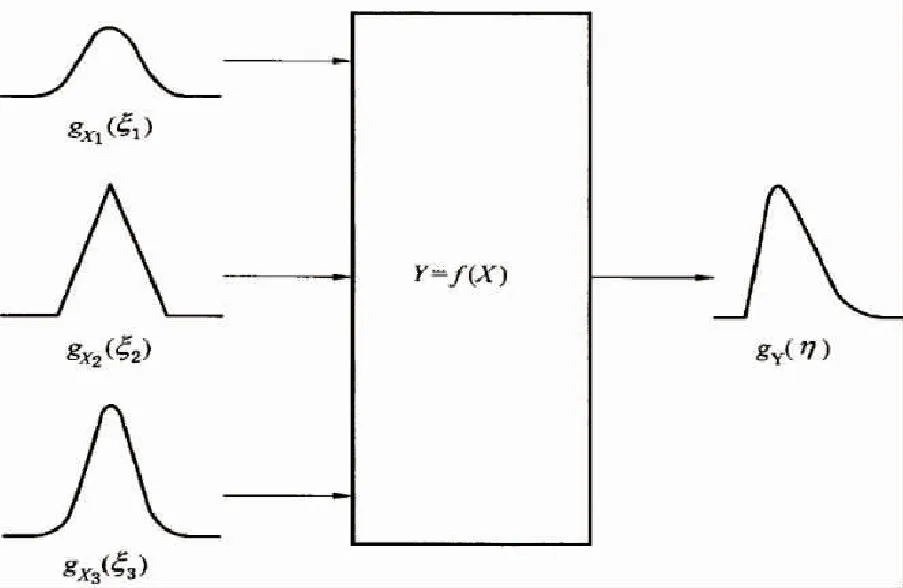
图2 由多输入量PDF得到单一输出量PDF的示意图

4.2 MCM评估过程

(1)定义输出量

Y

，即推力矢量参数(

δ

,

α

,

β

,

γ

)。(2)确定与

Y

相关的输入量

X

(

F

)、

X

(

M

)、

X

(

R

)、

X

(

θ

)。(3)建立

Y

和

X

之间的模型

Y

=f(

X

,

X

,

X

,

X

)。(4)利用可获信息，为

X

设定PDF，如正态分布、均匀分布等。对于

X

和

X

可以采用反复动作调整推力架50次，再直接测量长度(

X

)和角度(

X

)各50次的方法，分别确定

X

和

X

的PDF。对于

X

(

F

)和

X

(

M

)，在确定

X

和

X

的某一特定状态下，采用现场反复施加静态力的方法，获取

X

和

X

的分布样本各50次，再根据样本的概率统计评估其PDF。(5)根据蒙特卡洛法的相关国家标准，试验样本量的大小

M

，本次初步选取经验值10个。(6)从输入量

X

的PDF中随机抽取

M

个样本(

X

,

X

,

X

,

X

)，

r

=1,2,...,

M

。(7)对每个样本向量(

X

,

X

,

X

,

X

)，计算相应

Y

的模型值y=f[(

x

,

x

,

x

,

x

)]。

(8)将计算得到的M个模型值按照递增顺序排序，得出输出量Y的离散表示G。

(9)由输出量的离散表示G计算Y的期望值以及标准差，求出估计值y和不确定度μ(y)。

(10)通过输出量的离散表示G求出设定包含概率下的包含区间。

4.3 MCM的MATLAB实现及结果比较

极限情况下，

α

=0时，

γ

计算结果失真；

δ

=0时，

β

计算结果失真。按照机械加工的计量精测和往次试验结果统计，实际

α

值大多分布在(0.02～0.2)°以内，合格验收标准为

α

≤0.2°；

δ

值大多分布在(0.06～0.95)mm以内，合格验收标准为

δ

≤0.9mm；

β

和

γ

作为

δ

和

α

的定位角，存在批次性在类似象限的散布问题。根据推力矢量计算的数学模型，给定一组真值：

F

=489；(

δ

,

α

,

β

,

γ

)=(0.08,0.05,16,200)；对应

R

=[418

.

9 418

.

9 418

.

9 418

.

9 496

.

72 496

.

72 496

.

72 496

.

72]，

θ

=[0 30 60 90 90 60 30 0]。计算得到

M

=[130

.

37 87

.

73 21

.

58-50

.

36-61

.

71 27

.

34 109

.

07 161

.

58]。通过MATLAB编写软件，固化GUM法流程，导入数据，不确定计算结果为：

u

(

δ

)=0.0115mm，

u

(

α

)=0.0014°，

u

(

β

)=4.9699°，

u

(

γ

)=1.0514°，如图3所示。依据概率统计相关理论，扩展因子

k

=2时，

p

=0.95；

k

=3时，

p

=0.99。故可将当前的不确定评估结果根据需要，加权扩展因子

k

。

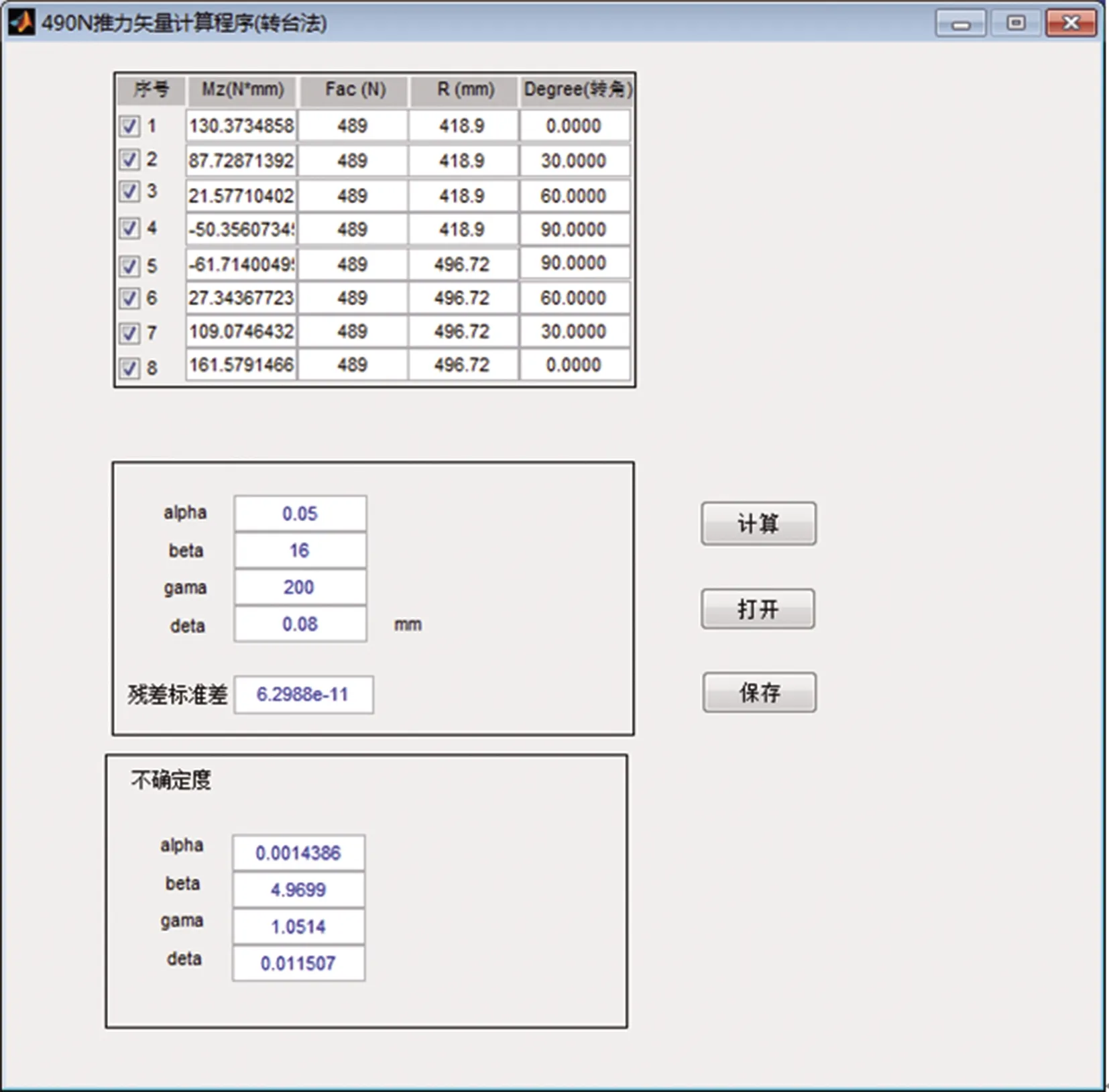
图3 GUM法计算程序

依据

F

、

M

、

R

、

θ

各自的PDF(

F

±0.5%随机发散、

M

±1%随机发散、

R

±0.05%随机发散、

θ

±0.05%随机发散)，进行MCM不确定度评估。通过MATLAB实现MCM的软件实现，采用4.2节的评估过程，如图4所示，针对该真值的不确定度评估结果为：

u

(

δ

)=0.0103mm，

u

(

α

)=0.0013°，

u

(

β

)=2.7089°，

u

(

γ

)=0.5135°，10个样本散布如图5所示(横坐标为数值，纵坐标为出现次数)。相比GUM法不确定度评估，MCM可以计算任何概率下的包含区间。MCM与GUM法结果对比如表2。

图4 MCM计算程序

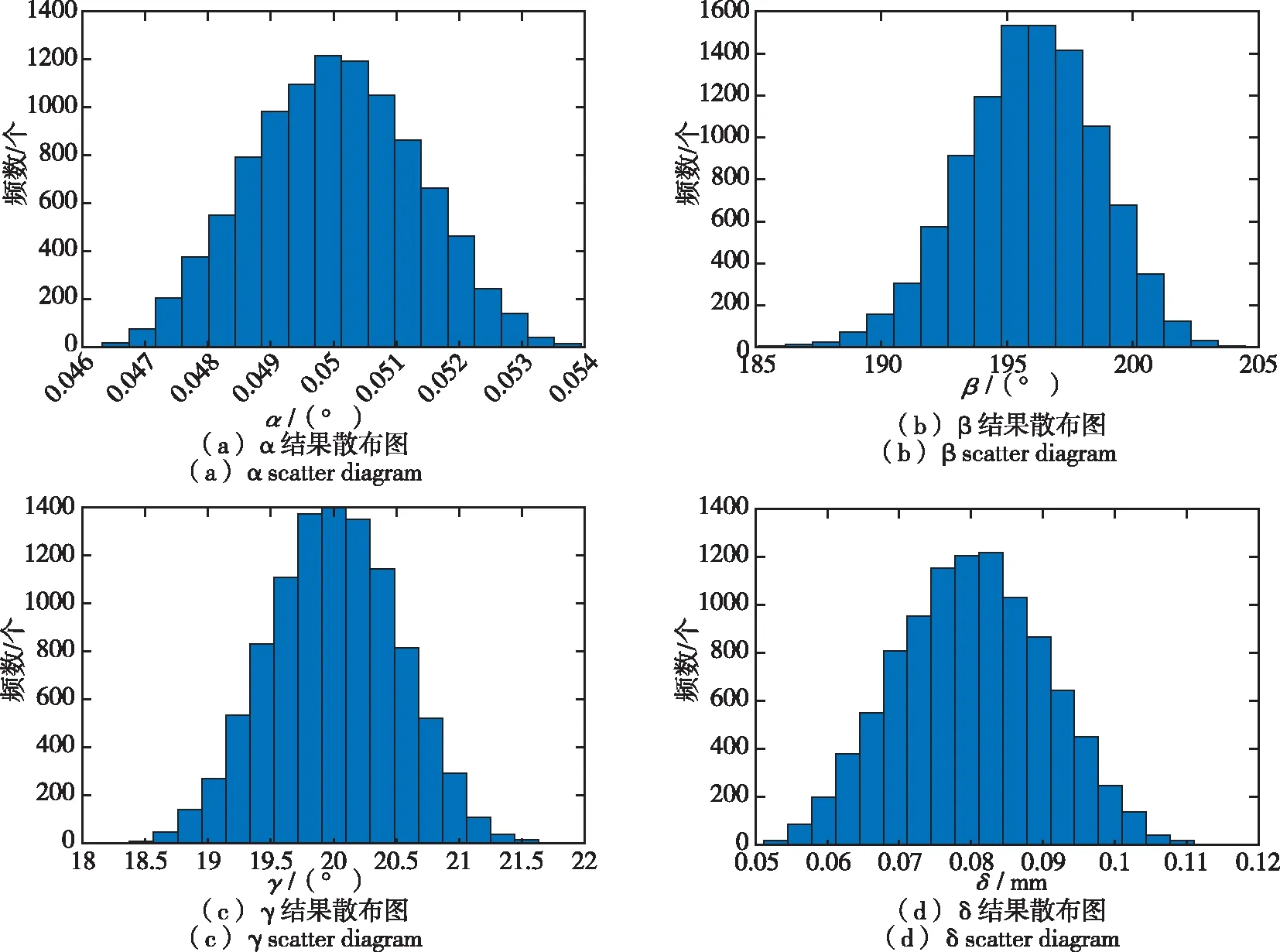
图5 结果散布图

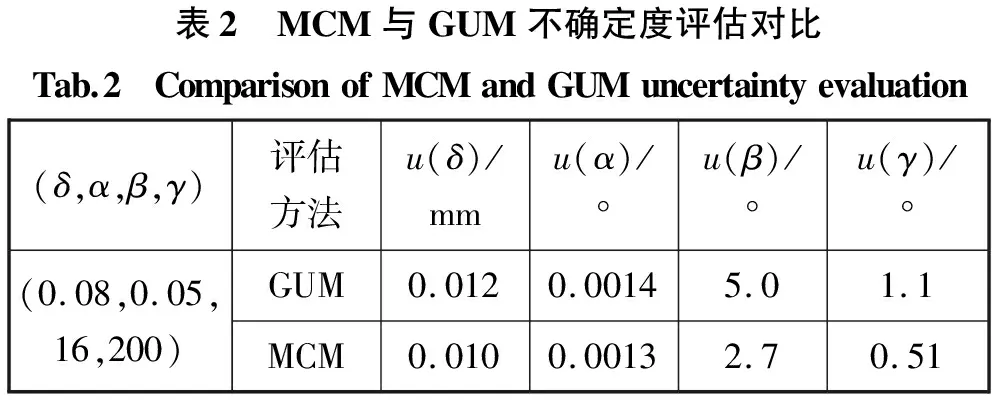
表2 MCM与GUM不确定度评估对比Tab.2 ComparisonofMCMandGUMuncertaintyevaluation(δ,α,β,γ)评估方法u(δ)/mmu(α)/°u(β)/°u(γ)/°(0.08,0.05,16,200)GUM0.0120.00145.01.1MCM0.0100.00132.70.51

4.3.1 其他数据的对比验证

不改变

F

，

R

，

θ

，改变(

δ

,

α

,

β

,

γ

)进行验证，初始值

F

=489，

R

=[418

.

9 418

.

9 418

.

9 418

.

9 496

.

72 496

.

72 496

.

72 496

.

72]，

θ

=[0 30 60 90 90 60 30 0]，计算

M

，结果如表3，不确定度的评估对比如表4。

通过数据对比得出，MCM评估的不确定度数值基本小于GUM法计算的不确定度数值，GUM法相对保守。

5 GUM法与MCM的区别和联系

从该远地点发动机推力矢量不确定度评估计算过程来看，GUM法是对多个输入变量的某一种特定组合进行计算，得到一个输出结果；而MCM在各个输入变量PDF的约束下，随机进行多个输入变量的

M

次采样组合，计算得出

M

个输出结果，再将

M

个输出结果作为统计样本，计算样本的期望和方差，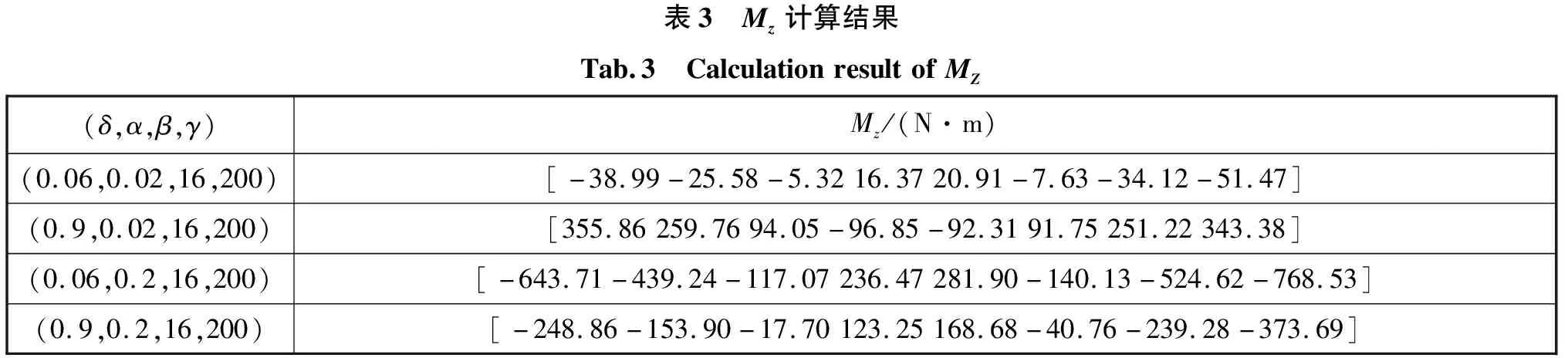

表3 Mz计算结果Tab.3 CalculationresultofMZ(δ,α,β,γ)Mz/(N·m)(0.06,0.02,16,200)[-38.99-25.58-5.3216.3720.91-7.63-34.12-51.47](0.9,0.02,16,200)[355.86259.7694.05-96.85-92.3191.75251.22343.38](0.06,0.2,16,200)[-643.71-439.24-117.07236.47281.90-140.13-524.62-768.53](0.9,0.2,16,200)[-248.86-153.90-17.70123.25168.68-40.76-239.28-373.69]

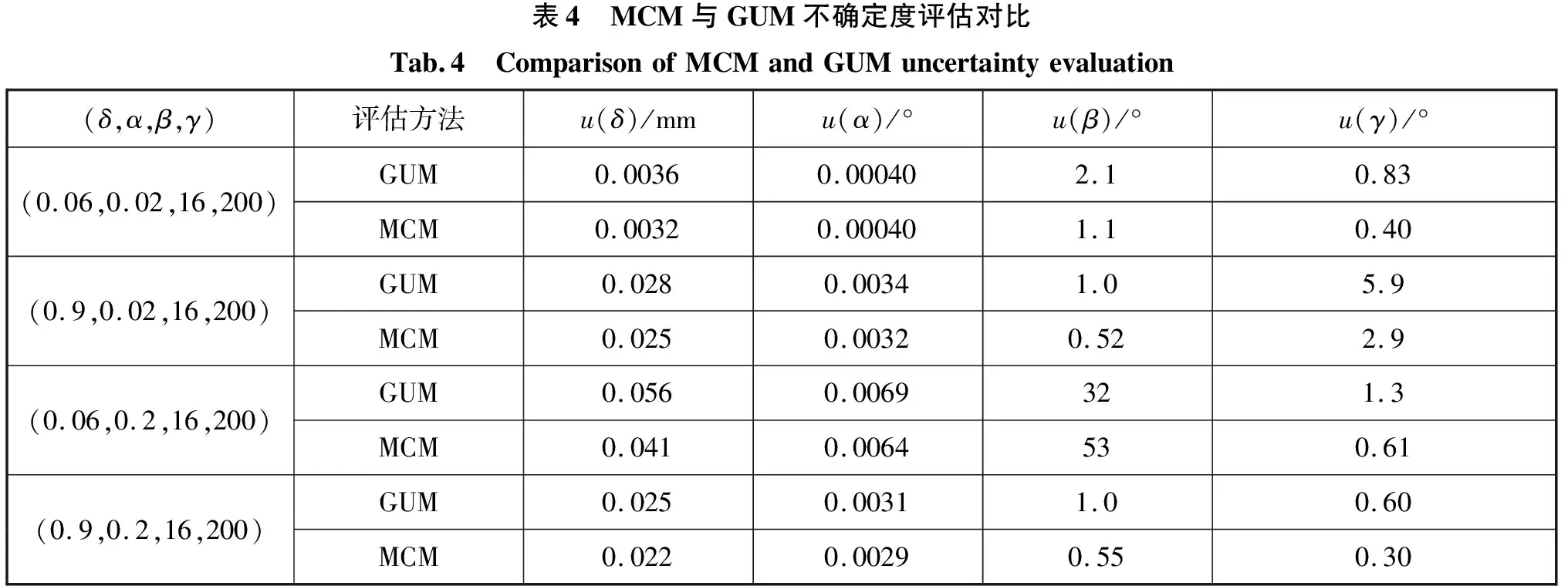
表4 MCM与GUM不确定度评估对比Tab.4 ComparisonofMCMandGUMuncertaintyevaluation(δ,α,β,γ)评估方法u(δ)/mmu(α)/°u(β)/°u(γ)/°(0.06,0.02,16,200)GUM0.00360.000402.10.83MCM0.00320.000401.10.40(0.9,0.02,16,200)GUM0.0280.00341.05.9MCM0.0250.00320.522.9(0.06,0.2,16,200)GUM0.0560.0069321.3MCM0.0410.0064530.61(0.9,0.2,16,200)GUM0.0250.00311.00.60MCM0.0220.00290.550.30