土质心墙堆石坝非饱和渗流参数反演

尹 川，吴震宇，王 媛，卞 康

(1.四川大学水力学与山区河流开发保护国家重点实验室 水利水电学院，四川 成都 610065；2.成都市市政工程设计研究院有限公司，四川 成都 610000)

因具备对地形地质条件适应性好，抗震性能优良，能就地取材和充分利用建筑物开挖料等特点，土质心墙堆石坝成为我国西部高坝广泛采用的坝型之一，如瀑布沟(186m)、长河坝(240m)、双江口(312m)等。土质防渗体的工作性态是心墙堆石坝长期运行安全监控的关键项目之一。水库水位变化范围内的心墙渗流性态与防渗土料的非饱和渗流特性密切相关，在水库水位快速变化条件下，土质心墙可能发生渗透破坏。

对于防渗土料的非饱和渗流特性，众多学者开展了相关研究。Rahardjo[1]通过非饱和数值模拟对比现场吸力，发现边界条件对土体吸力的影响。Khanh[2]通过分析瞬态非饱和渗流条件下的边坡稳定性，研究降雨诱发边坡破坏的潜在机制。胡云进[3]建立了单裂隙非饱和渗流模型，研究了渗透系数以及初始饱和度对裂隙渗透性的影响。数值模拟是预测心墙堆石坝渗流性态的有力工具，但其预测精度主要取决于合理的渗流材料模型及参数。基于原观数据进行模型识别和参数反演，以提高渗流数值模拟精度是目前工程中常用的方法。Strauss[4]基于贝叶斯理论进行渗透率统计反演，解决多孔介质中单相渗流的渗透率病态问题。岑建[5]以中线式尾矿坝为例，改进加速遗传算法反演岩土渗透系数，为分析该工程运行到最终坝顶标高时的渗流场提供依据。石春池针对糯扎渡高心墙堆石坝，利用粒子群优化算法优化径向基函数神经网络，基于实测渗压反演坝体的渗透系数，并利用非饱和非稳定渗流场测试反演结果。

近年来，为了使得反演结果更加真实地反映材料的实际渗流参数，人们不断地引入优化算法，进行各分区渗透系数的反演分析，应用于工程实践，且都取得了丰硕的成果。然而他们大多将渗透系数视为常数，认为材料的渗透特性不会随环境量的波动而改变。实际上，饱和土的渗透系数的确可以认为是常量，但非饱和土中的渗透系数是含水量或基质吸力的函数，会随着水库水位的变化而处于一个动态调整的过程。因此，进行非饱和渗流参数的反演，更能体现各材料的真实参数。本文以PG砾石土心墙堆石坝为例，基于渗流原观数据进行渗流参数的反演，进而分析非饱和非稳定渗流对心墙渗流场的影响。

1 非饱和非稳定渗流参数反分析方法

1.1 非饱和非稳定渗流基本微分方程

考虑介质和土体压缩性，非稳定渗流微分方程式如下：

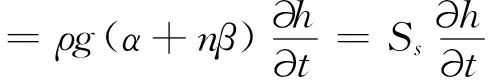
(1)

式中，kx、ky、kz—x、y、z方向的渗透速率分量；Ss—单位贮存量，Ss=ρg(α+nβ)；α—土体压缩系数；β—水体压缩系数；h—水头；n—土体孔隙率；ρ—密度；g—重力加速度。

该式既适用于承压含水层，也适用于无压渗流。饱和-非饱和渗流认为渗流几何区域全部处于水中，自由面是饱和区与非饱和区的分界线，边界水位变化时，渗流场水头的变化是通过饱和区与非饱和区的流量交换实现。非饱和非稳定渗流微分方程如下：

(2)

式中，Q—单位时间内在垂直方向从单位体积含水层中流入或流出的水量；mw—土中水的质量；γw—水容重；y—位置水头。

1.2 BC&BC非饱和渗流本构模型

土的透水性和土的饱和度密切相关，人们将土的饱和度Se随基质吸力的变化定义为土水特征曲线，将土的渗透系数随基质吸力的变化定义为渗透系数函数。基质吸力指的是土体中的毛细作用，当土体饱和时基质吸力为零，渗透系数Ks为常数，随着基质吸力的增加，渗透系数呈非线性减小。BC&BC模型是最为常用的非饱和渗流本构，其土水特征曲线和渗流系数函数的数学方程见公式(3)—(4)所示。

(3)

(4)

式中，h—吸力水头；hb—进气压力水头；λ—土的孔径分布指数。

1.3 渗流参数反演方法

对于非饱和渗流模型的参数反分析，通过建立响应面代理模型，代替数值模拟中大坝的渗透参数与有限元计算渗压效应量之间的响应关系，然后基于代表性时刻水位原观渗压监测数据与变形响应面模型的关系，构建目标函数，进行渗流参数寻优。本文采用多目标优化求解目标函数，通过心墙上区和心墙下区的两个目标函数，考虑了渗压与自身区域材料特性的关系，使目标监测点均能很好地逼近实测值。基于最小二乘法的原理，可构建参数反分析的目标函数：

(5)

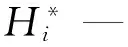
响应面法是数学理论和统计技术的结合，用于建模分析受多个变量影响的问题，其目的是优化响应。通过构建响应面方程能有效的替代大量复杂繁琐的数值模拟计算，可大幅减少工作量，使目标函数的求解过程相对简化。本文以心墙渗流参数和代表性时刻水位对应渗压主成分作为变量拟合响应面方程。采用不含交叉项的3次多项式进行构建，其形式如下：

(6)

式中，H(x)—正交试验样本对应有限元模拟的渗压；ai、bi、ci、e—响应面方程系数，通过统计回归拟合得到；xi—第i个反分析参数的取值；n—待反演的目标参数个数。

1.4 基于NSGA-Ⅱ多目标遗传算法

基本遗传算法是简单地认为个体适应度高更适合遗传优良的基因，而基于带精英策略的非支配排序(NSGA-Ⅱ)多目标遗传算法的评优机制则不同。多目标函数中每个目标函数均可得到一个适应度值，但不能同时最优，因此其解呈现为Pareto解集，其中任意两个解之间没有绝对优劣。

基于NSGA-Ⅱ多目标优化的主要步骤如下，具体流程图如图1所示。

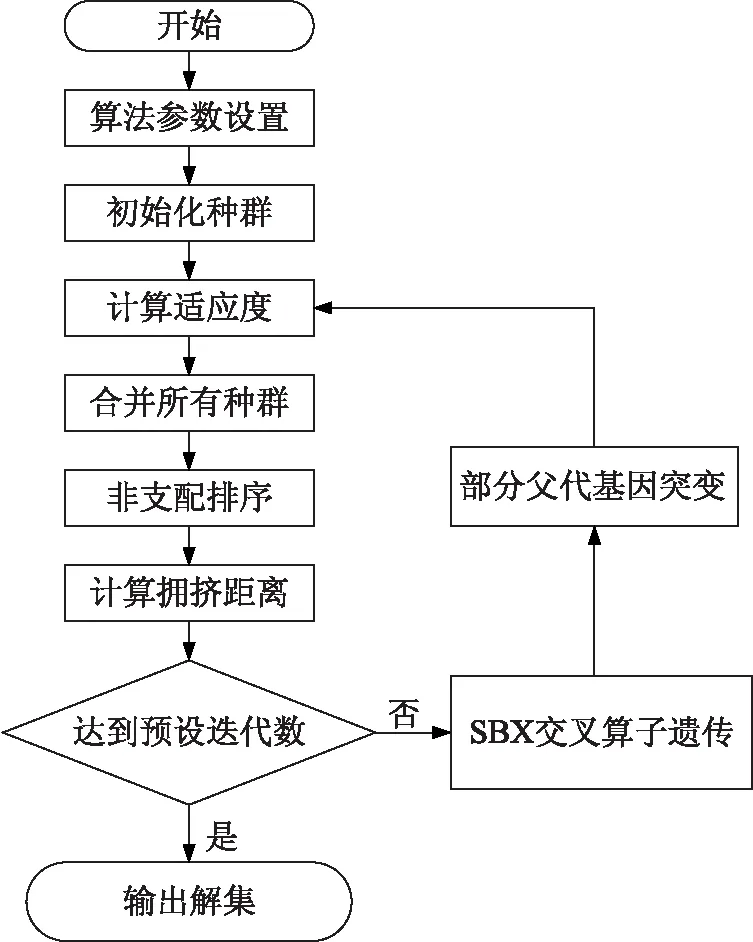
图1 NSGA-Ⅱ算法的基本流程

(1)初始化：设定待优化参数集的搜索范围，结合正交设计与随机补充的个体形成初始种群。

(2)适应度：计算每个新个体的适应度，父代个体与后代种群合并以保证优良基因不丢失。

(3)非支配排序：遍历所有个体支配关系，进行非支配排序。

(4)拥挤距离计算：计算同一层中各个个体的拥挤距离。

(5)停止准则：若达到预设迭代数，则输出当前非支配前沿，并停止反之继续。

(6)选择准则：选择非支配序小、拥挤度大的个体。

(7)交叉准则：通过SBX交叉算子遗传父代基因给子代。

(8)变异准则：为避免局部最优和过早收敛，将部分父代基因突变来增加搜索范围。

(9)迭代循环：转至第②步。

2 PG砾石土心墙堆石坝非饱和渗流参数反演

2.1 工程概况

PG水电站是一座以发电为主，兼有防洪等综合利用效益的大型水电工程。拦河坝型为砾石土心墙堆石坝，主要包含砾石土心墙、反滤层、过渡层、堆石区。在心墙上游和下游分别设置双层反滤层，反滤层与上、下游坝壳堆石之间设有过渡层。坝顶高程856.00m，最大坝高186.00m。水库正常蓄水位850.00m，校核洪水位853.78m。坝基防渗采用墙幕结合的形式，设主、副两道混凝土防渗墙，副墙位于主墙上游侧，防渗墙底设防渗帷幕，防渗墙与心墙及基岩防渗帷幕共同构成主防渗平面。其典型河床0+240断面如图2所示。

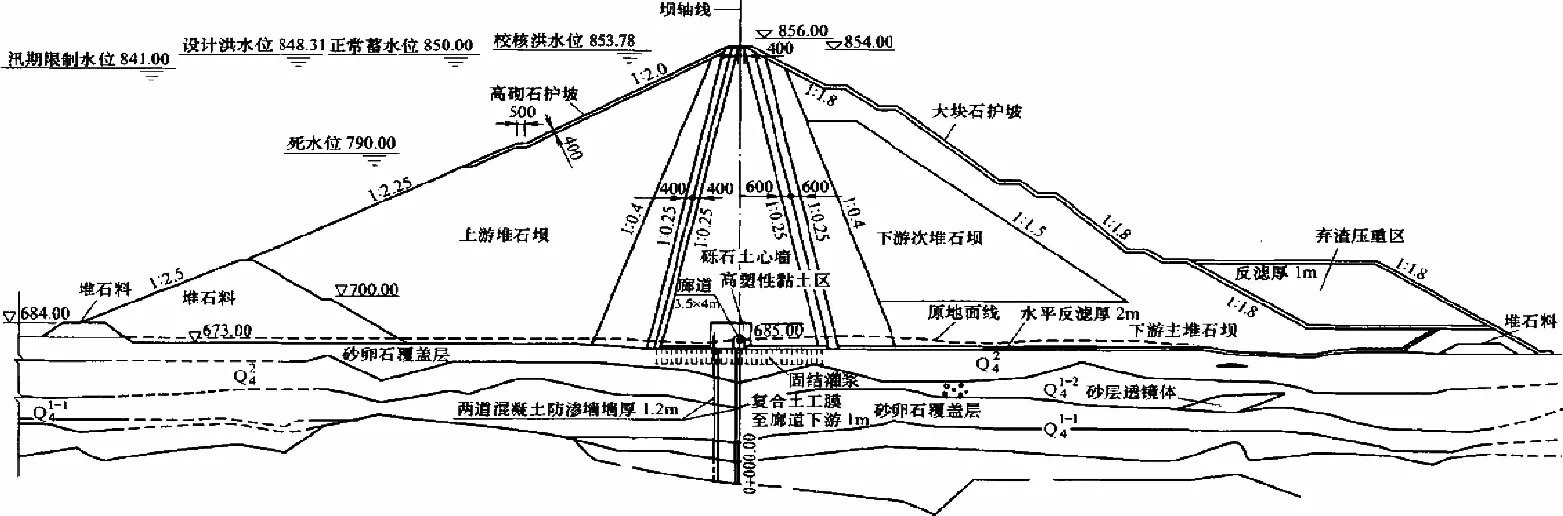
图2 PG水电站河床0+240断面示意图

2.2 有限元模型

根据坝体结构轮廓尺寸、材料分区和坝址地形地质条件等资料，本文选取大坝0+240断面，建立二维有限元模型。根据该断面渗压测点位置在有限元模型中布置相应结点，以便于提取渗压计算结果。有限元模型的模拟范围为：自建基面向下延伸2倍坝高，上下游方向自坡脚分别延伸2倍坝高。整个有限元模型共划分为11555个单元。坝体分为8个区域，其中心墙以历史最低水位为分界，分为心墙上、下区。有限元分析模型如图3所示。坝体和坝基各类材料的设计渗透系数见表1。

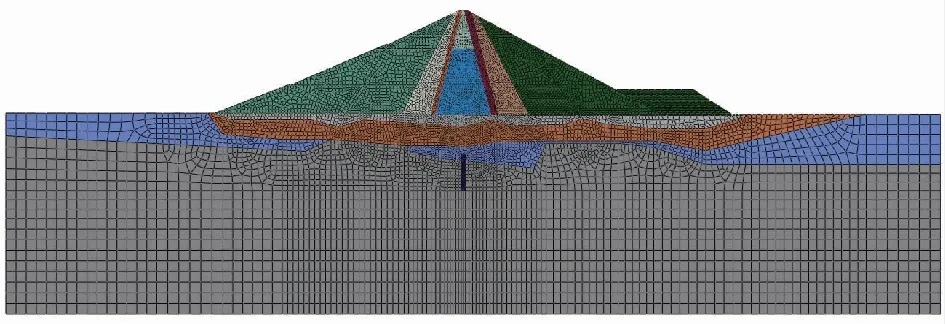
图3 PG砾石土心墙堆石坝0+240断面各分区有限元网格

表1 坝体及坝基各区材料渗透系数 单位：cm/s

2.3 心墙渗流参数反演

通过敏感性分析，本文选取5个参数进行反分析，分别为心墙上、下区和弱风化基岩的渗透系数以及两个非饱和土体参数hb和λ。选用2014年的上游库水位输入有限元进行非稳定非饱和渗流场的连续计算，分别得到每组样本对应的各特征点的渗压值。

将上半年作为拟合段，均匀选取时间控制点进行响应面拟合。下半年作为预测段，用于验证反分析结果的适用性。拟合段和预测段各有6个时间控制点。采用不含交叉项的3次多项式，对每个测点渗压在各个时间节点进行响应面方程拟合，其复相关系数均大于0.98，表明所构建的响应面代理模型对该工程的渗压效应量拟合效果良好，可用于之后的渗流参数反演。选取渗压计特征点位置如图4所示，上游水位历时曲线及时间控制点如图5所示。测点拟合选用P83进行展示，拟合情况如图6所示。

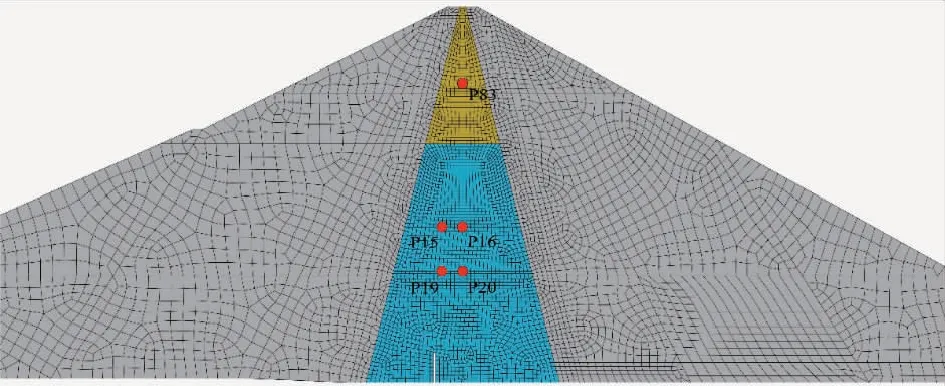
图4 PG心墙堆石坝心墙特征点示意图

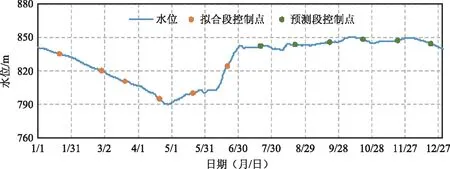
图5 2014年PG堆石坝库水位历时曲线

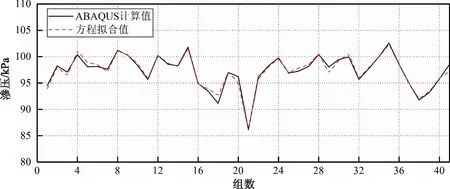
图6 P83渗压响应面模型拟合

根据渗压测点响应面代理模型及对应的原观监测渗压数据，采用归一化的方法，通过每个测点不同时间控制节点对应的实测渗压值和响应面方程模拟渗压值的相对误差平方和构建目标函数。采用多目标优化对目标函数求解，得到包含2000组解的Pareto解集。通过Pareto解集与反演参数设计值隶属度函数寻优获得PG堆石坝心墙非饱和渗流参数反分析结果，见表2。

表2 参数反分析结果

将解代回有限元模型进行数值模拟计算，拟合效果选取心墙上区测点P83和心墙下区测点P20进行展示，如图7—8所示，与实测值对比的误差分析见表3。结果表明，代回有限元模型后可以较好地拟合实测渗压的变化趋势，拟合精度高，各测点的平均绝对误差均值为10.1kPa，平均相对误差均值为1.71%。

图7 P83渗压反演与实测值对比

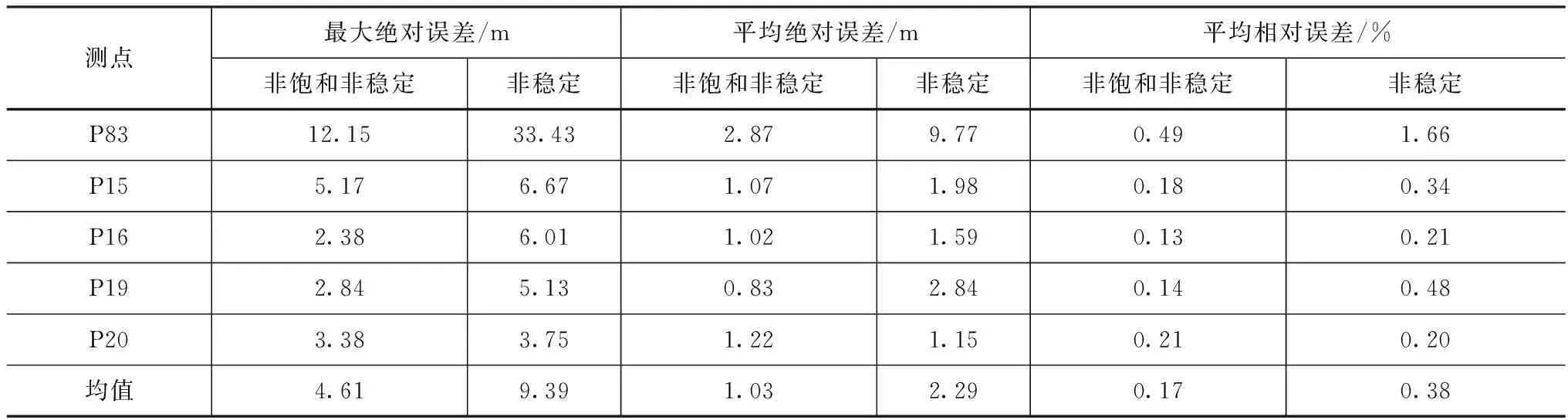
表3 参数反分析有限元结果误差分析

对比非饱和非稳定渗流与饱和非稳定渗流，非饱和特性对心墙下区渗压影响较小，两种渗流的心墙下区测点的平均绝对误差分别为1.03、1.89m，但是对心墙非饱和区渗压影响较大，在水库水位下降过程中，两种渗流的平均绝对误差分别为2.87、9.77m，饱和非稳定渗流的最大绝对误差达到33.43m。因此非饱和渗流有限元模型不仅能反映饱和区渗流变化，也能反映非饱和区渗流变化，使心墙渗流的模拟更符合实际情况。

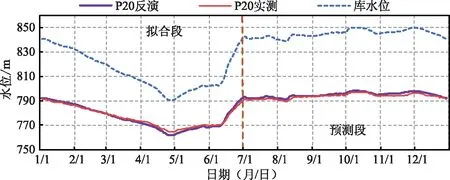
图8 P20渗压反演与实测值对比

2.4 非饱和渗流特性分析

根据反分析获得的参数进行饱和渗流与非饱和渗流的渗流场孔隙水压对比，选取2个典型时刻绘制对应时刻的孔压云图如图9所示。

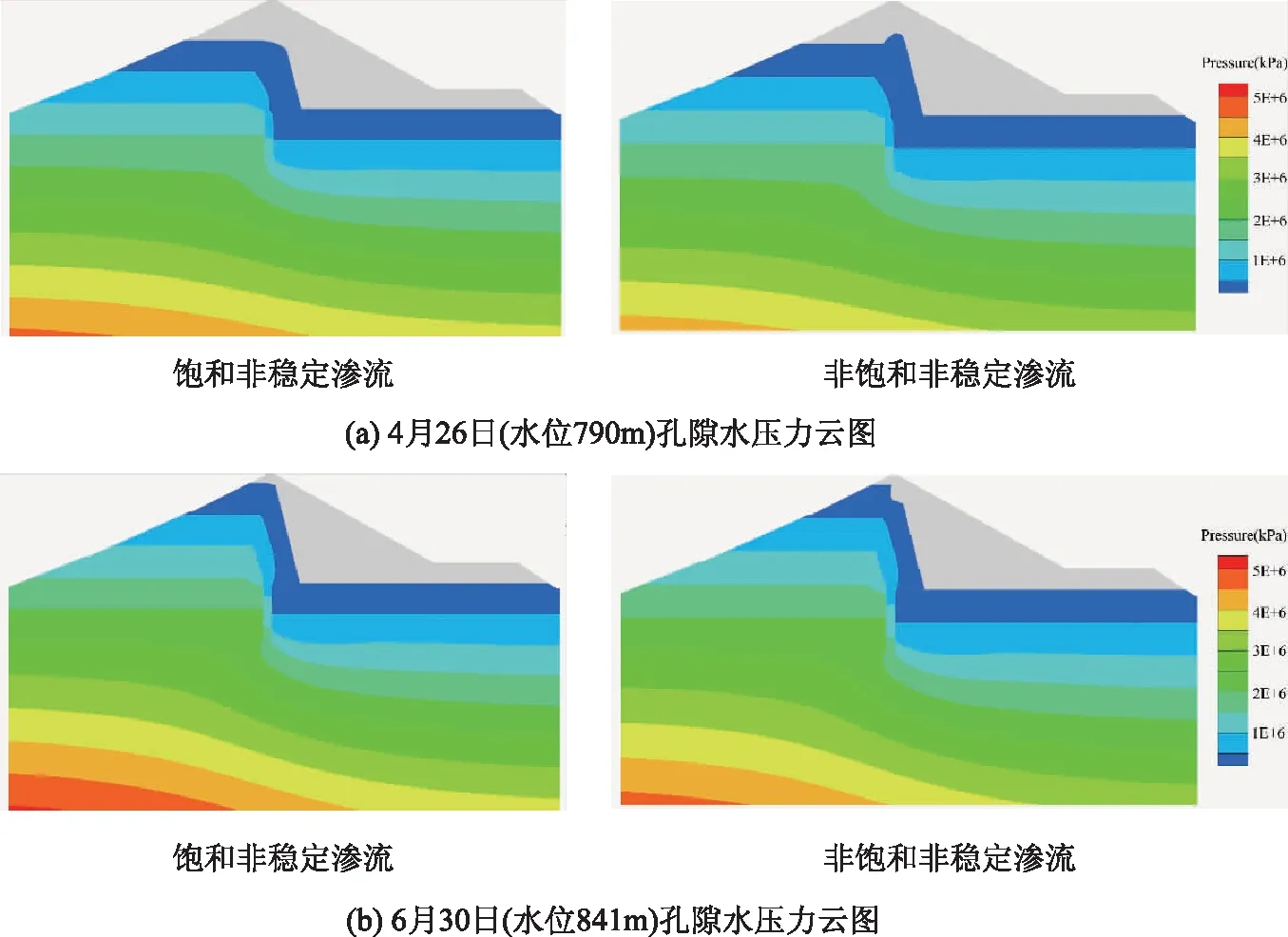
图9 典型时刻的饱和非稳定渗流与非饱和非稳定渗流孔压

不考虑非饱和特性的非稳定渗流，浸润面变化基本同步于水库水位变化，在心墙下游面迅速折减。考虑非饱和特性后，上游水位下降时，孔隙水压力不能及时消散，心墙浸润线变化滞后于水位的降低，出现心墙浸润线高于水库水位。水位上升时，存在由非饱和状态至饱和状态的过渡，心墙浸润线变化滞后于水位的上升，且心墙内浸润线升至与水库水位相同稳定浸润线需要经过一段时间。

出现上述现象是由于心墙上区受到土体基质吸力影响。基质吸力随土体饱和度降低而增加，心墙渗透系数随吸力的增加，呈非线性的降低，上游水位下降时心墙内水分由于基质吸力来不及消散而滞留在心墙内，堆石区不考虑非饱和特性且渗透系数较大，当堆石区浸润线与水位保持同步时，心墙内仍然维持相对较高的浸润线，呈现“上凸”的抛物线形状。这种情况容易引起心墙材料容重改变，带来的非稳定渗流力造成土体颗粒之间有效应力减小，进一步导致土的抗剪强度降低，最终危机坝体稳定性。水位降落速度越快，心墙浸润线相对位置越高，其非稳定渗流力越大，对稳定性影响也越大。

计算典型时刻堆石坝心墙和防渗墙的渗透坡降并绘制云图，如图10所示。结果表明心墙孔压和渗透坡降分布均匀，渗透坡降较大值出现在心墙中下部和防渗墙中上部，心墙出逸点附近渗透坡降为2～3，出现的心墙最大渗透坡降为2.72，小于心墙允许渗透坡降3。主、副防渗墙渗透坡降基本相近，防渗墙最大坡降出现在主防渗墙上部，出现的防渗墙最大渗透坡降为88.55，小于防渗墙允许渗透坡降120。

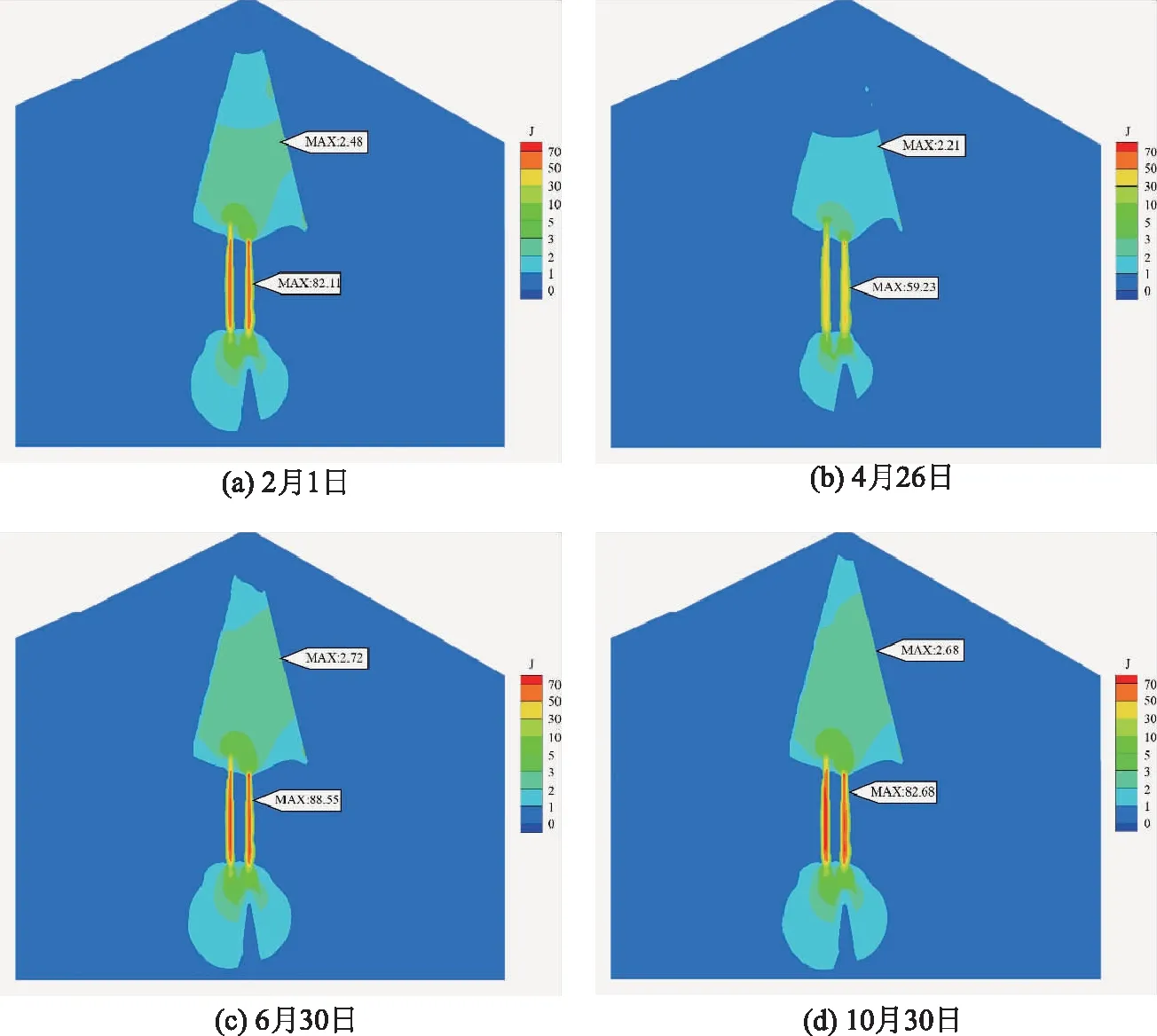
图10 非饱和非稳定渗流坡降云图

3 结语

本文依托PG砾石土心墙堆石坝工程，构建非饱和非稳定渗流模型。基于堆石坝渗流原观数据和响应面代理模型，采用NSGA-Ⅱ多目标遗传算法，进行渗透系数和非饱和特性参数的反演，其结果都在合理范围内。反演结果表明，反演得到的渗流参数对于心墙上区渗压变化的拟合情况较为准确，能整体反映大坝心墙渗压场的变化情况。考虑心墙材料的非饱和特性，引入土-水特征曲线及渗透系数函数模型，更正了非饱和区渗透系数恒定不变从而导致非稳定渗流求解的不准确性，使心墙非稳定渗流的模拟更加符合实际情况。