基于引力搜索算法的混合零空闲置换流水车间调度
赵 芮,顾幸生
(华东理工大学 化工过程先进控制和优化技术教育部重点实验室,上海 200237)
0 引 言
零空闲置换流水车间调度问题(No-idle Permutation Flow Shop Scheduling Problem, NPFSP)广泛存在于陶瓷熔块生产、玻璃纤维加工、铸造、集成电路生产和炼钢等现代工业中。关于调度问题中零空闲概念的提出者在学术界存在争议[1-2],一部分学者认为是Adiri和Pohoryles于1982年考虑了求解总流水时间的带零空闲约束的流水车间调度问题;另一部分学者认为是Babushkin等人早在1975年就尝试以最小化makespan为目标,对具有零空闲约束的类似流水车间的调度问题进行了研究。但毋庸置疑的是,自此NPFSP的研究受到了广泛的关注,并在近年取得了很大的进展。
然而,这种假设所有机器都是零空闲的情况较为少见,实际生产过程中更多的是混合零空闲调度问题,即只有部分机器受到零空闲状态的约束。目前国内外已经有学者对混合零空闲置换流水车间调度问题(Mixed No-idle Permutation Flow Shop Scheduling Problem, MNPFSP)进行了研究。PAN等[3]首先对混合零空闲流水车间进行研究,提出了一种有效的迭代贪婪(Iterative Greedy, IG)算法来最小化makespan;CHENG等[4]将分布式调度运用到混合零空闲流水车间中,并提出一种新的基于云理论的IG算法,用于最小化makespan;ROSSI等[5]针对存在序列相关准备时间的混合零空闲流水车间,开发了一种新的有效的启发式算法。
虽然对MNPFSP的研究已经取得了一些进展,但在算法求解方面还可以有更深入的研究。对于MNPFSP的计算复杂性,已被证明是NP完全问题[1,3]。因此,只有小规模的问题能通过精确算法在合理的计算时间内找到最优解,随着问题规模的逐渐增大,其复杂性呈现指数爆炸效应。构造性启发式方法虽然能在较短时间内构造出近似最优解,但难以保证解的质量。因此,近年来的研究趋势是将启发式规则与智能优化算法相结合求解调度问题,从而大大提高了智能优化算法的性能[6]。
如上所述,MNPFSP是NPFSP一个比较新的变体,成功应用于MNPFSP的智能优化算法还很少。引力搜索算法(Gravitational Search Algorithm, GSA)[7]是一种模拟自然界中粒子相互吸引的智能优化算法,已在一些生产调度问题上取得了一定成果,但目前还没有用于MNPFSP和NPFSP的求解。BARZEGAR等[8]利用GSA和有色Petri网求解最小化makespan的柔性作业车间调度问题;针对作业车间调度,吴琼等[9]提出一种协同粒子群和GSA混合算法最小化makespan,结果表明该算法较粒子群优化(Particle Swarm Optimization, PSO)算法和遗传算法(Genetic Algorithm, GA)等在求解作业车间调度问题上更具优越性。GSA作为一种随机优化算法,其原理简单,具有较强的全局搜索能力,收敛性也被证明优于粒子群优化算法、遗传算法等智能优化算法[10-12]。然而,随着种群的进化,个体受最优解吸引逐渐群聚在一起,导致GSA在进化后期收敛速度过快,无法完全覆盖所有解,寻优精度不高。因此,对GSA进行改进,并将其应用于MNPFSP中,具有重要的研究意义。
针对混合零空闲置换流水车间问题的特点,本文采用GSA解决以最小化总流水时间为目标的MNPFSP,提出一种基于可变迭代贪婪(variable Iterative Greedy, vIG)的引力搜索算法,利用vIG对解空间较强的局部开发能力来改善GSA的精度。为了将GSA算法用于离散的调度问题,使用ROV规则进行编码。算法的初始化阶段,融入NEH(Nawaz-Enscore-Ham)启发式规则,以获得较好的初始解,提高算法的搜索效率;针对传统GSA随着种群的进化,个体受最优解吸引逐渐群聚在一起导致寻优精度不高的问题,将具有较强局部搜索能力的vIG算法[13-14]与GSA相结合,提高了求解质量;为了加快vIG算法的收敛速度、提高其求解精度,加入参照插入方案(Referenced Insertion Scheme, RIS)[15-16];而针对vIG算法容易陷入局部最优的缺陷,引入模拟退火思想[2,15],以一定概率接受劣解,以增加算法多样性。实验表明,采用本文提出的基于可变迭代贪婪的引力搜索算法解决MNPFSP是可行且有效的。
1 混合零空闲置换流水车间调度问题
MNPFSP描述如下:n个工件J={1,2,…,n}按照相同的顺序在m台机器M={1,2,…,m}上进行加工。在任意时刻,每台机器最多加工一个工件,每个工件最多只能被一台机器加工[17]。为了遵循零空闲的约束,机器i加工第j个工件的开始时间必须等于第j-1个工件的加工完成时间。换句话说,每台机器加工任意两相邻工件时没有空闲时间。
MNPFSP是NPFSP和置换流水车间调度问题(Permutation Flow Shop Scheduling Problem, PFSP)的混合,是指在加工过程中,有的机器处于零空闲状态,有的机器不处于零空闲状态。用π={π1,π2,…,πl,…,πn}来表示一个工件排序,用[l]来表示排序中处于位置l的工件,即πl;用pi,[l]来表示工件πl在机器i上的加工时间;Si,[l]和Ci,[l]分别表示工件πl在机器i上加工的开始时间和完成时间;ai表示工件πl在机器i上开始加工前的总延迟时间。将具有零空闲状态的机器集合记为M′,则MNPFSP的公式如下[3]:
(1)
(2)
(3)
(4)
(5)
调度问题的目标是求得一个工件加工序列π,使各工件按照该序列加工时总流水时间(Total Flow Time, TFT)最小,目标函数TFT可表达为:
(6)
2 引力搜索算法
GSA是伊朗的克曼大学教授RASHEDI等[7]于2009年提出的一种新型智能优化算法,算法灵感来源于粒子受万有引力的作用。它可以理解为众多的粒子向具有最大惯性质量的粒子不断靠近的过程。算法中,种群由惯性质量各不相同的粒子组成,每个粒子的位置对应问题的一个解,指引算法进行迭代优化的引力和惯性质量是由适应度函数值确定的。当种群中出现惯性质量大的粒子时,其他粒子都朝着惯性质量大的粒子运动,从而使算法收敛到最优解。
假设在n维搜索空间中有NP个粒子,则第i个粒子的位置表示为:
(7)
在第t次迭代时,种群中第j个粒子作用在第i个粒子上的引力表示为:
(8)
式中:Mi(t)和Mj(t)分别表示被作用粒子i和作用粒子j的惯性质量;Rij(t)为两个粒子i和j之间的欧氏距离;ε为一个很小的常量;G(t)为第t次迭代时的引力系数,它随时间逐渐减小以控制搜索精度,是初始值G0和迭代次数t的函数:
(9)
式中:α为控制G(t)衰减速率的常数;T为迭代总次数。一般G0=100,α=20。

(10)
(11)
式中randj是范围在[0,1]之间的随机数。
粒子的惯性质量可根据种群的适应度值fit来计算:
(12)
(13)
worst(t)和best(t)分别表示当前种群中适应度的最差值和最好值,由于本文求解的是最小值问题,定义worst(t)和best(t)为种群中适应度最大值和最小值。
GSA算法中,每一次迭代种群的速度和位置更新公式为:
(14)
(15)
式中randi是区间[0,1]中的均匀随机变量。
3 求解MNPFSP的贪婪引力搜索算法
3.1 编码方案与ROV转换
由于标准的GSA是处理连续问题的优化算法,其连续编码方案不能直接用于求解离散的MNPFSP,而IG算法是基于工件排序直接进行编码的,需要将两者的解空间进行转换。本文基于升序排列(Ranked-Order-Value, ROV)规则将多维空间的连续粒子位置与工件排序进行一一对应映射,其原理如表1所示。将粒子的位置分量按从小到大的顺序排列,最小的位置分量赋值为1,次小的位置分量赋值为2,以此类推,从而形成完整的工件排序。如果分量值相同,则粒子维度较小的赋予分量值较小,粒子维度较大的赋予分量值较大。表1中粒子Xi的工件排序为πi=(4,3,2,6,1,5)。
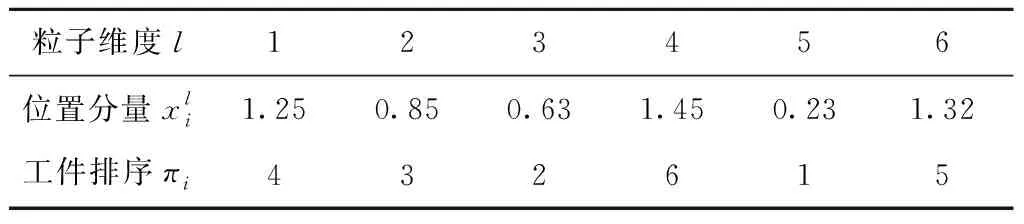
表1 粒子Xi的ROV转换
3.2 种群初始化
好的初始种群可以有效加快收敛速度并提高解的质量。为了提高搜索效率,使解既有较高的质量又有较大的发散度,在初始化中引入NEH启发式规则[18]产生第一个解,其余解随机生成。
NEH启发式规则由排序和插入两个阶段组成,其基本操作如下:

步骤2按总加工时间Pj的降序,对工件进行排序。
步骤3取k=1和k=2两个工件进行排序,并选择总流水时间小的那个排序作为当前部分序列。
步骤4k:=k+1,将第k个工件插入当前部分序列(包含k-1个工件)所有可能的k个位置中,得到k种不同的工件排序,然后在其中选出使总流水时间最小的排序作为当前部分序列(包含k个工件)。
步骤5如果k=n,则停止,否则转步骤4。
3.3 贪婪引力搜索算法
GSA算法具有较强的全局搜索能力,种群多样性也很好,但其收敛速度过快,不能完全覆盖所有解,算法精度不高。本文提出的贪婪引力搜索算法(Greedy Gravitational Search Algorithm, GGSA)以GSA为主框架,在进化后期(即最优解连续L代不再变化时),加入局部搜索能力强的带RIS的可变迭代贪婪算法(vIG_RIS),能够很大程度上提高GSA算法的寻优精度,从而改善收敛效果。
vIG_RIS算法由vIG算法[13]和RIS[16]局部搜索两部分组成,伪代码如图1所示。vIG_RIS实质上是迭代贪婪(IG)算法的一种改进。RUIZ等[19]研究表明,IG算法对于求解离散的调度问题十分有效。并且,该算法的破坏重构(destruct construct)机制直接基于工件排序进行,无需编码、解码,更适合离散的调度问题。由此可以看出,引入vIG_RIS算法是十分有效的。

IG中毁坏工件数d是一个比较关键的参数,若d太小,则算法搜索范围较小、收敛较慢;若d太大,则会影响算法效率。因此,一般选取固定的单一值[20]。vIG算法在此基础上引入了变邻域的概念,使得在构造新解的过程中原本固定的参数d可变,从而增加了解的多样性。当解没有被改进时,d从1逐次递增到n-1;一旦解有所改进,则将d再次固定为d=1,从头开始搜索。
图1中,Destruction和Construction两个阶段用来生成新的解π1。在Destruction阶段,首先从π中移除随机选择的d个工件,产生πR和πD两个排序,其中πR包含d个移除工件,πD包含剩余的n-d个工件;在Construction阶段,将πR的第一个工件插入πD中,产生n-d+1个部分解,选择其中最优解用于下一次迭代,接下来将第2个工件插入πD中,……,直至πD中包含n个工件,形成完整的调度解。
vIG_RIS算法在vIG算法的基础上对解π1进行了基于插入和交换的随机局部搜索RIS,由此产生了一个新的解π2。当π2是一个劣解时,使用OSMAN等[21]提出的模拟退火的收敛判据以概率exp{-(f(π2)-f(π))/Temp}接受它。通过该方式,当前解在搜索过程中获得了一些劣解而得以多样化,以此来期望逃离局部最优。
(16)
式中:Temp为恒定的温度;τ为调整温度Temp的冷却系数。
如图2所示为RIS的程序伪代码。在RIS中,πref为参照排序,它是迄今为止得到的最优解。举例来说,假设πref=(3,1,5,2,4)且当前解π=(4,2,5,1,3),RIS首先在π中找到工件3,从π中移除工件3并将其插入π的所有可能位置。接下来,在π中找到工件1,从π中移除工件1并将其插入π的所有可能位置。重复该过程,直至πref的所有工件均被参考过。可以看出,RIS的主要概念是:工件移除由参照排序引导而不是随机选择。

vIG_RIS算法在IG的基础上,增加了可变的邻域结构,使得算法在搜索过程中能更多地探索解空间,有更大可能找到更优解,使解的多样性得到了改善。而且该算法以一定概率接受劣解,能在一定程度上避免陷入局部最优,还通过RIS增强了局部搜索能力,但是其寻找解的过程较为缓慢。本文提出的GGSA算法在GSA算法迭代的后期引入vIG_RIS算法进行局部搜索,vIG_RIS的寻优开始于当前的最优解,利用vIG_RIS优秀的局部开发能力帮助其提高寻优精度,然后再回到GSA算法的主体中继续迭代。这样既可以平衡算法的收敛速度,又可以提高寻优精度,从而提高解的质量,取得好的收敛效果。
GGSA算法的总体流程如图3所示。其中L为最优值不变的最大代数,Fbest为当前最优适应度值,当Fbest经过L代都没有发生变化时,算法转入vIG_RIS搜索。若vIG_RIS搜索得到的解的适应度值小于Fbest,则将其替换为种群X中随机的一个粒子。

4 仿真实验
算法基于MATLAB 2015实现,在处理器为2.40 GHz、内存为64.0 GB的PC机下运行。为了检验GGSA算法求解MNPFSP的有效性,本章在正交实验确定了参数的基础上,采用Taillard Benchmark问题[22]中的9种不同规模的共90个典型算例进行测试,并将仿真结果与DFWA-LS算法[23]、vIG算法[13]以及IGeDC算法[3]进行比较。
由MNPFSP的实际生产过程可知,第一台机器一般处于零空闲状态,最后一台机器一般不处于零空闲状态,而大多数工厂生产中需要零空闲约束的机器占比较少。因此,在仿真测试中设置两台机器处于零空闲状态:第一台机器和随机选择的除第一台和最后一台机器外的中间一台机器(用符号Mset来表示)。实验中每个算例对应的Mset分别进行如下设置:m=5时,每种规模下的算例按从小到大的序号排列,其Mset依次为[4 2 2 4 3 4 3 3 2 4];同样地,m=10时,Mset依次为[3 5 8 4 7 5 6 9 4 6];m=20时,Mset依次为[11 15 4 7 10 5 13 17 6 18]。不同算法对比时,每个算例中处于零空闲状态的机器编号是相同的。
为确定算法中最大迭代次数T、种群规模NP以及参数G0、α、τ、L和tmax的取值,利用正交设计方法,将每个参数都设为3个因子,每个因子设置3个不同水平,选择L18(37)正交表进行正交实验,如表2所示。正交实验在算例Ta043上进行,每种参数组合各进行20次仿真,正交实验结果如表3所示。以相对百分比偏差(Relative Percentage Deviation, RPD)的平均值作为响应变量(Response Variable, RV):RPD=(TFTi-TFT*)/TFT*×100%,其中TFTi为第i组参数组合下得到的总流水时间值,TFT*为所有参数组合下算法运行得到的总流水时间最优值。

表2 正交设计因子水平表
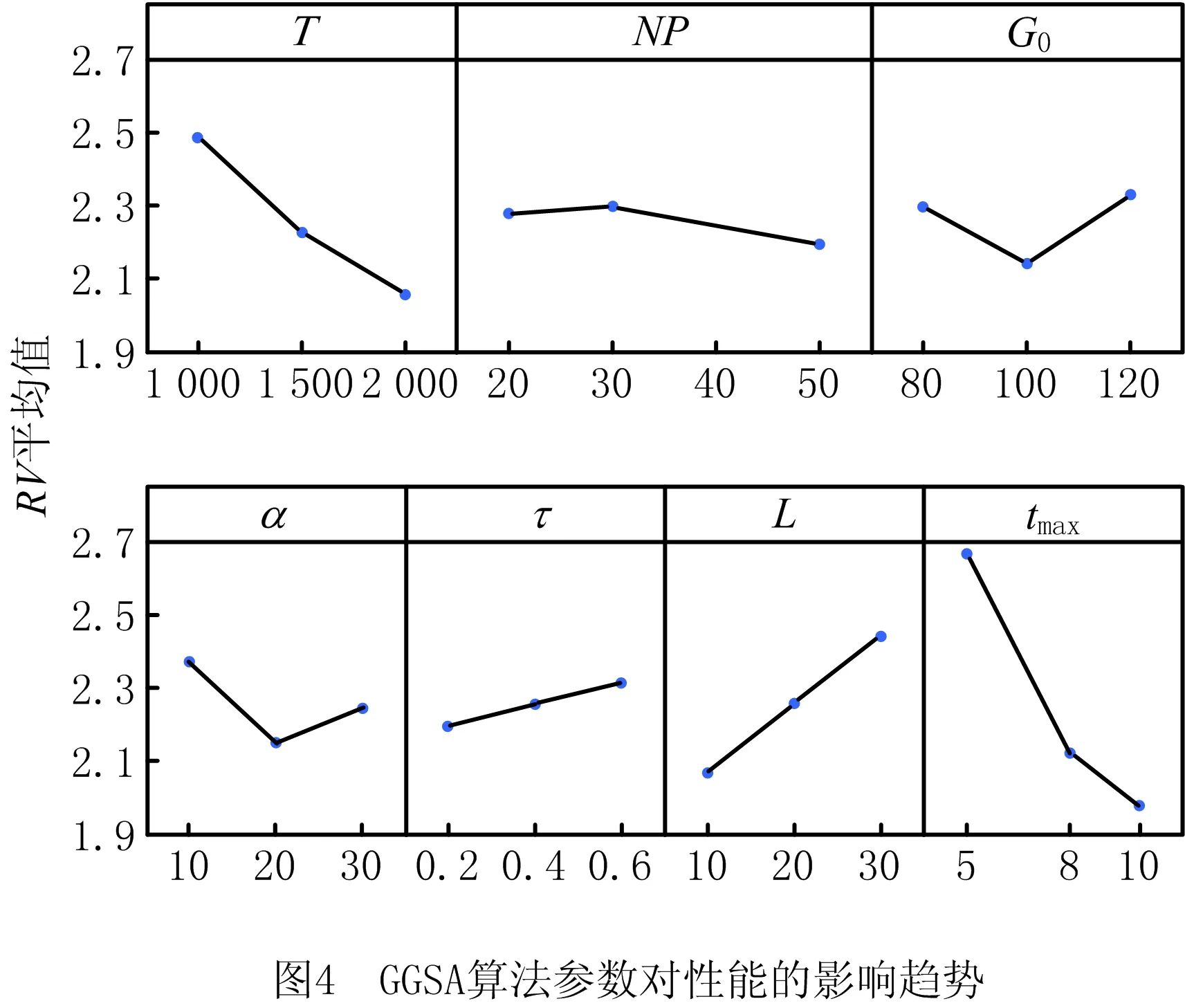
由正交实验结果可见,参数对算法性能的影响程度从大到小依次为:tmax,T,L,α,G0,τ,NP。由图4可见,参数tmax和T对算法性能影响的水平趋势相同:较大的迭代次数有利于算法进行更深入的搜索。参数L的变化趋势表明适当减小参数L有利于算法避免早熟收敛或收敛缓慢。参数G0和α对算法性能的影响趋势也大致相同,它们对平衡算法的全局搜索和局部搜索有着重要意义,既不能太大也不能太小。参数τ和NP的极差较小,但也不能说对算法性能完全没有影响:参数τ的值要取的较小一些,如果τ的值太大,算法接受差解的概率太大,会导致算法在结束前不能找到足够好的解;而适当大的种群规模则对算法的多样性有利。基于以上分析,采用如下参数设置进行后续实验:tmax=10,T=2 000,L=10,NP=50,G0=100,α=20,τ=0.2。
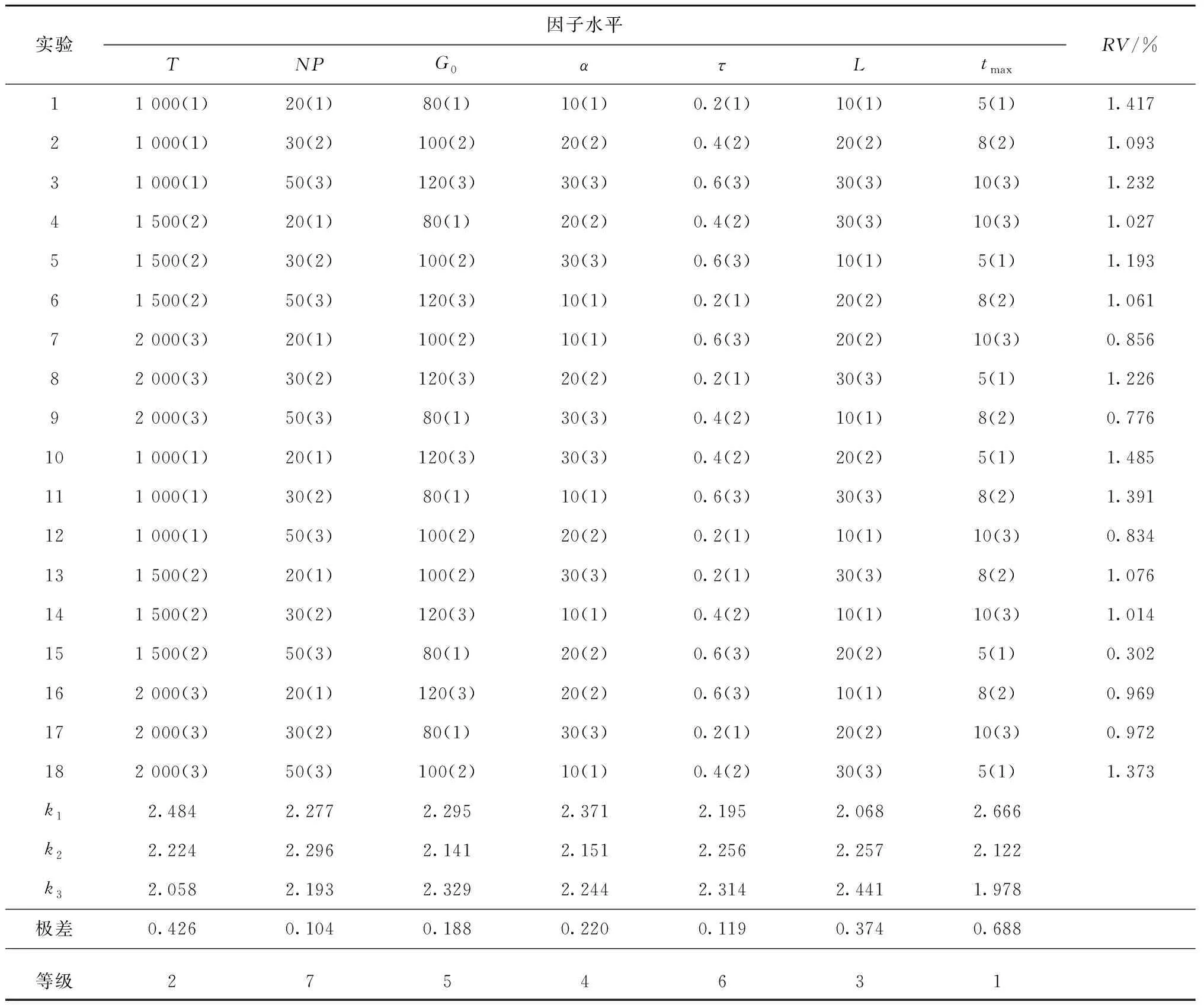
表3 算例Ta041的正交实验结果

目前研究MNPFSP的文献还非常少,尚无已知的最优解。参考文献[24]中分析比较Fm/prmu,no-idle/∑Cj问题的方法,将DFWA-LS算法、vIG算法、IGeDC算法以及GGSA算法产生的解与NEH规则产生的解进行对比分析(如表4)。为了避免测试的随机性带来的误差,每次不同的仿真都独立运行10次。结果以平均相对百分比偏差(Δavg)和标准偏差(Δstd)给出,其公式如下:
(17)
(18)
其中:N为规模相同的算例的数量;TFTi(H)表示H算法求解算例i的10次运行结果的平均值;NEHi
为NEH规则下算例i的解。

表4 GGSA算法与其他各算法的比较结果
从表4中可以看出,对比4种算法,它们的标准偏差没有统计学上的显著差异,而GGSA算法的平均相对百分比偏差的绝对值更大,所求得的总流水时间更小,即GGSA算法可较好地应用于MNPFSP,能在保证算法稳定性的情况下找到比DFWA-LS算法、vIG算法和IGeDC算法更优的解。

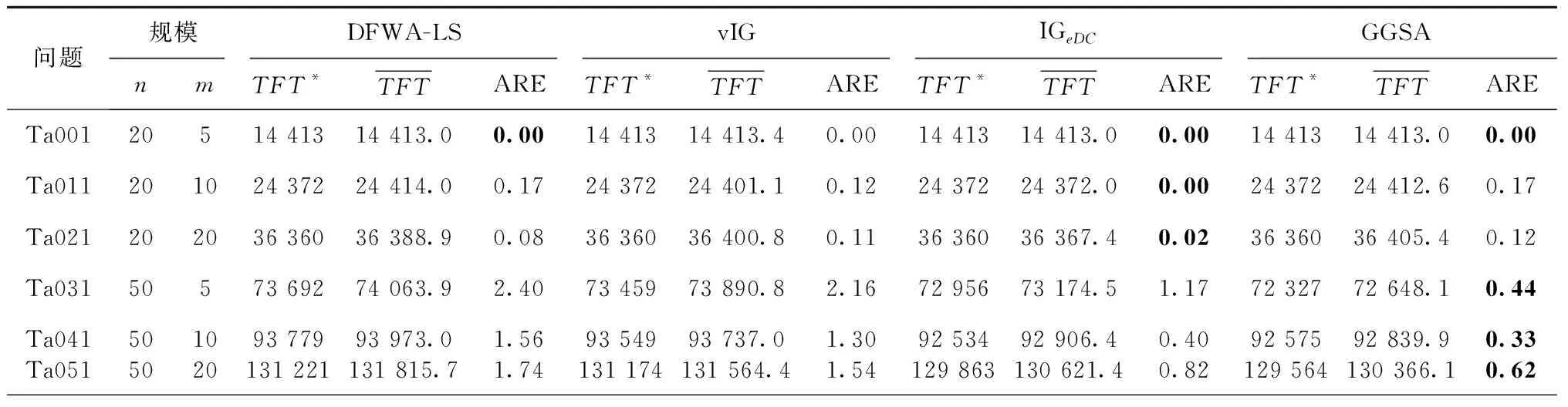
表5 平均相对误差的比较结果

续表5

综合表4和表5可以得出:对于Taillard Benchmark算例,GGSA算法的求解要优于DFWA-LS算法、vIG算法和IGeDC算法,且一般而言(排除极个别算例),随着算例规模的增大,GGSA算法的求解效果也越来越好,这充分说明了GGSA算法在求解MNPFSP上的有效性和优越性。
DFWA-LS、vIG、IGeDC和GGSA四种算法对Ta043算例的迭代收敛曲线如图6所示,由比较结果可知,DFWA-LS和vIG算法的求解效果较差、精度较低,而IGeDC算法虽然收敛较快,但容易陷入局部最优,GGSA算法由于在进化的后期引入vIG_RIS,能够在GSA找不到更优解时加大对极值点邻域的开发,提高其搜索精度,得到令人满意的解。
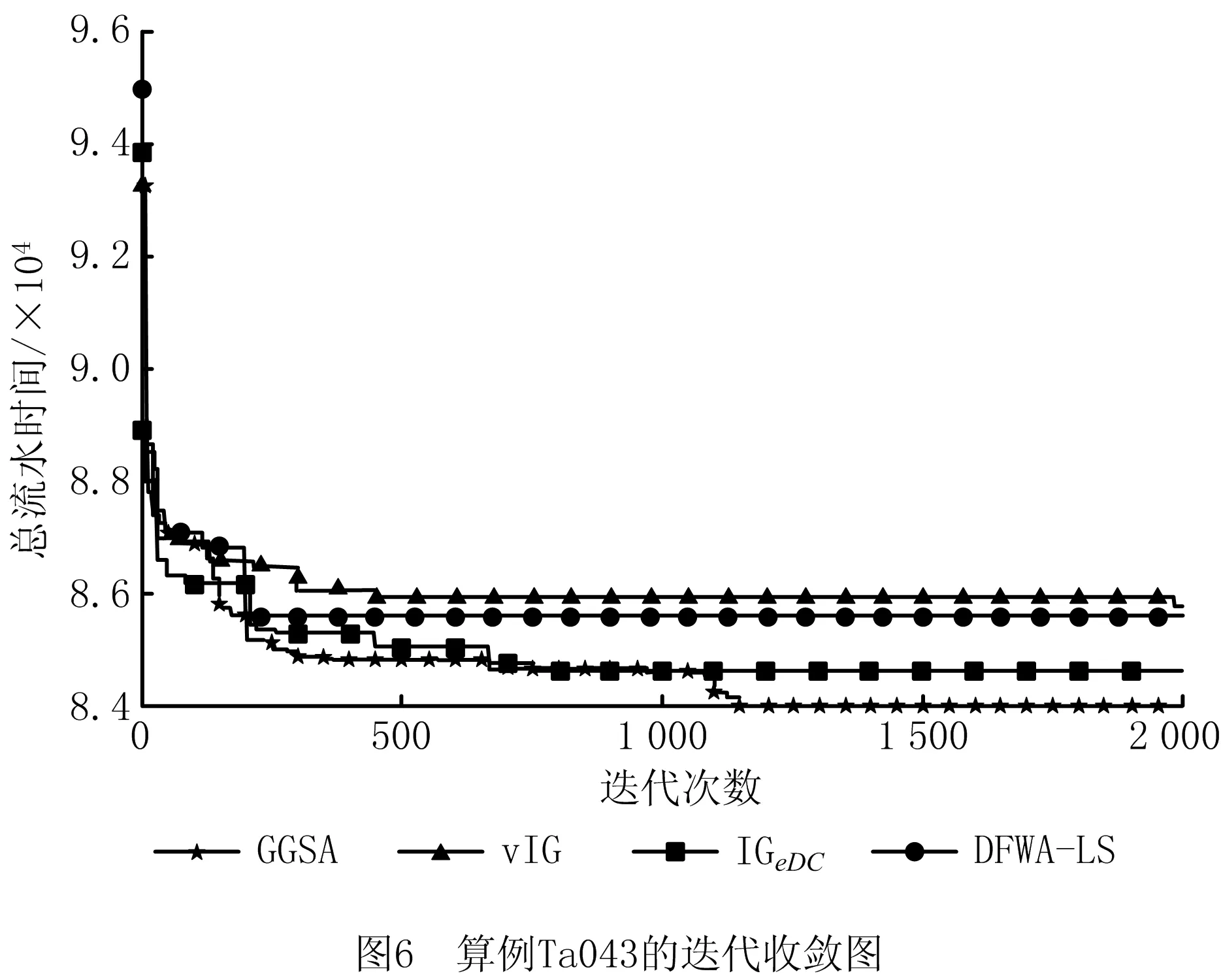
5 结束语
本文将引力搜索算法应用于求解以最小化总流水时间为目的的混合零空闲置换流水车间调度问题。在引力搜索算法的基础上,引入具有较强局部开发能力的vIG算法,并对原引力搜索算法初始解的产生方式、vIG算法的局部搜索进行了改进,提出一种贪婪引力搜索算法(GGSA),使其求解调度问题的精度更高,能够得到更高质量的解。针对零空闲机器数量较少的MNPFSP,在Taillard Benchmark算例上测试了本文提出的GGSA算法,并通过与DFWA-LS、vIG和IGeDC算法的对比,验证了GGSA算法在求解MNPFSP上的有效性和优越性。下一步研究包括以下几个方面:考虑将算法应用于更广泛的调度问题以及其他的优化目标;考虑MNPFSP中零空闲机器的其他情况。

