基于命中概率模型的反舰导弹—目标分配方法研究*
白建保 尹 栋 谢海斌 庄东晔
(国防科技大学 长沙 410073)
1 引言
在海上舰船作战中,能够根据战场态势,快速决策、动态分配打击目标是提升作战效能的关键。在多舰对抗的导弹与目标分配问题中,主要考虑两方面内容:弹目关系和分配算法。一方面,在弹目关系上存在着多种因素会对分配结果产生影响,如舰船和目标初始状态、导弹命中概率、导弹毁伤概率等。针对这方面的研究包括:张邦楚等提出了一种基于蚁群优化的多弹协同目标分配算法[1],建立包含距离、速度、导弹发射角度在内的弹目优势模型,但是模型比较简单,没有考虑导弹运动影响;刘树衎等提出了依照弹目之间的角度关系为目标平均分配导弹[2],这种分配方式只利用了弹目角度信息,没有考虑导弹运动等其他因素;张滢等综合考虑攻击、资源和毁伤概率等约束条件,建立了多目标优化的分配模型[3],比较复杂,不易计算。另一方面,解决此类问题的分配算法包括:遗传算法[4]、模拟退火算法[5]、蚁群算法[6]等。
导弹只有命中目标后才能产生毁伤,因此导弹命中概率是影响分配结果的重要因素。本文综合考虑模型复杂度和精确度两方面内容,根据导弹和目标的初始位置、速度、运动方向等信息,建立了一个带轨迹约束的导弹命中概率模型,并在此基础上设计了多轮动态分配算法,进行仿真实验。
2 问题描述
在舰队作战中时,当探测到敌方位置和运动状态后,需要快速地制定攻击分配方案。其整个问题解决流程如图1所示。

图1 问题解决流程
导弹未发射时与舰船的状态相同,假定有n枚导弹(M1,M2,…,Mn),m个目标(T1,T2,…,Tm),导弹的状态信息包括位置LM、速度Vm、初射角度q;目标的状态信息包括位置LT、速度Vt、航向θt、价值Ej。
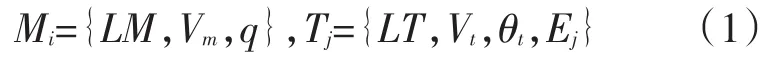
假设导弹Mi对目标Tj的命中概率为Pij,当Pij>Pa(Pa为给定阈值)时,导弹才参与分配。构建分配矩阵Dis=(Disij)n×m,每枚导弹只能够攻击一个目标,每个目标最多可以接受Tmax枚导弹的攻击,即:
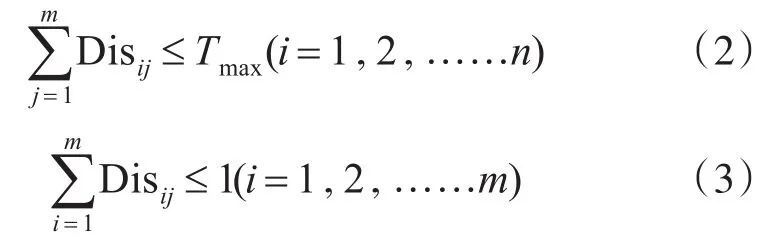
每次受到攻击时目标价值Ej会发生变化,第k轮攻击后导弹j的价值为

分配结束条件:

当进行动态分配时,导弹每打完一次,能够根据现在战场上敌我舰船的数量、舰船位置变化等情况,重新计算命中概率。假设次分配后,我方舰船出现损伤,导弹的命中概率会产生Pd的损失。第k轮分配导弹的命中概率为

分配目标是取得最好的作战效果,即使得目标价值变得最小

3 单次攻击命中概率求解模型
在反舰导弹攻击目标的过程中,目标的有效捕捉是导弹命中目标的前提,并且导弹自导命中目标的概率很高,所以一般情况下把导弹末制导雷达对目标的捕捉概率作为导弹的命中概率。
反舰导弹的飞行过程一般可以分为自控飞行阶段和自导飞行阶段[7],导弹在自控飞行阶段的终点即为末制导雷达开机点,此时弹目距离ΔR等于导弹的自导距离Rzd,如图2所示。末制导雷达的开机点与导弹的运动轨迹相关,雷达开机点的不同也会造成命中概率的变化。因此导弹的命中概率可以分为两部分计算,一是求解导弹的飞行轨迹,计算末制导雷达开机点位置;二是计算导弹对目标的命中概率Pij。

图2 导弹飞行过程示意图
在给定舰船和目标初始状态信息后,代入导弹在自控阶段运动模型计算,得出导弹和目标在自控终点的状态信息;利用此时双方的状态信息,代入命中概率模型计算,得到导弹的命中概率。下面将对每个阶段分开讨论。
3.1 反舰导弹自控飞行阶段的运动模型
反舰导弹在自控飞行阶段依靠比例导引法向目标运动。因为导弹速度远大于目标速度,所以可以将目标看作朝某一方向做匀速直线运动。导弹和目标的位置关系用图3表示[8]。

图3 导弹与目标的位置关系
其中θ是初始速度方向与水平线的夹角,θt为目标运动速度与水平线的夹角,ΔR为导弹和目标之间距离,q为导弹和目标连线方向和水平线夹角。导弹和目标相对运动方程可以表示为

比例导引规律[8]:

在导弹的飞行过程中,受导弹飞行速度和弹体情况的影响,即角速度满足:

3.2 导弹命中概率模型
由于误差的存在,目标的可能位置是一个散布区域,所以运动末制导雷达对目标的捕捉概率可以看作导弹末制导雷达搜索区域覆盖目标散布区域的概率。在攻击过程中,目标与我方舰船的距离ΔR、方位q误差构成了目标定位误差,目标航向θt、航速Vt误差构成了目标运动误差。假设距离、方位、航向、航速误差其均服从正态分布为(σΔR,σq,σθt,σVt)。
将反舰导弹的末制导雷达搜索区域简化为水平面内2a×2b的矩形区域,其中b=Rzd×tanα(α为末制导雷达搜索扇面角,Rzd为自导距离)。采用文献[9]中误差椭圆合成的方法,目标散布区域近似为一个椭圆。椭圆长轴在导弹攻击方向上的概率偏差为Em[9]。
在前置点攻击方式下,搜索区域与目标散布椭圆的中心为同一点[10],如图4所示。

图4 误差椭圆与末制导雷达搜索区域关系图
正态分布事件在一定区域内的概率可以由拉普拉斯定理进行计算[11],所以其命中概率为
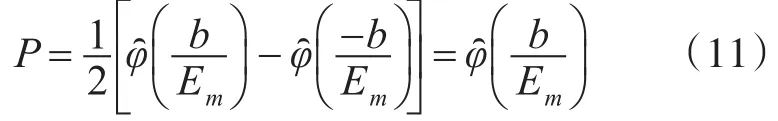
3.3 算例分析
在仿真时,输入导弹和目标各自的初始位置、速度和发射角度,根据3.1中的式(8)~(10)建立导弹在自控飞行阶段的Simulink模型进行仿真,得到自控终点的弹目状态信息,代入3.2中的命中概率模型进行计算得出导弹对目标的命中概率。算例仿真的初始值如表1所示。

表1 算例仿真开始时的初始值
在表1条件下,改变导弹的发射角度和弹目距离,得到命中概率随导弹发射角度与弹目连线夹角和弹目距离变化的变化情况,如图5所示。
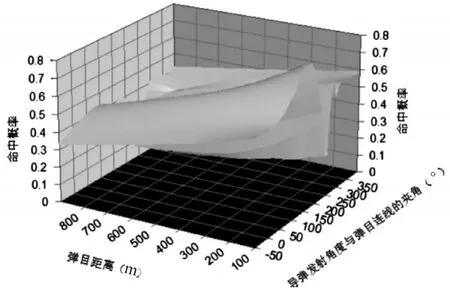
图5 命中率与发射角度的关系
从图5中可以看出,导弹命中率受发射角度的变化影响较大。当导弹在自控终点时的飞行角度与此时弹目视线角接近时,命中率高;反之则低。当固定导弹发射角度,改变目标位置使弹目距离线性增加进行实验,随着弹目距离的增加,雷达搜索区域不能够对目标散布区域进行有效覆盖,所以导弹的命中率在不断地下降。
4 舰对舰攻击分配算法
其整个分配算法过程如图6所示,当获得导弹和目标的初始位置和发射、航行角度等状态信息后,代入命中概率模型得出弹目间命中概率矩阵;然后采用分配算法依据命中概率矩阵计算分配结果,在每次分配结束后,计算此时导弹的位置、发射方向和剩余目标的位置与运动方向等弹目状态信息,进行下一轮分配。

图6 动态求解分配结果流程图
武器目标分配问题是一个NP完全问题,用传统算法(如枚举法、分支定界法)求解不现实[4]。蚁群算法是一种智能优化算法,具有分布式、快速收敛、易于与其他算法相结合等优点,被广泛用于组合优化问题求解。
蚁群算法中最重要的两部分为配对的选择规则和信息素更新规则。
1)配对的选择规则:按照随机方式排列导弹,按照下面的规则计算概率
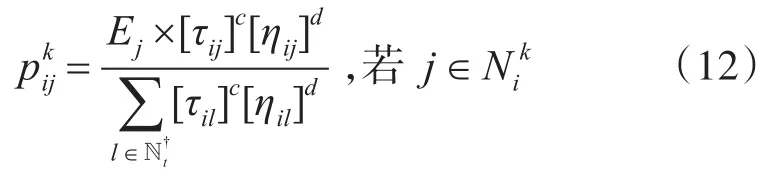
其中τij为信息素,ηij为启发式信息即导弹的命中概率,c和d分别决定信息素和启发式信息的相对影响力,代表了蚂蚁k在求解分配方案时可分配给导弹i的目标的集合。
2)信息素更新规则:将信息素矩阵分为两部分全局信息素τglobal和局部信息素τlobal,其中τglobal用于每次循环迭代前的初始信息素;τlobal为在每次迭代中的信息素。全局信息素的更新规则如下:
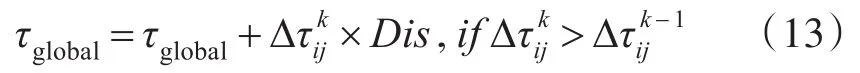
局部信息素的更新规则如下:
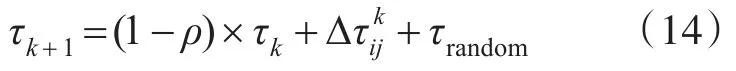
其中ρ∈(0,1)表示信息素的挥发程度;τrandom为随机概率矩阵,但对应分配对(i,j)处为0;表示蚂蚁k在分配中的信息素增量。
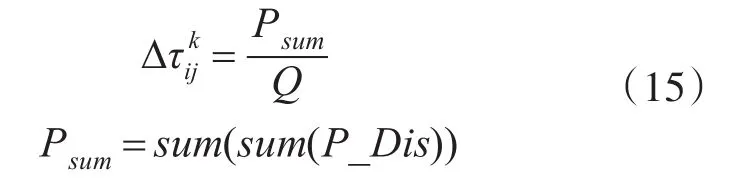
其中Q为常数,来控制算法收敛速度;P_Dis是蚂蚁k在分配过程中得到的与分配矩阵Dis相对应的概率矩阵。其中利用蚁群算法分配部分伪代码如表2所示。

表2 算法伪代码
5 仿真与验证
假定存在5个舰船,5个目标,每个目标的价值为1。在两个区域内分别随机产生5个点,作为导弹和目标的初始位置,并生成导弹的发射方向和目标的运动方向,如图7所示。

图7 弹目初始状态
利用第3节中建立的模型对命中概率进行计算,得到表3。
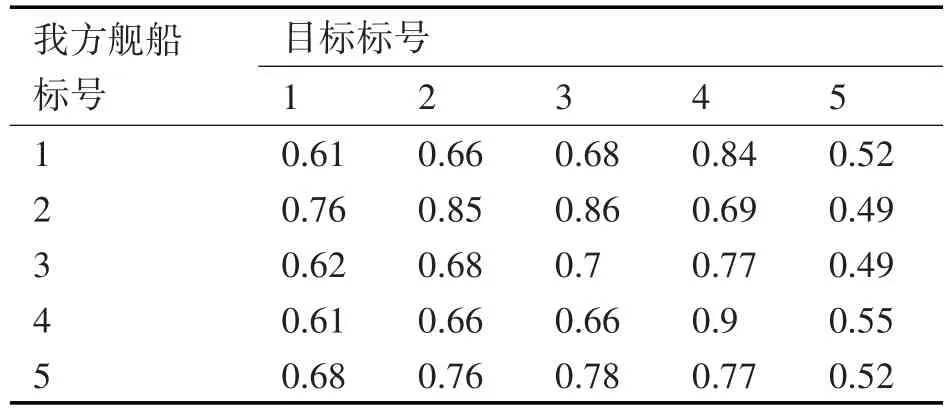
表3 第一轮时命中概率表
利用蚁群算法进行一轮分配仿真时主要参数设定:一轮迭代蚂蚁数ant_max=30、最大循环次数Nc_max=50,α=1,β=5,信息素挥发速率ρ=0.9、Q=10,命中率阈值Pa=0.65。当每艘舰只发射一枚导弹,每个目标只受一枚导弹攻击时,其分配结果如图8所示,其中黑点所对应的是分配对。

图8 一轮分配结果
当敌方舰船打击我方时进行攻击目标分配。假设求解命中概率时,不考虑导弹在自控阶段的轨迹约束,只考虑末制导雷达捕捉概率时,其他条件与本文保持一致。同时我方舰船也以航向角60°运动,求得敌对我的命中概率矩阵如表4所示。
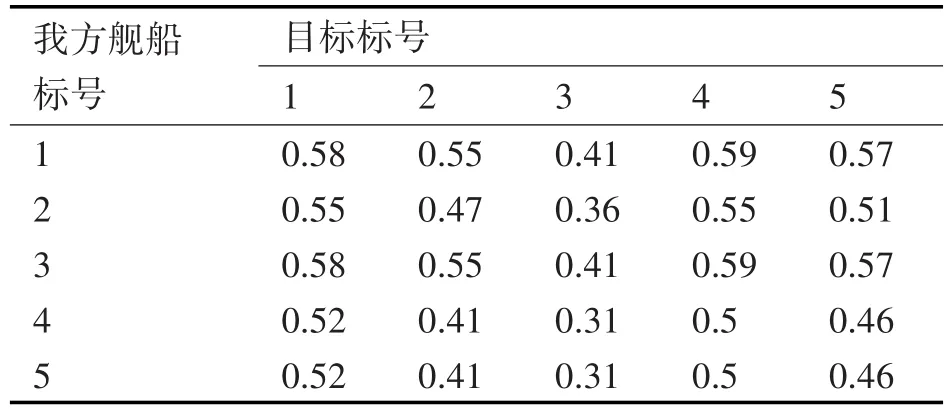
表4 命中概率表(不考虑自控段轨迹约束)
通过对比,可以看出采用不加轨迹约束的命中概率模型所产生的命中概率要低,其单轮分配的命中率和明显要小。改变弹目初始状态,进行20次动态分配实验(双方分别采用加入轨迹约束和不加轨迹约束的命中概率模型)。在每一次实验结束后,计算其平均命中概率和,其结果如图9所示。
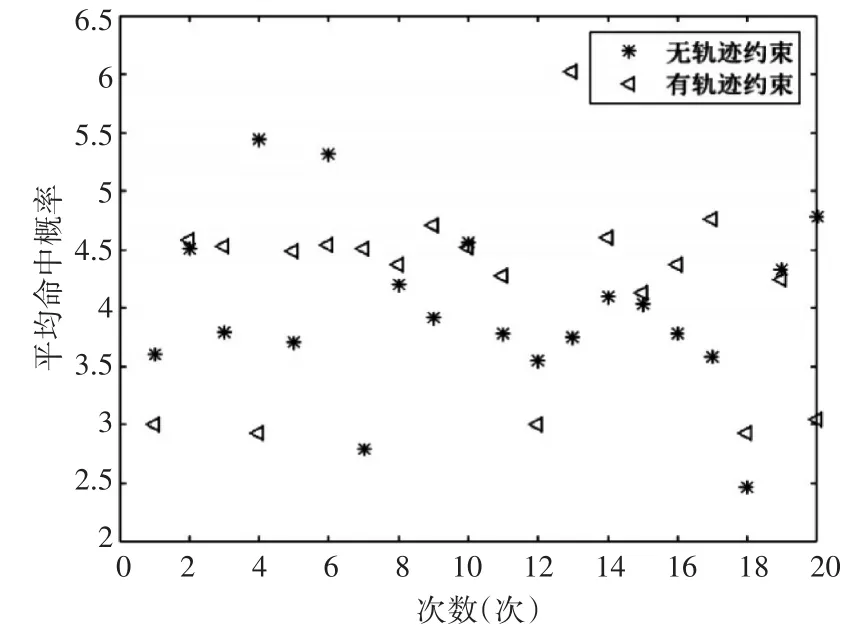
图9 20次实验两种分配结果对比
从图9中可以看出,基于有轨迹约束的命中概率模型的平均命中概率和大部分比基于无轨迹约束的命中概率模型要高,其对目标的毁伤概率也就更高,作战效果更好。在多次分配的情况下,分配方案会随着目标数量和位置的变化而改变。当敌我舰船的位置等状态信息发生变化时,导弹对目标的命中率也会发生变化,由此导致弹目间的分配方案也会发生改变。因此战斗前依靠仿真结果,可以依靠分配方案预估我方的攻击结果,进而可以指导我方调整舰艇编队的阵型,提高攻击目标的命中率,使我方占有更大的优势。
6 结语
文章首先建立目标分配的数学模型,然后依据在飞行过程中的运动特性,建立带轨迹约束的命中概率模型,在此基础上利用改进蚁群算法求解分配策略,并进行了一轮分配、多轮分配的仿真实验。仿真结果表明,由此得到的分配结果合理实用,相比其他方法在分配上具有优势,可以为安排战斗策略提供参考。在接下来的研究中将进一步对命中概率模型和分配算法进行改进。

