基于空间非迭代Oseen格式的时间解耦局部并行方法

张 蕊 张 翀 李 剑*

1(陕西科技大学文理学院 陕西 西安 710021)2(宝鸡文理学院陕西省灾害监测与机理模拟重点实验室 陕西 宝鸡 721013)

0 引 言

Navier-Stokes方程是描述水、大气和其他流体运动的一般方程，是粘性不可压缩流体的经典模型。而Navier-Stokes/Navier-Stokes耦合方程[1-2]是两个Navier-Stokes方程在接口界面上通过耦合条件得到的复杂方程组，主要出现在气象学和海洋学等理论研究中。复杂的自然现象不仅仅是单一的Navier-Stokes方程，因此耦合问题相关方法的研究也是必不可少的。

目前，Navier-Stokes/Navier-Stokes耦合问题的串行求解方法已有很多。例如：Connors等[3]运用传统方法解决Navier-Stokes/Navier-Stokes耦合问题，并且分析了其稳定性与收敛性，在很大程度上保证了计算的准确性；文献[5]通过运用牛顿格式的解耦方法分析流体耦合问题的稳定性与误差估计，证明该解耦方法不仅无条件稳定而且长时间稳定；文献[6]提出空间非迭代Oseen格式的欧拉时间推进方法，通过空间一步校正非线性项，仅用三层时间推进求解耦合问题。

耦合问题的数值模拟面临两大困难：较大的数据存储空间和较长的计算时间。因此，需要借助并行计算技术实现快速求解。目前，国内外大批的科研人员与学者致力于单一Navier-Stokes方程并行有限元方法的研究，并取得了相关成果[7-13]。其中，单位划分与自适应网格相结合的统一分区并行方法被称作是一种灵活可控的区域分解方法[14-15]。Zheng等[7]提出了一种求解定常Navier-Stokes方程的局部并行有限元算法，通过划分粗细网格，结合粗网格上的全局解与细网格上的局部解，最终得到有限元数值解。文献[8]设计了两种求解非定常Navier-Stokes方程的并行数值算法，一种是将Picard迭代法和区域分解算法相结合的并行Oseen线性化方法，另一种是基于两重网格离散方法的有限元并行算法。而文献[12]通过结合有限元方法与统一划分方法，提出了一种求解时间依赖对流扩散方程的局部并行方法。

相比于单一Navier-Stokes方程的并行方法，耦合方程的并行有限元方法研究较少。因此，根据空间非迭代Oseen格式的欧拉时间推进方法与单元划分的局部并行方法[7]，提出Navier-Stokes/Navier-Stokes耦合方程空间非迭代时间解耦的局部并行方法。在FreeFem++软件的MPI并行功能[16]下，通过解耦复杂区域、处理边界条件以及划分并行区域，最终得到耦合模型的数值解。最后通过数值实验验证欧拉时间推进方法的精确性以及时间解耦局部并行方法的高效性。

1 预备知识

1.1 Navier-Stokes/Navier-Stokes耦合方程

本文主要考虑的Navier-Stokes/Navier-Stokes耦合方程为：

ui=0 onΓi=∂ΩiI

(6)

式中：耦合区域Ω=Ω1∪Ω2由子区域Ω1、Ω2组成，其中Ωi⊂Rd,d=2，3，ni为单位外法向量,i=1,2;I为接口界面；粘性系数νi>0,i=1,2；κ为给定的参数；Δ表示拉普拉斯算子；速度ui:Ωi×[0,T]→Rd，其中T表示时间；压力pi:Ωi×[0,T]→R；体积力fi:[0,T]→[H1(Ωi)]d。耦合区域如图1所示。

图1 耦合区域图

为了解决耦合问题，提出如下两个空间：

Xi={vi∈[H1(Ωi)]d:vi=0 onΓi;vi·ni=0 onI}

式(1)与式(4)的两端分别乘以vi∈Xi与qi∈Mi，运用格林公式，得到式(1)-式(6)的变分形式，求解(ui,pi)∈Xi×Mi，使得(vi,qi)∈Xi×Mi，满足：

b(ui,ui,vi)-d(vi,pi)=(fi,vi)

(7)

d(ui,qi)=0

(8)

双线性型a(·,·)与d(·,·)定义在Xi×Xi与Xi×Mi上：

并且满足连续性和inf-sup条件：

式中：C是常数；β>0。

三线性项b(·,·,·)定义在Xi×Xi×Xi上：

并且满足如下反对称性：

b(ui,vi,wi)=-b(ui,wi,vi)ui,vi,wi∈Xi

以及连续性：

一个实际的模型包括很多复杂项，本文仅讨论耦合模型的算法问题。

1.2 欧拉时间推进方法

空间非迭代Oseen格式的欧拉时间推进方法主要运用Oseen格式一步校正非线性项，而耦合边界式(2)则用如下的标准几何平均跳跃[3]进行处理：

式中：Span表示扩张的空间。

并且满足性质：

式中：c表示常数。

下面介绍空间非迭代Oseen格式的欧拉时间推进算法。

算法1空间非迭代的欧拉时间推进算法

(9)

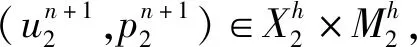
(10)

2 时间解耦的局部并行方法

基于空间非迭代欧拉时间推进方法，给出Navier-Stokes/Navier-Stokes耦合方程时间解耦的局部并行方法。

首先，复杂区域Ω解耦为两个单一子区域Ωi，解耦区域如图2所示。因此，区域Ω内耦合方程的求解转换为两个子区域Ωi内单一方程的求解。

图2 区域解耦图

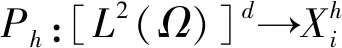
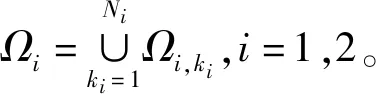
为了方便，定义:

(11)

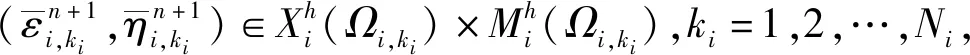
根据耦合区域Ω的边界条件式(2)、式(3)、式(6)，设置并行区域Ωi,k的不同边界条件：

(1) 若并行区域为耦合边界，设置式(2)为并行区域的边界条件。

(2) 若并行区域为人工边界，则由如下的第一类边界条件代替：

(12)

(3) 若并行区域为混合边界，结合耦合边界式(2)与人工边界式(12)进行并行计算。

因此，通过将耦合区域Ω上的方程转换为并行区域Ωi,ki上方程的求解，根据并行区域边界条件的设置，本文提出时间解耦的局部并行算法，从而获得Navier-Stokes/Navier-Stokes耦合方程的近似解。

算法2时间解耦的局部并行方法

步骤3得到耦合方程的近似解：

3 数值实验

为了验证时间解耦局部并行方法的准确性，提出如下三个数值实验。所有实验使用的计算机CPU型号为Inter酷睿i7-8700 3.20 GHz，8 GB内存。算法1由软件FREEFEM++完成，算法2的实现以FREEFEM++的MPI为平台，网格采用三角形单元，有限元为P1b-P1。耦合方程的精确解详见文献[3,5]。

假设区域Ω1=[0,1]×[0,1],Ω2=[0,1]×[-1,0]外法向量n1=[0,-1]T,n2=[0,1]T，边界I是x轴上0到1的位置，给定参数ν1=0.5,ν2=0.05,α=1,κ=100,T=1。并且速度ui与压力pi的误差表示为：

1) 给出串行方法的误差与时间结果。固定时间步长Δt=0.01，改变子区域Ωi网格剖分的尺寸h，运用算法1求解Navier-Stokes/Navier-Stokes耦合方程，观察数值解的误差精度与求解时间，结果如表1-表2所示。

表1 欧拉时间推进方法的速度误差结果

表2 欧拉时间推进方法的压力误差和时间结果

表1-表2验证了Navier-Stokes/Navier-Stokes耦合方程的数值解中，速度解和压力解的收敛阶均达到了一阶，但随着网格剖分的增大，运行时间越来越长。

2) 为了说明空间非迭代Oseen格式的优越性，比较空间非迭代的Oseen格式与Oseen迭代格式、牛顿迭代格式、简单迭代格式四种格式的求解时间。固定子区域Ωi的网格剖分h=1/16，时间步长Δt=0.01得到时间对比结果，如表3所示。

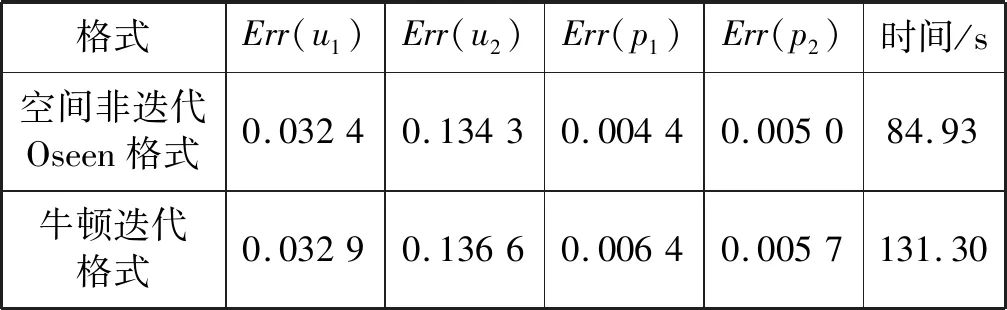
表3 四种格式的误差和时间对比结果

续表3

从表3可以看出，在误差精度方面，四种格式相差不大，但从运行时间来看，我们所选择的空间非迭代Oseen格式的求解时间相对最短。

3) 为了评估时间解耦局部并行方法的高效性，分别运用算法1与算法2来计算耦合方程的有限元近似解，从而比较两种方法的求解时间。

首先，分别给定网格剖分h=1/12,1/48，改变时间步长Δt=0.1,0.05,0.025,0.012 5，得到时间结果如表4-表5所示。

表5 网格剖分h=1/48的时间结果

通过表4-表5可以发现：与空间非迭代Oseen格式的欧拉推进方法相比，时间解耦局部并行算法节省的时间均在45%以上。这说明当网格剖分h不变时，改变时间步长Δt，并行算法的求解时间相对较短，即收敛速度较快。

然后，分别固定时间步长Δt=0.1,0.01，改变网格剖分h=1/12,1/24,1/48，得到时间结果如表6-表7所示。

表6 时间步长Δt=0.1的时间对比结果

表7 网格剖分Δt=0.01的时间对比结果

从表6-表7可以看出：与欧拉时间推进方法相比，当给定时间步长Δt时，时间解耦的局部并行方法至少节省38%以上的时间，而最大节省的时间达到70%。即改变区域网格剖分h，时间解耦局部并行方法的运行时间相对较短。

4 结 语

基于空间非迭代Oseen格式的欧拉时间推进方法，提出了求解Navier-Stokes/Navier-Stokes耦合方程时间解耦的局部并行方法。通过对复杂区域进行解耦，将耦合方程转换为并行区域上的单一方程进行求解。改变子区域网格剖分的尺寸，从而确定并行区域的大小，在多个并行区域上同时计算。可以发现：不论是改变网格剖分的尺寸，还是时间步长的大小，时间解耦的局部并行算法在取得与原有串行算法相同精度的情况下，均有相对较快的收敛速度，即减少了Navier-Stokes/Navier-Stokes耦合方程的求解时间，在一定程度上体现了并行算法的高效性。