考虑桩径效应的桥梁结构地震风险分析

万华平，卫志成，苏 雷，任伟新

(1.浙江大学 建筑工程学院，杭州 310058；2.合肥工业大学 土木与水利工程学院，合肥 230009；3.青岛理工大学 土木工程学院，山东 青岛 266033；4.深圳大学 土木与交通工程学院，广东 深圳 518060)

桥梁结构地震风险分析是分析地震作用下，桥梁结构满足各种预定目标和性能的能力，可较全面地反映桥梁结构的抗震性能。通过桥梁结构地震风险分析手段可有效评估桥梁结构的抗震性能，据此可有效指导桥梁结构的抗震设防，减小地震灾害带来的损失。

在新一代基于性能的地震工程理论框架里[1]，地震风险分析包括概率地震危险性分析、概率地震需求分析、概率抗震能力分析和概率损失分析四个部分。概率地震危险性分析与工程场地有关，概率地震需求分析与地震动强度参数和工程需求参数有关，概率抗震能力分析与结构损伤状态有关，概率损伤分析与震后损失有关。

Lupoi等[2]评估了简支梁桥和连续梁桥的地震风险。Padgett等[3]评估了南卡罗来纳州区域的桥梁地震风险。钟剑等[4]研究了斜拉桥的地震风险。于晓辉[5]和吕大刚等[6]推导了考虑能力不确定性的地震风险分析解析解。以上关于桥梁结构地震风险分析的有限元建模部分，采用土弹簧来模拟桩-土相互作用，未考虑桩径效应以及桩-土界面耦合效应(剪切方向)对桥梁结构地震风险的影响。

桩径效应指桩的直径(即桩所占的空间体积)对桩-土相互作用的影响。国外学者Dunnavant等[7]、Aissa等[8]研究发现桩径效应对p-y曲线(即反力-变形关系)有明显影响。张海洋等[9]研究了桩径效应对海上风机结构桩基础p-y曲线的影响。Elgamal等[10]和Feng等[11]研究了考虑桩径效应的桥梁结构的地震响应。以上研究工作表明，桩径效应对桩-土相互作用会产生影响，应在桥梁结构地震反应分析中加以考虑。

目前国内外桩径效应的研究主要是关于桩径效应对桩p-y曲线的影响，而关于桩径效应对桥梁结构地震风险的影响的研究工作很少。本文以一座三跨连续梁桥为例，研究桩径效应对桥梁地震风险的影响。建立了桥梁结构的三维模型，同时考虑桩所占的空间体积和桩-土间的摩擦接触。采用OpenSees有限元软件模拟桥梁结构，其中刚性连接单元用于模拟桩径效应，零长度单元用于模拟桩与土的摩擦接触。增量动力分析方法[12]用来对桥梁结构进行动力时程分析，探究了桥梁结构的地震风险。同时建立墩底固结模型和未考虑桩径效应的模型，对比分析桩径效应对桥梁结构地震风险分析的影响。

1 地震风险分析方法

地震风险是指在规定时间内和区域内，地震灾害对社会和经济的危害大小。地震风险与场地地震危险性、结构地震易损性以及地震造成的损失有关。地震危险性是指区域内不同强度地震发生的概率；地震易损性分析是指结构发生地震破坏的概率，包括概率地震需求分析和概率抗震能力分析两部分；地震损失是指地震带来的直接、间接经济损失和人员伤亡损失。

工程抗震领域的地震风险分析一般不考虑地震发生时所造成的损失，因此结构地震风险分析通常涉及地震危险性和结构地震易损性。结构地震风险可以写出如下形式：

(1)

式中:HLS为地震风险函数;F(x)为地震易损性函数;HIM(x)为地震危险性函数;x为地震动强度参数。式(1)表示为结构超越某一极限状态的年平均发生概率。

1.1 地震易损性分析理论

结构的地震易损性是指结构在受到某种强度的地震作用时，达到或超过预定极限状态的条件失效概率。地震易损性从概率的角度出发，评估结构的抗震性能，能很好地考虑结构不确定性的影响。

对于地震荷载作用，结构的失效概率(pf)与结构能力(C)和结构需求(D)有关。在某一强度地震动作用下，结构需求超越结构能力导致结构失效的概率可表达为：

pf=[D>C|IM]

(2)

式(2)表明地震易损性分析包括概率地震需求分析和概率抗震能力分析两部分。

概率地震需求模型定义了地震动强度与结构地震需求之间的关系。Cornell等[13]认为，结构的地震需求中位数(Sd)与地震动强度参数(Sa或PGA)符合以下指数关系：

Sd=aIMb

(3)

式中:IM表示地震强度参数;a和b是指数模型的系数。

对等式(3)两边同时取对数，则可以被改写为：

ln(Sd)=ln(a)+bln(IM)

(4)

概率地震需求模型的表达式为：

HD(d|x)=P[D≥d|IM=x]=

(5)

式中:HD(d|x)表示概率地震需求函数，d表示某种损伤状态的极限值，Φ[·]表示标准正态分布函数，βd|IM表示结构地震需求的对数标准差。

结构概率抗震能力模型表示在给定地震需求水平下，结构达到或超过不同破坏等级的条件概率，其表达式为：

(6)

式中:HC(d)表示概率抗震能力函数;Sc表示结构抗震能力的中位数;βc表示结构抗震能力的对数标准差。

根据式(2)的计算理论，结合概率地震需求模型与概率抗震能力模型，得到地震易损性函数如下：

(7)

1.2 地震易损性分析步骤

结构地震易损性的分析方法主要有经验方法和理论方法。经验方法通常需要专家学者根据大量的实际震害数据和经验，得到破坏概率矩阵，然后拟合出经验易损性曲线。然而经验易损性曲线的使用受到场地条件、地震环境、桥梁情况等条件限制，难以推广。相对于经验方法，理论方法由于不受这些条件限制，因而得到广泛研究。增量动力分析方法是一种动力非线性分析方法，它能清楚地展现桥梁结构在地震作用下破坏的全过程，常用来结构地震易损性分析。基于增量动力分析方法的桥梁结构地震易损性分析如图1所示，主要包含以下几步：

图1 地震易损性分析流程

步骤1建立桥梁结构的非线性有限元模型；

步骤2选择合适的地震动记录，并对选择的地震动进行调幅，得到一系列不同强度的地震动记录；

步骤3将调幅后的地震动记录输入到有限元模型，得到对应的地震响应；

步骤4根据计算得到的响应数据，通过回归分析建立概率地震需求模型；

步骤5选择桥梁结构的损伤指标，定义相应的极限状态，建立概率抗震能力模型；

步骤6计算不同强度地震动作用下，桥梁结构达到或超越某一极限状态的条件概率，绘制地震易损性曲线。

1.3 地震危险性分析

地震危险性是指某一场地在未来一段时间内某一地震动强度发生的年超越概率。地震危险性可采用极值Ⅱ型分布函数表示[14]：

(8)

式中，u和k为极值Ⅱ型函数的参数。

HIM(x)可采用幂指数进行逼近[15]：

HIM(x)=k0x-k

(9)

式中，k0和k为形状参数，可利用下式计算[16]：

(10)

ln(k0)=ln[vDBE(IMDBE)k]

(11)

式中:v表示年超越概率;DBE表示中震情况;MCE表示大震情况，vDBE=1/475=0.002 1，vMCE=1/2 475=0.000 4；IMDBE，IMMCE为DBE和MCE对应的地震动强度。

将式(7)和式(9)代入式(1)中，可以得到地震风险的解析表达式：

(12)

2 桥梁结构与有限元模拟

2.1 桥梁结构介绍

选用的桥梁为三跨连续梁桥，跨径组合为3×20 m。上部结构为预应力混凝土连续箱梁，为三箱单室结构，采用C50混凝土。桥墩为实心圆形墩，直径为1.3 m，墩高7.5 m，采用C30混凝土。桥梁的桩基础采用钻孔灌注桩，桩直径为1.5 m。桥型总体布置如图2所示。

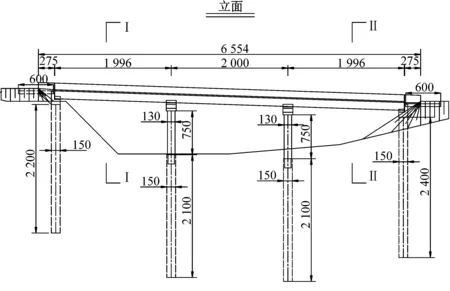
图2 桥型布置图

2.2 墩柱和上部结构模拟

在OpenSees有限元分析软件中建立该连续梁桥的非线性有限元模型。桥梁的箱梁采用纤维截面的非线性梁柱单元模拟。为了模拟三箱单室的主梁，建立三条平行线，三条平行线在横桥方向的位置分别是三个箱室的中心线。桥梁墩柱同样采用纤维截面的非线性梁柱单元模拟，图3(a)为墩柱的纤维截面。

箱梁结构和墩柱结构的混凝土都选用OpenSees材料库中的Concrete01材料，其本构关系采用了Kent-Scott-Park模型。保护层混凝土的本构关系如图3(b)所示，核心混凝土的本构关系如图3(c)所示。

墩柱和箱梁结构的钢筋采用OpenSees材料库中的Steel02材料，其本构关系采用Giuffre-Menegotto-Pinto模型，如图3(d)所示。箱梁结构中的预应力钢绞线也采用Steel02材料，其本构关系采用带有初始应力的Giuffre-Menegotto-Pinto模型，如图3(e)所示。

图3 纤维截面和材料本构关系

2.3 桩-土连接模拟

桩-土相互作用是非常复杂的动力相互作用问题，其模拟精度关系到地震分析结果的准确性。在模拟桩-土接触时，应同时考虑到桩径效应和桩与土的滑动摩擦。

参考Elgamal等[10]提出的刚性连接模拟方法，本文采用刚性连接单元模拟桩径效应。刚性连接单元可用来考虑桩径效应，同时可避免桩-土界面滑动导致阻尼力过大问题。为模拟桩-土的滑动摩擦，在刚性连接单元外添加相应的零长度单元，用于近似模拟桩-土摩擦滑动机理[17]。如图4所示，桩四周设置若干个垂直于轴线方向的刚性连接单元，零长度单元用来连接刚性连接单元和土体单元。该模拟方法能很好地考虑桩-土接触的力学行为，有效模拟了桩直径方向的压力、桩切线方向及沿桩轴线方向的剪切力，同时考虑了桩在土体中所占的空间体积，使建立的模型更加相符实际情况。同时这种模拟方法已通过合作者所完成的桩基振动台试验得到很好的验证[18]，表明这种模拟方法能很好地模拟地震中桩-土动力相互作用。

由于零长度单元只能连接自由度相同的两个节点，而刚性连接单元与土单元的自由度不同，所以无法在两者之间直接建立零长度单元。考虑到OpenSees中的equalDOF约束可以连接不同自由度的节点，为此增加一个节点(图4中的点A)用于建立零长度单元。在A点与刚性连接单元间建立零长度单元，同时采用equalDOF约束将A点与土单元相连。零长度单元连接方式如图5所示。

图4 三维模型的桩-土连接

图5 桩-土相互作用模拟方法

图5中两个并联的零长度单元zeroLength单元和zeroLengthSection单元，其中zeroLength单元提供垂直桩轴线方向的轴力，zeroLengthSection单元提供沿桩轴线方向和桩切线方向的耦合剪切力。为模拟桩-土界面滑移，需要在两个零长度单元上定义剪切屈服力。粘土层桩-土界面剪切屈服力仅与黏聚力有关，可按下式计算：

Fcohesion=l·h·c

(13)

式中：l表示桩周长；h表示相邻桩单元中心点到中心点距离；c表示土体黏聚力。

砂土层桩-土界面剪切屈服力仅与摩擦角有关，按下式计算：

(14)

式中:σv表示竖向应力；v表示泊松比；φ表示摩擦角。

若零长度单元处于黏土层与砂土层的分界面，剪切屈服力计算需同时考虑黏聚力和摩擦角的影响。

当沿桩周方向的零长度单元个数为N时，需要将式(13)、(14)平均到N个单元，得到每个零长度单元的剪切屈服力。

建立的三维有限元模型如图6所示，共有24 097个节点，1 130个梁柱单元，20 176个非线性brickUP单元和43个四节点平面单元。

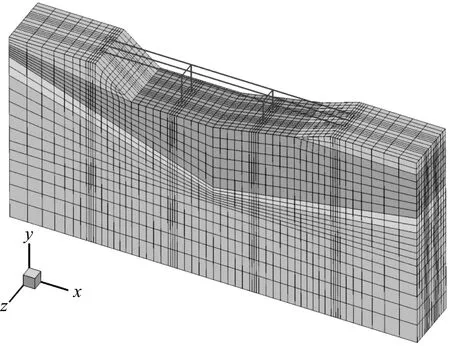
图6 桩-土-桥梁结构体系的有限元模型

3 地震风险分析

3.1 地震动参数与地震波的选取

地震动强度参数有很多种，常用的有峰值加速度PGA、峰值速度PGV、谱加速度Sa等。选取合理的地震动强度参数对于概率地震需求分析非常重要。由于我国的地震动参数区划图提供了地震动峰值加速度区划，同时获得PGA相对容易，因此本文采取峰值加速度PGA作为地震动强度参数。

根据JTG/T B02-01—2008《公路桥梁抗震设计细则》生成设计加速度反应谱，将其导入美国太平洋地震工程研究中心(PEER)的数据库中，PEER会给出与设计加速度反应谱相匹配的地震波。本文根据以下原则选择地震波：

(1)以E2地震作用下的设计加速度反应谱为目标反应谱，所选取地震波的反应谱与目标反应谱吻合度较好；

(2)所选地震波的特征周期与桥梁所处场地的固有周期尽量接近[19]；

(3)所选地震波持续时间应为结构基本周期的5倍～10倍。

从PEER导出的地震波中筛选出符合度较好的数条地震波，如图7所示。接着，对所选地震波按式(15)进行调幅，得到90条地震波。

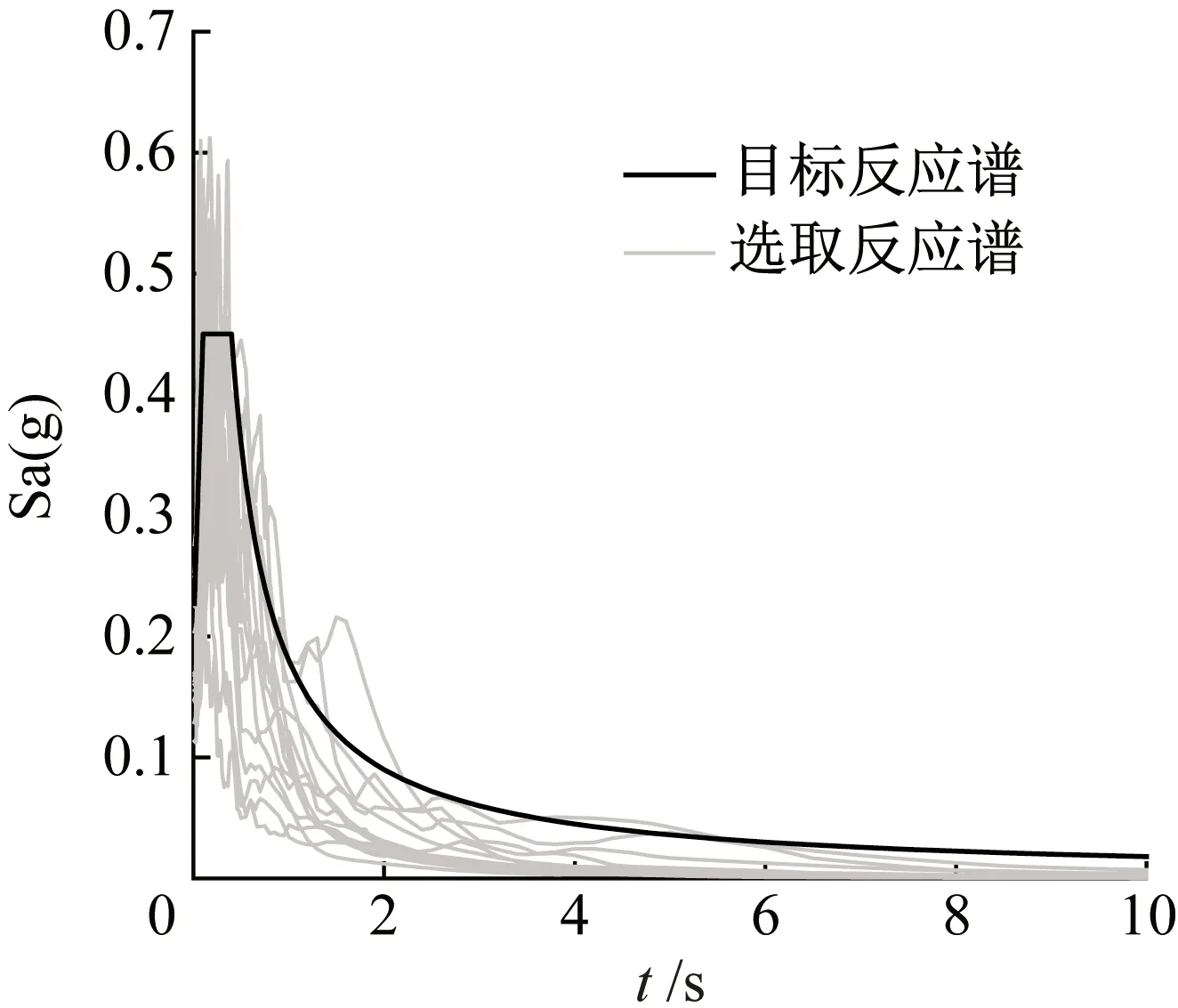
图7 地震波反应谱

(15)

地震波的调幅系数约为[1,6]，采用等步调幅方法对地震波进行调幅，并将地震波峰值加速度控制在[0.1g,1.2g]。

3.2 极限状态与损伤指标

对于梁桥，桥墩顶端的位移或桥墩延性是定义桥梁损伤水平的重要指标。桥墩顶端位移可以反映桥墩的损伤状态，而且较为容易获得。桥墩延性可以表示桥墩抵抗地震作用的能力。为此结合两者，本文采用位移延性比作为桥梁结构的损伤指标[20]。桥梁结构的地震破坏可分为五种破坏状态，可用桥墩位移延性比描述，如表1所示。

表1中，μd表示桥墩的相对位移延性比，μcy1是首次屈服的位移延性比，μcy是等效屈服位移延性比，μcy4是混凝土应变ε=0.004时的位移延性比，μcmax是最大位移延性比，如表2所示。

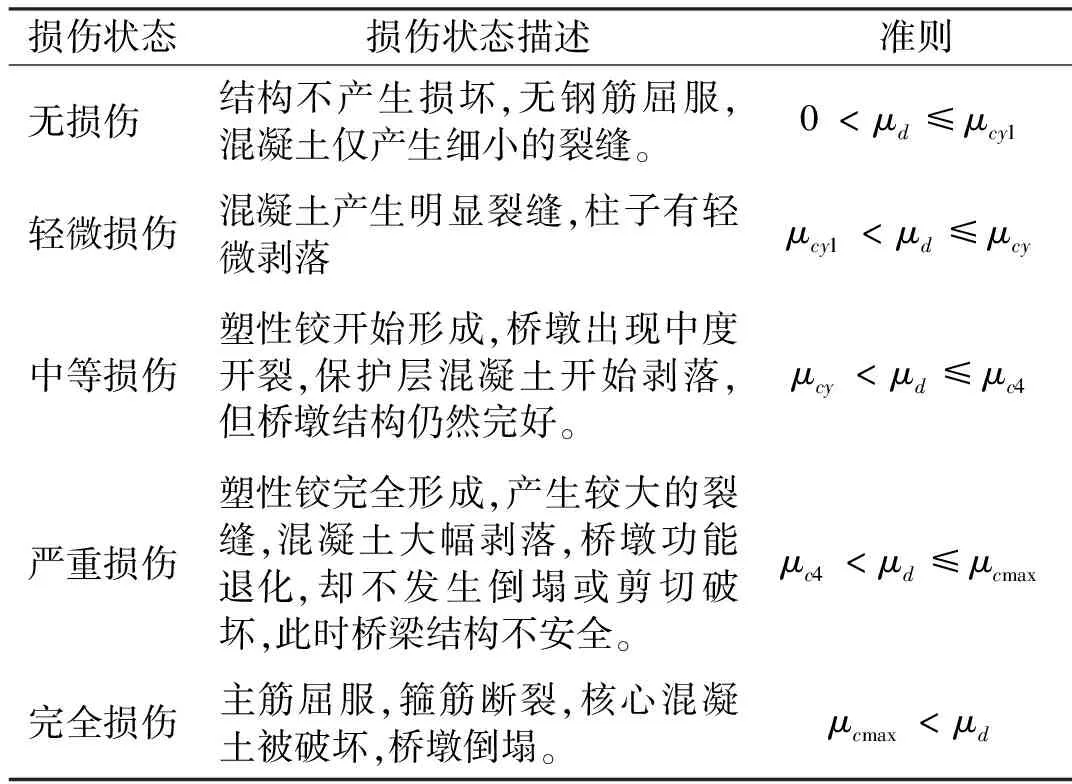
表1 桥梁损伤状态与判别指标[21]

表2 损伤指标值[21]

在确定了极限状态和损伤指标后，需要考虑结构能力的不确定性。结构能力不确定性一般使用对数标准差βc来反映，考虑到不同极限状态下的桥梁抗震能力不同，所采用的对数标准差应有所区别。较低的损伤状态(轻微损伤和中等损伤)取βc为0.246，较高的损伤状态(严重损伤和完全损伤)取βc为0.472[22]。

3.3 地震易损性曲线

为了考察桩径效应的影响，共建立了三个有限元模型，分别记为模型一、模型二和模型三。三种模型的建模方式如下：

模型一：考虑桩径效应的桩-土相互作用模型。使用刚性连接单元模拟桩径效应，使用零长度单元模拟桩-土滑动摩擦。

模型二：不考虑桩径效应的桩-土相互作用模型，在模型一的基础上去除刚性连接单元，仅用零长度单元模拟桩-土相互作用。

模型三：墩底固结模型。不考虑桩及桩-土相互作用的模拟，将桥墩底部与土体固接。

调幅后的地震波分别输入上述的三个模型，记录桥墩顶端相对位移，然后计算位移延性比。通过增量动力分析得到概率地震需求模型，结果如图8所示。

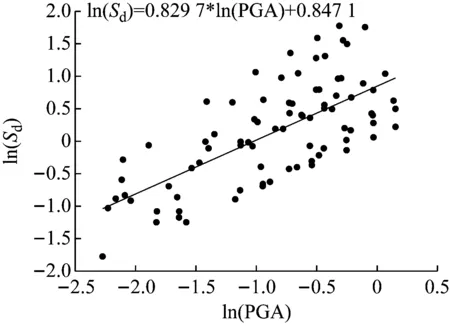
(a)模型一

根据地震易损性步骤(图1)，可得到桥梁结构的地震易损性曲线，结果如图9所示。

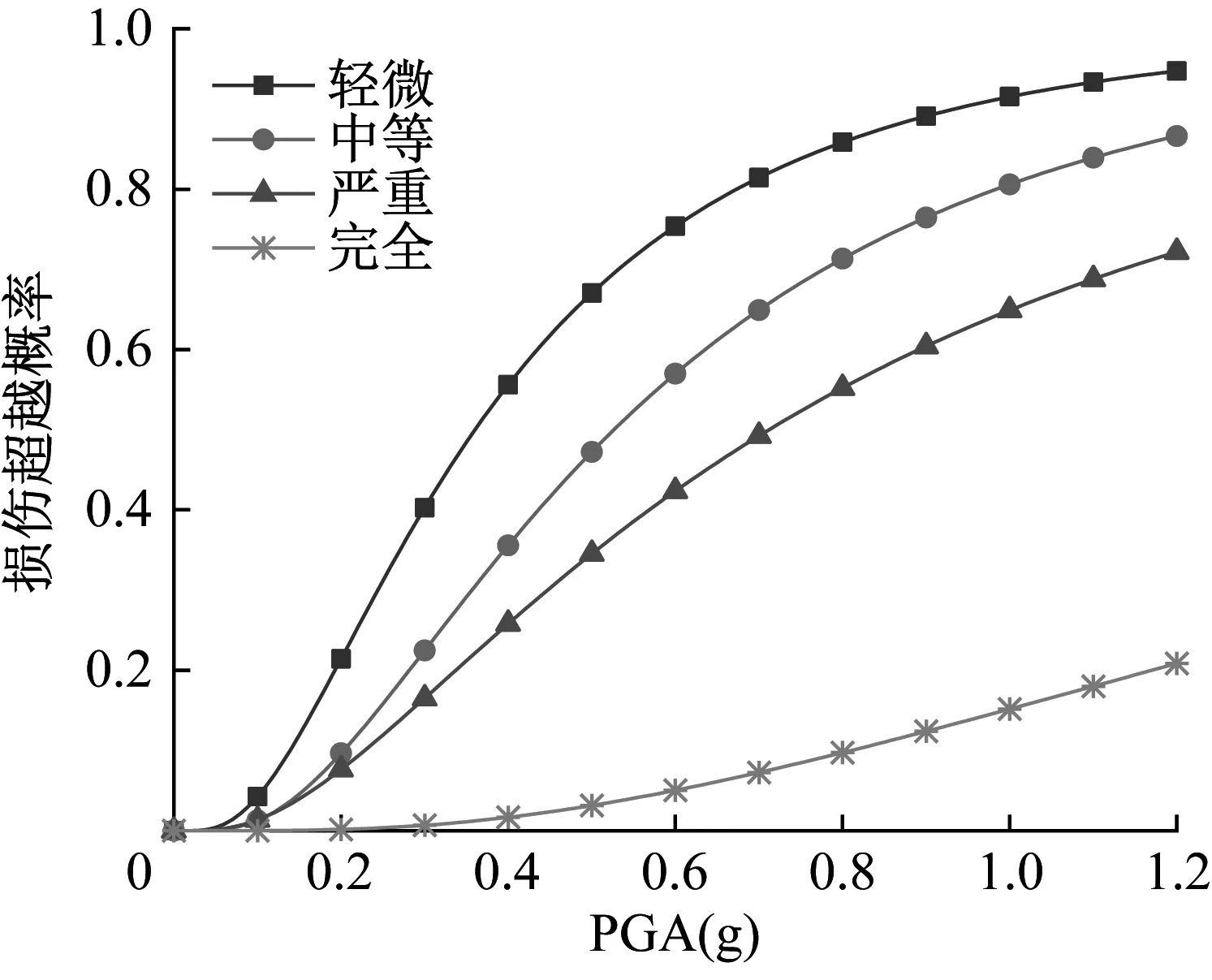
(a)模型一

由图9可知，不同损伤状态下桥梁结构的损伤概率随峰值加速度PGA的增大而增大。轻微破坏和中等破坏的地震易损性曲线间隔相对中等破坏与严重破坏、严重破坏与完全破坏间的地震易损性曲线间隔小。

为了对比三个模型的地震易损性分析结果，分别将四种不同极限状态下的桥梁地震易损性曲线进行对比，结果如图10所示。

由图10可以看出，在同一种损伤状态下，随着PGA的增大，三个模型的损伤概率增长趋势相似。考虑桩径效应的模型对应的损伤概率低于不考虑桩径效应的模型，墩底固结模型对应的损伤概率最低。这是因为不考虑桩径效应的桩-土相互作用模型桥墩顶端峰值位移最大，更容易发生损伤；而墩底固结模型的桥墩顶端峰值位移最小，延性能力更高。

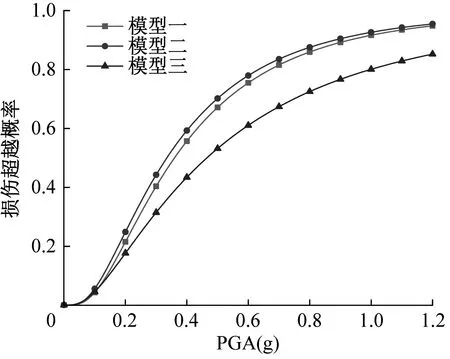
(a)轻微损伤

3.4 地震风险分析结果

桥梁的地震风险分析包括地震危险性分析和桥梁地震易损性分析。地震易损性分析结果已在上一节给出，因此只需要再进行地震危险性分析。

在地震危险性分析时，需要求出地震危险性函数，该函数与形状参数k及k0有关，因此需要根据式(10)、(11)计算出两个形状参数的值。根据中国地震动参数区划图，可以得到IMDBE=0.2 g，IMMCE=0.38 g，从而计算得到：k=2.583 5，k0=3.284 2×10-5。

将k，k0代入式(12)计算得出桥梁在不同极限状态的地震风险，结果如图11所示。

图11展示了三个模型在四种损伤状态下的地震风险曲线。可以看出，随着位移延性比的增加，桥梁结构的地震风险明显减小。因此提高桥墩的位移延性能力，可以减少桥梁结构的遭受地震作用破坏的风险。随着位移延性比的增加，三个模型的地震风险降低趋势相似。与墩底固结模型相比，考虑桩-土相互作用的模型对应的地震风险更高。对于桩-土相互作用的模型，考虑桩径效应时桥梁结构的地震风险小于不考虑桩径效应的地震风险。

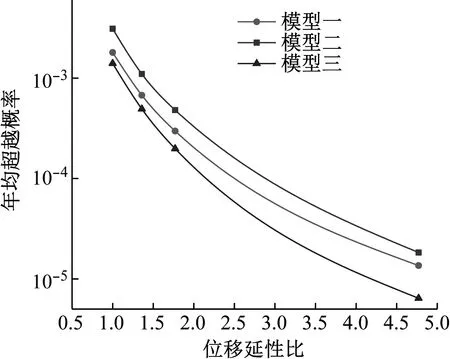
图11 不同损伤状态的地震风险曲线

4 结 论

本文建立了考虑桩径效应的桩-土-桥梁结构体系的有限元模型，采用刚性连接单元模拟桩的几何尺寸，采用零长度单元模拟桩-土间的滑动摩擦。该建模方式在模拟桩-土相互作用同时考虑桩径效应的影响。同时建立不考虑桩径效应的桩-土相互作用模型和墩底固结模型两个模型，用于对比分析。基于增量动力分析方法计算桥梁结构的地震易损性曲线和地震风险曲线。分析结果表明，与墩底固结模型相比，考虑桩-土相互作用时，桥梁结构的地震易损性和地震风险更大。对于桩-土相互作用的模型，不考虑桩径效应会增加桥梁结构的地震风险。因此，桥梁结构抗震分析应同时考虑桩-土相互作用和桩径效应的影响。