软土地区基坑侧位移变形预警及预测

王 娟，王兴科

(陕西铁路工程职业技术学院，陕西 渭南 714000)

1 研究背景

近年来，市政交通快速发展， 地铁基坑工程日益增加。 受环境条件限制， 基坑位置多位于建筑密集区， 为保证施工及周边既有建筑物安全， 基坑施工过程的侧位移控制尤为重要[1]。 目前， 国内外许多学者进行了基坑变形预警方面的研究， 在国外， 如， Lambe[2]以基坑变形数据为基础， 通过变形预测实现了基坑变形预警研究； Goldberg等[3]通过多基坑变形成果及地质环境条件统计， 构建了基坑变形预警模型， 为现场施工提供了一定指导； 而国内在预警研究方面， 如张志会等[4]在利用尖点突变理论进行基坑稳定性评价基础上， 利用速率比值法进行预警状态划分， 有效保障了基坑施工过程的信息化施工； 郑帅等[5]利用支持向量机实现了基坑变形预测， 并将预测结果与变形警戒值对比， 划分出了预警等级， 实现了基坑变形的超前预警； 王乾坤等[6]利用神经网络实现了基坑预警源的多元信息融合， 合理预测了警情位置及类型。 上述研究均为基坑预警提供了相应思路， 但其预警指标相对较为单一， 也未涉及去趋势波动分析方法的应用研究， 进而仍需进一步拓展研究基坑预测模型。 同时， 在基坑变形预测方面， 郭健等[7]利用小波变换和Elman神经网络构建了基坑变形预测模型， 所得结果具有较高的预测精度； 郭庆军等[8]利用有限元分析了基坑变形发展趋势， 为其施工提供了指导； 谢洋洋等[9]在混沌理论相空间重构基础上， 利用支持向量机实现了基坑变形预测， 其结果具有较强的稳定性。

上述研究在基坑变形预测方面取得了一定成果，但也存在一定不足，如有限元分析忽略了基坑周边土体的非均一性，也未对模型参数进行优化预测研究。因此，为实现基坑侧位移变形特性的综合研究，笔者以安元西路站为工程背景，分别构建了基坑侧位移预警模型和预测模型，两者对比佐证，以保证分析结果的准确性。

2 基本原理

本文研究主要包含两部分内容，即变形预警模型和预测模型的构建。其中，预警模型以多重分形去趋势波动分析方法(Multi-Fractal Detrended Fluctuation Analysis， MF-DFA)为基础，构建出预警判别指标，再利用Spearman秩次检验实现判别指标的变化趋势判断，进而完成预警等级划分；变形预测模型则以脊波神经网络为基础，通过粗集理论和试错法优化模型参数，构建出优化变形预测模型，以保证预测精度。各方法的应用原理分述如下。

2.1 预警等级评价模型的构建

MF-DFA分析是一种多重非均匀分形方法，能准确揭示基坑变形过程中的发展趋势信号，具有较多优点，如：通过改变波动函数的阶次，能得到评价序列的多重分形特征；在设定波动函数阶次前提下，能合理评价序列的发展趋势。同时，鉴于基坑变形具有非连续多尺度特征，进而利用MF-DFA分析实现其侧位移预警具有较强的可行性[10]。

根据MF-DFA分析的基本原理，将其分析过程详述如下：

(1)将基坑变形序列设定为{xi}(i=1，2，…，N)，求解其累计离差序列yi,即

(1)

式中：N为序列长度；x′为变形平均值。

(2)对累计离差序列yi进行子区间划分，将子区间长度设定为s，共计得到子区间个数Ns=N/s(非整数时取整数)；同时，为充分发挥基坑变形序列所有统计节点的作用，即避免Ns非整时的剩余节点浪费，再按长度s，对其进行逆序重新划分，共计得到2Ns个子区间。

(3)对各子区间进行方差求解，并计算q阶条件下的波动函数F(q，s)，即

(2)

式中：F2(s，v)为对应子区间v的方差；q为波动函数的阶次(设定为-10～10之间的偶数)。

(4)当区间长度s不同时，对应的F(q，s)也会不同，进而通过改变s，可得到若干散点(s，F(q，s))，两者的对数值具有线性关系，即

lnF(q,s)=C+h(q)lns。

(3)

式中：h(q)为q阶条件下的Hurst指数；C为拟合常数。

当q=2时，h(2)为经典Hurst指数，利用其值可进行基坑变形趋势的初步判断，这可与后续变形预测结果对比，以佐证其准确性。同时，h(2)的变形趋势判据为：当h(2)在[0，0.5)之间时，说明基坑发展趋势具反向持续性，即其发展趋势与现有变形趋势相反，且其值越小，趋势性越强；当h(2)=0.5时，说明分析结果具有游离性，无法判别基坑变形的发展趋势；当h(2)在(0.5，1.0]之间时，说明基坑发展趋势具正向持续性，即其发展趋势与现有变形趋势相同，且其值越大，趋势性越强。

(5)由于阶次q与h(q)存在一一对应关系，对(q，h(q))进行最小二乘拟合及求导，可得奇异指数a的表达式为

a(q)=h(q)+qh′(q) 。

(4)

式中h′(q)为q阶条件下的导函数。

以奇异指数a为基础，分别求解多重分形谱宽度参数Δa和波形中大小波动所占比例参数Δf(a)，即：

Δa=amax-amin；

(5)

Δf(a)=Δf(amax)-Δf(amin) 。

(6)

式中amax、amin分别为奇异指数a的最大值、最小值。

参数Δa用于表征多重分形谱宽度，其值越大，说明多重分形强度越强，且波动越剧烈；参数Δf(a) 用于表征波形中大小波动所占比例，其值越大，说明小波动波形所占比例越大。结合文献[4]、文献[5]及笔者工程经验总结，将上述两参数作为基坑预警等级划分的判据指标，其判别标准设定如表1所示。

表1 基坑预警等级判别标准Table 1 Criteria for early warning level of foundation pit

据表1判据，仍需评价2个判别指标的发展趋势，且鉴于Spearman秩次检验具有操作简单、准确性高等优点，利用其实现两判别指标的变化趋势判断。在Spearman秩次检验过程中，若将判别指标Δa或Δf(a)的变化序列表示为{X1，X2，…，Xn}，对其按大小重新排序，得新序列{Y1，Y2，…，Yn}，通过两序列计算得到秩系数rs，即

(7)

式中n为样本总数。

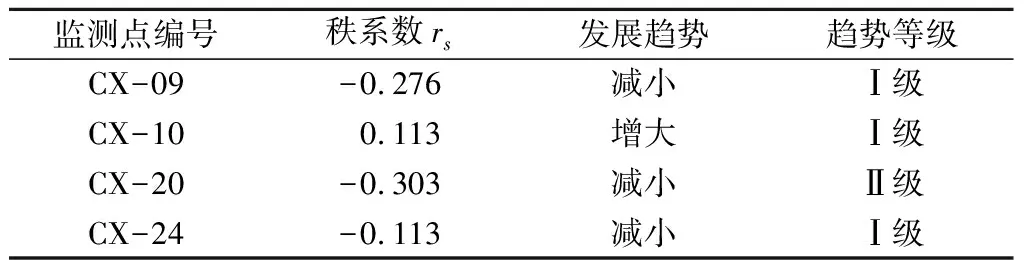
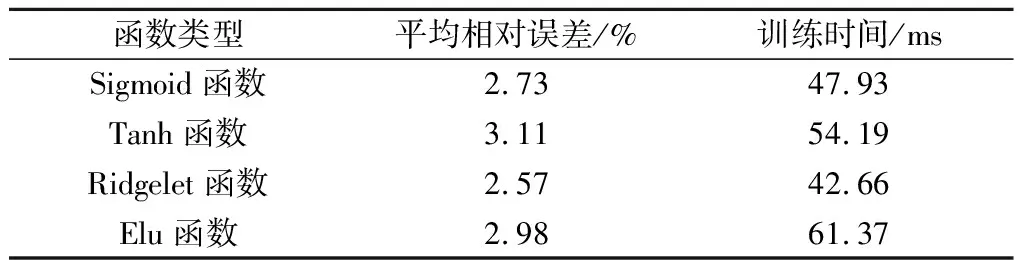
其次，将秩系数rs与临界值Wp进行对比，以判别Δa或Δf(a)指标的变化趋势，即：当rs为正时，说明判别指标具有增大趋势；反之，具有减小趋势。同时，当|rs|

由于临界值Wp由样本总数n及检验水平决定，鉴于样本总数n已是定值，进而可利用检验水平划分判别指标的变化趋势等级，标准如表2所示。

2.2 变形预测模型的构建

由于脊波神经网络采用最新的逼近复变函数，其具有明确的方向性，能准确处理高维数据的预测问题，属新型神经网络，相较传统神经网络模型具有

表2 判别指标的变化趋势等级划分Table 2 Classification of change trend of discrimination index

更高的理论优势；加之文献[11]已初步验证其在基坑变形预测中的适用性，因此，本文以其为基础构建基坑侧位移预测模型。同时，限于篇幅，加之其基本原理已在文献[11]中进行了详述，本文不再赘述。

在脊波神经网络的应用过程中，其相关模型参数多依赖于使用者经验，难以保证其客观性，有必要对其进行优化处理。通过总结，将脊波神经网络的待优化问题总结如下。

2.2.1 激励函数优化

脊波神经网络常用的激励函数有4种，即Sigmoid函数、Tanh函数、Ridgelet函数和Elu函数，各类激励函数的应用原理存在一定差异，进而对实例的适用性也存在不同。为保证激励函数的最优性，本文提出利用试错法进行优化筛选，即对4种激励函数的预测效果均进行计算，选取效果最优者作为本文预测模型的激励函数。

2.2.2 粗集理论的参数优化

脊波函数的位置、尺度及方位是其非线性特征的直观体现，对预测效果具有较大影响；鉴于粗集理论具有泛化能力强、学习能力高等优点，利用其优化脊波函数的位置、尺度及方位参数。

粗集理论优化能有效扩充神经元的使用系统，达到其他网络达不到的逼近空间，进而达到提高预测精度的目的。

最后，为实现预测效果的综合评价，本文将预测效果评价指标设定为平均相对误差和训练时间，前者用于评价预测模型的预测精度，后者用于评价预测模型的训练速度，两者相互综合，以实现预测效果的综合评价。

3 实例分析

3.1 工程概况

安元西路站隶属苏州地铁四号线，其基坑设计里程为DK2+266.1—DK2+532.7m，外包长度266.6m，标准段宽度、深度分别为19.7m和16.5m。基坑所处区域属典型水网化平原，水系较为发育，地势较平坦，场区高程在2.36～3.31m之间。同时，结合钻探成果，基坑开挖范围内的地层主要可分为素填土层、黏土层、粉质黏土层、粉质黏土夹粉土层、黏土层。

据室内试验成果，得出区内工程施工影响范围内的土体具有软土特征，这对施工影响较大，应予以切实关注和研究。

同时，根据水文调查成果，将区内地表水及地下水的基本特征分述如下：

(1)地表水。区内及附近无明显地表水体，主要以网状积水沟为主，其水位受降雨影响较大，主要接受降雨及地下水补给，对工程施工影响有限。

(2)地下水。按埋藏条件划分，区内地下水主要可分为孔隙潜水、微承压水和承压水3类。

为保证施工安全，在基坑施工过程中，对其进行了变形监测，其中，侧位移监测共计布设32个监测点，每个监测点布设深度为28m，具体布置如图1所示。

图1 基坑侧位移变形监测点布置Fig.1 Layout of monitoring points for side displacement and deformation

3.2 变形特性分析

据基坑侧位移监测成果，对各监测点的最大侧位移进行统计，得到图2。由图2可知，基坑侧位移变形具“驼峰”特征，结合图1中的监测点布置情况，得出在基坑端头两侧的侧位移相对偏小，而在基坑东、西两侧中部的侧位移相对偏大，分析原因可知其应与基坑支护结构强度相关。其中，在基坑端头，基坑开挖临空面尺寸相对较小，加之斜撑布设较多，使之具有较强的结构强度，有效限制了侧位移发展；基坑东、西两侧的基坑开挖临空面尺寸相对较大，加之其侧位移限制多依赖于横撑，使得其结构强度相对偏弱。

同时，再对基坑支护的相对侧位移δ/He进行统计(δ为基坑最大侧位移，He为基坑开挖深度)，得其特征参数如表3所示。

图2 基坑侧位移变形对比统计Fig.2 Comparison and statistics of side displacement and deformation of foundation pit

据文献[12]统计37个基坑的监测成果，得出基坑相对侧位移在0.041%～0.945%之间，而在本次实例安元西路站基坑中，相对侧位移为0.032%～0.108%；加之相对侧位移的平均值及标准差分别为0.074%和0.019%，说明其相对侧位移明显小于前者统计结果，侧面反映了安元西路站基坑支护结构的合理性和有效性。

表3 基坑相对侧位移特征参数统计Table 3 Statistics of characteristic parameters of relative side displacement of foundation pit

3.3 变形预警分析

利用MF-DFA分析和Spearman秩次检验进行基坑侧位移变形预警分级，以评价其预警等级；同时，在分析过程中，为保证分析结果的准确性，分别选取东、西两侧变形相对较大的CX-09、CX-10、CX-20和CX-24监测点进行分析。首先，利用MF-DFA分析求解不同阶次条件下的Hurst指数，结果如表4所示。

表4 不同阶次条件下的MF-DFA分析结果Table 4 MF-DFA analysis results under different order conditions

由表4可知，随各监测点的阶次减小，Hurst指数也在逐步减小，说明基坑侧位移变形具有多重分形特征；当q=2时，各监测点的h(2)值均>0.5，说明基坑侧位移发展趋势具正向持续性。结合基坑侧位移现有变形趋势，得出基坑侧位移仍会继续增加，且CX-20监测点的趋势性相对最强，其次是CX-09监测点、CX-10监测点和CX-24监测点。

其次，在前述分析基础上，计算多重分形谱宽度参数Δa和波形中大小波动所占比例参数Δf(a)，并利用Spearman秩次检验判别两者的变化趋势。通过计算，得两者的分析结果如下：

多重分形谱宽度参数Δa的Spearman秩次检验结果如表5所示。由表5可知，4个监测点的秩系数rs均>0，说明其均具增大趋势，且CX-09监测点和CX-20监测点的趋势等级为 Ⅱ 级，其余2个监测点的趋势等级为 Ⅰ 级。因此，得出各监测点的多重分形谱宽度参数均呈增大趋势，但趋势性强度一般。

表5 多重分形谱宽度参数的变化趋势判断结果Table 5 Judgment results of variation trend of multifractal spectrum width parameters

类比前述，再对波形中大小波动所占比例参数Δf(a)进行Spearman秩次检验，结果如表6所示。

表6 波形中大小波动所占比例参数的变化趋势判断结果Table 6 Judgment results of change trend of proportion parameters of size fluctuation in waveform

由表6可知，除CX-10监测点的Δf(a)具有增大趋势以外，其余监测点均呈减小趋势，且仅CX-20监测点的趋势等级为Ⅱ级，其余监测点的趋势等级均为Ⅰ级。因此，得出Δf(a)以减小趋势为主，且趋势性强度偏弱。

最后，以Δa和Δf(a)的变化趋势判断结果为基础，结合表1中的判别标准，综合得出基坑侧位移预警等级判断结果，如表7所示。由表7可知，两类判据指标具有的预警等级特征存在一定差异，多以1级预警特征为主，两者综合，得出CX-09监测点和CX-20监测点的综合预警等级为2级，其余两监测点的综合预警等级均为1级。

综合上述侧位移预警等级分析结果，按不利原则，确定基坑侧位移预警等级为2级，说明其变形趋于不利方向发展，具有预警前兆信号，应加强监测频率，提高施工安全预警。

表7 基坑侧位移综合预警等级判断结果Table 7 Judgment results of comprehensive early warning level for side displacement of foundation pit

3.4 变形预测分析

为进一步佐证前述分析结果，也为提出一种新的预测思路，再以脊波神经网络构建基坑侧位移预测模型；在优化或预测过程中，以2 d为1个周期，将1—40周期作为训练样本，41—45周期作为验证样本，并外推预测46—49周期。

3.4.1 优化效果对比分析

限于篇幅，仅以CX-09监测点为例，详述各阶段的优化过程及其效果，具体分述如下：

先将隐层层数设定为1层，求得不同激励函数的预测效果，如表8所示。由表8可知，不同激励函数的预测精度及训练时间存在一定差异，验证了激励函数优化筛选的必要性。对比4类激励函数的预测效果，得出Ridgelet函数不仅具有相对最小的平均相对误差，还具有相对最短的训练时间，其次是Sigmoid函数、Elu函数和Tanh函数。因此，确定本文脊波神经网络的激励函数为Ridgelet函数。

表8 不同激励函数的预测效果对比Table 8 Comparison of prediction results among different excitation functions

其次，再利用粗集理论优化脊波函数的位置、尺度及方位参数，以实现预测模型参数的全面优化；且为对比本文预测模型的优越性，利用传统BP神经网络进行对比预测，结果如表9所示。

据表9，在相应验证节点处，本文预测模型的相对误差均偏小，加之本文预测模型的平均相对误差仅为1.89%，而传统BP神经网络的平均相对误差为2.79%，本文模型预测精度相对更高，且该预测模型具有相对更短的训练时间，验证了预测模型的优越性；对比表9和表10，得出经粗集理论优化，虽对训练时间的优化效果一般，但预测精度具有明显提高，验证了该步优化的必要性；通过外推预测，得出CX-09监测点的侧位移仍呈增加趋势，这与前述MF-DFA分析h(2)的趋势分析结果一致，初步佐证了本文两类分析方法的准确性。

表9 CX-09监测点的最终预测结果Table 9 Final prediction results for CX-09 monitoring point

表10 可靠性预测分析结果Table 10 Results of reliability prediction analysis

3.4.2 预测效果的验证分析

前述不同优化阶段的预测效果对比已初步验证了本文预测思路的合理性，为进一步检验其可靠性，本文再对其余3个监测点进行可靠性验证分析，结果如表10所示。由表10可知，3个验证监测点的预测效果相当，其中，在预测精度方面，以CX-12监测点的预测精度最高，其平均相对误差为1.71%;其次是CX-10监测点和CX-11监测点，且其最大平均相对误差也仅为1.93%，说明预测模型的预测精度具有较强的可靠性；在训练时间方面，得出三者的训练时间在48.29～54.38 ms之间，均相对较短，且差异不大。因此，综合得出本文预测模型不仅具有较高的预测精度，还具有很好的可靠性，值得推广应用。

据外推预测结果，3个验证监测点的侧位移也呈不同程度的增加趋势，这也与前述预警分析结果一致。

上述分析验证了本文预测模型的有效性，所得预测结果与前述预警结果一致，均得出安元西路站的侧位移将会继续增加。为保证施工安全，建议加强监测频率，提高施工安全预警。

4 结 论

通过安元西路站基坑的侧位移变形预警及预测研究，主要得出如下结论：

(1)基坑最大侧位移主要发生于基坑长边中部，这与其结构强度相关，即基坑支护体系的结构强度越高，侧位移变形越不明显；反之，侧位移变形越显著。因此，基坑设计过程应注重支护结构强度的均一性，以控制侧位移变形处于合理范围内。

(2)MF-DFA分析能有效评价基坑侧位移的发展趋势，结合Spearman秩次检验的分析能力，能合理构建出基坑侧位移变形预警模型，得出其预警等级为1～2级之间，说明其变形趋于不利方向发展，应加强监测预警。

(3)脊波神经网络具有较强的预测能力，通过多阶段参数优化，不仅能进一步提高预测精度，还能增加其稳健性，为基坑变形预测提供了一种新的思路，且预测结果与前述预警结果一致，佐证了本文分析结果的准确性。