基于压力拱理论的双洞隧道最小净距弹塑性分析

宋 蕾 付晨涛

(1.西安科技大学高新学院城市建设学院，陕西 西安 710054；2.启迪设计集团股份有限公司，陕西 西安 710054)

随着我国隧道建设的飞速发展，单洞隧道已难满足运输需求，隧道由最初的小直径单洞隧道发展至现在的超大直径双洞隧道，双洞隧道之间的间距取值规范虽有明确，但是实践表明，在目前某些特定的工况下规范的间距取值依旧过于保守，因此，选取双洞隧道间的最优净距是目前迫切需要研究的问题。

当前的研究中，净距的取值多集中在利用数值模拟、现场实际量测和模型模拟方法。而在理论分析方面主要是运用复变函数Schwarz转换的相关数学知识，推导出应力场，从而确定合理净距。

本文以弹塑性理论为基础进行分析，将双洞隧道中间岩柱划分成塑性区和中间核区，利用普氏压力拱理论的相关原理，对双洞隧道中间岩柱体应力分布进行合理化简，从而确定出双洞隧道最小净距的计算公式。

1 双洞隧道压力拱理论

1.1 双洞隧道压力拱的形式

压力拱的形成分以下两种极限状况[1]。

隧道开挖方式，中间岩柱体加固措施合理的情况下，会提高加固后的中间岩柱体承载能力，有效防止岩柱体上方土体的下沉，缩小了压力拱的影响范围，在该状态下，双洞隧道只能出现单侧洞压力拱，且左右隧道的压力拱影响范围互不干扰。

隧道开挖方式，中间岩柱体加固措施不妥的情况下，会导致中间岩柱体承载能力降低，随着岩体上方土体的逐步下沉，这导致了左右洞室的压力拱影响范围逐渐扩大，直至最后在洞室上空两个压力拱相互重合，这就是极限压力拱的形成。

本文采用第二种极限工况下的双洞隧道受力形式，来分析探讨双洞隧道的重力荷载分布情况。

1.2 压力拱高度的取值

普氏理论认为，在松散岩体中进行隧道开挖，隧道上方会形成一个抛物线压力拱用于承受上部岩体的重力荷载，而作用在隧道支护结构上的围岩压力仅为压力拱内岩体的自重。

2 双洞隧道物理模型的建立

此处考虑侧压力系数为1的情况，由卡斯特纳公式[2]可知，单洞隧道塑性区半径如下：

式1

则单洞隧道塑性区范围为：

式2

将双洞隧道中间岩柱划分成塑性区和中间核区，这里选取中间岩柱宽为s，高L=2ra为研究对象，如图1所示。

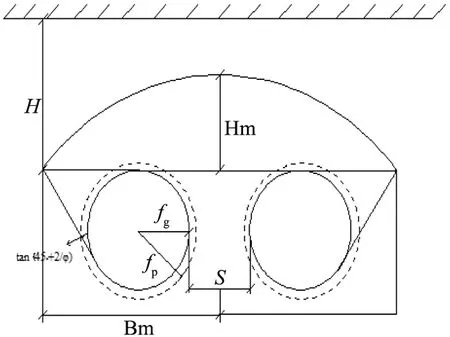
图1 双洞隧道物理模型

3 建立中间岩柱的力学模型

根据摩尔库伦准则和静力平衡方程得到无支护圆形洞室塑性区应力计算表达式[2]。

式3

根据式3中环向应力公式得在塑性区与中间核区的交界处的环向应力等于当r=rp时的环向应力值，中间岩柱核区边界处所受竖向应力为。

式4

两侧隧道会对中间岩柱的应力大小产生影响，设中间岩柱塑性区的应力大小是从0线性增长到核心区岩柱所能承受的最大应力，且核心区应力大小保持不变。该应力分布如图2所示。

图2 中间岩柱的应力分布图

这里将围岩压力拱内的重力荷载分布简化为矩形分布，当隧道开始开挖后，认为两侧隧道(各一半)的重力荷载将分配到中间岩柱上[3]。

4 双洞隧道最小净距公式的推导

由图2中应力分布曲线可知，中间岩柱受力为：

式5

利用普氏理论求得极限压力拱高度为：

式6

通过荷载简化，假定荷载在隧道拱顶呈矩形分布，中间岩柱所受的荷载高度为Hm，推导出中间岩柱所受重力荷载为：

式7

由式5和式7相等，赋值分析得双洞隧道最小净距为

式8

5 参数分析

本文以Ⅲ级围岩常见的物理力学参数为例，分析式8中各个物理量对双洞隧道最小净距的影响关系，得到以下结论。

最小净距随重度的增大而非线性增大，但在Ⅲ级围岩条件下基本呈线性关系且重度对最小净距取值影响不大。

最小净距随粘聚力及内摩擦角的增大而呈非线性减小的趋势，且该参数对隧道净距的取值影响较大。

当计算内摩擦角逐渐增大时，最小净距的变化呈非线性减小，且非线性变化并不明显，所以该参数对双洞隧道最小净距影响较小。

随着隧道埋深逐渐变大，最小净距的变化成非线性增大，在Ⅲ级围岩条件下非线性趋势明显。根据实际情况，在Ⅲ级围岩条件下开挖双洞隧道时，隧道净距应取0.5D较为合理。

6 小 结

将中间岩柱分为塑性区和中间核区，基于压力拱理论与弹塑性理论相结合，得到了双洞隧道最小净距确定公式8。

对式8中所涉及到的物理力学参数进行分析，分别得到最小净距与各参数之间的关系；本文给出的推导利用了压力拱理论，且考虑了埋深对净距的影响使中间岩柱的尺寸更加优化，对提高经济效益和隧道施工安全有着重要意义。