移动网络中多用户下行非相干MIMO通信

林梦莹，郑 霖，杨 超

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.广西无线宽带通信与信号处理重点实验室，广西 桂林 541004)

0 引言

多用户多输入多输出(Multiple Users Multiple Inputs Multiple Outputs，MU-MIMO)技术因能够采用空分多址方式在相同的时间和频率资源上与多个用户进行通信[1]，实现比时分多址方式更高的系统容量，已经成为IEEE802.11ac、802.11ax和5G无线传输的关键技术。当前研究的MU-MIMO系统大多数采用基于实时准确信道估计的相干检测方式[2]。在快衰落、高速移动等复杂环境下，精确的信道估计、相偏和频偏补偿算法对硬件系统的要求较高。而非相干检测无需实时精确的信道估计，不受相位噪声的影响，可以降低接收机的复杂度，减少系统的开销。

现阶段对MU-MIMO非相干检测算法的研究中多数是基于差分编码，包括差分空时分组码[3]、差分酉空时调制[4]。文献[5]提出了一种基于差分空时分组码的下行链路非相干检测算法，在基站和用户处均不需要信道状态信息，降低了收发机的复杂度。但在用户数量很大的情况下，该算法会导致正交扩展码的长度过长，从而增大系统的开销。文献[6]针对MU-MIMO下行系统，提出在发射端对信号进行叠加编码，接收端通过串行干扰抵消方法解调下行信道互干扰。文献[7-8]提出在大规模MU-MIMO下行系统中采用差分下行传输，提出一种基于功率空间分布信息的预编码器用于多用户干扰消除，收发两端都不依赖于信道状态信息，在接收端采用决策反馈差分技术检测信号，具有较低的复杂度。

上述基于差分编码主要针对的是分集多用户MIMO下行系统，且通常假设在码块传输期间信道响应保持准静态而且是空间上不相关的，在高速移动场景下，这样的假设难以成立。

信道的快时变性主要源于高速移动产生的多普勒频移及多普勒扩展，为了降低多普勒频移的影响，学者们提出了非相干能量检测算法[9-10]。文献[11]提出了一种低复杂度能量检测接收机，它利用了接收分集支路的衰落增益的大小，推导了其误符号率表达式，结果表明，基于部分信道信息的能量检测方案性能明显优于完全不需要信道状态信息的非相干检测方案，且还能保持非相干检测器的低复杂度结构。文献[12]提出基于ASK调制的能量检测接收机，推导了高信噪比条件下加权包络检测接收机的近似误符号率的闭合表达式。文献[13]提出一种基于Chirp-BOK调制的最佳随相检测算法，避免了信道引入的随机相位影响。文献[14]提出一种基于MFSK调制的MIMO能量检测算法，该非相干能量检测算法可以抵抗随机相位的干扰、多普勒频偏。文献[15]将文献[14]中的非相干能量检测系统模型进一步简化，提出了随相检测系统模型，在接收端解调信号时，其具有更低的复杂度。

上述基于平方律非线性处理的能量检测算法不仅具有复杂度低、抗多普勒频移的特点，且可以获得较大的空分复用增益，但研究针对的是点对点MIMO通信，尚未有文献研究其在多用户环境下的可行性，对于如何解决多个用户复用信道产生的多用户干扰问题也尚未涉及。

本文以文献[12]为基础，研究非相干MIMO检测算法在多用户环境下的应用问题。首先针对多普勒频移一致性问题，讨论了非相干MIMO空分复用算法在多用户MIMO上行系统和下行系统中的可行性。然后从理论和仿真上分别验证了常规线性预编码技术可以有效解决非相干MU-MIMO系统的干扰问题。结合预编码干扰消除技术，非相干MIMO空分复用检测算法在多用户环境下具有很好的抗多普勒频移的性能。

1 MIMO-FSK非相干空分复用

1.1 信道模型

对于高铁通信、地空通信和车地通信，其信道是典型莱斯信道，信道矩阵H(t)可以表示为：

(1)

式中，Hs(t)表示视距分量；Hd(t)表示散射分量。当β=0时，到达接收机的信号全部是视距信号。假设MIMO系统有N根发射天线和M根接收天线，发射端与接收端之间属于远场传输，所有的通道可以视为具有一致的多普勒频移[16-17]。采用的信道模型表示为：

(2)

式中，ejφ(t)表示多普勒频移引起的相位旋转因子。

1.2 MIMO FSK随相检测

假设MIMO系统有N根发射天线和M根接收天线。在该系统中，第n根发射天线的第w个FSK符号表示为：

snw(t)=(1-cnw)ej2πf1t+cnwej2πf2t，

(3)

式中，f1,f2分别表示2个正交频率；cnw={0,1}表示第n根发射天线的第w个二进制码元，发送信号矩阵S的第w列表示为：

(4)

接收信号可以表示为：

Y=HS+N，

(5)

式中，Y为接收信号矩阵，维度为M×T；S为发送信号矩阵，维度为N×T，T表示一个符号时长；N为高斯白噪声，则第m根接收天线的第w个符号可以表示为：

ymw=hmsw+nmw，

(6)

式中，hm表示H的第m行；sw表示发送端的第w个码元，因此ymw可以表示为：

(7)

式中，ejφ(t)表示多普勒频移引起的相位旋转因子，在一个符号时间内看作是常数ejφ。对ymw(t)做随相处理，得到：

(8)

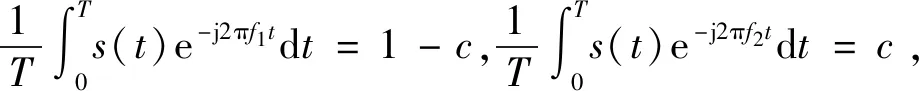
(9)

最终的接收信号可以表示为：

(m,w)，

(10)

(11)

MIMO系统的等效信道矩阵为：

=R(∑H)，

(12)

式中，R(·)表示取实部；∑为对角矩阵，且∑kk=hk1e-jθk1+hk2e-jθk2+…hkNe-jθkN。则经过随相处理后，MIMO系统可以等效为：

=+。

(13)

从推导结果看，虽然MIMO FSK非相干空分复用检测系统采用了非线性平方律处理，但系统仍然可以等效为一个线性实系统，且等效信道矩阵和等效信号维度没有发生改变，可以采用常规的线性检测算法。

2 下行链路非相干MU-MIMO

2.1 非相干MU-MIMO的可行性分析

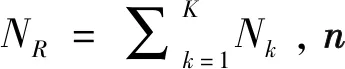
在MU-MIMO上行系统中，令xk∈Nk×1表示第k个用户的信号，k=1,…,K，yMAC∈Nk×1表示基站的接收信号，NT×Nk表示第k个用户和基站之间的信道矩阵，那么接收信号可以表示为：

(14)

由模型可知，基站接收的信号都是来自所有用户的信号，由于各个用户具有不同相对运动方向、运动速度，导致各用户的信号到达基站的多普勒频移不一致，得到：

(15)

式中，φmn，φmj表示的是任意不同用户的2路信号到达基站时的相位变化。由于φmn≠φmj，这会造成等效矩阵的变形，造成检测性能的恶化。因此，MIMO-FSK随相处理算法不适用于上行链路。

在MU-MIMO下行系统中，令x∈NR×1表示基站给所有用户发送的信号，yk∈Nk×1表示第k个用户的接收信号，Nk×NT表示第k个用户和基站之间的信道矩阵，那么第k个用户的接收信号可以表示为：

(16)

从用户k来看，其接收到的信号x全部来自基站，信号x的多普勒频移仅仅和用户k与基站之间的相对运动方向和速度有关，即在一个符号时长内，所有信号都具有一致的相位变化，得到：

(17)

式中，φmn，φmj表示的是基站发送给用户k的任意2路信号的相位变化，由于φmn=φmj，其等效矩阵并未发生改变。在多用户MIMO下行系统中，虽然各个用户具有不同的运动方向和速度，多普勒频移不一致，但不会影响用户k对接收信号做非相干随相处理，接收端的等效系统模型不会改变。因此MIMO-FSK随相处理算法可以用于多用户MIMO下行链路。

2.2 MU-MIMO下行链路预编码论证

假设多用户MIMO经过预编码后的系统等效为一个NT发NR收的系统，且NT=NR，定义全局编码信道矩阵为：

(18)

式中，H是实际的信道矩阵；F是所有用户的预编码向量所构成的矩阵，经过平方律随相处理后，全局的等效编码信道矩阵为：

(19)

式中，R(·)表示取实部；(·)*表示取共轭；∑A为对角矩阵，其第k个对角元素可以表示为Σkk=ak1e-jθk1+ak2e-jθk2+…+akNTe-jθkNT，k=1,2,…,NR。

当用户接收端为单天线时，称之为MU-MISO系统。要求经过随相处理后全局的等效编码信道G为一个单位矩阵，假设∑AA是一个对角矩阵，因为∑A为对角阵，因此可以得到A是一个对角矩阵。且有：

(20)

因为A是一个对角矩阵，有akje-jθkj(j≠k)=0，则对式(20)有：

(21)

即要求预编码矩阵F满足：

|A|=|HF|=I，

(22)

式中，|·|表示对矩阵各个元素取模值。可以得到随相处理系统预编码的充分条件：

F=HH(HHH)-1，

(23)

(24)

由此可见，式(23)仍然满足式(24)。基于随相处理的MU-MISO系统仍然可以采用迫零预编码算法。同理，对于MU-MIMO系统可以采用块对角化算法[1]。

3 仿真分析

通过仿真验证迫零预编码、块对角化算法在多用户MIMO下行随相处理系统中的可行性。通过仿真分析高铁信道下随相处理在多用户MIMO下行链路的性能，将其与PSK相干检测进行比较。MIMO FSK随相处理系统发射端均采用V-BLAST编码和FSK调制。用户数用K表示，假设FSK带宽B=2.5 MHz，采样速率为Fs=20 MHz，符号速率Rb=1.25 MHz，每一帧包括1 000个数据符号和20个训练符号。

迫零预编码MU-MISO系统和SISO系统性能如图1所示。

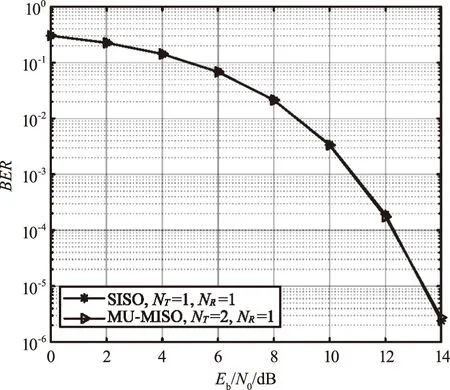
图1 迫零预编码MU-MISO系统和SISO系统性能Fig.1 The performance of zero-forcing precoding MU-MISO system and SISO system

由图1可知，当MU-MISO系统在发送端进行迫零预编码时，用户的性能与SISO系统的性能曲线几乎重合，当Eb/N0>14 dB时，其误码性能在10-5以下。由于在MU-MISO系统的发射端采用迫零预编码消除多用户干扰会使得MU-MISO系统失去发射分集增益，因此其性能与SISO系统的性能一致。MU-MIMO系统和SU-MIMO系统性能比较图如图2所示。

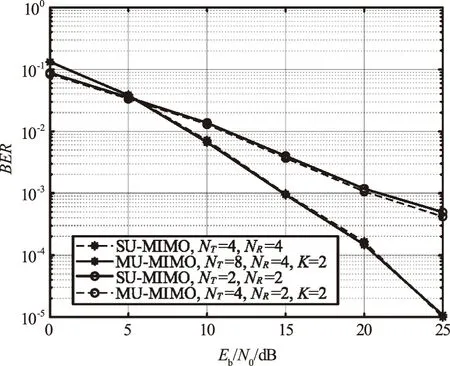
图2 块对角化预编码MU-MIMO系统和SU-MIMO系统性能Fig.2 The performance of block diagonalization precoding MU-MIMO system and SU-MIMO system

MU-MIMO下行链路发射端经过块对角化算法预编码后，接收端的用户性能与SU-MIMO随相检测系统的性能一致，说明在多用户MIMO随相处理系统采用块对角化预编码可以完全消除共信道干扰。

高铁信道下MU-MIMO下行链路中FSK非相干随相处理与PSK相干检测的BER性能对比图如图3所示。假设发射天线数为8，有2个用户，其接收天线数均为4。仿真采用了文献[14]中的高铁信道模型，采用了块对角化预编码算法。fD表示多普勒频移，莱斯因子为10 dB。FSK与PSK采用相同的带宽和码元速率。随着fD增大，信道相干时间减小，对于固定帧长的PSK相干检测系统而言，其BER性能急剧下降，在fD=0.04 kHz时，其误码率性能接近10-2。相比而言，当Eb/N0>15 dB时，FSK非相干检测系统的性能在10-3以下。信道相干时间减小对FSK非相干检测系统的影响不大，但当fD=0.43 kHz时，巨大的多普勒频移导致接收端检测频率不匹配，也会使得其系统性能急剧下降。

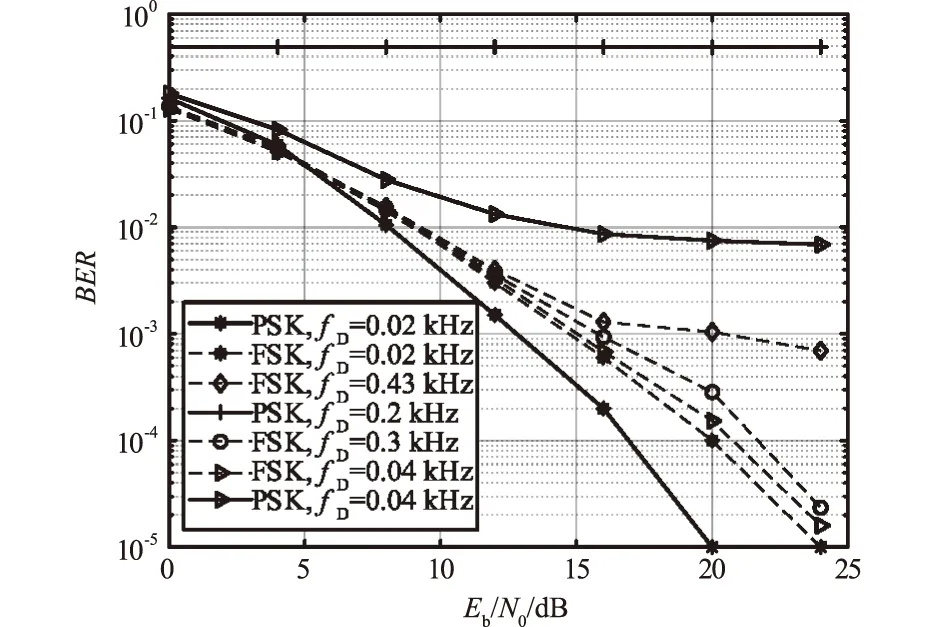
图3 高铁信道下MU-MIMO FSK和MU-MIMO PSK性能Fig.3 The performance of MU-MIMO FSK and MU-MIMO PSK in high-speed railway channel

4 结束语

本文解决了基于能量检测的非相干MIMO检测算法应用在多用户环境下所面临的问题，包括其可行性以及多用户共信道干扰问题。由于该检测算法要求信号的多普勒频移具有一致性，因此其适用于多用户下行系统。虽然基于平方律处理的非相干能量检测算法会造成非线性干扰，但经过理论推导和仿真分析可以验证常规线性迫零预编码算法、块对角化预编码算法仍然是消除多用户干扰的有效方法。此外，非相干MIMO能量检测的抗多普勒频移特性使得多用户MIMO系统的预编码矩阵不需要跟踪多普勒频移的实时变化。下一步研究如何降低发射端对精确信道状态信息的依赖。