初中生活数学类拓展性课程课堂数学活动特征研究——基于名师教学视频分析
斯海霞,孔梦蝶,叶立军
初中生活数学类拓展性课程课堂数学活动特征研究——基于名师教学视频分析
斯海霞1,孔梦蝶2,叶立军1
(1.杭州师范大学 经亨颐教师教育学院,浙江 杭州 311121;2.浙江省温州市平阳县昆阳镇第二中学,浙江 温州 325400)
从数学活动视角出发,以省级名师拓展性课程课堂教学展示课为研究对象,对初中生活数学类拓展性课程课堂数学活动设计及组织特征进行分析.研究发现生活数学类拓展课中,数学活动设计需逐层经历五层次数学化全过程,不仅在情境层次与应用层次加强了生活与数学的双向联系,更侧重于指涉层次与形式层次以突出数学本质;课堂呈现“两环五步”式学习模式彰显学为中心理念,“动静”结合的教学互动以引导学生“数学地思维”.研究建议在生活数学类拓展课中,整体有序地设计五层次数学化活动,为学生搭建数学“再创造”的深度学习路径;有效耦合数学现实与形式,以充分发挥数学学科育人功能;师生共建教学共同体,引导学生亲历数学化过程以促进素养形成.
初中数学拓展性课程;数学化活动;生活数学;活动组织
为满足学生个性化、多元化发展需求,拓展性课程逐渐成为中小学校课程的重要组成部分[1].近20年来,湖南、上海、浙江等地虽已着力开发各类拓展性课程内容、编写教材,但课程教学设计及实施水平仍有待提高[2-5],特别是知识类拓展性课程,易异化为基础课程教学内容的巩固与加深.初中数学拓展性课程是对基础性课程的拓展延伸,旨在激发学生学习兴趣,拓展学生知识面,发展学生数学核心素养[6].相较于数学基础性课程教学有明确的知识技能为学习载体,且有概念课、命题课、技能课等教学模式,可用以帮助教师有效设计教学,数学拓展性课程教学则仍处于经验摸索与积累阶段[7-9].
有研究者从课程性质出发,提出数学拓展性课程的课堂应当具有教学内容主题化、教学活动思维化等特征[1],其中的数学活动设计是该类课程教学促进学生素养形成的主要路径[10-11].虽然数学活动常被设计为基础性课程教学的某一环节,但教师缺少用一课时设计、实施主题性数学活动课的教学经验.即使在初中数学基础性课程教材中,设置了诸如“探究活动”“课题学习”等数学活动专栏,由于教师缺乏指导、借鉴,评价滞后等原因,这类数学活动课往往陷入“高价值低使用”的尴尬境地[8,12-13].因此,围绕各类数学拓展性课程教学活动主题,教师如何改革传统育人模式,以一课时为单位,切实有效地设计、组织相应的数学活动过程及学习方式,成为推进数学拓展性课程建设与实施进程,提高其教学有效性的重点课题[4].
考虑到“生活数学类”拓展课是一线初中数学教师实施拓展性课程教学的首选主题,这类课题通常由现实情境导入数学教学活动,是促进数学知识技能转化为数学素养的重要载体[10,14].研究者从Z省初中数学名师拓展性课程教学观摩研讨课中,择选两节同课异构的生活数学类拓展课进行案例分析,提炼素养驱动下该类拓展性课程课堂数学活动设计、开展方式,以期为教师设计数学拓展性课程教学提供参考.
1 研究设计
1.1 研究问题
已有研究者使用数学建模流程设计素养指向的生活数学类拓展性课程教学[8],但对于教师如何设计具体数学活动,如何逐步引导学生经历现实情境数学化,进而解决问题回应现实仍有待深入研究.因此,研究将聚焦如下问题:(1)生活数学类拓展性课程教学中数学活动应如何设计、开展?(2)教师如何组织学生参与到数学活动过程中,以促使数学核心素养培育落地?
1.2 研究对象
Z省教研室联合省内各地数学教研员、特级教师与高校数学教育学者,编写出版了初中数学拓展性课程教材《数学新探索》,并于2019年组织省内名师开展基于教材的拓展性课程教学观摩研讨活动.择选该活动中两位名师同课异构的生活数学类拓展课进行分析.其中任课教师A为Z省特级教师,教师B为H市名师(中学高级),授课内容皆选自《数学新探索》九上第四章相似三角形,课题同为生活数学类拓展性课“实际问题数学化:探索A4纸的数学秘密”(1课时).课前学生已经学完Z教版初中数学基础性课程内容“相似三角形”.
1.3 分析框架
数学化是生活数学类教学活动最主要的特征,该过程不仅包括从学生的数学现实出发,逐步经历数学化直至形式化,以发展学生数学思维,也应包括由形式化数学向现实的“复归”[15].教师设计、组织开展数学化活动的效果决定数学核心素养的落实水平[16].因此,结合上述两个研究问题,研究者从数学化“活动设计”与“活动组织”两个维度构建分析框架,并借鉴已有的相关研究[17-19],将具体分析框架确定如表1所示.

表1 分析框架
“活动设计”主要从数学“活动任务”“活动类型”“活动层次”3个子维度分析教师如何设计、开展数学活动.其中的“活动任务”分为标准性题、训练性题、探索性题与问题性题[20];结合教学现场观察,将“活动类型”聚焦于解答活动与实验活动;依据已有学者提出的数学化四层次及斯托利亚尔提出的数学活动三阶段,将“活动层次”分为情境层次、指涉层次、普遍层次、形式层次[21]、应用层次,活动情境分析蕴含其中.
“活动组织”主要从“学习形式”与“互动模式”两个子维度揭示教师如何组织学生参与到数学活动过程中.其中“学习形式”分为自主探究、小组合作、全班交流、反思归纳4个步骤[18];“互动模式”分为课堂教学4类关键的师生互动行为[19],即教师提问—学生应答、学生提问—教师应答、教师讲解—学生听讲、学生做题—教师辅导.已有课堂教学行为研究表明,这4类互动通常以教师提问—学生应答为主,为更好地揭示教学互动行为特征,研究围绕“教师提问”“学生应答”及“教师反馈”这3个指标展开具体分析.其中“教师提问”按其思考性功能分为联系性提问、理解性提问、拓展性提问、归纳性提问[22],此外新增两类用于管理课堂纪律的管理性提问与常识性提问[23];“学生应答”与“教师反馈”主要分析学生在学习活动过程中表达程度与反馈深度,具体分类借鉴美国“TRU”课堂评价模型[24].
1.4 编码及数据分析
借鉴TIMSS Video Study的录像编码和视频案例研究方法,通过现场观察和视频拍摄相结合的方式记录两位授课教师的课堂教学.请3位研究生反复观看录像,对教师课堂活动过程及师生行为进行实录、编码、分类,并对有疑问的编码进行三角论证,以最终达成一致.结合R语言实现层次性分析,得出相关研究结果.
此外,根据分析框架,研究对上述两节生活数学类课与数学思想方法类课的数据进行聚类分析,分类结果与教学主题一致,研究结果具有一定的代表性.
2 研究结果与分析
2.1 活动设计特征
(1)深入设计五层次数学化活动,加强形式数学向现实生活的复归以践行学科育人.
在数学基础性课程教学中,学生参与某一数学化活动常常浅尝辄止.研究中两位教师引导学生围绕“探索A4纸的数学秘密”这一活动主题,在一课时里深度参与了五层次数学化全过程.具体活动设计及开展方式如表2所示.

表2 数学化教学进程架构
首先,以学生已掌握的相似三角形章节知识为基础,引导学生从数学视角出发,对A4纸的设计进行深度研究,凸显生活数学主题特征.其次,引导学生逐层经历五层次数学化活动,并在首、尾层次的数学活动中加强客观世界与数学世界间的相互联系.两节课中虽然部分任务【如任务(1)、(2)】设计细节有所不同,但整体上教师都围绕A4纸的几何特征设计探索性的测量、计算任务,引导学生先经历情境层次与指涉层次,将有关A4纸的情境问题初步数学化;随后设计标准性问题抵达普遍层次,给出标准纸概念;进而在形式层次通过训练性的推测解释类解答活动,引导学生采用数学逻辑推理方法研究标准纸的性质与判定;最后再利用探索性的信息技术类或数学类实验活动,即通过折A4纸的方式,探究正方形与A4纸直接的关系.特别是教师B,在应用层次加强了形式数学向现实生活的复归,用数学形式化研究结果分析了A4纸设计蕴含的绿色环保价值取向,践行了学科育人功能.
(2)各层次活动时间分配呈“M”型,侧重指涉层次与形式层次,以突出数学本质.
两位教师在课中都带领学生经历了5个层次的数学化活动,但5个层次时间分配有差异.研究以5个层次活动教学所用时间为分析数据,用R语言进行层次性分析(检测指标分别为0.00、0.001).如图1所示,两位教师在情境层次与普遍层次时间权重较为接近,即用几分钟的时间,快速地引导学生借鉴几何研究的方法分析A4纸的特点,继而进入指涉层次.在随后的学习活动中,教师A在指涉层次所用的教学时间权重最高,即引导学生动手探究A4纸边长的数量关系,其次是在应用层次与形式层次;教师B则在用以探究标准纸性质的形式层次时间权重最高,其次为指涉层次与应用层次.由于普遍层次只是呈现标准纸的概念,其时间权重皆为最低.

图1 两节课各层次所用时间分析结果
结合表2可知,虽然教师A在应用层次用了较多的时间,但主要是探究A4纸与正方形的相互关系.相比而言,教师B在情境层次与应用层次更完整地展示了数学来源于生活又服务于生活的探究过程.当然,生活数学类拓展性课在突出数学生活化的同时,更应注重数学化研究过程,引导学生学会用数学的思维去思考现实世界.因此,综合两位教师的数学活动时间分配,建议设计指涉层次、形式层次时间权重相对较高,其次是情境层次与应用层次,普遍层次依然最低,其时间权重分布上如图1“期望”折线所示,大致呈现“M”型.
2.2 活动组织特征
活动组织特征主要揭示教师针对上述数学活动,如何组织学生亲历数学化过程,进行数学“再创造”[25].
(1)注重学生自主探究与合作交流,“两环五步”式学习彰显了以学为中心.
研究首先从学习活动组织形式、互动模式分析活动组织特征.两节课中学习组织形式整体上呈现了“两环五步”的基本结构.如图2所示,从数学活动的情境层次至普遍层次,学生整体上经历了一次教师引导下的“全班交流—自主探究—小组合作—全班交流—反思归纳”学习过程,进而得出标准纸概念.进入形式层次后,教师再次引导学生以“全班交流—自主探究(或小组合作)—全班交流”的形式投入学习,直至应用层次,以探索标准纸的性质及其应用,并在最后以“反思归纳”的形式结束课题学习.其中自主探究前的全班交流通常较为简短,教师快速地引导学生注意并投入到数学活动中开展自主探究.

图2 “两环五步”学习模式
此外,研究以两节课各学习形式所占时间作为数据,用R语言进行层次性分析(检测指标为别为0.005、0.001),结果如图3、图4所示.两节课中“全班交流”所用时间权重皆最高,分别为65%与67%.而全班交流又以“教师提问—学生应答”互动为主,其次为“教师讲解—学生听讲”.课堂是教学师生双边互动的主要场所,为更好地揭示教学互动特征,下文聚焦时间权重最高的“教师提问—学生应答”互动模式进行深入分析.

图3 教师A学习组织形式权重分布

图4 教师B学习组织形式权重分布
(2)针对性地设计提问反馈与等待,“动静”结合式互动引导学生“数学地思维”.
数学活动是通过师生、生生交流互动,逐步完成数学化的思维活动[26].研究中的教学互动以师生互动为主,而“提问—思考(等待)—应答—反馈”又是其中最主要的师生互动方式.事实上,由于初中学生正处在由具体形象思维向抽象逻辑思维转化的阶段,课堂中的师生互动除了动态的师生“提问—应答”互动,也在一定程度上体现为积极、静态的内动式“倾听与思考”.为有效促进学生的课堂参与度(包括倾听、思考、应答程度),研究中教师的提问、等待及反馈行为亦皆具针对性与多样性.
图5中教师的提问统计不仅包括组织数学活动时进行的设疑提问,也包括对学生应答进行反馈时的追问.教师A与教师B提问总量分别为273与137,两位教师在课堂中主要使用联系性提问与理解性提问激励学生思考,其次是常识性提问、归纳性提问及拓展性提问,用于维持课堂教学秩序的管理性提问极少出现.在教学过程中,当学生接触新的学习内容时,两位教师常采用联系性问题,引导学生将当前学习内容与已学内容进行联系,如在课题学习之初引导学生回忆以前如何研究几何图形,进而类比研究A4纸;当学生遇到学习困惑,或处在理解关键点时,教师又以设问或追问的形式提出理解性问题,如“根据你们刚才的操作,可以发现标准纸还有什么性质?”等.

图5 两节课各类提问百分比分布
数学活动不只是一种有趣的探索活动,更需要静心思考钻研.从研究提炼的“提问—等待(思考)思考—应答—反馈”过程上看(如图6所示),教师在提问后,通常会给予学生一定时间思考探索,特别是教师B在拓展性与归纳性提问后,给学生充分的思考时间(如图7、图8所示).教学互动“动静”结合,以帮助学生理清思路、内化数学活动,提高数学思维品质.教师在提问、等待后,学生会做出不同的应答,主要是沉默或是较短的发言.当学生沉默无表达时,教师主要通过追问或是自己回答的方式进行反馈,以引导学生深入思考.当学生有表达时,教师以深入分析为主,其次是重复应答与重复问题、引导学生总结对错.上述师生互动推动着学生在参与数学化过程中学会“数学地思维”.
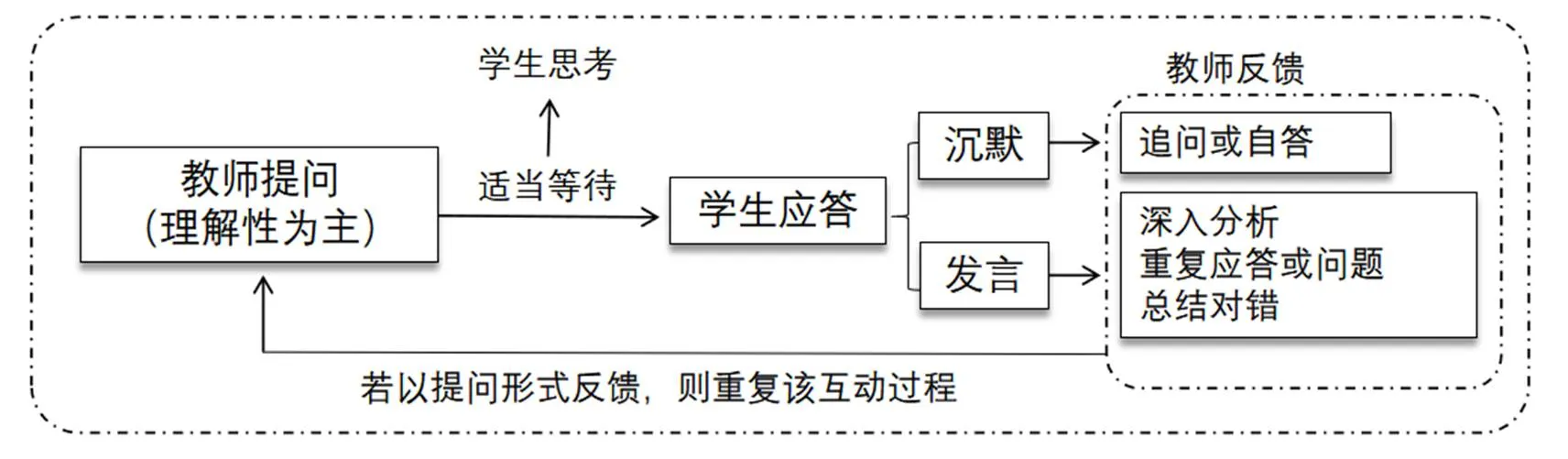
图6 师生问答反馈互动过程

图7 教师A提问与等待时间比较

图8 教师B提问与等待时间比较
3 启示
(1)整体有序设计五层次数学化活动,搭建数学“再创造”的深度学习路径.
数学核心素养是学生经历数学化活动过程中习得的数学思维方式、关键能力及必备品格,数学学科知识与数学思维经验是数学核心素养最重要的源泉与基础[27].因此,有效的数学化活动是基于学生已有的知识和经验,引导学生经历数学“再创造”[26],进行数学地思维.两位教师在生活数学类拓展性课程教学中,以相似三角形为基础,皆有效地设计了五层次数学化活动,为学生搭建了数学“再创造”的深度学习路径.
教学中的数学活动引领学生用数学的研究方法深度分析现实材料,以揭示隐藏在数学现实背后的数学思维方式,帮助学生在巩固基础性知识的同时,积累数学探索、思考感悟的学习经验.当然,数学化5个层次教学亦有侧重,虽然在首、尾层次需加强现实生活素材与形式数学的联系,但教学活动设计更应注重逐层数学化过程,特别是在指涉层次与形式层次,以提高学生数学思维的深刻性、严密性.
(2)有效耦合数学现实与形式,充分发挥生活数学的学科育人价值.
数学知识的过度形式化和抽象化是课堂学习“惰性知识”产生的根源,而现实情境素材则是提高数学知识活力与价值、发展学生数学核心素养的重要载体.教学中五层次数学化活动逐层展开,并在首、尾层次通过揭示生活数学与形式数学的相互联系与区别,有效地耦合了数学现实与形式,充分发挥了生活数学化的德育价值.
(3)师生共建教学共同体,亲历数学化过程以促进素养形成.
数学核心素养的形成和发展本质上是学生在参与数学化活动过程中“悟”出来的,是在教师引领下,学生围绕具有挑战性的学习主题,通过独立思考、互动交流逐渐形成的思维品质[28].研究中师生共同营造了一个以五层次数学化活动为课堂结构支架,以“两环五步”为学习形式,以对话、合作、交往为特征的交互式教学环境,即教学共同体,这是学生亲历、内化数学化活动,发展数学核心素养的重要学习场域.
依托教学共同体,学生在逐层数学化的学习任务引领下,通过“两环五步”学习形式,经由问、等、答、馈等互动行为,完整经历数学化全过程.该过程不仅体现了生活数学类拓展性课程学习的挑战性、体验性与迁移性,也激发了学生在课程学习中的主体性、能动性与发展性,是提高学生思维自觉性,促进学生核心素养培育落地的重要路径.
4 结语
两位教师在生活数学类拓展性课程教学中创生教学共同体,带领学生逐层、深入地经历了五层次数学化全过程.该过程侧重在指涉层次与形式层次突出数学本质,强调在情境层次与应用层次加强生活与数学的双向联系,以践行数学学科育人功能.教师通过组织“两环五步”学习形式与“问、等、答、馈”等互动行为,引导学生在参与上述数学化活动过程中,逐渐学会用数学的眼光看世界,用数学的思维思考世界,用数学的语言表达世界.当然,拓展性课程课题活动不止于生活数学类,如数学实验、知识拓展、数学思想方法等其它类型的拓展性课程数学活动特征,有待今后继续深入实践研究.
[1] 叶立军,董婷婷.义务教育阶段数学拓展性课程教学特征及策略研究[J].中小学教师培训,2019(4):56-58.
[2] “拓展性课程研究”课题组.拓展性课程研究实验报告[J].湖南师范大学教育科学学报,2002(1):53-55.
[3] 陈小芳,陆佳.拓展型课程执行的现状、问题及其反思[J].教育参考,2016(3):106-112.
[4] 柯孔标.义务教育拓展性课程的理论与实践探索[J].课程·教材·教法,2019,39(3):30-35.
[5] 斯海霞,叶立军.浙教版初中数学拓展性课程教材编写特点及改进建议[J].数学教育学报,2019,28(6):16-20.
[6] 浙江省教育厅.关于建设义务教育拓展性课程的指导意见[EB/OL].(2015-12-01)[2019-12-02]. http://www.zjedu. gov.cn/news/142778441751261711.html,2015.
[7] 何萍,章才岔.初中数学拓展性课程开发与实施情况调查研究[J].中学数学月刊,2018(11):38-40.
[8] 邵文鸿,周建忠.基于数学素养发展的初中拓展性课程的构建与实施研究[J].中学教研(数学),2018(6):9-13.
[9] 张安军.玩游戏学数学——一个八年级拓展性课程的实践[J].数学通报,2017,56(4):20-24,43.
[10] 余文森.核心素养导向的课堂教学[M].上海:上海教育出版社,2017:70-72.
[11] 孔凡哲.中国学生发展的数学核心素养概念界定及养成途径[J].教育科学研究,2017(6):5-11.
[12] 李莎,李芒.对我国综合实践活动课程实施现状的反思[J].课程·教材·教法,2004,24(9):11-15.
[13] 帅建卓.初中数学活动课文献综述[J].中学数学杂志,2018(6):25-28.
[14] 常磊.情境视角下的数学核心素养[J].数学教育学报,2017,26(4):24-28.
[15] 郑毓信.数学教育哲学[M].南宁:广西教育出版社,2008:59.
[16] 刘月霞,郭华.深度学习:走向核心素养[M].北京:教育科学出版社,2018:86.
[17] 徐斌艳.高中数学教材探究内容的分析指标体系及比较研究[J].课程·教材·教法,2012,32(10):35-40.
[18] 许芬英.学为中心的初中数学课堂特征和教学基本模式初探[J].课程·教材·教法,2014,34(5):53-57.
[19] 曹一鸣,于国文.中学数学课堂教学行为关键性层级研究[J].数学教育学报,2017,26(1):1-6.
[20] 鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:175.
[21] 张国祥.数学化与数学现实思想[J].数学教育学报,2005,14(1):35-37.
[22] 许芬英,潘小梅.学为中心的初中数学思考性问题类型及其设计[J].数学通报,2016,55(10):13-17.
[23] 叶立军,胡琴竹,斯海霞.录像分析背景下的代数课堂教学提问研究[J].数学教育学报,2010,19(3):32-34.
[24] 周九诗,鲍建生.美国“TRU”课堂评价模型介绍及其启示[J].外国中小学教育,2016(12):52-56.
[25] 徐斌艳.“现实数学教育”中基于情境性问题的教学模式分析[J].外国教育资料,2000(4):28-33.
[26] 邓友祥.数学活动的特质与有效教学策略[J].课程·教材·教法,2009,29(8):38-42.
[27] 余文森.论学科核心素养形成的机制[J].课程·教材·教法,2018,38(1):4-11.
[28] 史宁中,林玉慈,陶剑,等.关于高中数学教育中数学核心素养——史宁中访谈之七[J].课程·教材·教法,2017,37(4):8-14.
A Study of Mathematics Activities of a Life-Oriented Mathematics Enrichment Curriculum in Junior High School Classrooms——Based on the Video Analysis of Expert Teachers
SI Hai-xia1, KONG Meng-die2, YE Li-jun1
(1. Jing Hengyi Teacher Education College of Hangzhou Normal University, Zhejiang Hangzhou 311121, China;2. Second Middle School, Kunyang Town, Pingyang County, Zhejiang Wenzhou 325400, China)
From the perspective of mathematics activity, we studied the demonstration lessons of provincial expert teachers and analyzed the design and organizational characteristics of mathematics activities in a junior high school life-oriented mathematics enrichment curriculum. It was found that the design of mathematics activities centered on the theme of life goes step-by-step through the five-level process mathematicization and focuses on the level of reference and form in order to highlight the essence of mathematics. The organization of activities reflects the learning model of “two links and five procedures” and teaching interaction is characterized by the combination of “static and dynamic” so as to lead students to “think mathematically.” In this study, we suggest designing the five levels of mathematics activities in a holistic and orderly way, combining the reality and form of mathematics effectively, embodying the moral value of life-oriented mathematics, building a joint teaching community of teachers and students, building a deep learning path for students to achieve mathematics “re-creation,” and guiding students to go through the process of mathematics to promote mathematical core literacy.
enrichment curriculum in junior high school; mathematics activity; life-oriented mathematics; organization of activities
2021-01-15
浙江省教育厅省级产学合作协同育人项目——产教融合视阈下师范院校《数学实验》课程建设实践探索(ZJ2020106);2020年杭州市教师教育科研项目——“PSTE”合作模式下教师专业发展实践研究(JSJY2020004);杭州师范大学教学研究项目——基于教学设计中的中学数学特级教师教学风格研究(085C5021820439)
斯海霞(1986—),女,浙江嵊州人,讲师,博士,主要从事中小学数学课堂教学研究.
G632.4
A
1004-9894(2021)04-0035-06
斯海霞,孔梦蝶,叶立军.初中生活数学类拓展性课程课堂数学活动特征研究——基于名师教学视频分析[J].数学教育学报,2021,30(4):35-40.
[责任编校:陈汉君、陈隽]

