基于互补式集合经验模态分解和SSA-ELM的短期风电功率预测

魏鹏飞，樊小朝，史瑞静，2，王维庆，闫亚东

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.新疆工程学院，新疆 乌鲁木齐 830023；3.国网乌鲁木齐市供电公司，新疆 乌鲁木齐 830011)

0 引 言

我国现如今积极推动风能发电，减少碳排放，把促进风能的发展视为保障人类、社会和经济可持续发展的一项重要举措。截至2019年底，全国风电累计装机容量达2.1亿kW，风电发电量达4 057亿kW·h,占全部发电量的5.5%[1]。然而，风电功率的波动性和非平稳性给电网调度和调节带来了挑战，高效的风电功率预测既能提高电网并网能力以及安全性，还能有效的减少弃风[2]。目前，短期风电功率预测可分为两类。一类是依据历史数据建立的物理统计模型[3-5]；另一类是运用智能算法建立的学习模型。如支持向量机和改进的原子搜索算法相结合[6]、粒子群算法优化核极限学习机[7]、长短时记忆网络[8]。但是这些模型有较大的局限性，随着预测时间的加长，直接导致预测误差不断增大。所以，本文提出一种基于CEEMD和SSA-ELM的新型短期风电功率预测的方法。欲借助CEEMD对历史风功率数据进行分解；随后结合SSA-ELM建立适应各个分量的预测模型进行预测叠加；最后对未来短时间的风电功率进行仿真预测。

1 互补式集合经验模态分解

现阶段用于信号预处理有经验模态分解(EMD)、小波变换和傅里叶变换3种方法。后2种方法极为相似，均采用固定的函数基来进行分解。小波变换对于不同的信号的分析需要选用不同的小波基才能达到理想效果，但是EMD的自适应正交基处理方法恰好解决了这个问题。EMD对于未知的信号可以直接进行分解，不需要人为干预。EMD可将未知信号分解为

(1)

式中，xt表示原始信号；m为内涵模态分量(IMF)分量的总数；imfj(t)表示第j个IMF分量；r(t)表示剩余分量。

由于EMD会在一个模态中产生不同的局部特性振荡或者在不同的模态中产生相同的局部特性振荡。为此Huang等对原始信号添加高斯白噪音来填充整个空间，即为集合经验模态分解(EEMD)方法，以此来减少振荡的产生[9]。但是重构的信号内包含了残余噪声，对不同信号分量IMF进行运算时会导致虚假分量的产生，直接影响对最终信号的分析。Yeh等随后在加入相同数量的等幅值白噪音后，EEMD的残余噪声随之减小，大大缓解了重建问题[10]。不论分解次数的多少，CEEMD总能将残余噪音维持在一个很小的程度。所以CEEMD在保证残余噪音干扰小的前提下，还能够节省计算时间。

2 樽海鞘群优化算法

Mirjalili等于2017年提出樽海鞘群算法(SSA)[11]。该算法模拟了深海中樽海鞘的链式群行为，即多个个体首尾相连，形成一条“链”[12]，并由链前端的领导个体带领着众多追随者个体进行移动和捕食。追随者的移动仅受制于前一个樽海鞘的影响，这就使得樽海鞘链具有很强的全局搜索能力和局部开发的能力。基于樽海鞘链式群行为做出的新算法，可以避免算法陷入局部最优的情况。

(2)

(3)

式中，t是当前迭代次数。c2和c3是区间[0，1]的随机数，c2决定算法的移动长度，c3决定算法的移动方向。追随者的运动位移

(4)

(5)

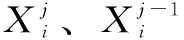
由于SSA收敛速度快、寻优效率高等诸多优点，相关研究呈大幅度增长，并广泛运用到医疗、救援、军事、教育等领域。其中运用在发电系统的有基于数据预处理技术、预测算法和樽海鞘群优化算法建立了风速预测模型[13]。该模型有效地解决了风速预报问题，获得了较高的精度和较强的稳定性，而且性能优于其他组合模型。

3 极限学习机

极限学习机(ELM)与传统的神经网络相比，在训练阶段采用随机的初始化输入层权值和偏差。这使得ELM具有所需训练参数少、简单易用、学习进度和逼近能力快等优点。此次使用ELM的目的是高效提取特征值并高准确率的预测。

假设样本集(Xi，ti)∈(Rn，Rm)，i=1，2，…，N，其中Xi=[xi1，xi2，…，xin]T，ti=[ti1，ti2，…，tim]T。对于单隐层神经网络含L个隐藏节点可表示为

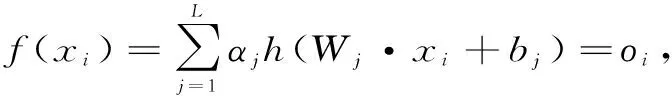
(6)

式中，αj为输出权重；h(x)为激活函数；Wj为输入权重；bj为隐藏单元偏置。

当输出无误差时，则有

(7)

矩阵形式表达为

HB=T

(8)

式中，H为隐层节点的输出；B为输出权重；T为期望输出。

4 CEEMD与SSA-ELM短期风电功率预测模型

首先借助CEEMD方法对历史数据做出分解，得到频率明显的各个分量，随后搭建SSA-ELM对各个分量进行预测，最后将各个预测值整合叠加获得最终的风电功率预测结果。预测模型的建立过程如图1所示。

为了验证模型的仿真预测效果，文中以平均绝对误差MAE、均方根误差RMSE、平均绝对百分误差MAPE作为评价指标。

(9)

(10)

(11)

式中，n为预测样本数；pt为预测绝对误差；Pt为真实值。

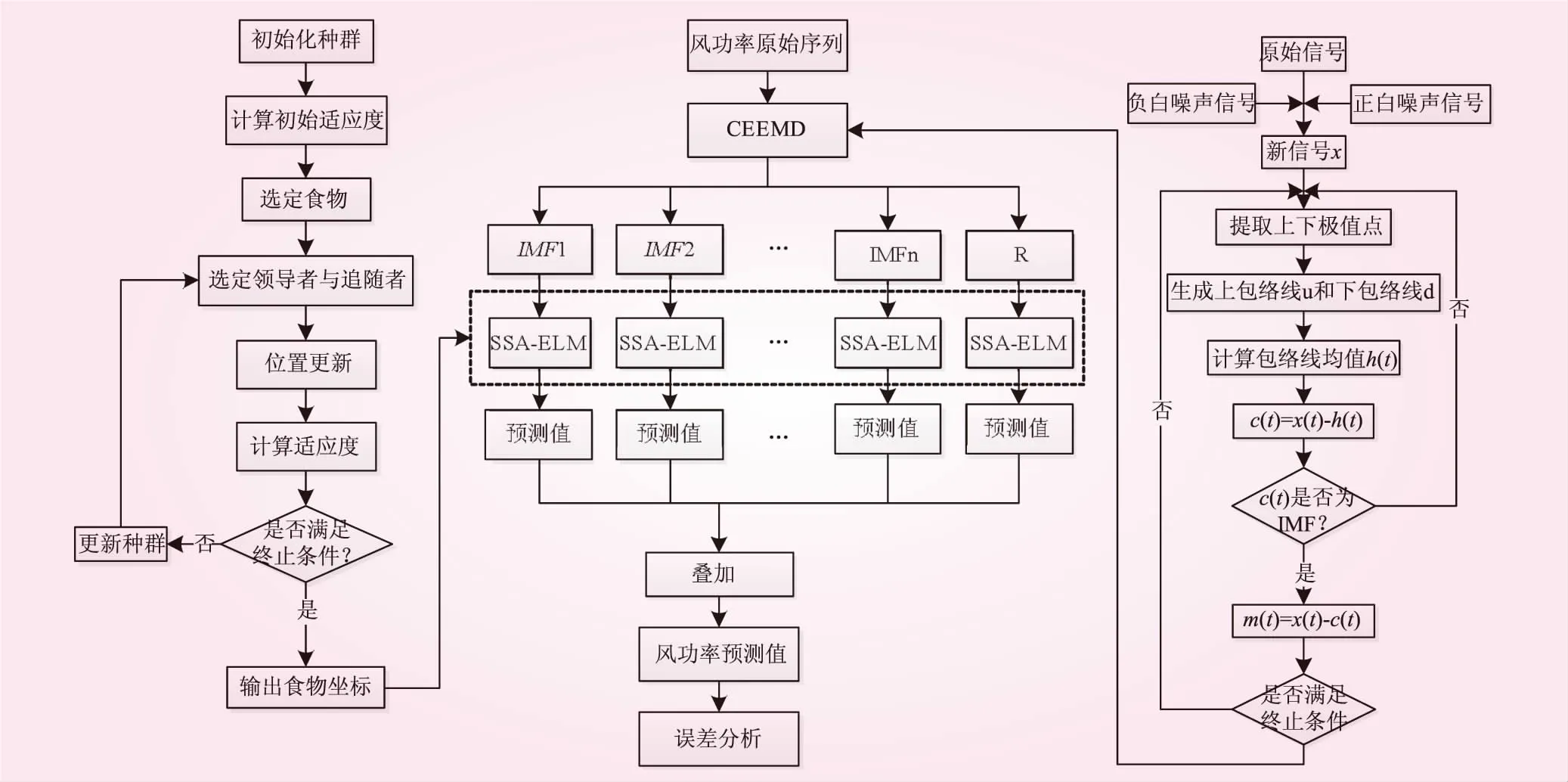
图1 CEEMD-SSA-ELM短期风功率预测模型

5 算例仿真与结果分析

5.1 样本选择与分解

本文选择国内某风电场历史风功率数据作为训练样本进行仿真分析，采样区间为5 min，共选取2 500个样本点作为CEEMD-SSA-ELM预测模型的仿真样本数据。原始风功率信号如图2所示。

图2 原始风功率信号

CEEMD分解中，加入成对高斯白噪音的标准差为0.2，白噪声次数为50。CEEMD分解结果如图3所示，固态模态分量从高频到低频共11个分量，剩余分量为R。从IMF4开始，固定模态分量曲线周期逐渐变长，周期性逐渐明显。

图3 CEEMD对原始风功率分解结果

5.2 预测结果分析

对CEEMD分解得到的各个固态模态分量与剩余分量建立多个预测模型，预测未来的130个样本点。本模型设定樽海鞘算法的搜索动因子数为30，最大迭代次数为200，极限学习机的隐含层数节点数量初始化为300，激活函数选用‘sig’。为了对比验证CEEMD-SSA-ELM对短期风功率预测的精准性和有效性，还分别建立ELM、SSA-ELM、EMD-SSA-ELM、EEMD-SSA-ELM四种预测模型进行仿真对比分析，结果如图4所示。由图4对比可以看出基于CEEMD-SSA-ELM模型的短期风功率预测结果曲线拟合效果最好，预测精准度最高，预测效果最好。通过SSA算法优化后的ELM的预测曲线精准度优于未优化的ELM，说明SSA对ELM的输入权值和隐含层数的优化有明显的促进。通过EMD、EEMD、CEEMD等分解方法对原始波动性大、非线性的风功率信号进行预处理的组合预测模型，其预测曲线精准度明显高于单一预测模型，说明优先对波动性大且非线性的信号预处理，能够有效提高其预测精度。通过CEEMD-SSA-ELM、EMD-SSA-ELM、EEMD-SSA-ELM三种组合预测模型的结果对比，说明CEEMD分解在加入了成对的正负白噪音后，既能弥补EMD分解中的频率混叠和局部振荡的缺点，又能弥补EEMD分解中白噪音引起的虚假分量的问题，对预测结果的精准度有促进作用。

图4 不同预测模型预测值与真实值对比

试验结果显示CEEMD-SSA-ELM组合预测模型的MAE、RMSE和MAPE分别为0.104 3、0.142 5和0.919%，其中CEEMD-SSA-ELM组合预测模型的MAPE与ELM、SSA-ELM、EMD-SSA-ELM、EEMD-SSA-ELM相比分别降低了3.348 6%、2.298%、0.233 6%、0.087 2%。这说明CEEMD-SSA-ELM预测模型在短期风电功率预测中曲线拟合程度更好，预测精度更高。

6 结 语

针对实际中风电功率的波动性问题，首先选用互补式集合经验模态分解法对原始不稳定的风功率样本进行分解得到不同的模态分量，通过加入成对白噪音既能解决传统分解法的振荡问题，又能解决经验模态分解法的精度不够的问题。另外，本文运用樽海鞘群算法简单易实现、收敛速度快、寻优效率高、易于计算机实现等优点来优化极限学习机。通过算例仿真比较，该模型的建立具有一定的工程价值，能为短期风电功率的预测提供可靠的预测结果，有较高的实用价值。