考虑不确定性的电动汽车动力电池逆向物流网络设计

刘娟娟 郭炎可

摘要：考虑到电动汽车动力电池回收量、回收技术水平等参数的不确定性，以逆向物流网络总利润最高和环境影响最小为目标，建立多目标模糊规划模型，进行电动汽车动力电池逆向物流网络设计。利用基于可信性测度的模糊求解方法处理模型中的模糊参数。引入决策者偏好系数，采用加权理想点法将多目标模型转化为单目标模型进行求解，得到考虑不确定性的逆向物流网络设施的选址、数量以及设施间的废旧动力电池流量分配方案。通过数值算例验证模型和算法的可行性和有效性。对回收量、回收技术水平和决策者偏好系数进行灵敏度分析，结果表明：随着回收量的增加，逆向物流网络利润增加;回收技术水平的提升和决策者选择合适的偏好系数可以提高逆向物流网络的经济效益和环境效益。

关键词：

电动汽车动力电池; 逆向物流; 网络设计; 模糊规划

中图分类号：  F252;X705

文献标志码：  A

收稿日期： 2020-06-21

修回日期： 2020-11-20

基金项目： 国家社会科学基金（15BGL084）

作者简介：

刘娟娟（1973—），女，山西闻喜人，副教授，博士，研究方向为物流与供应链管理，（E-mail）jjliu@shmtu.edu.cn

Design of reverse logistics network for electric vehicle power battery considering uncertainty

LIU Juanjuan， GUO Yanke

（School of Economics & Management， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

Considering the uncertainty of recovery quantity， recovery technology level and other parameters of electric vehicle power battery， a multi-objective fuzzy programming model is established to design the reverse logistics network of electric vehicle power battery with the objectives of the maximum total profit and the minimum environmental impact. The fuzzy parameters in the model are processed by the fuzzy solution method based on the credibility measure. By introducing the preference coefficient of decision makers， the multi-objective model is transformed into a single-objective model by the weighted ideal point method. The location and quantity of facilities and the waste power battery flow distribution scheme between facilities of reverse logistics network considering uncertainty are obtained. The feasibility and validity of the model and algorithm are verified by a numerical example. The sensitivity analysis on the recovery quantity， the recovery technology level and the decision makers preference coefficient shows that the reverse logistics network profit increases with the increase of recovery quantity， and the improvement of the recovery technology level and decision makers selecting an appropriate preference coefficient can improve the economic and environmental benefits of the reverse logistics network.

Key words：

electric vehicle power battery; reverse logistics; network design; fuzzy programming

0 引 言

近年來，随着全社会对能源转型和环境保护的日益重视，电动汽车的推广成为解决能源短缺和环境污染的一种方案。动力电池作为电动汽车的重要组件之一，销量迅猛增长。据中国汽车技术研究中心估算，到2025年我国电动汽车动力电池年报废量或达35万t。由于废旧动力电池中含有有毒电解液以及重金属（钴、镍、铜），将其随意丢弃或做不规范处理不仅白白浪费资源，而且会对水和土壤造成严重污染，回收利用废旧动力电池则可以延长电池的生命周期、减少环境污染。然而，国内废旧动力电池回收点分散、混乱，且废旧动力电池资源化利用企业少，导致其回收量不高，回收过程产生了大量污染物。这严重影响了废旧动力电池回收经济效益和环境效益的实现，不利于我国动力电池产业的长远发展。2019年11月，工业和信息化部发布的《新能源汽车动力蓄电池回收服务网点建设和运营指南》对废旧动力电池逆向物流网络的建设提出了要求，因此，设计有效的废旧动力电池回收体系以及可靠的逆向物流网络具有重大的社会意义。

动力电池再利用方面的研究成果主要有：ASSUNO等[1]评估了废旧动力电池回收利用的投资可行性，并提出将废旧动力电池回收再造后用于能源存储能够产生经济效益。李敬等[2]分析了我国废旧动力电池回收产业的现状和回收利用的经济性，并提出了相应的管理意见。张雷等[3]的研究进一步表明动力电池梯次利用具有巨大商业价值。BEER等[4]认为将废旧动力电池集中回收处理有利于实现经济效益和环境效益。刘怡君等[5]基于循环经济视角对电动汽车动力电池逆向物流链进行了优化，提出了废旧动力电池有效回收利用的合理方式。朱广燕等[6]针对国内外电动汽车动力电池的回收和梯次利用现状，对我国废旧动力电池回收的发展方向提出了建议。

为实现电动汽车动力电池的循环利用，逆向物流网络的合理性和经济可行性至关重要。确定设施的位置、数量以及设施间的废旧动力电池流量分配方案是网络设计的关键[7]。LI等[8]针对动力电池的再制造问题，建立了以网络利润最高为目标的闭环供应链网络模型。CHEN等[9]认为减少碳排放是实现可持续发展的重点，构建了考虑总成本和碳排放的双目标混合整数规划模型。程发新等[10]以水泥企业为例，研究了碳税政策约束下企业多目标再制造物流网络优化问题。上述逆向物流网络设计未考虑逆向物流系统的高度不确定性，而忽略不确定性进行的供应链网络设计会使企业面临巨大风险。在当前考虑不确定性的逆向物流网络研究中，大部分研究考虑的是客户需求和回收量的不确定性[7]。秦小辉[11]针对产品回收量的不确定性，对废旧家电逆向物流网络进行了优化设计。LEE等[12]研究了客户需求和回收量不确定条件下的逆向物流网络设计问题，提出一种两阶段随机规划模型。张群等[13]以废钢循环利用网络为研究对象，以成本最低和环境影响最小为目标建立了随机规划模型。周向红等[14]考虑再制造回收的不确定性，建立了自营回收模式下再制造逆向物流网络多目标规划模型，并利用模糊规划处理不确定性问题。考虑不确定性的逆向物流网络设计成为未来研究的热点问题[15]。

当前从经济效益和环境效益两方面考虑不确定性进行的动力电池逆向物流网络设计研究较少，综合考虑回收量、回收技术水平等多种不确定性因素的研究更少。此外，碳排放量是衡量温室气体对地球温室效应贡献度的一个基本指标，可将不同温室气体的排放量折算成对应的碳排放量，用于统一衡量温室气体对地球温室效应的影响[16]。基于此，本文以网络利润最高和碳排放量最小为目标，建立考虑动力电池回收量、回收技术水平等不确定因素的多目标规划模型，并利用模糊规划方法处理参数的不确定性。在此基础上，针对当前动力电池回收技术尚未成熟的情况，研究回收技术进步对供应链的影响;在动力电池回收产业发展的不同阶段，考虑决策者对经济效益和环境效益的偏好对逆向物流网络设计的影响。

1 模型构建

1.1 问题描述与模型假设

以电动汽车动力电池回收利用为背景，建立一个包括收集中心、再循环利用中心和回收中心的逆向物流网络模型，见图1。动力电池更换点（汽车修理店或4S店等）是废旧动力电池交易产生的地方，负责将动力电池运往收集中心。收集中心接收動力电池后对其进行质量检查，基于质检结果决定动力电池的后续处理方式。若动力电池能够被梯次利用，则被发往再循环利用中心，否则被运往回收中心。动力电池在再循环利用中心被加工修理和模块重组后，在其他领域继续使用。动力电池在回收中心被拆解，其所含有的重金属得到循环利用。假设：①单位处理成本、单位运输成本、单位价格、回收量和再循环利用比例等不确定参数采用三角模糊数表示;②运输成本与运输距离正相关。

1.2 模型参数和决策变量

1.2.1 模型参数

集合：动力电池更换点集合I={1，2，…，I}，i∈I;收集中心集合J={1，2，…，J}，j∈J;再循环利用中心集合K={1，2，…，K}，k∈K;回收中心集合M={1，2，…，M}，m∈M。

参数：fj、fk和fm分别为开设收集中心j、再循环利用中心k和回收中心m的固定成本;Hj、Hk和Hm分别为收集中心j、再循环利用中心k和回收中心m的最大年处理能力;j、k和m分别为收集中心j、再循环利用中心k和回收中心m对单位废旧电池的模糊处理成本;dij为动力电池更换点i与收集中心j之间的运输距离，类似的距离还有djk和djm;ij为从动力电池更换点i到收集中心j的单位电池的单位距离模糊运输成本，类似的模糊运输成本还有jk和jm;i为动力电池更换点i回收废旧电池的模糊数量;i为动力电池更换点i回收废旧电池产生的单位模糊成本;k为再循环利用中心k对电池进行梯次利用取得的单位模糊收入;m为回收中心m对电池中的金属进行循环利用取得的单位模糊收入;1为运往再循环利用中心的电池比例;2为运往回收中心的电池比例;ej、ek和em分别为开设收集中心j、再循环利用中心k和回收中心m的固定碳排放量;gj、gk和gm分别为收集中心j、再循环利用中心k和回收中心m处理单位电池产生的碳排放量;w为单位电池的单位运输距离碳排放量。

1.2.2 决策变量

将动力电池更换点作为消费点，研究收集中心、再循环利用中心和回收中心的设施位置、数量以及设施间的废旧动力电池流量分配。

决策变量：xj∈{0，1}，若开设收集中心j，则xj=1，否则xj=0;xk∈{0，1}，若开设再循环利用中心k，则xk=1，否则xk=0;xm∈{0，1}，若开设回收中心m，则xm=1，否则xm=0;Qij表示从动力电池更换点i运往收集中心j的电池数量;Qjk表示从收集中心j运往再循环利用中心k的电池数量;Qjm表示从收集中心j运往回收中心m的电池数量。

1.3 逆向物流网络设计模型

除有特殊说明外，动力电池逆向物流网络模型中下标的范围为i∈I，j∈J，k∈K，m∈M。

1.3.1 目标函数

目标1为逆向物流网络总利润最高：

max FF=F1-F2-F3

（1）

其中

F1=jkkQjk+jmmQjm

（2）

F2=jxj fj+kxk fk+mxm fm

（3）

F3=ij（j+dijij）Qij+jk（k+djkjk）Qjk+jm（m+djmjm）Qjm+iii

（4）

F1为动力电池梯次利用和拆解利用所获取的收入;F2为逆向物流设施固定建设成本;F3为对废旧动力电池的加工成本、运输成本和回收成本。

目标2为逆向物流网络碳排放量最小：

min ZZ=jejxj+kekxk+memxm+

ij（gj+dijw）Qij+jk（gk+djkw）Qjk+

jm（gm+djmw）Qjm

（5）

式（5）等号右边的前3项分别为收集中心、再循环利用中心和回收中心设施建设产生的碳排放量，后3项为动力电池在加工和运输过程中产生的碳排放量。

1.3.2 约束条件

i=jQij  （6）

1iQij=kQjk

（7）

2iQij=mQjm

（8）

iQij=kQjk+mQjm

（9）

iQij≤Hjxj

（10）

jQjk≤Hkxk  （11）

jQjm≤Hmxm  （12）

Qij，Qjk，Qjm≥0  （13）

xj，xk，xm∈{0，1}   （14）

式（6）保证所有动力电池更换点回收的废旧电池都被运往收集中心;式（7）和式（8）表示运往再循环利用中心和回收中心的电池应符合质量要求;式（9）为收集中心的动力电池流量平衡约束;式（10）～（12）依次为收集中心、再循环利用中心和回收中心的最大年处理能力约束;式（13）和（14）为决策变量约束。

2 模型求解

本文建立的动力电池回收利用多目标模糊规划模型涉及对不确定参数和多目标的处理，为便于求解，将其转化为确定型混合整数规划模型。

2.1 模型转换

采用模糊机会约束规划进行建模，并利用三角模糊分布处理式（1）、（6）、（7）和（8）中的模糊参数，从而得到相应的机会约束规划模型：

min F   （15）

s.t.

Pos{F2+F3-F1≤F}≥ξ（16）

Pos{i=jQij}≥b1

（17）

Pos{1iQij=kQjk}≥b2

（18）

Pos{2iQij=mQjm}≥b3

（19）

Pos表示{·}中事件成立的可能性，其中：式（16）反映目標值F在置信水平至少是ξ时所能取得的最小值;式（17）～（19）分别反映约束条件得到满足时的可能性应不小于给定的置信水平b1、b2和b3。

式（15）表示逆向物流网络的总成本最低。为使目标函数表示网络利润最高，可将式（15）转化为：

max（-F）

（20）

定理1 设三角模糊数={ε1，ε2，ε3}，ε1≤ε2≤ε3，则对任意给定的置信水平α（0≤α≤1），当且仅当（1-α）ε1+αε2≤z，（1-α）ε3+αε2≥z时，有Pos{=z}≥α成立。

证明：根据可能性定义Pos{=z}=με（z）可知，若Pos{=z}≥α成立，必有με（z）≥α，则z一定处于的α水平截集[（1-α）ε1+αε2，（1-α）ε3+αε2]内。因此，有（1-α）ε1+αε2≤z，（1-α）ε3+αε2≥z。证毕。

根据定理1，可将式（16）～（19）转化成下列等价形式：

jxj fj+kxk fk+mxmfm+ij（（1-ξ）cj1+ξcj2+dij（（1-ξ）cij1+ξcij2））Qij+jk（（1-ξ）ck1+ξck2+

djk（（1-ξ）cjk1+ξcjk2））Qjk+jm（（1-ξ）cm1+ξcm2+djm（（1-ξ）cjm1+ξcjm2））Qjm+i（（1-ξ）Ri1+ξRi2）（（1-ξ）si1+ξsi2）-jk（（1-ξ）pk1+ξpk2）Qjk+jm（（1-ξ）pm1+ξpm2）Qjm≤F（21）

jQij≥（1-b1）Ri1+b1Ri2（22）

jQij≤（1-b1）Ri3+b1Ri2

（23）

kQjk≥（（1-b2）a11+b2a12）iQij

（24）

kQjk≤（（1-b2）a13+b2a12）iQij

（25）

mQjm≥（（1-b3）a21+b3a22）iQij

（26）

mQjm≤（（1-b3）a23+b3a22）iQij

（27）

2.2 多目标处理

本文所建立的动力电池逆向物流网络模型是一个多目标优化问题。采用加权理想点法对多目标进行处理，可将多目标混合整数规划模型转化为

max WW=ρ（-F）-（-F）*（-F）*-

（1-ρ）Z-Z*Z*

（28）

其约束条件为式（9）～（14）和式（21）～（27）。

式（28）表示使各目标尽可能接近各自的理想值，其中，（-F）*和Z*分别表示将网络利润-F和碳排放量Z作为单一目标所求得的理想解。此外，ρ（0≤ρ≤1）为决策者的偏好系数，由供应链决策者根据实际情况确定。供应链决策者若偏好经济效益则ρ值较大，若偏好环境效益则ρ值较小。

3 算例分析

3.1 算例描述

考虑动力电池回收责任主体建设逆向物流网络，假设逆向物流网络包括13个动力电池更换点、6个收集中心候选点、5个再循环利用中心候选点和5个回收中心候选点。参考文献[8]，并结合调研结果，设置相关成本参数。JEONG等[17]的研究表明，设施建设过程产生的碳排放量为500 kg/m2，本文据此估计设施建设产生的碳排放量。动力电池加工过程产生的碳排放量借鉴MATHUR等[16]和BOYDEN等[18]的研究成果进行计算。根据标准的燃料消耗量和排放量，以汽油為例，每升汽油燃烧平均产生2 320 g二氧化碳，将运输动力电池的油耗转化为碳排放。均匀分布能够随机产生在均值附近波动的参数值，避免数据集中化。本文根据以上调研结果，利用均匀分布随机产生各参数值。逆向物流网络涉及的不确定参数见表1，其他参数见表2。此外，运往再循环利用中心的动力电池比例1的三角模糊数为（0.66，0.72，0.78），运往回收中心的动力电池比例2的三角模糊数为（0.24，0.28，0.32）。

3.2 算例求解

根据相关资料和实际企业应用数据调研结果，设置不确定参数的置信水平ξ=0.9，b1=b2=b3=0.8，并假设决策者对经济效益和环境效益同等重视（偏好系数ρ=0.5，即两个目标函数的权重值相等），利用LINGO软件编程求解得到设施选址结果，见表3。此时，动力电池逆向物流网络利润为4 661.27万元，碳排放量为16 819.87 t，设施间废旧动力电池流向见图2。

3.3 动力电池回收量对逆向物流网络设计的影响

在不确定参数的置信水平ξ=0.9，b1=b2=

b3=0.8，ρ=0.5时，分析废旧动力电池回收量对逆

向物流网络设计的影响，其决策结果见表4。由表4可知：随着动力电池回收比例的增加，收集中心、再循环利用中心和回收中心规模先保持稳定后增大，这与现实相符;回收比例对设施选址影响不大，在回收比例增加时只需扩大现有逆向物流网络的规模，故在动力电池回收比例不稳定的情况下保证运营策略在一定范围内的稳定性即可。此外，由于规模效应，随着动力电池回收比例的增加，逆向物流网络的总利润增加。

3.4 动力电池回收技术对逆向物流网络设计的影响

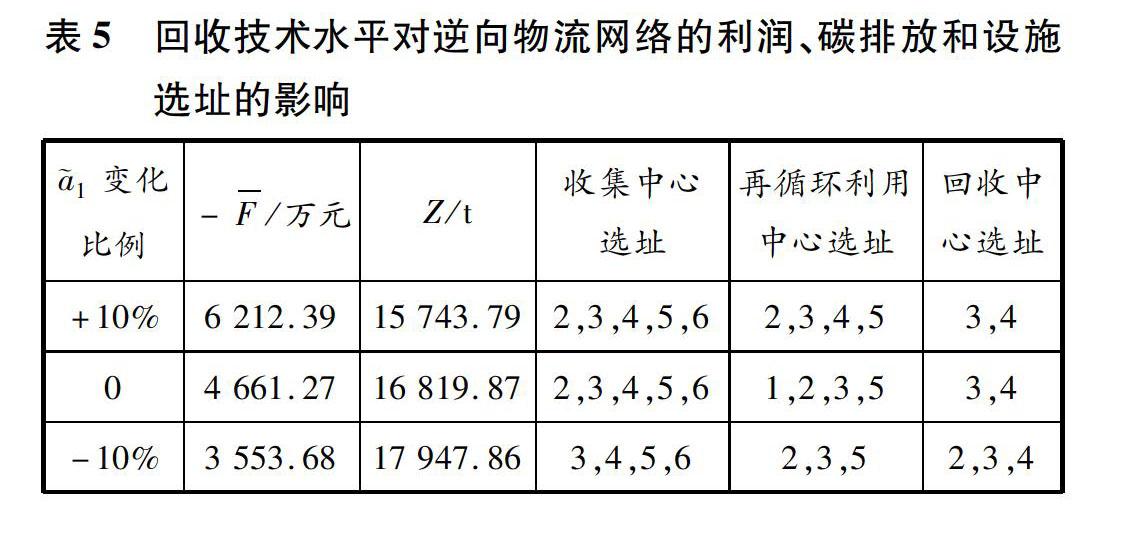
随着动力电池回收技术水平不断提高，电池梯次利用的比例也会提高，即运往再循环利用中心的电池数量增多。将技术水平设置为基本技术水平、高技术水平（适合梯次利用的动力电池比例提高10%）和低技术水平（适合梯次利用的动力电池比例降低10%）等3种等级，其他参数不变。在ξ=0.9，b1=b2=b3=0.8，ρ=0.5时，不同回收技术水平下的动力电池逆向物流网络设计方案见表5。结合表5和图3可以得到以下结论：随着回收技术水平的提高，流入再循环利用中心的动力电池数量增多，而流入回收中心的动力电池数量减少，再循环利用中心规模增大，而回收中心数量减少，收集中心数量发生较小变化;回收技术进步对收集中心、再循环利用中心和回收中心选址影响不大;随着回收技术进步，更多的废旧动力电池流向再循环利用中心，随后被销往梯次利用市场，在实现动力电池使用价值最大化的同时降低了碳排放量，显著提高了逆向物流网络的经济效益和环境效益。

3.5 决策者偏好对逆向物流网络设计的影响

采用加权理想点法处理多个目标，在ξ=0.9，b1=b2=b3=0.8时，对偏好系数ρ进行敏感性分析，研究决策者偏好对动力电池逆向物流网络设计的影响。决策者不同偏好下动力电池逆向物流网络设计方案见表6。在决策者不同偏好下（即不同权重组合下）收集中心选址集中在候选点3、4、5和6，再循环利用中心选址集中在候选点2、3和5，回收中心选址必选候选点3，其次选择候选点1或4，这说明决策者偏好对逆向物流网络选址影响不大，反映了选址方案的稳定性。在此动力电池逆向物流网络设计方案下，若决策者更偏好经济效益，则只需增加收集中心和再循环利用中心的数量。

若决策者对经济效益和环境效益的偏好不同，则逆向物流网络利润和碳排放量变化较大。当决策者只追求经济效益时，网络利润为4 865.55万元;当决策者综合考虑环境效益和经济效益，如ρ=0.4时，网络利润为4 779.72万元，利润虽下降了1.8%，但碳排放量减少了98.16 t。这表明，同时考虑经济效益和环境效益的动力电池逆向物流网络碳排放量少，具有更好的综合效益。

4 结 论

考虑动力电池回收利用市场的不确定性，对动力电池回收利用逆向物流网络进行设计，以网络利润最高和对环境影响最小为目标，建立一个多目标模糊规划模型，确定逆向物流网络设施的选址、数量以及设施间的废旧动力电池流量，并分析回收量、回收技术水平和决策者偏好对动力电池逆向物流网络利润、碳排放和设施选址的影响。结果表明：①随着废旧电池回收比例的增加，设施数量先保持稳定后增加，逆向物流网络利润提高。②回收技术水平影响废旧动力电池回收利用方式，间接影响再循环利用中心和回收中心数量，而收集中心数量不变;动力电池回收技术水平提升，能够提高逆向物流网络利润，减少碳排放量。③决策者的偏好影响动力电池逆向物流网络的利润和碳排放量，决策者选择合适的偏好系数既可以获得较大的经济效益，又可以降低电池回收利用对环境的影响，更有利于实现动力电池逆向物流网络的可持续发展。

参考文献：

[1]ASSUNO A， MOURA P S， ALMEIDA A T D. Technical and economic assessment of the secondary use of repurposed electric vehicle batteries in the residential sector to support solar energy[J]. Applied Energy， 2016， 181： 120-131.

[2]李敬， 杜刚， 殷娟娟. 退役电池回收产业现状及经济性分析[J]. 化工学报， 2020， 71（s1）： 494-500.

[3]张雷， 刘颖琦， 张力， 等. 中国储能产业中动力电池梯次利用的商业价值[J]. 北京理工大学学报（社会科学版）， 2018， 20（6）： 34-44. DOI： 10.15918/j.jbitss1009-3370.2018.5206.

[4]BEER S， GOMEZ T， DALLINGER D， et al. An economic analysis of used electric vehicle batteries integrated into commercial building microgrids[J]. IEEE Transactions on Smart Grid， 2012， 3（1）： 517-525.

[5]劉怡君， 彭频. 循环经济视角下车用动力电池逆向物流链的优化[J]. 江西理工大学学报， 2015， 36（6）： 61-65.

[6]朱广燕， 刘三兵， 海滨， 等. 动力电池回收及梯次利用研究现状[J]. 电源技术， 2015， 39（7）： 1564-1566.

[7]GOVINDAN K， FATTAHI M， KEYVANSHOKOOH E. Supply chain network design under uncertainty： a comprehensive review and future research directions[J]. European Journal of Operational Research， 2017， 263（1）： 108-141.

[8]LI Lin， DABABNEH F， ZHAO Jing. Cost-effective supply chain for electric vehicle battery remanufacturing[J]. Applied Energy， 2018， 226： 277-286.

[9]CHEN Y W， WANG L C， WANG A，et al. A particle swarm approach for optimizing a multi-stage closed loop supply chain for the solar cell industry[J]. Robotics and Computer-Integrated Manufacturing， 2017， 43： 111-123.

[10]程发新， 李莉， 潘婷. 碳税政策下多目标再制造物流网络优化[J]. 工业工程与管理， 2017， 22（5）： 135-141， 149. DOI： 10.19495/j.cnki.1007-5429.2017.05.020.

[11]秦小辉. 不确定环境下独立型废旧家电逆向物流网络优化设计[J]. 统计与决策， 2010（15）： 178-180.

[12]LEE D H， DONG M. Dynamic network design for reverse logistics operations under uncertainty[J]. Transportation Research Part E， 2009， 45（1）： 61-71. DOI： 10.1016/j.tre.2008.08.002.

[13]张群， 卫李蓉. 逆向物流网络设计多目标随机规划模型[J]. 软科学， 2015， 29（10）： 120-124. DOI： 10.13956/j.ss.1001-8409.2015.10.26.

[14]周向红， 成思婕， 成鹏飞. 自营回收模式下再制造逆向物流网络多周期多目标选址规划[J]. 系统工程， 2018， 36（9）： 146-153.

[15]张群， 卫李蓉. 逆向物流网络设计研究进展[J]. 中国管理科学， 2016， 24（9）： 165-176.

[16]MATHUR N， DENG S， SINGH S， et al. Evaluating the environmental benefits of implementing industrial symbiosis to used electric vehicle batteries[C]//26th CIRP Conference on Life Cycle Engineering. Procedia CIRP， 2019， 80： 661-666. DOI： 10.1016/j.procir.2019.01.074.

[17]JEONG Y S， LEE S E， HUH J H. Estimation of CO2 emission of apartment buildings due to major construction materials in the republic of Korea[J]. Energy and Buildings， 2012， 49： 437-442. DOI： 10.1016/j.enbuild.2012.02.041.

[18]BOYDEN A， SOO V K， DOOLAN M. The environmental impacts of recycling portable lithium-ion batteries[C]//23rd CIRP Conferene on Life Cycle Engineering. Procedia CIRP， 2016， 48： 188-193. DOI： 10.1016/j.procir.2016.03.100.

（编辑 贾裙平）