基于递归模糊小波神经网络的INS-GNSS组合导航算法
于仁海 曹春燕 张闯 房美含


摘要:为提高惯性导航系统(inertial navigation system, INS)与全球卫星导航系统(global navigation satellite system, GNSS)相结合的组合导航系统在GNSS中断期间的精度,提出一种基于递归模糊小波神经网络(recurrent fuzzy wavelet neural network,RFWNN)的启发式神经网络结构,用于INS的速度和位置误差补偿。
在GNSS正常工作时,利用INS-GNSS数据将RFWNN训练成一个高精度的预测模型;在GNSS中断期间,利用被训练好的RFWNN模型补偿INS的速度和位置误差。
为对所提出的RFWNN辅助INS-GNSS的性能进行评估,进行实船试验,结果表明利用RFWNN能够有效地对GNSS中断时的速度和位置信息进行高精度修正。
关键词: 惯性导航系统(INS); 全球卫星导航系统(GNSS); 递归模糊小波神经网络(RFWNN)
中图分类号: U666.11
文献标志码: A
收稿日期: 2020-08-31
修回日期: 2020-12-30
基金项目:
国家自然科学基金(51939001,61976033);大连市重点学科重大课题科技创新基金(2018J11CY022)
作者简介:
于仁海(1982—),男,辽宁丹东人,讲师,博士研究生,研究方向为船舶导航,(E-mail)yangaijun@163.com;
曹春燕(1998—),女,江苏南通人,硕士研究生,研究方向为船舶导航,(E-mail)ccy2035@163.com;
张闯(1980—),男,辽宁昌图人,副教授,博士,研究方向为船舶组合导航,(E-mail)zhangchuang@dlmu.edu.cn
INS-GNSS integrated navigation algorithm based on
recurrent fuzzy wavelet neural network
YU Renhai, CAO Chunyan, ZHANG Chuang, FANG Meihan
(Navigation College, Dalian Maritime University, Dalian 116026, Liaoning, China)
Abstract:
To improve the precision of the integrated navigation system that combines the inertial navigation system (INS) and the global navigation satellite system (GNSS) during GNSS interruption, a heuristic neural network structure based on the recurrent fuzzy wavelet neural network (RFWNN) is proposed to compensate the speed and position errors of INS.
The RFWNN is trained into a high-accuracy prediction model by the INS-GNSS data when GNSS works normally, and the speed and position errors of INS are compensated by the trained RFWNN during GNSS interruption.
To evaluate the performance of the proposed RFWNN in INS-GNSS integrated navigation, the real ship tests were executed, and the results show that RFWNN can effectively correct the speed and position information during GNSS interruption.
Key words:
inertial navigation system (INS); global navigation satellite system (GNSS); recurrent fuzzy wavelet neural network (RFWNN)
0 引 言
全球衛星导航系统(global navigation satellite system,GNSS)和微机电系统(micro-electro-mechanical system,MEMS)辅助的惯性导航系统(inertial navigation system,INS)是两种常用的位置和速度信息源。GNSS可以提供三维位置和速度的精确信息,但其性能取决于外部环境和卫星的可见性,在某些环境条件下存在更新率低和信号中断的问题[1]。相反,INS是一种自主系统,通过对陀螺仪和加速度计测得的真实角速率和比力进行连续积分,可以获得位置、速度和方位角信息,但是INS的陀螺仪漂移误差和加速度计偏差会随时间的推移而变大[2]。将INS与GNSS组合(以下将该组合导航系统称为INS-GNSS),可以弥补INS和GNSS各自的缺点,提高导航系统的精度。在INS-GNSS中,卡尔曼滤波(Kalman filter,KF)因其实用性而得到广泛的应用[3]。当GNSS中断导致定位精度严重下降时,INS-GNSS切换到纯INS模式继续导航。然而,纯INS受导航数据误差累积的影响,定位精度会随时间逐步降低,因此INS-GNSS在GNSS中断期间的性能会下降。
基于人工神经网络(artificial neural network,ANN)结构的人工智能(artificial intelligent,AI)机制可以有效改善INS-GNSS的性能,使INS-GNSS在GNSS中断时仍可获得连续可靠的导航信息。当GNSS正常工作时,通过调整神经元之间的连接权值和INS的位置或速度误差,训练ANN来辅助INS-GNSS;经过训练的ANN在GNSS中断时能够补偿纯INS的数据误差。一些将AI技术应用于组合导航领域的研究,与本文最终的应用场景具有联系,近年来的一些AI技术涉及各种输入传感器数据和导航结果。CHIANG等[4]讨论了一种利用多层前馈神经网络与反向传播学习算法融合的INS和差分全球定位系统(differential global position system,DGPS)数据的多传感器集成方法,然而该方法仅提高了位置数据的精度,对速度和航向没有影响。NOURELDIN等[5]提出一种神经元小波算法来整合INS-GNSS的输出数据,并使用KF提供精确的定位数据。SHARAF等[6]研究了位置-位置误差(结构(输入为INS位置,输出为INS与GNSS的位置差),并提出一种径向基函数神经网络模型修正位置(无须处理速度和方位数据的误差)。许哲万等[7]给出一种自适应调整的神经模糊推理结构,以帮助模块进行解算。何康辉等[8]介绍了用于INS-GNSS的动态神经网络,基于当前和过去的一些INS速度和位置样本,使用输入延迟神经网络评估INS的速度和位置误差。CAI等[9]通过反向传播神经网络和递归神经网络组合INS与GNSS,采用了包括反向传播、遗传和粒子群优化在内的常用权重优化算法。此外,为提高函数逼近精度,NOURMOHAMMADI等[10]设计了模糊小波神经网络(wavelet neural networks,WNN)。CHEN等[11]在模糊推理中利用递归WNN以反馈连接的形式提供动態参数。
本文给出一种基于神经网络模型的补偿INS的导航误差框架,并通过应用和速度-速度误差()序列,在GNSS中断期间修正速度和位置数据,进而建立一个神经网络辅助的INS-GNSS。由于神经网络类型的选择对神经网络辅助INS-GNSS的定位精度有重要影响,本文提出一种递归模糊小波神经网络(recurrent fuzzy wavelet neural network,RFWNN)算法,研究神经网络算法的结构及其对误差补偿的影响,并且将本文算法与多层感知器(multilayer perceptron,MLP)、WNN和KF比较,给出估计精度。
1 RFWNN结构
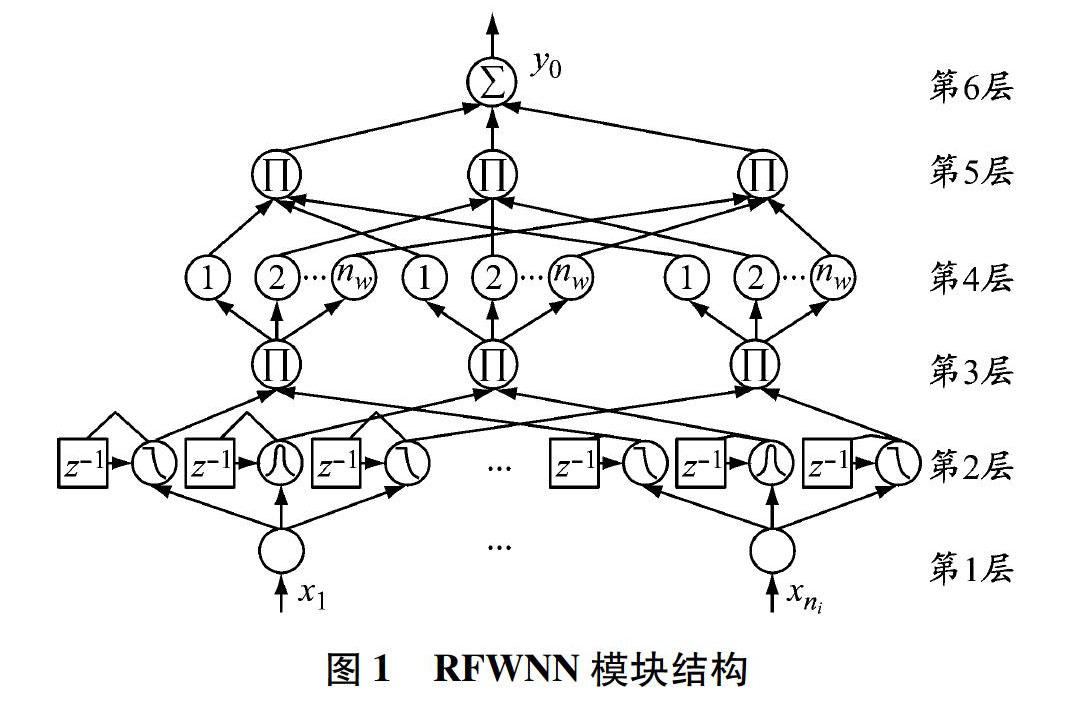
ANN已成为复杂非线性系统建模的一种有效方法,具有强大的计算能力、分类能力和函数逼近能力,适用于对无法用传统算法求解的高度非线性系统和复杂系统进行建模。如果神经元数量和层数足够多,ANN可以将广泛的非线性函数逼近到任何期望的精度[12]。然而,选择合适的ANN结构以及确定神经元参数对神经网络的应用具有重要意义,尤其是在低成本的INS-GNSS中。本文设计了一种RFWNN模块来解决GNSS中断时的位置和速度分量的估计问题。图1给出了RFWNN模块的6层结构,包括输入层、隶属度层、模糊规则层、小波层、小波乘积层和输出层。
(1)第1层为输入层。每个节点i直接向输入层输入信号xi(i=1,2,…,ni)。在输入向量
x=(x1, x2,…, xni)T中,ni表示其维数。
(2)第2层为隶属度层。这层中的神经元表示模糊规则前部分所使用的语言变量的隶属函数。
隶属度层的输入可以表示为
ri,j=xi,n+μi,j,n-1αi,j
式中:n为迭代次数;αi,j为递归反馈连接的权重;μi,j,n-1为高斯隶属函数。第2层的输出信号为
Oj(ri,j)=(ri,j-mi,j)2(si,j)2,
i=1,2,…,ni; j=1,2,…,nj
式中:si,j和mi,j分别为高斯隶属函数的标准差和均值;nj是每个输入信号的语言变量数。网络信息存储于高斯隶属函数中。
(3)第3层为模糊规则层。这层中每个由指定的神经元k(本文中神经元总数为3)都表示一个模糊与运算,与来自第2层的输入信号相乘:
pk=nii=1μi,k(Ok(ri,k)), k=1,2,3
式中:pk表示模糊规则层的第k个输出。
(4)第4层为小波层。在小波层中,来自第3层的每个输入信号pk通过nw个小波节点的激活函数传递。这些激活函数由墨西哥帽小波母函数
(x)给出。
(
x)=(1-
x2)exp(-
x2/2)
式中:
x2=
xT
x。因此,与第3层第k个输入信息相连的第w(w=1,2,…,nw)个小波节点的激活函数如下:
dw,tw(pk)=2dk,w/2(1-2dk,wpk-tk,w2)·
exp(-2dk,wpk-tk,w2/2),w=1,2,…,nw
式中:dw和tw分别为第w个小波节点的伸缩和平移;dk,w和tk,w分别为与第k个输入相连的第w个小波节点的伸缩和平移。
(5)第5层为小波乘积层。与第3层相似,
该层中每个由指定的神经元都表示一个模糊与运算,是第4层的输入信号的乘积:
κp=npi=1dw,tw(pk)
本文中此层的规则数np=nw。
(6)第6层为输出层。在输出层中,每个标量输出为
y0=npp=1wp,0κp
式中:wp,0表示输出与第p个规则之间的连接权重。
参数学习算法用于调整第4层的小波基参数、母小波的伸缩和平移以及输出层的连接权重。该算法基于反向传播技术,目标是利用梯度下降法使成本函数最小化。RFWNN输出与参考值之间的差值根据以下成本函数进行计算:
E=(y0-yd)2/2
(1)
式中:y0和yd分别为RFWNN输出和期望输出。第4层和第6层可调参数的更新律如下:
(1)基于以下步骤构造第4层小波伸缩(dk,w)和平移(tk,w)的更新律:
dk,w,k+1=dk,w,k-ηdEdk,w
tk,w,k+1=tk,w,k-ηtEtk,w
式中:ηd和ηt分别表示小波伸缩和平移的学习率。
(2)基于式(1),第6层连接权重的更新方程如下:
wp,0,k+1=wp,0,k-ηwEwp,0
式中:ηw表示连接权重的学习率。
2 基于RFWNN的INS-GNSS
2.1 组合导航数学模型
惯性状态动力学位置误差模型[13]为
δ=δ
vE(RN+γ)cos β
δ=δ
vNRM+γ
δ=δ
vD
速度误差模型[13]为
δ
E=
2ωsin β+
vERN+γtan β
vN-
2ωcos β+
vERN+γ
vU+fN+fEδh-fDδl+BN
δ
N=-
2ωsin β+
vERN+γtan β
vE-
vNRM+γ
vU+fE+fNδh-fDδL+BE
δ
D=
2ωcos β+
vERN+γ
vE-
v2NRM+γ-g+fD+fEδL-fNδl+BD
姿态误差模型[13]为
δL·=
ωsin β+
vERN+γtan β
l-
ωcos β+
vERN+γ
h+δ
vNRM+γ-
vNδγRM+γ+DN
δl·=-
ωsin β+
vERN+γtan β
L-
vNRM+γh-δ
vERN+γ-
vEδγ(RN+γ)2+ωδβsin β+DE
δh·=
ωcos β+
vERN+γ
L-
vNRM+γl-δ
vERN+γtan β+
vEδγtan β(RN+γ)2-(ωcos β+
vEsec2βRN+γ)δβ+DD
式中:RM和RN分別为子午圈曲率半径和卯酉圈曲率半径;ω为地球自转角速度;g为重力加速度;
vN、vE和vU分别为在向北、向东和向上方向上的速度;fN、fE和fD分别为加速度计输出在向北、向东和向下方向上的比力;BN、BE和BD分别为加速度计在向北、向东和向下方向上的偏差;DN、DE和DD分别为陀螺在向北、向东和向下方向上的常值漂移量。
陀螺常值漂移量和加速度计偏差的一阶马尔科夫模型分别为
D·i=-μDi+ρ
B·i=0 , i=N,E,D
式中:μ为传感器测量的相关系数;ρ为零均值高斯白噪声。
惯性状态动力学误差模型可以用以下状态空间形式[13]表示:
=f(
x,
ρ(t),t)
(2)
式中:f(·)为非线性连续函数;
x为INS的误差状态向量,包括3个位置误差、3个速度误差、3个姿态误差、3个加速度计偏差和3个陀螺常值漂移量;
ρ(t)包括加速度计和陀螺常值漂移的白噪声。
状态向量定义为
x=(δa,δβ,δγ,δ
vN,δ
vE,δ
vD,δL,δl,δh,BN,BE,BD,DN,DE,DD)
式(2)为非线性模型。为将该模型应用于KF,需要对其进行离散化处理[14]:
xk+1=
J(tk+1-tk)
xk+
ρk
(3)
式中:
J是状态转移矩阵;
ρk是与惯性传感器相关的高斯白噪声。同样,量测方程的一般离散形式为
zk=
Hk
xk+
vk
式中:
Hk为观测矩阵;
vk为零均值高斯测量噪声,其协方差矩阵为
R。
zk通过从INS的位置、速度和航向角分别减去GNSS的位置、速度和航向角而实现更新。
Hk=
00000010000000000000001000000000000000100000000010000000000000001000000000000000100000000000-1000000000000
非线性模型式(2)作为神经网络的输入,包括
PINS、
vINS和加速度计输出(
fNED=(fN, fE, fD)T);线性模型式(3)的输出作
为KF的输入;KF用来估计位置误差、速度误差、姿态误差、加速度计偏差和陀螺常值漂移量,然后修正组合系统的最终输出。
2.2 RFWNN辅助的INS-GNSS实现
KF算法具有一些缺陷和局限性,如滤波估计值次优甚至发散[15]。对于低成本INS-GNSS而言,在建立KF线性误差模型时忽略了非线性误差项,导致定位误差较大。因此,本文基于ANN思想实现INS-GNSS的非线性处理。最常用的方法是将INS的误差与输出相关联,预测INS与GNSS输出的差值,而后将其作为KF的观测向量。同样,采用
PINS-δ
PINS和
vINS-δ
vINS结构,将所提出的RFWNN应用于INS-GNSS。RFWNN辅助的INS-GNSS可以在GNSS中断期间连续提供位置和速度误差。将INS的位置、速度和加速度计输出作为RFWNN的输入,而相应的INS的位置误差和速度误差作为RFWNN的输出。图2中:IMU指惯性测量单元(inertial measurement unit),包括陀螺仪和加速度计;
AINS=(L, l, h)T为姿态向量;在RFWNN训练过程中,当GNSS正常工作时,INS和GNSS的输出通过KF进行组合。
如图2所示,对于每个基于MEMS的INS-GNSS而言,如果使用增强KF,
PINS-δ
PINS和
vINS-δ
vINS结构可以得到进一步增强,则可得到在GNSS中断的情况下能提供INS误差和精确定位信息的鲁棒非线性模型。在GNSS可以接收到精确的导航数据时,训练RFWNN将持续减小估计误差,以获得最优的网络因子。用神经网络可以更新突触权值,从而恢复所获得的导航知识。在网络训练模式下,神经网络模块输出的INS位置误差和速度误差应与参考值进行比较。参考速度误差δ
vINS-GNSS和位置误差δ
PINS-GNSS定义为
δ
vINS-GNSS=
vINS-
vGNSS
δPINS-GNSS=
PINS-
PGNSS
RFWNN模块输出的速度误差和位置误差为RFWNN模块的估计误差。为减小这种误差,训练RFWNN对其因子进行修正,并根据最小二乘准则实施更新,直到达到一定的均方误差为止。对所有INS-GNSS信息进行重复训练,直到确定GNSS中断为止。图3给出了GNSS中断期间的RFWNN预测过程。当GNSS发生故障時,GNSS无法提供KF的观测矢量,利用训练好的RFWNN代替GNSS进行导航误差预测。在预测模式中,INS的速度和位置信息以及fNED作为RFWNN的输入,并将包括速度和位置误差信息的神经网络输出融合到KF中。
3 仿真结果与实验分析
3.1 仿真结果
使用实船试验来评估本文所提出的组合导航系统的性能。试验地点为大连港圆岛附近水域,起始点为P1,终点为P2。INS-GNSS导航产生的轨迹见图4。INS生成IMU的原始测量值,以及采样频率为50 Hz的船舶位置、速度和姿态数据,GNSS更新频率为1 Hz。参照基准DGPS接收机,使用实时动态校正可给出高精度的数据,采样频率为100 Hz,采样时间共约1 400 s。在初始状态下,INS-GNSS在初始对准模式下工作200 s。为研究GNSS中断对系统误差的影响,以及检验所提出RFWNN的导航误差预测能力,人为进行GNSS的中断。
3.2 组合导航系统算法性能分析
在GNSS中断期间,RFWNN模块提供速度和位置误差信息替代GNSS数据。4个可访问的神经网络模块包括
P-δ
P结构(用于估计位置(经纬度))和v-δ
v结构(用于估计向北的速度分量(vN)和向东的速度分量(vE))。每个神经网络模块有4个输入层神经元(包括速度或位置分量中的1个以及3个加速度计比力)
和1个输出层神经元(用于提供速度误差和位置误差)。
GNSS第1次中断时间在300 s与360 s之间,船速为10 kn,船舶处于加速状态;GNSS第2次中断时间在600 s与660 s之间,船速为12 kn,船舶处于定速状态。在GNSS第1次中断前,利用从INS和GNSS收集到的测试信息对RFWNN进行训练;而后,利用训练好的RFWNN估计300 s到360 s期间的位置误差和速度误差。图5显示了在GNSS第1次中断前,
P-δ
P模块对船舶位置(经纬度)的训练曲线,目标均方误差为0.000 01。由于
v-δ
v模块的训练过程与
P-δ
P模块的训练过程相似,这里只给出
P-δ
P模块的训练曲线。
为验证该算法的适用性,比较在GNSS中断期间RFWNN辅助的INS-GNSS、GNSS、传统KF对位
置和速度分量的估计结果。应注意的是,在GNSS中断期间,来自GNSS的位置、速度和航向角数据不可靠,因此没有KF的观测矢量。图6和7给出了在GNSS中断期间的位置和速度估计曲线,展示了提出的RFWNN辅助KF算法在位置和速度估计方面的良好性能。结果表明,在GNSS信号中断的情况下,INS误差可以被有效补偿,主要原因是基于神经网络的导航系统可以根据测试航路的训练周期捕获智能信息来减少定位误差。
为验证所提出的RFWNN的有效性,将其与传统的MLP、WNN的性能进行比较。MLP由2个隐藏层和1个四层WNN组成。MLP和WNN的输入和输出与RFWNN相同,并以一个四维向量
作为输入,映射到隐藏层,最后输出一维向量。为更
好地进行估计,表1和2给出了GNSS两次中断期间基于同一组试验数据的位置和速度估计的均值误差和标准差的统计结果。由表1和2可知,与MLP、WNN和KF相比,RFWNN的位置和速度估计的均值误差和标准差明显较低。
4 结 论
基于人工神经网络技术,提出递归模糊小波神经网络(RFWNN)辅助的惯性导航系统(INS)与全球卫星导航系统(GNSS)相结合的组合导航系统(INS-GNSS),通过实船试验对该導航系统的性能进行了评估。该导航系统利用GNSS的位置和速度来辅助INS,在GNSS正常工作时,利用
位置、速度及它们的误差结果辅助INS;在GNSS中断时,利用RFWNN减少INS-GNSS的速度和位置误差累积。当GNSS正常工作时,用INS的速度、位置、比力和GNSS数据等训练RFWNN;在GNSS中断期间,训练的RFWNN将提供精确的位置和速度误差值作为卡尔曼滤波(KF)的观测值,从而减小INS估计误差。试验表明,与多层感知器(MLP)、小波神经网络(WNN)和KF相比,RFWNN辅助的INS-GNSS在GNSS中断期间给出的速度和位置预测误差显
著较低。
参考文献:
[1]段顺利, 孙伟, 吴增林. 抗差自适应EKF在INS/GNSS紧组合中的应用[J]. 电子科技大学学报, 2019, 48(2): 58-62. DOI: 10.3969/j.issn.1001-0548.2019.02.009.
[2]ZHANG Chuang, GUO Chen, ZHANG Daheng. Ship navigation via GPS/IMU/LOG integration using adaptive fission particle filter[J]. Ocean Engineering, 2018, 156: 435-445. DOI: 10.1016/j.oceaneng.2018.03.012.
[3]ISMAIL M, ABDELKAWY E. A hybrid error modeling for MEMS IMU in integrated GPS/INS navigation system[J]. The Journal of Global Positioning Systems, 2018, 16(1): 1-12. DOI: 10.1186/s41 445-018-0016-5.
[4]CHIANG K W, NOURELDIN A, EI-SHEIMY N. Multisensor integration using neuron computing for land-vehicle navigation[J]. GPS Solutions, 2003, 6(4): 209-218. DOI: 10.1007/s10 291-002-0024-4.
[5]NOURELDIN A, OSMAN A, EL-SHEIMY N. A neuro-wavelet method for multi-sensor system integration for vehicular navigation[J]. Measurement Science and Technology, 2004, 51(4): 259-268. DOI: 10.1088/0957-0233/15/2/013.
[6]SHARAF R, NOURELDIN A, OSMAN A, et al. Online INS/GNSS integration with a radial basis function neural network[J]. IEEE Aerospace & Electronic Systems Magazine, 2005, 20(3): 8-14. DOI: 10.1109/MAES.2005.1412121.
[7]许哲万, 李晶皎, 王爱侠, 等. 一种基于改进T-S模糊推理的模糊神经网络学习算法[J]. 计算机科学, 2011(11): 196-199. DOI: 10.3969/j.issn.1002-137X.2011.11.044.
[8]何康辉, 董朝阳, 王青. 一种考虑GPS信号中断的导航滤波算法[J]. 北京航空航天大学学报, 2019, 45(9): 1874-1881. DOI: 10.13700/j.bh.1001-5965.2018.0786.
[9]CAI X, HSU H, CHAI H, et al. Multi-antenna GNSS and INS integrated position and attitude determination without base station for land vehicles[J]. The Journal of Navigation, 2019, 72(2): 342-358. DOI: 10.1017/S037 3463318000681.
[10]NOURMOHAMMADI H, KEIGHBADI J. Fuzzy adaptive integration scheme for low-cost SINS/GPS navigation system[J]. Mechanical Systems and Signal Processing, 2018, 99(15): 434-449. DOI: 10.1016/j.ymssp.2017.06.030.
[11]CHEN S, HUNG Y, HUNG Y, et al. Application of a recurrent wavelet fuzzy-neural network in the positioning control of a magnetic-bearing mechanism[J]. Computer Electrical Engineering, 2016, 54: 147-158. DOI: 10.1016/j.compeleceng.2015.11.022.
[12]CHENG Shou, LI Liang, CHEN Jie. Fusion algorithm design based on adaptive SCKF and integral correction for side-slip angle observation[J]. IEEE Transactions on Industrial Electronics, 2018, 65: 5754-5763. DOI: 10.1109/TIE.2017.2774771.
[13]胡建宇, 侯書铭. UKF在INS/GPS组合导航直接法滤波中的应用[J]. 计算机与数字工程, 2015, 43(2): 252-255. DOI: 10.3969/j.issn1672-9722.2015.02.023.
[14]QUINCHIA A, FALCO G, FALLETTI E, et al. A comparison between different error modelling of MEMS applied to GPS/INS integrated systems[J]. Sensors, 2013, 13: 9549-9588. DOI: 10.3390/s130809549.
[15]LI Jing, SONG Ningfang, YANG Gongliu, et al. Improving positioning accuracy of vehicular navigation system during GPS outages utilizing ensemble learning algorithm[J]. Information Fusion, 2017, 35: 1-10. DOI: 10.1016/j.inffus.2016.08.001.
[16]MAJID M, MOJTABA K, RUPP C, et al. Power production prediction of wind turbines using fusion of MLP and ANFIS networks[J]. IET Renewable Power Generation, 2018, 12(9): 1025-1033. DOI: 10.1049/iet-rpg.2017.0736.
[17]殷礼胜, 唐圣期, 李胜, 等. 基于整合移动平均自回归和遗传粒子群优化小波神经网络组合模型的交通流预测[J]. 电子与信息学报, 2019, 41(9): 2273-2279. DOI: 10.11999/JEIT181073.
(编辑 贾裙平)

