基于博弈论的海上交通事故案例推理方法及应用

闫长健 孙世虎

摘要：为有效积累和挖掘海上交通事故案例蕴含的宝贵经验和知识，提出一种基于博弈论的海上交通事故案例推理方法。从大量海上交通事故历史案例中提取案例特征构建特征指标集，采用偏好比率法和熵值法分别确定指标主觀权重和客观权重，采用博弈论得到综合权重;根据案例特征数据类型，定义不同的指标相似度计算方法，利用灰色关联分析法筛选初始案例组成案例库;结合指标综合权重，构建海上交通事故案例相似度计算模型，进而从案例库中检索出与目标案例相似度最高的案例。通过对海上交通事故应急物资需求的预测，验证了模型的可靠性和适应性，可为海上交通事故发生后的应急决策提供一定的理论参考。

关键词：

海上交通事故; 应急物资; 需求预测; 案例推理; 博弈论

中图分类号：  U698.6

文献标志码：  A

收稿日期： 2020-04-16

修回日期： 2020-06-24

基金项目： 福建省教育厅项目（JT180260）;集美大学李尚大基金（ZC2018006）

作者简介：

闫长健（ 1983—） ，男，河南漯河人，副教授，硕士，研究方向为交通运输系统工程，（E-mail）chjyan@jmu.edu.cn

*通信联系人。（E-mail）sunshihu84@163.com

Case-based reasoning method and application of maritime traffic accidents based on game theory

YAN Changjian1， SUN Shihu2*

（1. Navigation College， Jimei University， Xiamen 361021， Fujian， China;

2. Navigation Branch， Hebei Jiaotong Vocational and Technical College， Tianjin 300381， China）

Abstract：

In order to effectively accumulate and excavate the valuable experience and knowledge contained in maritime traffic accident cases， a case-based reasoning method of maritime traffic accidents based on the game theory is proposed. The characteristic index set is constructed by extracting case characteristics from a large number of historical cases of marine traffic accidents. The subjective and objective weights of indices are determined by the preference ratio method and the entropy value method， respectively， and the game theory are used to obtain the comprehensive weights. According to the case characteristic data types， the different index similarity calculation methods are defined， and the grey correlation analysis method is used to select the initial cases to form a case database. Combined with the index comprehensive weights， a similarity calculation model of marine traffic accident cases is constructed， and then the cases with the highest similarity with the target cases are retrieved from the case database. The reliability and adaptability of the model are verified by forecasting the demand of emergency materials for maritime traffic accidents. The proposed method can provide theoretical reference for emergency decision-making after maritime traffic accidents.

Key words：

maritime traffic accident; emergency material; demand forecast; case-based reasoning; game theory

0 引 言

近年来，随着经济全球化发展以及“一带一路”倡议的提出，海上船舶往来更加频繁，船舶密度加大，发生海上交通事故的风险增大[1]。2017年8月1日，一艘载有约1 420 t货物的货船在长江白茆沙北水道水域沉没，共造成6人死亡和2人失踪。2019年10月8日，一艘名为“粤阳坡0158”的渔船在珠海横琴岛海域沉没，共造成3人遇险和2人失踪[2]。海上事故发生后，为减少人员伤亡和最大化减小事故带来的损失，需要迅速展开海上搜救。对大量海上交通事故案例信息进行挖掘，对提升海上搜救效率具有十分重要的意义。目前，部分学者基于历史事故案例构建相应的案例库，将挖掘出的事故信息用于总结事故处置方法及制定预防措施等，其中：李华[3]基于海上油田积累的历史数据资源，开发了事故案例库系统;薛金凯[4]在对海上搜救决策过程进行充分研究的基础上，设计基于案例推理的海上搜救辅助决策模型，并在JADE平台实现了该辅助决策系统;秦霜霜等[5]基于全球范围内300多起典型火灾事故案例，构建完整的火灾事故案例库，用于挖掘历史事故案例信息，总结火灾事故的处置方法和预防措施。基于构建的海上交通事故案例库，深入挖掘事故信息，用于应急救援等行动，而对海上事故进行应急救援的前提是应急物资需求预测。因此，基于构建的案例库模型实现海上交通事故应急物资需求预测具有十分重要的意义。对应急物资需求进行预测的方法主要有BP神经网络[6]、模糊粗糙集理论[7]、多元回归分析法[8]等。部分学者将案例推理方法应用到应急物资需求预测方面：LIU等[9]为解决应急物资储备和配置问题，针对应急物资需求预测的特点，利用案例推理方法对地震灾害应急物资需求进行预测;WANG 等[10]利用改进的案例推理规则对地震后应急物资需求进行预测，并通过与灰色关联分析法比较证明案例推理模型的优越性;张文芬等[11]和邓守城等[12]根据水上交通事故的特征属性，构建了水上突发事件应急物资需求模型，间接地预测了水上突发事故应急物资需求量。然而，目前对海上交通事故案例库构建以及基于数据挖掘对海上突发事件应急物资需求预测的研究都较少，并且现有案例检索方法很少考虑指标属性的模糊信息，在权重的确定上多依赖人的主观判断。

基于此，本文在大量海上交通事故历史案例中提取案例特征构建特征指标集，采用博弈论确定指标综合权重，利用灰色关联分析法对现有案例进行初步筛选进而构建新的案例集;构建海上交通事故案例相似度计算模型，进而从案例库中检索出与目标案例相似度最高的案例。通过对海上交通事故应急物资需求量的预测，验证模型的可靠性和适应性，为海上事故发生后的应急决策提供一定的理论参考。

1 案例推理相关理论

案例推理技术是人工智能领域非常重要的一项推理技术，是人们根据历史经验解决现有问题的一种方法或技术[13]。

案例推理的工作机理为：首先对目标案例及其属性进行描述，然后根据规则推理及案例推理的4R （retrieve、reuse、revise、retain）循环模型，从历史案例库中初步筛选出与目标案例相似的历史案例集;从相似案例集中选出与目标案例最相似的案例，对比新旧案例，对最相似的案例的应急物资需求进行微调，从而推理出目标案例的应急物资需求预测结果。基于案例推理的海上交通事故应急物资需求预测实现过程见图1。

2 海上交通事故案例相似度计算模型构建

2.1 案例的表示

海上交通事故特征包含事故类型、事故规模等级、船舶载货情况、遇险人员的数量和伤亡情况以及海上事故现场的水文气象条件等[12，14]。在参考相关文献及咨询相关专家的基础上，总结出12个海上交通事故特征（即指标），具体见表1。根据交通运输部于2014年9月30日发布的《水上交通事故统计办法》，水上交通事故类型主要包括碰撞事故、搁浅事故、触礁事故、触损事故、浪损事故、火灾爆炸事故等;应急响应级别根据《水路交通突发事件应急预案》，按其性质、严重程度、可控性和影响范围等，由高到低分为Ⅰ级（特别重大）、Ⅱ级（重大）、Ⅲ级（较大）和Ⅳ级（一般）等4级;船舶类型主要有客船、集装箱船、散货船、油船、滚装船等。

通过对现有海上交通事故历史案例的统计分析，挖掘案例信息，构建海上交通事故案例库。案例库一般由3部分组成：

S={A，B，D}

（1）

式中：A为历史案例集，A={A1，A2，…，An};B为特征集（也称为指标集），B={B1，B2，…，Bm};D为目标案例。记特征权重为ω=（ω1，ω2，…，ωm），满足mj=1ωj=1。根据目标案例D构造特征矩阵P=（Pij）n×m，其中Pij为第i个案例的第j个特征值。

2.2 特征相似度确定

海上交通事故特征数据主要有3种：符号型，通过准确的文字表达事件特征，如事故类型;数值型，采用数值对事件特征进行准确表达，如风速;描述型，用来描述难以用准确的文字和具体的数值表达的态度特征[15]，如应急响应级别。

采用不同计算方法，对上述3种特征数据进行相似度计算。

（1）符号型。该类型的特征值可逐一列举说明，且特征值之间不存在大小对比关系。因此，可对符号型特征的相似度做如下判定：若目标案例D与历史案例Ai的特征值相同，则界定两者之间的相似度为1，否则相似度为0。

S（aj，cj）=1， aj=cj

0， aj≠cj

（2）

式中：aj和cj分别为历史案例Ai和目标案例D的第j个特征值，j=1，2，…，m。

（2）数值型。对实质性不同的特征数据，采用略微更改的曼哈顿距离进行计算：

D（aj，cj）=aj-cjmax{aj}-min{aj}

（3）

式中：max{aj}和min{aj}分别为历史案例第j个特征值的最大值和最小值，j=1，2，…，m。因此，数值型特征的相似度计算公式为

S（aj，cj）=1-D（aj，cj）

（4）

（3）描述型。针对模糊型案例特征，采用隶属函数計算其相似度：

S（aj，cj）=S（aj∩cj）S（aj）+S（cj）-S（aj∩cj）

（5）

2.3 基于博弈论的指标综合权重确定

指标权重大小反映了指标在案例相似度评估中的相对重要程度，一般情况下指标权重越大对案例检索结果的影响就越大，因此权重分配的合理与否直接影响到案例检索的精确性和准确性。而博弈论是一种通过多个决策主体的决策均衡来实现各方利益最大化的方法，该方法结合了主、客观赋权法各自的优点，既能考虑实际数据特点又能够参考决策者意见，使指标赋权实现了主观与客观的统一，在多属性决策问题上得到广泛应用并取得了不错的效果。因此，为避免传统的案例推理方法指标权重确定过于主观的问题，本文在加法集成法、乘法集成法等综合集成方法的基础上，提出一种更为科学合理的综合权重确定方法，即采用偏好比率法和熵值法分别确定指标主观权重和客观权重，然后采用博弈论[16]得到综合权重。

2.3.1 偏好比率法

偏好比率法[17]是对指标的重要程度进行主观评价的一种方法。由此，可以主观定义两个指标间相对重要程度的大小，得到指标间的偏好比率标度，见表2。

将m个指标B1，B2，…，Bm进行主观排序，两两比较得出偏好比率值bi，j，建立方程组如下：

b1，1ω1，1+b1，2ω1，2+…+b1，mω1，m=mω1，1

b2，2ω1，2+b2，3ω1，3+…+b2，mω1，m=（m-1）ω1，2

…

bm-1，m-1ω1，m-1+bm-1，mω1，m=2ω1，m-1

ω1，1+ω1，2+…+ω1，m=1

（6）

求解上述方程组得到主观权重ω1=（ω1，1，ω1，2，…，ω1，m）。

2.3.2 熵值法

熵值法是通过计算熵值判断数据中某个特征属性的离散程度，从而确定指标权重的一种客观赋权法[18]。根据熵值法的特点，一般数据中信息越多，信息量就越大，其不确定性就越小，熵值就越小。

记n个案例的m个指标的原始值组成的矩阵为A=（aij）n×m。熵值法确定指标权重的步骤如下：

（1）指标标准化处理：

a*ij=aij-min aijmax aij-min aij（7）

（2）依据标准化决策矩阵，求得第j个指标的熵值：

ej=-1ln mni=1（pijln pij）

（8）

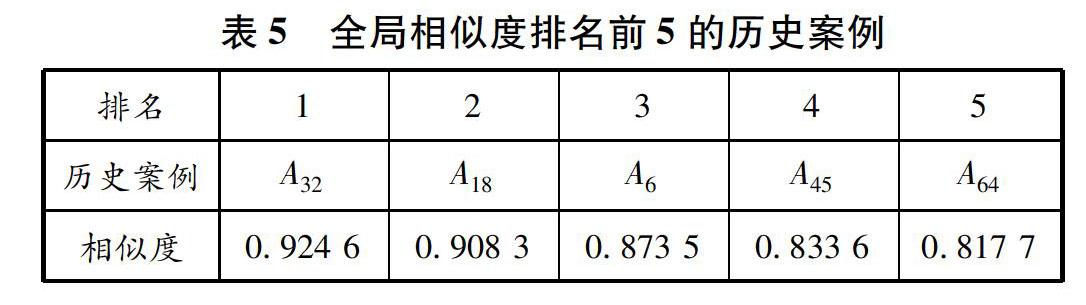
式中：pij=a*ijni=1a*ij，0

（3）求第j个指标的差异系数：

dj=1-ej

（9）

（4）求第j个指标的熵权重ω2=（ω2，1，ω2，2，…，ω2，m）：

ω2，j=djmj=1dj

（10）

2.3.3 基于博弈论确定指标综合权重

对求得的2个权重向量ω1和ω2进行线性组合，得到ω=aω1+bω2。基于最优策略，对ω进行离差极小化处理。归一化处理后，得到最优权重系数a*和b*，故综合最优权重为

ω*=a*ω1+b*ω2

（11）

2.4 灰色关联分析法筛选初始案例集

由于历史案例库中存在一部分相似度较低的案例，故要从中初步筛选出相似度较高的案例构成新的案例库，以便后期精确、高效地检索出与目标案例最匹配的案例。灰色关联分析法是一种计算系统内个体间相似度的方法，具有简单快捷、适用范围广的特点，因此本文采用灰色关联分析法[19]对现有案例进行初步筛选。

根据灰色关联分析法，目标案例D与现有案例Ai的任一特征的关联系数的计算公式为

ξi（k）=miniminky（k）-xi（k）+ρmaximaxky（k）-xi（k）y（k）-xi（k）+ρmaximaxky（k）-xi（k）

式中：ρ为分辨系数，通常取0.5;{y（k）}为参考序列，又称母序列;{xi（k）}为比较序列，又称子序列。从而，目标案例D与历史案例Ai的关联度为

ri=1nnk=1ξi（k）

2.5 全局相似度计算

历史案例Ai与目标案例D之间的相似度为

L（Ai，D）=mj=1（ω2ja′jc′j）mj=1（ω2ja2j）mj=1（ω2jc2j）

（12）

式中：a′j和c′j分别为历史案例Ai和目标案例D的第j个特征值标准化后的值。

2.6 案例学习与调整

通过以上分析，最终匹配到案例库中与目标案例相似度最大的案例。结合目标案例的实际情况及相关需求，对检索出的案例进行学习与调整，从而实现对海上交通事故应急物资需求量的预测。

3 算例分析

假设我国某水域发生一起碰撞事故，船舶类型为散货船，载有船员14人，船舶发生轻微破损，事故共造成10人落水、2人受伤，应急响应级别为Ⅲ级，船龄为9 a，事故发生时能见度为2 km，风速为2 m/s，流速为3 m/s。现有案例库中有320个案例，通过灰色关联分析法，以0.6为相似度阈值，从320个案例中初步筛选出67个符合条件的相似案例，构成新的案例库。筛选出的历史案例和目标案例D的指标数据见表3。

3.1 基于博弈论确定指标综合权重

根据海上交通事故的特点对指标重要程度进行排序：B2B3B4B7B5B8B6B1B9B10B12B11。将根据表2得到的偏好比率值代入式（6）建立方程组并求解得到指标主观权重ω1=（0.056，0.178，0.152，0.147，0.095，0.057，0.112，0.068，0.048，0.039，0.022，0.026）。

从初步筛选出的67个相似案例中随机选取10个案例，将这10个案例的原始数据转化为标准数据，利用熵值法得到客观权重ω2=（0.033，0.193，0.210，0.121，0.076，0.063，0.090，0.066，0.041，

0.042，0.035，0.029）。

利用博弈论建立最优组合系数方程组：

aω1ωT1+bω1ωT2=ω1ωT1

aω2ωT1+bω2ωT2=ω2ωT2

求解得到a=0.572，b=0.543，归一化处理后得到a*=0.513，b*=0.487。根据式（11）得到综合指标权重，ω=（0.045，0.185，0.180，0.134，0.086，0.060，0.101，0.067，0.045，0.040，0.028，0.027）。

3.2 案例相似度计算和案例匹配

在12個指标中，事故类型B1、船舶类型B6、货物类型B9为符号型指标，应急响应级别B2和船舶破损程度B7为描述型指标，其他的都为数值型指标。利用第2.2节的方法对不同类型的指标进行特征相似度确定，得到筛选出的历史案例与目标案例的特征相似度，见表4。

利用式（12）和MATLAB编程计算得到目标案例与历史案例的全局相似度。选取全局相似度排名前5的历史案例（见表5）进行分析。相似度最高的历史案例为A32，其次为A18。如果将相似度阈值设为0.9，则A32和A18都为最佳相似案例，A32相似度更高。目标案例D中散货船在运输过程中发生船舶碰撞事故，造成少量的人员落水和人员伤亡。虽然案例A32与案例A18的事故类型、流速、能见度等不同，但是同样发生了少量的人员落水和失踪险情，并且案例A32需要搜救的人数与目标案例的更接近（都为1人），因此，目标案例D与历史案例A32具有相似的救援方式及应急物资需求。

3.3 案例学习与调整

通过案例推理发现，虽然历史案例A32与目标案例D具有相似的救援方式及应急物资需求，但是两者并不完全一样。根据案例推理相关理论及原则，将目标案例和最佳匹配案例的相关信息给领域专家，领域专家根据目标案例实际情况，对最佳匹配案例的应急物资需求进行调整和修正，作为目标案例应急物资需求预测的结果，从而实现对海上交通事故应急物资需求量的预测。

此外，对案例进行修正需要对案例进行分析与推理，在此过程中也会积累相关的知识和经验。将这些修正方案及其对应的应急物资需求结果作为一个新案例保存到案例库中，可促使模型算法不断学习与成长。因此，通过案例学习，不仅能够不断增加案例库容量，而且能够在一定程度上提高模型的适应性。

4 结束语

为深入挖掘和利用海上交通事故案例蕴含的宝贵知识，从大量海上交通事故历史案例中提取案例特征构建特征指标集，并对不同类型指标采用不同方法进行数值化处理，构建了海上交通事故案例库。利用博弈论计算综合指标权重，利用灰色关联分析法对现有案例进行初步筛选构建新的案例集，然后通过案例推理模型检索出与目标案例相似度最高的案例。根据目标案例实际情况对相似度最高的案例进行调整和修正。通过对海上交通事故应急物资需求量的预测验证了模型的可行性和适用性。本文提出的案例库及检索方法克服了指标权重确定不合理的问题，提高了海上交通事故应急物资需求预测的精度，具有一定的科学性，能够在海上交通事故发生后为决策部门提供较为有效、可靠的决策依据。

参考文献：

[1]涂敏， 胡远程. 船舶海上碰撞事故影响因素分析[J]. 物流技术， 2018， 37（2）： 53-66， 72. DOI： 10.3969/j.issn.1005-152X.2018.02.012.

[2]中华人民共和国广东海事局. 珠海：“粤阳坡0158”渔船沉没， 船上3人遇险， 1人获救[EB/OL]. （2019-10-14）[2020-06-20]. https：//www.gd.msa.gov.cn/gd/ShowArticle.asp？ArticleID=37028.

[3]李华. 海上油田复杂情况与事故案例库系统的开发及应用[J]. 石化技术， 2018， 25（8）： 140.

[4]薛金凯. 基于案例推理的海上搜救辅助决策研究[D]. 大连： 大连海事大学， 2011.

[5]秦霜霜， 吕伟， 余惠琴， 等. 基于案例推理的火灾事故相似度及应对措施研究[J]. 安全与环境工程， 2018， 25（5）： 150-155. DOI： 10.13578/j.cnki.issn.1671-1556.2018.05.023.

[6]钱枫林， 崔健. BP神经网络模型在应急需求预测中的应用： 以地震伤亡人数预测为例[J]. 中国安全科学学报， 2013， 23（4）： 21-26. DOI： 10.16265/j.cnki.issn1003-3033.2013.04.017.

[7]SUN Bingzhen， MA Weimin， ZHAO Haiyan. A fuzzy rough set approach to emergency material demand prediction over two universes[J]. Applied Mathematical Modelling， 2013， 37（10/11）： 7062-7070. DOI： 10.1016/j.apm.2013.02.008.

[8]GU Yong， CHEN Ping. Analysis of reserve demand for regional emergency materials[C]//International Workshop on Intelligent Systems & Applications. IEEE， 2011. DOI： 10.1109/ISA.2011.5873426.

[9]LIU Wenmao， HU Guangyu， LI Jianfeng. Emergency resources demand prediction using case-based reasoning[J]. Safety Science， 2012， 50（3）： 530-534. DOI： 10.1016/j.ssci.2011.11.007.

[10]WANG Xiaobo， SUN Ping， YANG Yan， et al. A prediction model of emergency material demand based on case-based reasoning[C]//Control & Decision Conference. IEEE， 2016. DOI： 10.1109/CCDC.2016.7532074.

[11]张文芬， 杨家其. 基于小波神经网络的海上突发事件应急资源动态需求预测[J]. 运筹与管理， 2015， 24（4）： 198-205.

[12]邓守城， 吴青， 石兵， 等. 基于案例推理的水上交通突发事件应急响应资源需求预测[J]. 中国安全科学学报， 2014， 24（3）： 79-84. DOI： 10.16265/j.cnki.issn1003-3033.2014.03.013.

[13]KOLODNER J L. An introduction to case-based reasoning[J]. Artificial Intelligence Review， 1992， 6（1）： 3-34.

[14]汪飞翔， 杨亚东， 田书冰， 等. 基于SVM的水上交通事故严重程度的影响因素研究[J]. 交通信息与安全， 2018， 36（2）： 18-32. DOI： 10.3963/j.issn.1674-4861.2018.02003.

[15]谢健民， 秦琴， 吴文晓. 基于本体的突发事件网络舆情案例推理模型[J]. 情報杂志， 2019， 38（1）： 83-90. DOI： 10.3969/j.issn.1002-1965.2019.01.014.

[16]王会东， 何世繁， 潘晓宏， 等. 基于博弈论权重集化模型的多属性群决策VIKOR方法[J]. 统计与决策， 2019， 35（4）： 39-43. DOI： 10.13546/j.cnki.tjyjc.2019.15.008.

[17]张以晨， 佴磊， 孟凡奇， 等. 基于最优组合赋权理论的可拓学评价模型的应用[J]. 吉林大学学报（地球科学版）， 2011， 41（4）： 161-166， 186.

[18]邬惠国， 刘春姣， 肖英杰. 基于格序决策理论的LNG船舶进出港组织方案比选[J]. 上海海事大学学报， 2012， 33（2）： 10-13.

[19]牛佳伟， 李连博， 陈昌源， 等. 加权灰色关联理论模型在辽宁海上交通事故分析与预测中的应用[J]. 上海海事大学学报， 2016， 37（1）： 65-69， 102. DOI： 10.13340/j.jsmu.2016.01.012.

（编辑 赵勉）