基于粒子群改进的高铁隧道沉降预测研究
年刚伟 季北 张安俊

摘 要:高铁隧道的建设是高铁建设的重要一部分,大量的隧道建设会引起地表沉降。对沉降实测数据进行分析,得出隧道在沉降方面的长期沉降规律,可以实现隧道沉降预测,从而推进的隧道的安全、高速建设。本文针对高铁隧道沉降预测问题,运用粒子群算法(PSO) 对灰色模型GM(1.1 ) 进行改进,构建了灰色-时序组合模型对问题进行了预测研究。研究表明,基于粒子群改进的灰色-时序组合模型对高铁隧道的沉降预测具有实际意义,它能够更好地预测高铁隧道沉降趋势。
关键词:隧道沉降预测;粒子群算法;灰色模型
中图分类号:U457 文献标识码:A 文章编号:1001-5922(2021)06-0165-04
Abstract:High-speed railway tunnel construction is an important part of high-speed railway construction, a large number of tunnel construction will cause surface subsidence. Through the analysis of the measured settlement data, the long-term settlement law of the tunnel in settlement can be obtained, and the prediction of the tunnel settlement can be realized, so as to promote the safe and high-speed construction of the tunnel. Aiming at the settlement prediction of high-speed railway tunnel, particle swarm optimization (PSO) is used to improve the grey model GM (1.1) , and a grey-time series combination model is constructed to predict the problem. The results show that the grey-time series combined model based on particle sswarms has practical significance for the settlement prediction of high-speed railway tunnels, and it can better predict the settlement trend of high-speed railway tunnels.
Key words:tunnel settlement prediction; particle swarm optimization algorithm; grey model
高铁是世界步入铁路运输现代化的重要标志,它的出现带动了国家经济的发展,加速了经济全球化。随着高铁在全国的大面积建设,相应的高铁隧道的建设工作也在有条不紊的进行。由于高铁隧道施工现场复杂且受多种因素影响,因此为保障施工安全,必须重视对高铁隧道的变形预测。
高铁隧道的挖掘过程中,必定会导致地表下沉,预测高铁隧道沉降趋势有利于不断推进工程进度以及施工安全工作的开展。不同的预测方法,对高铁隧道沉降的预测精度有所差别,本文在粒子群算法的基础上,利用小波去噪以及组建灰色-时序组合模型对隧道沉降进行了预测。最后,通过对模型进行模拟拟合和预测精度对比分析,证明基于粒子群改进的GM(1,1)-AR(1)组合模型的在预测高铁隧道沉降时,预测精度最高,能更好的预测隧道沉降趋势。
1 PSO-GM(1,1)简介
传统GM(1,1)模型建立过程中,模型背景值的选取定位为,其中。然而实际中的背景值,它的定义是。由此可知,模型的背景值与实际的背景值存在一定的误差。下图为模型背景值的误差图,曲边梯形面积为实际背景值模型,梯形面积为传统灰色模型。
研究认为,a和u是影响背景值的重要参数,因此,为使模型预测结果更加精确,通过粒子群算法对两个参数进行优化,并对背景值的构造进行了改进。
(1)对背景值的构造改进如下:
(2)對a、u两个背景值参数的优化改进如下:
设置N个粒子初始位置和速度,并计算出它们的适应度函数为均方根误差,得到式子:
式中,为PSO-GM(1,1)模型的拟合值,为建模序列。
2 PSO-GM(1,1)模型改进
虽然利用粒子群算法对GM(1,1)模型进行了改进优化,得到了组合模型PSO-GM(1,1),但由于该组合模型的随预测时间增加,预测精度会降低,因此本文引入等维递补灰色模型,进一步提高模型预测精度。
2.1 PSO-等维递补GM(1,1)组合模型
等维递补即去掉第一期样本数据,将每次预测的第一个值当做下一次预测的样本。PSO-等维递补GM(1,1)模型即基于粒子群算法(PSO)的GM(1,1)模型,通过等维递补的方式与时间序列模型的组合模型,具体为:
设定一个预测值,得到序列:
去掉,得到序列:
以此类推。
2.2 灰色-时序组合模型
灰色GM(1,1)模型预测公式为,当时,
为模型的预测值。时间序列AR模型预测公式为,令t=t+l,则预测的递推公式为:
为区分GM(1,1)模型与AR序列模型,这里替换AR序列模型的x为,则其递推预测公式为:
3 基于改进组合模型的高铁隧道沉降预测研究
由于高铁隧道施工环境复杂,为有效获取隧道沉降监测信息,本文采用小波去噪的方法对隧道沉降进行监测。小波即指小的波形,由于它能很好地分析并提取分平稳信号中的局部信号,因此在现代分析中常作为有效的分析工具。利用小波对沉降数据进行去噪处理,可以很好地保留数据的有用部分。
3.1 小波去噪处理原始沉降数据
3.1.1 小波去噪原理
小波去噪原理即通过小波变换对信号中所含有的有用信息和噪声时频特征进行判断,筛选出有用信息去除噪声。以下为利用小波变换进行信号去噪的步骤:
步骤1:小波分解。在进行小波去噪的处理前,需要对原始信号进行分解,并获取需要的低频信号。
步骤2:阈值处理。小波进行分解高频系数中,通过设定不同的阈值可以提取不同量的真实信号,合适的阈值能有效避免真实信息被当做噪声去掉。
步骤3:小波重构。将分解后得到的低频信号与阈值得到的高频信号重新组合,重构得到新的信号。
设一段含有高斯白噪声的信号的j时刻小波变换系数为,则。式中,表示被污染的信号,表示初始信号的小波变换系数,表示噪声级,表示高斯白噪声。其中为常数且大于零,服从正态分布。
若想将被污染的信号恢复成初始信号,需确定小波分解层数,然后进行硬阈值法和软阈值法去噪。其中,硬阈值法公式如下:
软阈值法公式如下:
当有N个离散点时,定义,当时,则表示保留的小波系数,表示小波在进行逆变换后得到的原始信号估计值。
3.1.2 小波去噪精度评定
小波去噪精度评定即小波去噪效果好坏的判定,在判定中通常采用不同的指标进行评价,如SNR、MSE、PSNR、GSNR等。
式中,x表示原始序列,表示变换后的数据序列。
式中,表示信噪比,N表示信号序列中的数量,ps表示变形信号的功率,pn表示噪声信号的功率。
峰值信噪比:
式中,峰值信噪比指最大功率与信噪比的比值,其值越大则降噪性能越好。
信噪比增益:
式中,信噪比增益表示原始信号去噪前后的信噪比比值,其值越大则降噪效果越好。
3.1.3 小波分析去噪及结果分析
由于高铁隧道沉降数据稳定性差,因此其小波函数的范围较广,而小波函数的选择是影响小波去噪结果的重要因素,所以需要对其小波函数进行筛选。为更好地研究分析高铁沉降数据,本文选择Db4小波进行相应数据处理。在对数据进行分析之时,首先需要对小波进行分解。过少的分解会留下多余的数据,影响去噪的精度;过多的分解会过滤掉有用的信息。通过相应的实验,本文设定对数据的分解层数为2~3层,并采用自适应阈值和自适应软阈值法分析阈值对去噪结果精度。
其中分解层数对去噪精度影响的结果如表1所示,阈值对去噪精度影响的结果如表2所示。
由表可知,3层分解层数去噪后的的信噪比比2层分解层数去噪后的信噪比小,软阈值去噪后的信噪比比硬阈值去噪后的信噪比小,可见在分析高铁隧道沉降数据时,2层分解层数的去噪效果比3层分解层数的去噪效果好,软阈值去噪的效果比硬阈值的去噪效果好。
4 组合模型预测结果
4.1 粒子群寻优结果分析
设定粒子群规模为9,最大代数为100,c1、c2为2,惯性因子W=0.6,待优化的参数在0-1之间,则通过粒子群算法进行迭代寻优的计算过程如图2所示。
图2、3、4是不同迭代数的粒子群寻优图。由图可知,第一幅迭代图的适应值为0.223且保持平稳不变,第二幅和第三幅迭代图的适应值在0.2左右,因此可以說明在迭代过程中,粒子群算法容易陷入局部最优解。
4.2 基于粒子群的灰色-时序组合模拟预测分析
通过对粒子群算法寻优迭代图分析发现,在进化代数大概在30次后,这时的适应度值已经稳定,优化后的模型背景值为0.512。
由此可得到其PSO-GM(1,1) 拟合残差,具体如表3所示。
设定模型小概率误差P=1,后验差比值C=0.071,由此可以得出。通过零均值化对数据进行建模,得到样本偏自相关函数以及ATCC数值,进而推算出组合模型预测结果为-19.86mm。
4.3 模拟拟合及预测精度对比分析
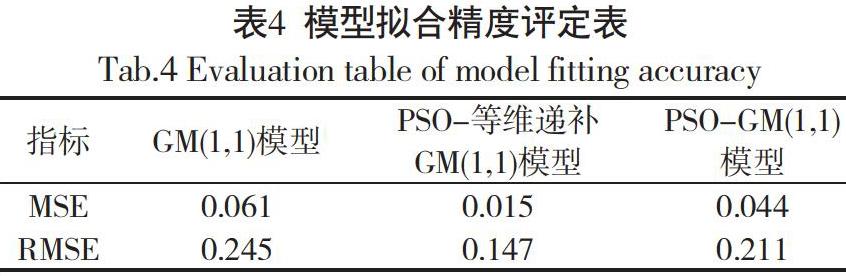
对灰色GM(1,1)模型和PSO-GM(1,1)模型的拟合及预测精准度进行对比分析,可得到如表4所示的结果。
由表4可知,基于粒子群算法的GM(1,1)模型的拟合结果均方误差(MSE)和均方根误差(RMSE)都比原始灰色GM(1,1)值要小,可见基于粒子群算法的GM(1,1)拟合精度更高。
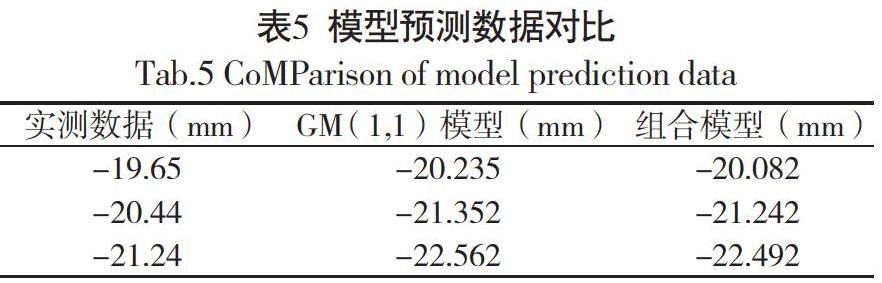
针对单一模型和组合模型预测精度情况,本文从通过实际建模对问题进行了分析,得到如表5所示的预测结果。
由结果可知,组合模型GM(1,1)-AR(1)预测结果高于单一模型GM(1,1)。
5 结语
高铁隧道施工环境复杂,有效的沉降预测有利于保证施工过程的安全。本文针对高铁隧道沉降预测问题,首先利用小波去噪初步处理原始数据进行处理,并在粒子群算法的基础上通过改进的灰色-时序组合模型对隧道沉降进行了预测。在进行小波去噪处理过程中,通过比较硬阈值去噪法和软阈值去噪法以及2层分解层数和3层分解层数初步处理了数据。经过精度分析评定得出结论,2层分解层数和采用软阈值法处理后的数据去噪效果更好。最后,在粒子群算法的基础上提出灰色-时序组合模型,并通过对模型的预测分析,结果证明,GM(1,1)-AR(1)组合模型的预测精度比单一模型的预测精度更好。
参考文献
[1]刘文生,权文斌.基于改进等维信息灰色模型的高铁隧道沉降预测研究[J].测绘与空间地理信息,2018,41(06):210-213.
[2]林先俊.基于物联网模式的自动化沉降监测系统在高铁隧道监测中的应用[J].郑铁科技,2019(04):31-34.
[3]毕旋旋,任超,邓开元,等.小波-ARIMA模型在贵广高铁隧道沉降预测中的应用[J].桂林理工大学学报,2020,40(01):156-160.

