基于信息分解条件的滑坡变形预测

赵 淑 敏

(陕西铁路工程职业技术学院 工程管理与物流学院, 陕西 渭南 714000)

滑坡是中国常见的地质灾害之一，其分布范围较广，对区内居民的生命财产安全造成了严重威胁；同时，由于滑坡变形是其稳定性的直观体现，使得开展滑坡变形预测研究具有重要意义[1-2]。值得指出的是，在滑坡变形监测过程中，受监测环境条件限制，滑坡变形数据会含有一定的误差信息，其会对变形预测分析结果造成一定影响，进而有必要在滑坡变形预测过程中进行变形数据的信息分解处理，且栗燊等[3]探讨了不同去噪方法在滑坡变形数据误差信息剔除过程中的适用性；陆付民等[4]则利用卡尔曼滤波实现了滑坡变形信息分解，上述研究虽为滑坡变形信息分解提供了一种思路，但均未涉及经验模型方法的应用研究。同时，在滑坡变形预测过程中，王鸣等[5]利用指数平滑方法实现了滑坡变形预测，而黄晓虎等[6]则在多类阈值条件构建基础上，实现了滑坡变形预测，上述研究虽取得了相应成果，但均是利用单一模型进行预测研究，也缺乏预测结果的准确性校验，鉴于径向基神经网络[7]和马尔科夫链[8]在滑坡变形预测中的适用性，利用两者构建滑坡变形的分项预测模型，且考虑到降雨是滑坡变形的主要诱因，且其具明显的季节性特征，使得季节性Kendall检验适用于滑坡变形趋势判断。综合上述内容，本文以滑坡变形监测成果为基础，先利用经验模态实现其变形信息分解，即将变形数据分解为主趋势项和误差项，且为保证分解结果的最优性，提出对传统经验模态进行优化处理；其次，再利用优化径向基神经网络实现主趋势项的变形预测，并利用马尔科夫链实现误差弱化预测，两者综合实现滑坡变形的组合预测；最后，再利用季节性Kendall检验进行滑坡变形的趋势判断，以佐证预测结果的准确性。

1 基本原理

本文分析思路主要包含3个步骤。

(1) 利用经验模态(Empirical Mode Decomposition，EMD)分解滑坡变形数据，且为保证分解过程的准确性，利用多种优化方法实现其参数优化，以得到最优分解结果。

(2) 在前述滑坡变形数据信息分解基础上，利用径向基神经网络(Radical Basis Function，RBF)和马尔科夫链实现滑坡变形的组合预测。

(3) 利用季节性Kendall检验实现滑坡变形趋势判断，以佐证预测结果的准确性。

结合上述分析步骤，将本文涉及方法的基本原理详述如下：

1.1 信息分解模型的构建

在滑坡变形监测过程中，受监测条件限制，滑坡变形数据含有一定的误差信息，即：

yt=rt+εt

(1)

式中：yt为变形值;rt为变形真实信息,即主趋势项;εt为变形误差信息,即误差项。

由于误差信息存在，会对后续分析结果造成一定影响，进而需对滑坡变形数据进行信息分解；同时，经验模态是一种常用的信息分解方法，已被广泛应用，其适用性不言而喻，但传统EMD无法完全消除白噪声，进而存在模态混叠现象，为保证滑坡变形数据信息分解的准确性，多种优化方法应运而生，如互补式集合经验模态分解(CE-EMD)[9]、集合经验模态分解(E-EMD)[10]和自适应局部均值经验模态分解(ALM-EMD)[11]，鉴于各种优化分解模型的适用性差异，提出对3类优化经验模态分解均进行试算，通过对比三者的分解能力来确定最优信息分解模型。

在滑坡变形数据信息分解过程中，以往多利用信噪比和平滑度指标进行分解效果评价，鉴于两者基本原理的差异性，提出利用两者归一化值构建变形数据信息分解的效果评价指标g：

g=g1+g2

(2)

式中：g1为信噪比的归一化值;g2为平滑度指标的归一化值。

据综合指标g即可判断信息分解结果的优劣，判据为：g值越大，说明分解效果相对较好；反之，说明分解效果相对较差。

1.2 变形预测模型的构建

如前所述，通过优化经验模态将滑坡变形数据分解为了主趋势项和误差项；在变形预测模型的构建过程中，应对主趋势项和误差项进行针对性的模型构建，其中，滑坡变形的真实信息属主趋势项，其规律性较为明显，而滑坡变形的误差信息属误差项，具有较强的随机性；考虑到RBF神经网络的非线性预测能力及马尔科夫链的误差弱化能力，将RBF神经网络作为滑坡变形的主趋势项预测模型，并将主趋势项的预测误差与经验模态分解的误差信息叠加形成残差项，并利用马尔科夫链实现其弱化处理，最后，两者预测结果叠加即为滑坡变形的最终组合预测结果。

(1) 主趋势项预测模型的构建。神经网络是一种常用的智能预测模型，已被广泛应用于岩土领域，其中，RBF神经网络具有较强的自学能力，适用于非线性预测，进而利用其实现滑坡主趋势项的变形预测。

在RBF神经网络的预测过程中，其通过三维空间映射来提高非线性预测能力，其预测过程为：

(3)

式中：yi为预测值;wij为连接权值;h为隐层节点数;σ为核函数宽度;xi为输入值;ci为核参数。

值得指出的是，RBF神经网络虽具有较强的非线性预测能力，但其基本原理存在一定不足，如隐层节点数和连接权值均随机设定，主观性较强，难以保证其客观准确性；因此，为保证主趋势项的预测精度，应对上述两参数进行优化处理，即：

①隐层节点数的优化处理。在传统神经网络的预测过程中，多采用经验公式确定隐层节点数，即：

(4)

式中：m,n为输入、输出层节点数。

经计算得到，隐层节点数的经验值为15，为保证隐层节点数的最优性，以其为中心，扩展隐层节点数的取值范围至9—21间的奇数值，并通过逐步试算对比来确定最优隐层节点数。

②连接权值的优化处理。由于连接权值具有范围取值特征，难以通过上述试算法实现其优化处理，考虑到人工鱼群算法(artificial fish swarm algorithm，AFSA)具有较强的优化能力，利用其实现RBF神经网络的连接权值优化，优化流程见图1。

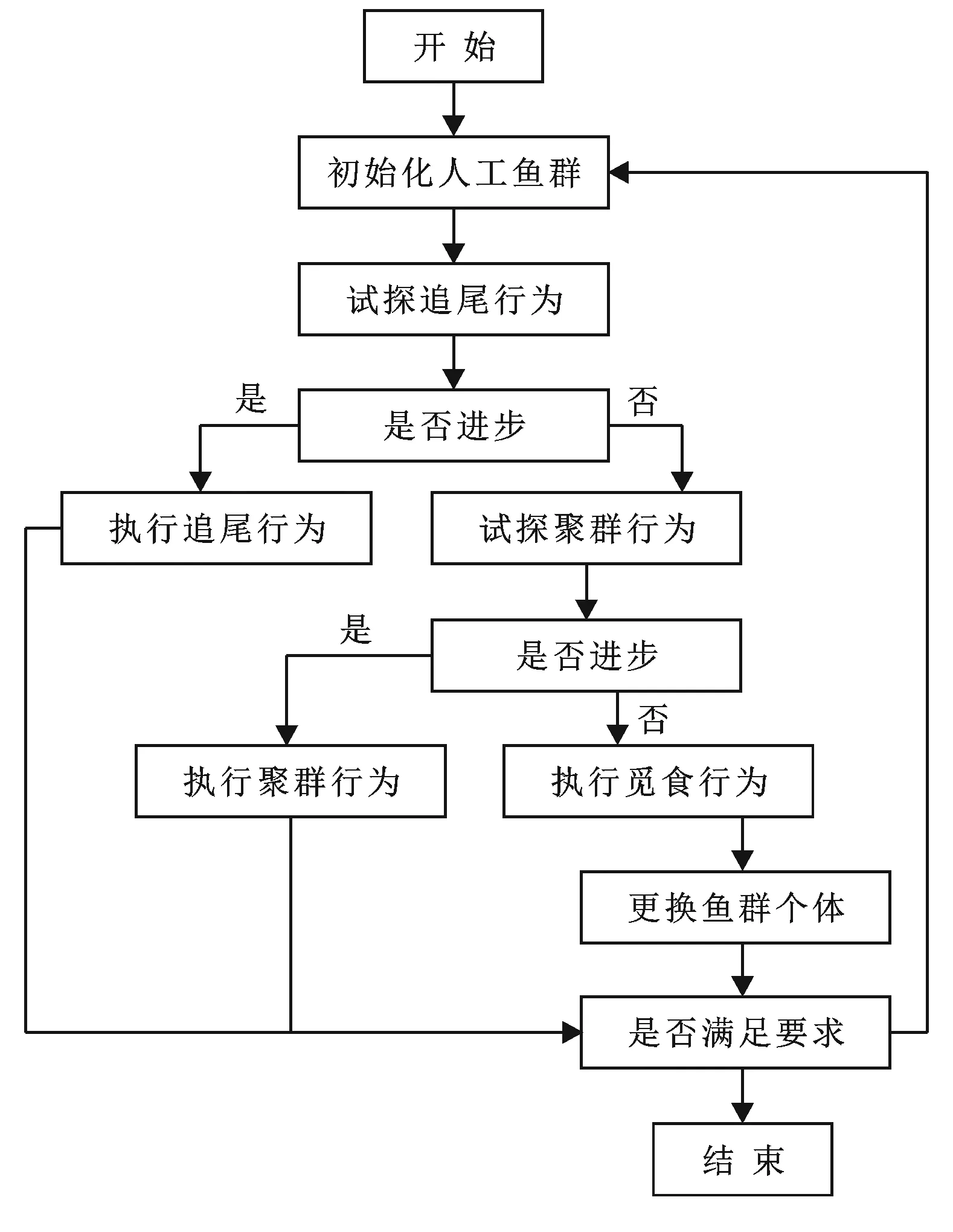
图1 AFSF算法的优化流程

通过上述两步骤的优化处理，有效保证了RBF神经网络模型参数的最优性。

(2) 残差项的预测模型构建。如前所述，将主趋势项的预测误差与经验模态分解的误差信息叠加形成残差项；由于马尔科夫链是一种典型的随机模型，进而利用其实现残差项的预测处理是可行的，其预测过程为：

①状态划分。以前述残差项为基础，据其误差范围，进行残差项的状态划分；并结合该文实例，共计划分为5个状态。

②计算状态转移概率。以某状态为基础，统计其转移至另一状态的次数，再统计其在总样本数中的出现次数，两者相除，即可求得该状态条件下的转移概率。

③构建构造矩阵。以前述转移概率为基础，构建概率矩阵，通过设置转移步数长度，即可得到相应状态条件下的预测结果，达到误差弱化预测的目的。

将前述主趋势项预测结果与残差项预测结果叠加即为滑坡变形的最终预测结果；同时，在预测效果评价过程中，确定相对误差为评价指标，其值越小，说明其预测效果越好；反之，预测效果越差。

1.3 预测结果可靠性验证模型的构建

受周期性降雨影响，滑坡变形具有季节性特征，且鉴于季节性Kendall检验是一种非参数检验方法，能很好反映滑坡变形数据中的季节变化规律，因此，利用其实现滑坡变形的趋势性判断，以佐证前述变形预测结果的可靠性。在季节性Kendall检验的分析过程中，先计算其初步统计量S：

(5)

式中：Xi,j为相应时间节点处的变形值; sgn(θ)为反应函数(当θ<0时,其值为-1;当θ>0时,其值为1;当θ=0时,其值为0)以初步统计量S为基础，将进一步计算最终评价指标τ：

(6)

式中：var(S)=〔n(n+1)(2n+5) 〕/18,n为分析样本数。

当τ>0时，得滑坡变形具上升趋势；反之，具下降趋势。同时，将τ值的绝对值与临界值τa进行对比，若前者较小，说明检验过程无效；反之，说明检验过程有效，能判断滑坡变形趋势，且鉴于临界值τa与检验水平a相关。因此，以检验水平a为基础，进行滑坡变形的趋势等级划分，具体标准见表1。

表1 滑坡变形趋势等级划分标准

2 实例分析

2.1 工程概况

王家坡滑坡位于陕西省西安市灞桥区王家坡村，区内具白鹿塬斜坡地貌，高程间于454～741 m，斜坡坡度间于15°～35°，地形起伏较大。据调查成果，该滑坡纵向长约300 m，宽约150 m，前、后缘高程差85 m，斜坡坡度15°，面积约3.70×104m2，厚度变化差异较大，平均厚度18 m，体积为9.06×105m3，属中型土质滑坡。

近年来，王家坡滑坡的变形加剧明显，严重威胁区内居民的生命财产安全，为实时掌握其变形动态，在其滑坡中部布设了两个监测点，即2#监测点和3#监测点，经统计，得到2018年10月17日至2019年8月13日共计300 d的变形数据[12]，由于原始监测成果具非等距特征，为便于后续分析，以原始监测成果为基础，利用matlab软件的cftool工具箱进行3次样条插值拟合，并将拟合结果按5 d/次的频率进行划分，共计得到60个周期的变形数据(见图2)。

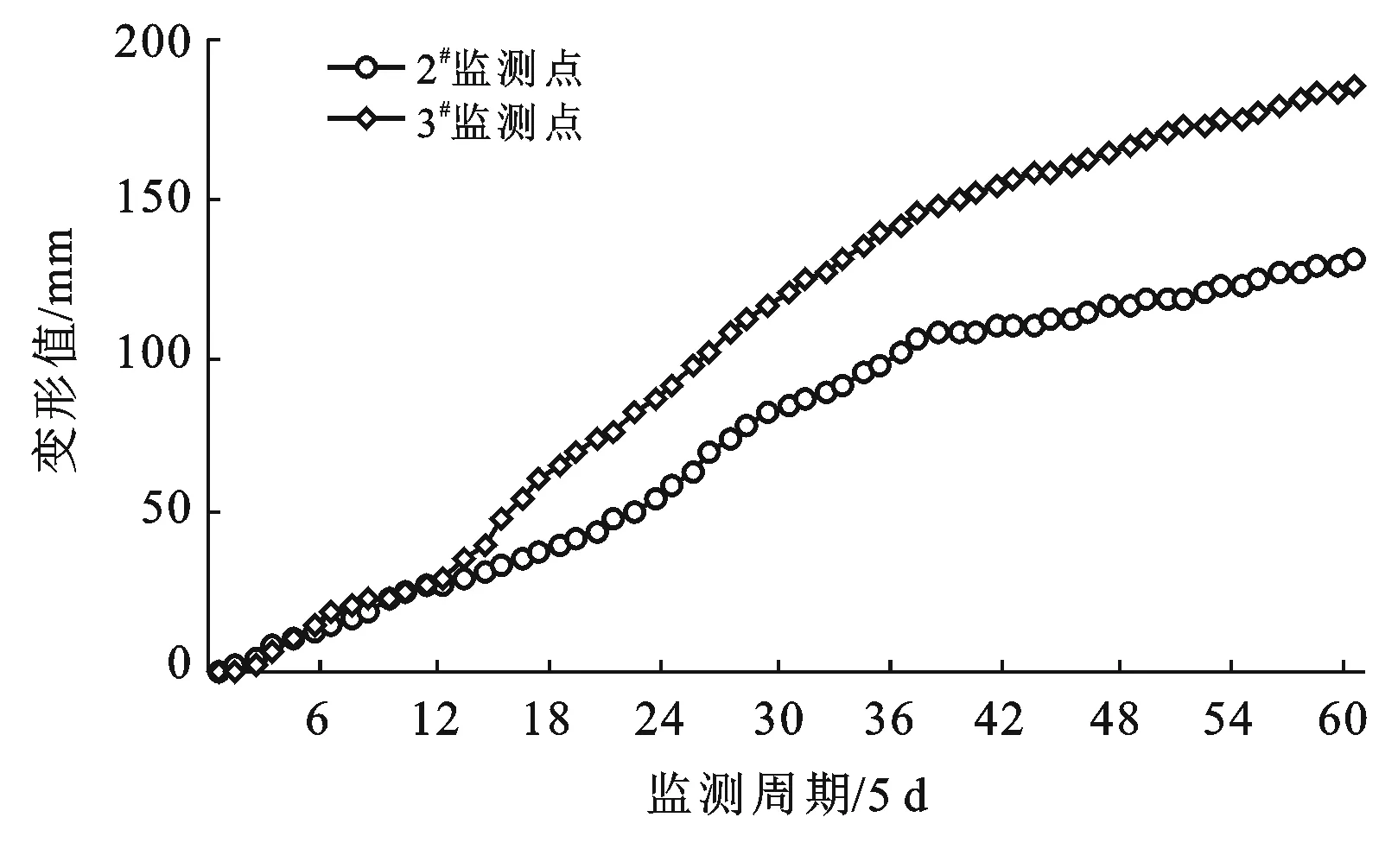
图2 滑坡变形监测成果

为充分验证该文变形预测思路的有效性，以2#和3#两监测点的变形监测成果为数据来源，开展验证分析研究。

2.2 信息分解结果与分析

对不同优化处理后的经验模态分析结果进行统计，结果见表2。如表2所示，不同EMD模型的分解效果存在明显差异，且3种优化模型较传统EMD模型的g值均有不同程度的提高，说明通过优化处理能有效提高滑坡变形信息的分解效果；对比3种优化EMD模型的分解效果可知，CE-EMD模型的分解效果相对最优，其次是ALM-EMD模型和E-EMD模型，进而确定该文滑坡变形数据的分解方法为互补式集合经验模态分解。

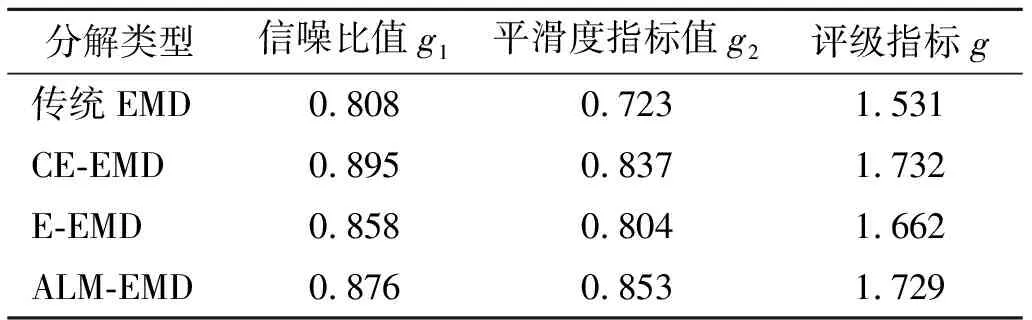
表2 不同优化处理后的经验模型EMD分解结果

2.3 变形预测效果分析

在变形预测过程中，将监测样本分解为两期，1—30周期为中期，31—60为后期，对两期样本均开展预测分析，不仅能验证该文预测思路的滚动预测能力，还能验证该文预测模型的稳定性，其中，中期的训练样本为1—25期样本(监测时间：20181017—20190219)，验证样本为26—30期样本(监测时间：20190219—20190316)，而后期训练样本为1—55期样本(监测时间：20181017—20190719)，验证样本为56—60期样本(监测时间：20190719—20190815)，外推预测4个周期(监测时间：20190815—20190904)；同时，为充分验证该文预测过程中不同优化方法的合理性，以2#监测点的中期预测为例，详述不同优化阶段的预测效果。

(1) 中期预测效果分析。

①主趋势项预测分析。按照RBF神经网络的优化流程，先对其隐层节点数进行优化筛选，结果见表3。据表3可知，不同隐层节点数对应的预测效果存在一定差异，验证了隐层节点数优化筛选的必要性，且随隐层节点数增加，平均相对误差值具先减小后增加趋势，即当隐层节点数为19时，具有最小的平均相对误差值，值为2.41%，进而确定RBF神经网络的隐层节点数为19。

表3 隐层节点数优化筛选结果

其次，再利用AFSA算法优化RBF神经网络的连接权值，预测结果见表4。

据表4可知，经AFSA算法的优化处理所得预测结果的最大、最小相对误差分别为2.63%和2.16%，平均相对误差为2.38%，相较于表3中的预测精度略有提高，验证了AFSA算法对连接权值优化的有效性。

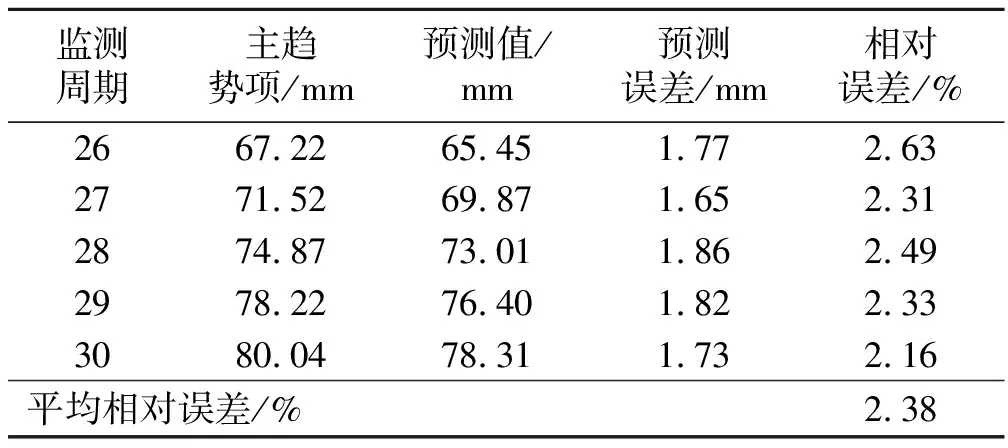
表4 连接权值优化预测结果

据前述分析，在主趋势项预测过程中，通过隐层节点数和连接权值的优化处理，能逐步提高预测精度。

②残差项预测分析。上述已实现了主趋势项预测，据预测结果，通过参数优化虽能一定程度上提高预测精度，但预测精度仍相对偏低，加之信息分解后剩余的误差信息，使得预测误差相对更大，按论文思路，再利用马尔科夫链进行残差项弱化预测，并将预测结果与前述主趋势项预测结果叠加，求得两监测点的中期预测结果见表5。

据表5可知，在2#监测点的预测结果中，平均相对误差为1.87%，相较于主趋势项预测结果，预测精度得到了明显提高，说明马尔科夫链能有效弱化残差项，且其最大、最小相对误差分别为2.04%和1.73%，具有较高的预测精度；同时，在3#监测点的预测结果中，最大、最小相对误差分别为2.09%和1.68%，平均相对误差为1.86%，预测效果与2#监测点的预测效果相当，也具有较高的预测精度。

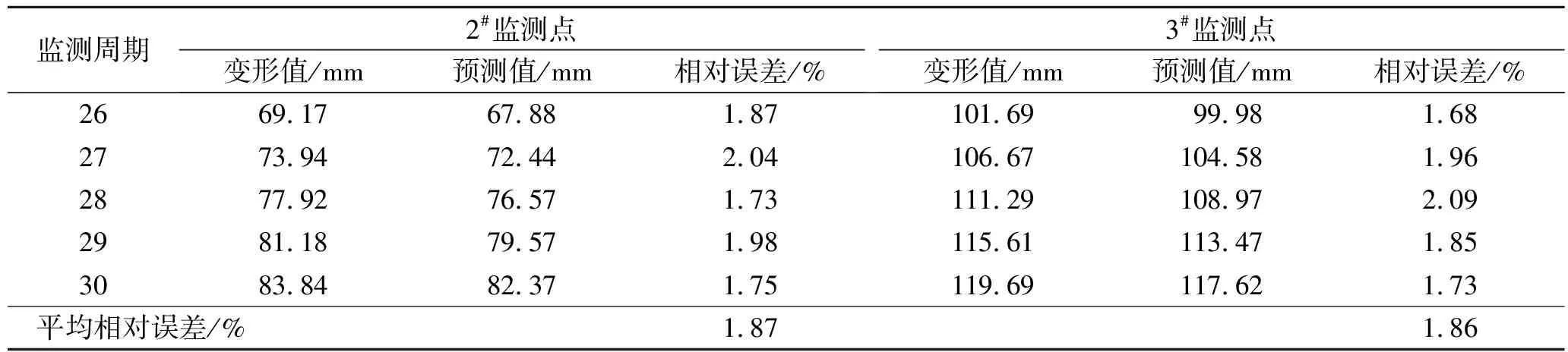
表5 滑坡变形中期预测结果

通过前述预测分析可知：在预测过程中，通过模型参数优化能有效提高主趋势项的预测精度，且马尔科夫链能有效弱化预测残差，达到进一步提高预测精度的目的；同时，通过两监测点的中期预测结果，得出该文预测模型具有较高预测精度，初步验证其有效性。

(2) 后期预测效果分析。再对滑坡后期数据进行预测分析，以校验该文预测模型的滚动预测能力，并进行外推预测分析，以掌握滑坡变形发展趋势。通过预测统计，滑坡后期预测结果见表6。据表6可知，在滑坡后期变形预测结果中，2#监测点的平均相对误差为1.93%，3#监测点的平均相对误差为1.81%，两者预测精度相当，且与中期预测效果一致，充分说明该文预测模型具有较强的滚动预测能力；同时，两监测点的外推预测结果显示，两者变形仍会进一步持续增加，并无收敛趋势，建议尽快开展滑坡灾害防治。通过上述滑坡变形预测分析，得出该文预测模型不仅具有较高的预测精度，还具有较强的滚动预测能力。

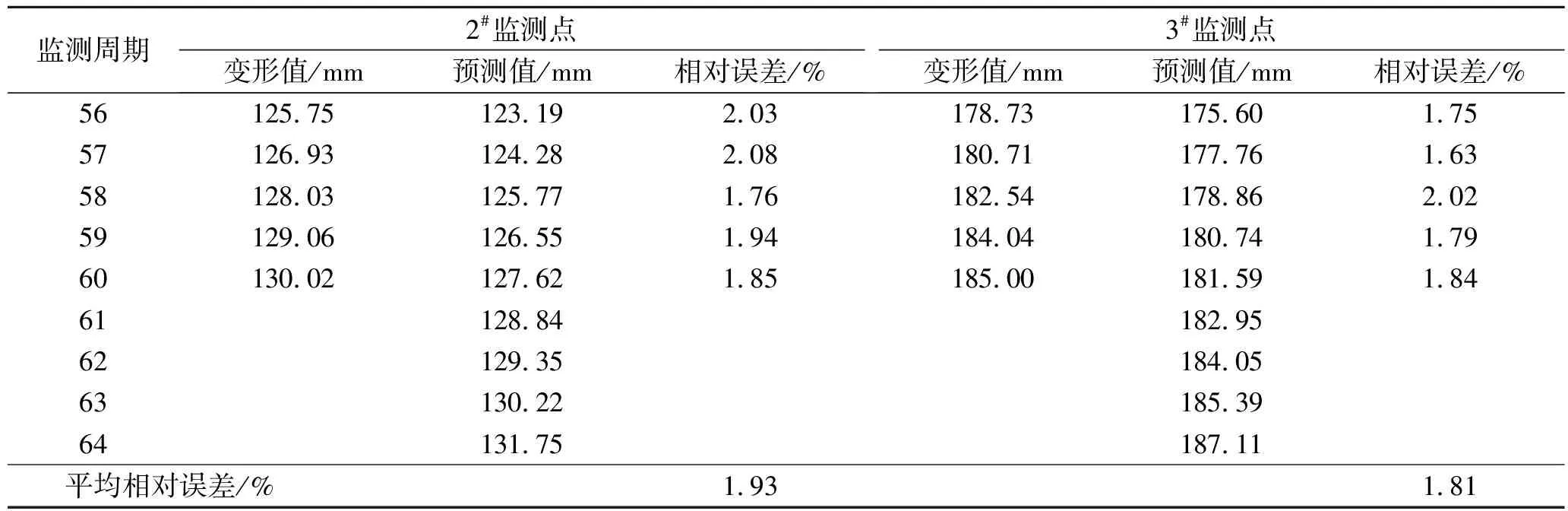
表6 滑坡变形后期预测结果

2.4 预测结果的可靠性验证

前述已完成滑坡变形预测分析，再利用季节性Kendall检验开展滑坡变形趋势判断，以验证前述外推预测结果的可靠性。

在季节性Kendall检验的分析过程中，将分析过程划分为整体趋势判断和分阶段趋势段，前者是以所有样本为基础进行分析，以实现滑坡变形的整体趋势判断，而后者是将滑坡变形样本等分为4个阶段，每个阶段20期样本，并对各阶段样本进行季节性Kendall检验，以掌握滑坡变形在不同阶段的趋势性。

(1) 整体趋势判断。通过分析统计，得到滑坡整体趋势判断结果(表7)。据表7可知，两监测点的τ值均大于0，说明两者均具上升趋势，且趋势等级相当，均为3级，与前述预测结果一致，验证了前述预测结果的可靠性。

表7 滑坡变形整体趋势判断结果

(2) 分阶段趋势判断。再对不同阶段的样本进行季节性Kendall检验，结果见表8。据表8可知，两监测点在不同阶段均呈上升趋势，但趋势性存在一定差异，总体表现为：随时间持续，趋势等级趋于增加。因此，进一步说明王家坡滑坡的变形趋势显著，其变形并无收敛趋势。

表8 滑坡变形分阶段趋势判断结果

3 讨论与结论

本文通过滑坡变形数据信息分解处理后的预测研究，主要得出如下结论。

(1) 受监测条件限制，滑坡变形数据含有一定的误差信息，其对预测分析具有显著影响，进而有必要开展滑坡变形信息的分解处理；同时，经验模型能很好实现滑坡变形信息分解，且通过优化处理能进一步提高分解效果，并以互补式集合经验模态的分解效果相对最优。

(2) 通过优化RBF神经网络对主趋势项的预测处理，得出模型参数优化能有效提高预测精度，且通过马尔科夫链的残差弱化处理，可达到进一步提高预测精度的目的，因此，得出该文预测模型具有较高的预测精度，能有效实现滑坡变形预测。

(3) 通过可靠性验证，得到变形趋势判断结果与预测结果也较为一致，充分说明该文预测模型具有较高的可靠性。

本文仅以陕西省内的滑坡实例进行验证分析，由于滑坡所处区域性条件的差异，建议在后续条件允许前提下，以进一步佐证其准确性。