基于图像修复的无监督表面缺陷检测方法
胡广华 王宁 何文亮 唐辉雄
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
纳米材料、手机屏幕、织物、铸件等产品表面上存在的形状各异的缺陷会严重影响产品的经济价值,甚至会造成安全隐患,因此缺陷检测是工业产品质量检测中至关重要的一环。虽然传统的缺陷检测方法能够有效检测织物、屏幕等背景均匀、图像特征显著的规则纹理表面的缺陷,但由于欠规则纹理表面缺陷具有各向异性、非线性、非均匀、易混淆等特征,传统的方法难以有效检测欠规则纹理表面的缺陷区域。
现有的表面缺陷检测方法可以分为3大类:基于统计学的方法、基于频域分析的方法和基于学习的方法[1]。基于统计学的方法有灰度共生矩阵[2]、直方图统计[3- 4]等。基于频域分析的方法主要包括傅里叶分析[5]、最优Gabor滤波器[6]和小波分析[7]等。基于统计学的方法和基于频域分析的方法需要缺陷和正常纹理图像之间具有较高的对比度,成像环境较为苛刻,在工业应用中适应性较差。而基于学习的方法适应性相对较强,只需要一定的训练数据和高性能运算单元即可建立检测模型。随着近年来机器学习、深度学习研究领域不断取得突破,基于学习的缺陷检测方法成为了缺陷检测的主流方法。基于学习的缺陷检测方法可以进一步分为有监督学习方法和无监督学习方法[8]。典型的有监督学习方法如单阶段检测网络YOLO[9]和SSD[10]、两阶段检测网络Faster- RCNN[11]等,需要大量的正常纹理样本和大量的缺陷样本来进行模型的训练。对这些样本数据的标注需要巨大的人力成本,同时由于人的主观性,会在标注结果中不可避免地引入人为偏差。另外,有监督学习方法无法学习到未包含在训练集中的“未知”缺陷信息,需要训练集尽可能地包含所有缺陷类型的数据。而无监督学习方法仅需少量正常样本即可完成网络模型的训练工作,吸引了许多研究人员参与到无监督学习的研究工作当中。根据处理空间的不同,可以将无监督学习分为基于图像空间[12]和基于特征空间[13]两种方法。前者在图像空间中,通过网络模型对缺陷进行重建,根据重建图像和待测图像之间的差异来进行缺陷检测;后者在特征空间中,通过正常纹理样本和缺陷纹理样本特征分布之间的差异来判断当前区域是否为缺陷区域。目前的无监督学习方法通常使用自编码器[14]和生成对抗网络[15]及其变种[16- 18]作为模型,多用于简单、统一的规则纹理表面缺陷检测,而对于非均匀性、非周期性的欠规则纹理表面,由于数据的发散性,训练后的网络模型容易生成和原图高度相似的重建图像,无法有效区分正常纹理和缺陷。
目前的图像修复方法主要根据图像中已知内容来恢复缺失区域内容。Pathak等[19]提出了一种上下文编码器,将深度学习应用到图像修复任务中。对于带有缺失区域的图像,通过自编码器生成重建图像,通过使损失函数中的中间损失和对抗损失最小化,可成功预测缺失区域的图像内容,但图像的失真度较高。Yeh等[20]提出了一种基于深度卷积生成对抗网络(DCGAN)的图像修复方法,使用预训练好的生成对抗网络(GAN)进行反向传播来推断图像内容。Wu等[21]提出的GP-GAN模型,利用梯度方法和GAN来进行合成图像的高分辨率融合任务。目前的图像修复技术主要用于图像编辑、虚拟现实、艺术作品修复等场景,使用大规模的数据集来训练网络模型理解图像的全局信息,对图像中的缺失区域进行补全和修复。
现有的对复杂、欠规则纹理的有监督学习方法需要大量标注后的缺陷样本,但由于这些缺陷样本难以囊括所有缺陷类型,故难以产生良好的检测效果。基于正常纹理样本学习的无监督学习方法通过训练使网络模型习得正常样本分布的重建和判别能力。当输入样本具有异常的纹理时,可能会生成不同于正常纹理的样本图像[8]。该学习任务的难点在于如何尽可能高精度地重建正常纹理区域,同时差异化地重建缺陷纹理区域,使得缺陷纹理区域和重建图像中的对应区域尽量不同。针对这些问题,本文提出了一种基于图像修复的无监督学习缺陷检测方法。该方法首先人为地在样本图像中设置缺失区域,利用网络模型来预测缺失区域的内容并对缺失区域进行填充;然后通过评估填充内容和真实内容的结构相似性(SSIM)评价图像和残差图像来判断当前区域为缺陷区域的概率;最后通过实验分析本文算法的性能。
1 基于图像修复的无监督检测模型
本文的检测算法分为训练阶段和测试阶段两个阶段。在训练阶段,人为地在仅包含正常纹理的样本图像中设置像素缺失区域,由生成对抗网络来预测缺失区域中的内容并进行修复和填充,通过训练迫使填充内容逼近真实图像中的内容,从而训练出理解正常纹理图像高层语义信息的网络模型,提高网络模型对于“未知”缺陷的泛化能力。在测试阶段,当缺失区域中带有缺陷图像时,网络模型填充到缺失区域的内容与真实图像中的内容存在显著的差异,本文使用基于残差图像和SSIM评价图像的方法来判断当前区域为缺陷的概率,然后使用阈值分割来完成缺陷检测和分割工作。
1.1 训练阶段
训练阶段的模型框架如图1(a)所示。首先,生成一幅与采样自原图像Isrc的输入样本x具有相同尺寸的掩膜图像M,其中缺失区域的长和宽分别为图像长和宽的一半。根据掩膜图像和输入样本图像获取遮掩后的样本图像x′,即

(1)
式中,i和j分别为像素所在图像位置的行编号和列编号。

判别器D的损失函数[18]可以表示为
(2)

生成器G的对抗性损失可以表示为
(3)
生成器G在生成过程中的重建损失Lrecon表示为掩膜遮盖区域重建损失和未遮盖区域重建损失的加权和:


图1 基于图像修复的无监督表面缺陷检测方法
Lrecon=αLunmasked+(1-α)Lmasked
(4)
式中,α为权重系数,Lmasked为掩膜遮盖区域的重建损失,Lunmasked为未遮盖区域的重建损失。
为提高重建精度,在传统的均方和误差(MSE)的基础上引入了SSIM误差[22- 23]:

(5)

(6)
式中,β为权重系数,I为与输入样本同样尺寸的单位矩阵,⊙表示按位相乘。SSIM的计算式可表示为
(7)
式中,μx、μy分别为待比较的图像块x、y的平均灰度值,σx、σy分别为x、y的灰度标准差,σxy为x和y之间的协方差,C1、C2是防止分母为0的常数。
为了提高重建的稳定性,进一步在生成器损失函数中引入隐变量损失Llat来约束模型训练中的隐变量。Llat定义为判别器D的中间计算结果zreal和zfake的均方和误差:
Llat=MSE(zreal,zfake)
(8)
式中,zreal和zfake分别为原始样本和重建样本图像输入到判别器中的中间层隐变量。
综合式(3)、式(4)和式(8),生成器G的损失函数表达式为
LG=Lrecon+λadvLadv+λlatLlat
(9)
式中,λadv和λlat分别为对抗性损失Ladv和隐变量损失Llat的权重系数。
1.2 测试阶段

(10)
式中:G()为生成器G的前向传播函数;M为由一系列0/1掩膜图像Mi组成的集合,可以表示为M={M1,M2,…,MN},N为集合中的掩膜个数,本文取N=4。实验发现,随着N值的增大,缺失区域在整幅样本图像中的面积占比减小,模型仅预测小范围内的图像内容。过大的N导致模型无论是对于缺陷样本还是正常样本,都生成和原图像高度相似的样本图像,失去了引入缺失区域的意义。
真实缺陷尺度跨度往往很大,图2给出了不同尺度的缺陷被掩膜重建的效果。考虑缺陷在待测样本中的不同面积占比,分别取无缺陷的正常纹理、缺陷占据部分区域、缺陷占据全部区域3类样本,输入到网络模型中进行重建。观察图2(a)中重建样本组和遮掩后样本组发现,模型能够有效预测缺失区域的内容,经过组合后的重建样本和正常纹理的待测样本高度一致。图2(b)为缺陷占据部分区域样本的重建结果,其中缺陷区域占据输入图像约四分之一的面积。随着掩膜滑动到缺陷区域,模型根据其学习到的正常纹理分布信息来预测缺失区域的内容,重建出符合其邻域信息的正常纹理图像。比较图2(b)中重建样本与待测样本,观察到在缺失区域两者的图像内容明显不同。对于图2(c)所示的缺陷占据全部区域样本的重建结果,尽管其邻域信息均来自于缺陷区域,但模型用正常纹理的分布信息来对缺失区域进行重建,生成的重建样本和待测样本仍然有较大的区分。为了进一步提高模型对于正常纹理的重建精度,本文采取了对经过生成器的重建样本集合取平均值的方法。这导致了图3(b)中的重建图像和原始图像视觉效果高度相似,因此本文提出了如下的缺陷分割方法,以有效地区分缺陷纹理和正常纹理。
本文综合SSIM评价图像和残差图像来进行缺陷的最终识别和定位。残差图像中各个像素点的灰度值是原始图像和重建图像对应像素点灰度值之差的绝对值,如图3(c)所示。SSIM评价图像是通过在原图像和重建图像中设置固定大小的滑动窗口[24],根据式(7)计算两图像中滑动窗口对应区域的SSIM值,以给定的步长在图像平面上移动滑动窗口,对重叠区域取平均值,得到的SSIM评价图像如图3(d)所示。



图2 不同类型图像块的重建

图3 后处理过程中的图像
分别对残差图像Iresidual和SSIM评价图像ISSIM进行后处理,获得最终的二值化检测结果图像Iresult:
(11)
(12)
Iresult(i,j)=Iresidual(i,j)&ISSIM(i,j)
(13)
式中,δ1和δ2为分割阈值,&表示逻辑与运算。
NanoTWICE[25]中典型缺陷的检测图像如图3(a)所示,其中,前4行的输入图像为包含缺陷的图像,最后一行的输入图像为不包含缺陷的图像。可以看出:对于包含缺陷的图像,本文网络模型能成功地检测出图像存在的异常;对于正常图像,本文网络模型并没有错误地判断出图中存在的缺陷。这表明,利用本文方法对欠规则的纹理进行缺陷检测,结果是有效的。
2 实验结果与分析
2.1 实验环境
本文实验环境为Windows 10操作系统,显卡为NVIDIA TITAN Xp,使用Tensorflow深度学习框架进行训练。网络模型具体参数如表1和表2所示,其中Conv表示卷积网络层,Deconv表示转置卷积网络层,BN表示批归一化,LN表示层归一化。选用Adam优化器来训练网络模型,设定的学习率为0.002,patch尺寸设置为32×32,batch size取64,迭代次数为200,通过如表3所示的对照实验来确定模型在训练过程中损失函数的各项权重系数,其中AUC表示受试者工作特征(ROC)曲线下方的面积。可以看出,本文模型对不同的超参数设置具有鲁棒性,最终选取权重系数α为0.25,β为0.05,λadv为0.1,λlat为100。

表1 生成器参数

表2 判别器参数

表3 损失函数权重系数的选择
为便于比较,本文选择了基于l2-AE的缺陷检测方法[23]、基于DCGAN的无监督缺陷检测方法[26]、SSIM-AE[23]等无监督检测算法进行对比实验。为进一步研究本文算法的有效性,将本文提出的图像修复方法同时应用于l2-AE、DCGAN模型进行测试对照,并分别在具有规则纹理的织物数据集MVTec AD Carpet[27]和具有欠规则复杂纹理的纳米材料数据集NanoTWICE上进行实验。
2.2 评价指标
为了定量地评估本文检测算法的有效性,引入准确率A、查准率P、查全率R、F1度量以及ROC曲线作为评价指标,其定义分别为
(14)
(15)
(16)
(17)
(18)
式中,NTP为缺陷位置像素被模型正确判定为缺陷位置像素的数目,NFP为正常纹理区域像素被模型错误地判定为缺陷位置像素的数目,NFN为缺陷位置像素被模型错误地判定为正常纹理区域的像素数目,NTN为正常纹理区域像素被正确地判定为正常纹理区域的像素数目。ROC曲线的纵轴RTP表示整个数据集中被正确分类为缺陷区域的像素数目的比例,横轴RFP表示整个数据集中被错误地分类为缺陷区域的像素数目的比例。
2.3 实验结果分析
为了定量分析本文算法各主要环节的作用,设置了如表4所示的消融实验,分别开展了训练过程中不使用掩膜遮掩样本图像、不使用MSE损失、不使用SSIM损失、不使用隐变量损失、去除模型中的残差模块、不使用残差图像评估机制、不使用SSIM图像评估机制等组别实验作为本文算法的对照实验。表4中的对比结果表明,在训练阶段使用掩膜遮掩样本图像对缺失区域进行修复重建的方法,能够显著提升异常图像的缺陷检测能力。引入MSE损失使得缺陷检测方法在查全率和查准率上分别提升了16.40%和8.56%,而引入SSIM使得缺陷检测方法在查全率和查准率上分别提升了7.82%和17.56%。与引入MSE损失和SSIM损失所带来的性能提升相比,使用隐变量损失的提升程度较少,在查全率和查准率上分别提升了5.36%和2.91%。在网络模型中引入残差模块,提高了网络模型的重建精度,查准率提升了11.32%。与仅使用残差图像作为评价机制的对照组相比,使用SSIM图像作为评价机制的组别表现出更为优异的检测性能。结合残差图像和SSIM图像的评价机制能够有效提升模型对微小缺陷的检测精度,能够更为精确地检测出待测图像中的缺陷区域。
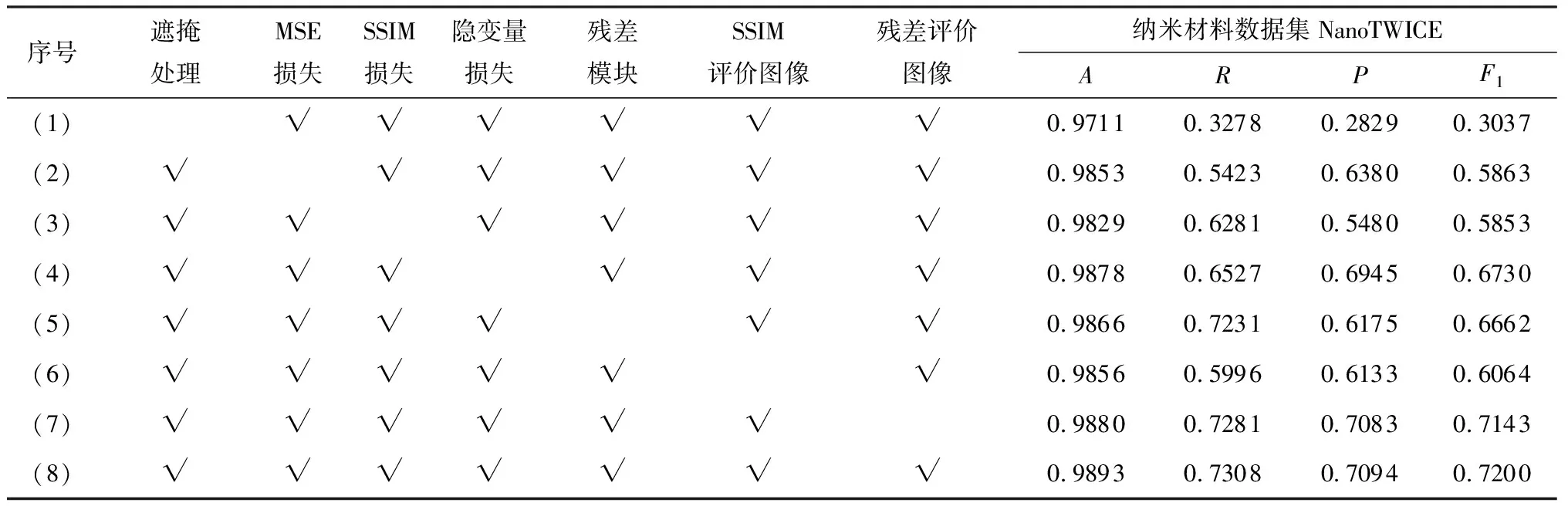
表4 消融实验结果
在规则纹理的MVTec AD数据集中,本文选取了Carpet样本作为实验对象,5幅正常图像作为训练集,89幅缺陷图像作为测试图像,图像分辨率均调整为256×256,实验检测结果如表5和图4所示,几种算法的ROC曲线如图5(a)所示。可以看出,对于规则纹理图像,各算法均能有效地检测出待测图像中的缺陷区域,但本文提出的算法能够更为精确地检测并分割出缺陷。
在欠规则复杂纹理的纳米材料数据集NanoTWICE中,本文使用了5幅正常纹理的图像作为训练集,40幅缺陷图像作为测试集,图像原始分辨率为1 024×672,典型的检测结果如表5和图6所示,几种算法的ROC曲线如图5(b)所示。基于l2-AE、DCGAN等生成模型的算法无法生成和原图像具有足够区分度的重建结果,难以通过残差图像阈值分割方法来获取缺陷的像素位置,分割出的结果多为正常纹理的高频信息,如图6(c)、6(e)所示。在训练阶段和测试阶段中增加了遮掩处理后,l2-AE、DCGAN的检测性能有了显著的提升,能够在一定程度上分割出缺陷区域,如图6(d)、6(f)所示。SSIM-AE能够有效地检测出图像中的缺陷区域,但仍然存在相当程度的错检和漏检。而本文提出的算法可以更精确地检测出原图像中的缺陷区域,表现出更为优异的性能。
从表5与图5可以看出:对于具有规则纹理的织物数据集MVTec AD,传统的基于重建的检测方法,如基于l2-AE、DCGAN的缺陷检测方法能够对缺陷区域进行有效检测。使用图像修复的方法后,基于l2-AE、DCGAN的缺陷检测方法的性能略有提升。对于复杂、欠规则纹理的纳米材料数据集NanoTWICE,l2-AE、DCGAN没有学习到其高层语义信息,生成和输入图像高度相似的重建图像,无法有效地检测纳米材料中的缺陷。在使用了图像修复的方法后,l2-AE、DCGAN对纳米材料中缺陷的检测性能均有了显著的提升。在NanoTWICE、MVTec AD Carpet数据集的检测实验中,SSIM-AE均表现良好,原因在于SSIM综合了亮度、对比度、结构3方面来对图像块间的相似性进行度量;本文算法的准确率、查全率、查准率、F1以及AUC等评价指标均取得了最高值,证明了所提出算法的优越性。

(b)GT图像

(c)l2-AE检测结果

(d)遮掩处理-l2-AE检测结果

(e)DCGAN检测结果

(f)遮掩处理-DCGAN检测结果

(g)SSIM-AE检测结果

(h)本文算法检测结果
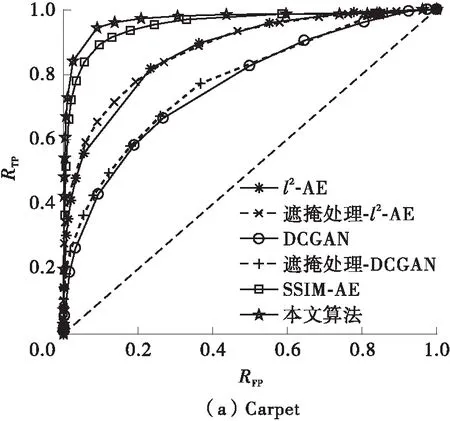

图5 不同算法的ROC曲线对比

(a)原图像

(b)GT图像

(c)l2-AE检测结果

(d)遮掩处理-l2-AE检测结果

(e)DCGAN检测结果

(g)SSIM-AE检测结果

(h)本文算法检测结果
为了评估本文算法检测不同尺度缺陷的性能,分别对不同尺度大小的纳米材料缺陷和织物缺陷进行了实验。待测图像大小为256×256,采样的patch尺寸为32×32,结果如图7所示。由于本文算法是通过取图像块中平均SSIM值的方式获取SSIM评价图,故对缺陷尺寸较大、与正常纹理差异较大、背景纹理规则的缺陷的检测精度较高,如图7(a)、图7(b)所示,但对缺陷尺寸过小、对比度过低的缺陷仍存在检测错误,如图7(c)、图7(d)所示。


图7 本文算法对不同尺度缺陷的检测结果
3 结论
本文提出了一种基于图像修复的无监督缺陷检测方法:在训练阶段,人为地在少量正常纹理样本图像中设置缺失区域,并利用生成对抗网络模型来预测缺失区域的图像内容,通过最小化损失函数来使得网络模型能够理解图像的高层语义信息;在测试阶段,将逐块遮掩后的待测图像输入至生成器中,生成对应的重建图像,计算待测图像和重建图像之间的残差图像以及SSIM评价图像,并对残差图像和SSIM评价图像分别进行阈值分割,最后通过联立两者的分割图像来完成缺陷的检测和分割工作。本文提出了结合重建损失、对抗性损失和隐变量损失的损失函数,并通过实验分析了各项损失对实验结果的影响。在具有规则纹理的织物数据集MVTec AD Carpet和具有欠规则纹理的纳米材料数据集NanoTWICE上的实验结果表明,本文算法与其他同类无监督检测算法相比,具有更优良的检测性能。

