基于数学形态学的故障行波测距方法

穆杉

（华北水利水电大学 河南省郑州市 450000）

近年来我国发展所取得的城市化成就越来越显著，在此过程中社会生产生活对电力的需求也越来越强。为了满足社会生产生活对电能的需求，针对电力系统的设计与运行保护工作受到了更高的关注，电力系统的覆盖范围在不断扩大，电力系统的功能也随之不断增强。如果电力系统的线路突发故障，社会工作和居民的正常生活都会受到波及，不利于当前我国的社会经济发展与建设。为了将电力系统突发故障所带来的不利影响与损失控制在最小范围内，加速修复故障问题的工作效率，应不断提升对电力系统运行故障检测的技术方法。总结过去电力系统故障的恢复经验，可以发现开展的故障位置筛查，占用率过多的故障恢复时间，故障修复效率大打折扣。而加装了故障测距装置后，可以提升故障发生位置筛查的实际效率，避免故障持续时间过长，给社会生产造成较大的损失。此外，加装了故障测距装置后，还可以实现对故障原因的细致分析，对提升电力系统安全性提供了极大地帮助。收集电路故障中的行波，能够发现其中包含的多种信息，如果能够充分利用这些信息，可以实现对电力系统运行过程的灵活保护。

1 行波测距概述

如果输电线路中的一段发生金属性短路，短路处会有附加电压源的出现。在附加电压源影响下，故障位置的两侧母线会有行波出现，所谓的“故障电压与电流”，其实就是正反向行波的累积，所以行波一般也有电压行波或电流行波的称呼。电桥测距原理图如图1 所示。

2 直流输电线路安全性保障工作存在的问题

2.1 运行检测管理制度不完善

我国的电力企业在发展的过程中，输电线路运检管理工作中存在的问题，出现的最重要的原因，是由于制度处于不完善的状态。制度的规范性和统一性，对于工作的正常开展具有重要的意义。现阶段电力企业继续应用传统的输电线路运行检测管理制度，在降低企业整体的生产经营质量的同时，会造成运检管理工作中岗位职责的混乱，导致在实际的运检管理工作中出现员工积极性不高、员工的专业技术水平以及综合素质不高的问题。

2.2 运行检测技术相对落后

我国的电力企业生产管理工作，对比发达国家来说起步的时间较晚，在技术条件上有所欠缺，导致运行监测工作的质量和效率相对较差。另外，一些电力企业在发展的过程中，对于先进运检管理技术的认识不足，依然采用传统的、效率较低的运检管理模式。同时在对运检管理工作人员的培训以及先进技术人才的储备工作不足，也会导致输电线路运行检测管理工作中，出现各种实际问题。

2.3 运行检测工作效率较低

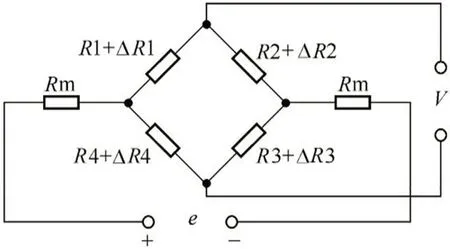
图1：电桥测距原理图

传统的输电线路运检管理工作中，采用的是区别管理的管理模式。将电力系统中，输电线路的运行工作与检修工作区分为两大方面的工作内容。这种区别化管理的管理工作方法，虽然可以保障运检工作的安全、顺利进行，但是，在一定程度上会降低输电线路运检工作的效率。输电线路运行检测工作的效率降低，会让运检的工作程序增多，对于输电线路运行过程中出现的问题，就无法进行及时的解决和改进。另一方面，运检工作中的工作程序过多，会导致程序处理系统的工作产生延迟，无法在发生紧急的运行问题时，作出合理的应急反应。

3 直流输电线路故障检测分析

3.1 完善运检管理制度

电力企业需要对运检管理模式的研究提升重视的程度，继续应用传统的运检管理模式并不现实，会在一定程度上提升企业经营管理过程中的风险，比不利于企业系统的正常运转。电力企业可以针对输电线路的管理工作制定出具体的规范文件，对输电线路运行检测中各个部门具体的工作职责进行明确的规定。

3.2 落实现场的移动化作业

现代化的输电线路精益化运检管理工作，可以通过现场移动作业的方式，应用智能化管理技术，提升运检管理工作的效率。在输电线路实际运行的过程中，进行现场移动化作业，需要依靠计算机技术与网络，将输电线路运行中的信息数据进行系统化的分析处理，将包括输电杆塔的高度、位置、技术参数等各类基础数据，上传到基础数据库中，方便管理人员对新加入的信息以及过往的信息进行查询和分析。

4 故障行波测距中的数学形态学方法

数学形态学的最初被研究出来的阶段，被应用于计算机数字图像处理工作中。特别是在计算机文字识别、医学图像分析的工作中，使用数学形态学方法取得了比较突出的应用效果。近年来，数学形态学方法凭借其独有的优势开始在电力系统保护中发挥作用。由于在电力系统领域中，数学形态学应用时长较短，所以在形态学结构元素选择、奇异点确定、滤波计算等方面还存在着一定程度的不足。但经过多年以来国内外研究人员的不懈努力，使其应用效果得到了提升。当前阶段，数学形态学在电力系统保护中的价值被越来越多人所肯定。

4.1 数学形态学滤波效果

在数学形态学方法下得到的滤波结果，与实际工作中的各项条件直接相关。这里所指的的条件具体包含干扰类型、频率、数据序列的采样率等。因此，在实际数学形态学方法开展的过程中，应对工作实际条件事先进行明确，重点分析实际的结合信号、干扰的特征。对电网的正常运行工作状态会产生的仿真电力信号检测，发现出现次数最高的干扰有高频连续干扰、随机背景噪声干扰等，会叠加到正弦信号中。若正弦信号幅值为1V、工频采样率为100kHz 的条件，为了合理评价数学形态学的滤波能力，就要在其工作过程中带入系数。将初始信号的系数记为0，可以发现随着系数的不断增高，噪声信号、被形态学进行滤波处理后的信号，这两种信号同初始信号间的差异就越为显著。对不同长度的混合滤波器和交替混合滤波器进行比较，发现在不同形态下滤波效果的直流偏差有着明显的图像变化特征。

4.2 AC行波辨识以及距离测算

使用数学形态学方法，辨别并分析电路系统故障发出的信号，这样能够快速准确地找到故障点位置。对电力系统故障的选线与选相研究中，同归对单相短路、两相短路、三相短路三种存在故障的线路，与处于正常工作状态的线路的不同电流波形图、形态学进行对比，可以研究发现以下几点特征。

（1）行波达到两侧母线。这一情况就表示电力系统在线路区间处有了故障问题。正常情况下初始行波具有高度的相关性，而通过明确这个原理就可以比较行波保护。

（2）如果将出现了故障的线路的电流行波分量，同正常运行的线路电流行波分量进行对比，会发现故障线路的电流行波分量更高，这是因为处于正常工作状态的线路信号分量，是在故障线路透射的作用下生成的。也就是说处于正常工作状态的线路信号分量，是故障的线路的信号分量中的一小部分。借由这一现象能够开展高质量的故障选线工作。

（3）故障行波信号的分量效果突出，没有发生故障的相行波分量不大，是因为没有发生故障的相电压电流信号分量是由电磁耦合引起的，借由这一现象能够开展故障选相工作。

（4）初始行波抵达母线的信号分量也是故障位置确切距离的重要体现，借由这一现象能够开展行波距离保护、故障距离检测工作。

通过对上述四点特征内容的分析，可以明确的是借助数学形态学来分析初始行波的效果是较为显著的。对电力系统故障的行波故障测距研究中，主要用到的研究方法是电流的线模分量，根据母线位置检测到的电流波形和形态学多梯度处理分析后的结果，可以计算得出初始行波和故障位置行波抵达时刻的时间差，带入公式后就可以大致估算出故障点的位置。

数学形态学在电力系统运行故障的检测中，发挥了快速、简洁的功能优势，作为滤波算法中的一种，数学形态学方法同样也是奇异点检测方法中的一种。如果在具体的工作过程中充分发挥出数学形态法的优势，就需要在目前乃至未来阶段不断加深对相关方法的研究力度和投入，保障数学形态方法的有效性，在暂态信号的监测工作内容中充分发挥数学形态学的功能。从上文对数学形态学在电力系统运行故障检测中的应用分析，可以明确的是这种方法可以有效地去除干扰信号对电力系统信号的不利影响。同时，这一方法可以起到比较显著的降噪效果。形态学方法具有更显著的优势，能够实现对不同信号、不同频率下电力系统的工作状态进行测定，能够改进既往应用的电力系统故障检测方法存在的不足之处。因此，在未来的电力系统运行故障检测工作中，应进一步强化对数学形态学的相关研究，使电力系统实际运行质量和效率得到提升。

5 结语

综合以上的分析内容，可知在对电网系统的运行故障进行检测的工作中，运用数学形态学的方法，能够起到较为突出的应用效果。特别是在技术应用的原理与计算量层面，数学形态学方法具有更显著的优势。能够实现对不同信号、不同频率下电力系统的工作状态进行测定，能够改进既往应用的电力系统故障检测方法存在的不足之处。因此，在未来的电力系统运行故障检测工作中，应进一步强化对数学形态学的相关研究，使电力系统实际运行质量和效率得到提升。