中性点不接地系统单相接地故障的分析与对策

林延生

（青岛西海岸公用事业集团易通热电有限公司 山东省青岛市 266400）

在中性点高电阻接地系统中，小电流可以最大限度地减小电弧对电器的危害，降低人身安全。此外，通过消除单相接地故障引起的瞬时电压跌落，降低变换器和电机驱动器产生的零序谐波电流，电能质量得到改善。中性点不接地系统具有同样的优点，但也存在暂态过电压问题。在这种情况下长时间运行，容易形成两相接地短路，间歇性电弧接地故障会导致整个电力系统产生过电压。此外，电力供应被破坏。

1 中性点不接地系统单相接地故障概述

运行经验表明，配电系统中的单相接地（SPG）故障占各类接地故障的大多数。中性点不接地系统在中低压配电网中得到广泛应用，由于其在发生 SPG 故障时故障电流小，线电压对称，负荷可连续运行1-2h。然而，由于故障相对接地电压为0（金属接地），相对接地电压的声音增加到如果在短时间内不选择，可能导致相间故障，造成更严重的三相短路故障。因此，准确识别故障线路对配电系统的安全稳定运行具有重要意义。在现有的配电网故障选线研究中，由于难以直接从时域分析配电网故障，基于各种等效变换（如小波变换、s 变换、希尔伯特-黄变换等）的研究成为热点。近年来，由于人工智能技术的发展，许多智能算法也被用于配电网 SPG 故障选线。然而，这些选线方法只注重信号处理，缺乏对系统故障本质的特征分析，算法复杂，实际工程应用较少。

2 中性点不接地系统单相接地故障研究现状

在过去的十年中，人们提出了一些原则和方法来解决这个问题。如果供电当局必须迅速查明故障并恢复供电，这种技术是必不可少的。各种接地故障选线装置广泛应用于配电系统中，对保护电网安全运行具有一定的积极作用。但现有的方法存在以下缺陷：

（1）文献[1]中基于零序电流基波的方法，受到CT 特性、线路长度、系统运行方式和过渡电阻值不一致的影响。

（2）文献[2]中基于零序电流的方法，当故障点远离互感器且线路短时，相位的确定不可靠。而不平衡电流、过渡电阻值、继电器工作电压死区和系统运行方式等都会影响故障线路的识别。

（3）对于文献[3]中基于谐波暂态分量的故障检测方法，采用小波分析工具对故障线路进行分析和检测，但对暂态信号的特征和利用方式缺乏进一步的研究，文献[4]中采用综合判据对故障线路进行检测，计算量大，难以实现判据的转换。

本文在暂态和稳态过程建模的基础上，建立了故障电流欠阻尼和过阻尼的数学模型。推导了SPG 后故障线路与声波线路相电流畸变的差异，提出了一种基于相电流畸变的故障选线方法。最后通过数值仿真对故障模型和选线原理进行了验证。

3 SPG故障条件下故障电流的数学模型

3.1 Karrenbauer变换

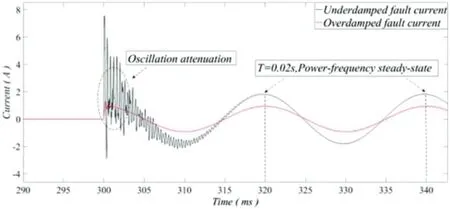
图1：系统欠阻尼和过阻尼故障时的故障电流

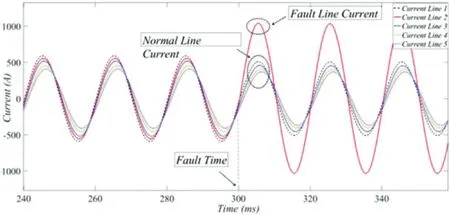
图2：10Ω SPG 接地故障时各线路的故障相电流

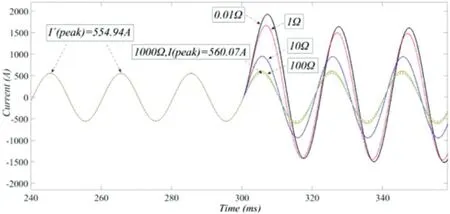
图3：不同接地电阻故障线路的故障相电流

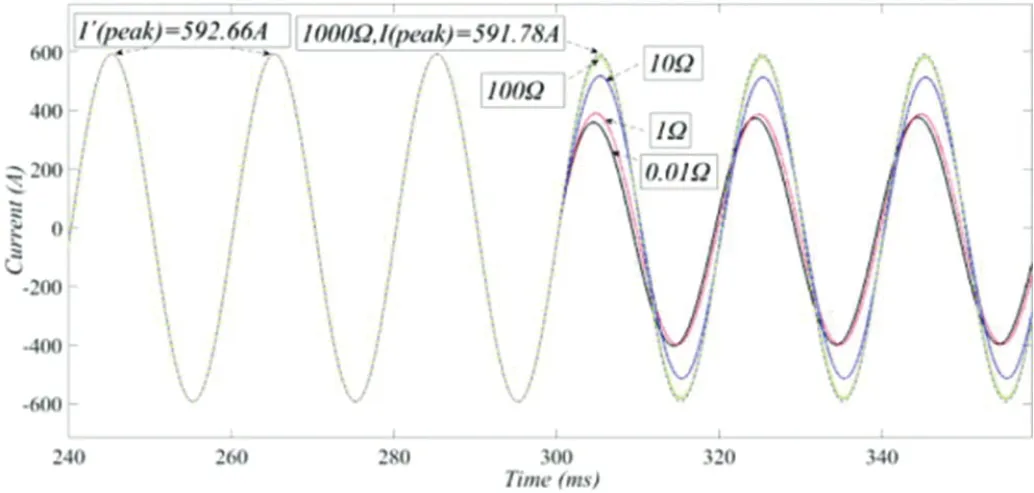
图4：具有不同接地电阻的声线(1 号线)的故障相电流

在电力系统暂态分析中，为了将耦合的三相系统解耦为三个独立的模网络，引入了Karrenbauer 相位模式变换：

上述坐标变换不涉及复数，更便于求解电磁暂态问题。因此，三相耦合系统的分析可等效为三个独立模块网络分析的线性叠加。

3.2 基于 Karrenbauer 变换和边界条件的复合序列网络

假设三相系统电压和线路参数是对称的，且线路间的分布电容被忽略。该系统共有 n 条架空线路，其中Zeqn为第 n 条线路的等效阻抗，其值由线路长度 l、变压器和负载决定：

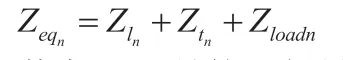
其中，Zln是第 n 根导线的等效集中阻抗，Ztn和Zloadn分别是第 n 根导线到高压侧的变压器漏阻抗和负载阻抗。当 SPG 故障发生在2 号线的 f 点时，边界条件为：

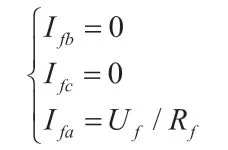
其中，Rf是接地点过渡电阻。通过上式和 Karrenbauer 相位-模变换可以得出：

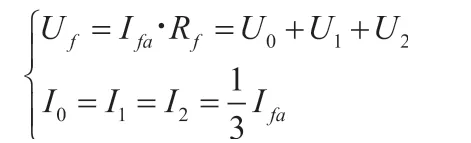
3.3 故障电流的数学模型

为了方便模型推导，等效复合网络模型可以简化为二阶等效电路 。其精度可以满足各种工程计算和仿真验证。建立模型的二阶微分方程为：

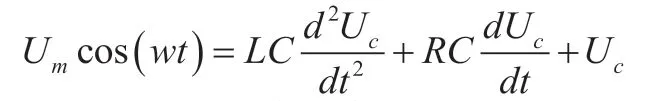
结合系统故障的初始条件（发生故障时，电容器C 两端的电压设置为U0）：

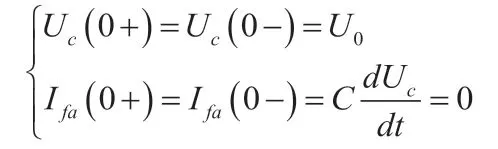
4 基于相电流畸变的SPG故障选线方法

4.1 基于相电流畸变的稳态故障特征

上述故障电流的数学模型表明，当系统进入稳态（指数部分的Ifa衰减为0）时，无论是过阻尼还是欠阻尼，当系统进入稳态（指数部分的Ifa衰减为0）时，Ifa都是一个正弦量，即：

4.2 基于相电流畸变的稳态选线方法

根据上一节描述的稳态故障特征，可以通过比较故障线路的故障相电流畸变率的正负值来选择故障线路:选择正相电流畸变线路作为故障线路。如果所有线路的相电流失真率相同，则母线故障。相电流畸变率是由线路本身在故障前后的电流有效值推导出来的，不受其他线路和故障暂态因素(故障初始相角、衰减因子等)的影响。过渡电阻 a 越小，故障线路与声线相电流畸变率的差值越大，选线效果越好。但应注意的是，为了减小误差，应在接地暂态过程完成后进行采集和计算。

4.3 仿真验证

在 Simulink 设立中低压典型配电系统。采用分布参数模型的5条倒置架空线长度分别为3、6、9、15、20km。

在 t = 3s 时，系统在欠阻尼和过阻尼故障条件下的故障电流如图1 所示。结果表明，对应于提到的故障电流，无论系统在故障后是欠阻尼还是过阻尼，在暂态过程中都会发生衰减振荡，直到过渡过程结束时才进入工频稳态。

当系统的 f 点是 SPG 通过10Ω 电阻时，每条线路的故障相(a)的电流如图2 所示。

根据模型参数可以计算出故障暂态过程(3-5τ)大约为0.9-1.5 ms，即系统在1.5 ms 故障后进入稳态。此时，可以提取各线路的故障相电流有效值(RMS) ，以验证上述稳态故障特征。仿真结果表明:只有故障前故障线路的故障相电流幅值增大，失真率为正，故障后故障线路的故障相电流幅值减小，失真率为负。

对故障选线方法进行仿真验证实验得出对于不同的接地电阻，每条故障线路的故障相电流和幅值线路（以1 号线为例）分别显示在图3 和图4 中。

仿真结果表明:接地电阻 Rf 越小， 故障线路电流对于不同的接地位置，该方法可以正确选择故障线路。接地位置越接近母线，图1 所示的简化故障模型越真实，故障线路的故障相电流失真率越大，该方法的效果越好。差值越大，故障线路和声线的故障相电流畸变率的差值越大，选线方法越好。对于高电阻接地，选线方法也可以正确选线。由于选线方法是基于系统的稳态故障特征，只要变压器采集量为稳态量，暂态因素(故障初始相角、暂态高频、衰减因子等)对选线方法没有影响。针对不同的线长和线数，进行了大量的仿真实验。仿真结果与理论一致，选线结果正确。

5 结束语

本文提出的故障选线方法只需采集稳态相电流进行选线，比传统的选线方法简单，大量的仿真结果表明，该方法的正确选线结果不受过渡电阻、接地点位置、暂态因素、线路长度和数量等因素的影响。