一种改进的基于最大复相关熵准则的自适应滤波算法

邱晨 向诗雨

（西南大学 重庆市 400715）

早期的滤波算法是基于均方误差准则的，如最小均方（least mean square, LMS）算法[1]和递归最小二乘（recursive least squares, RLS）算法[2]。基于均方误差的滤波算法虽然在高斯噪声环境下是比较理想的，但在非高斯噪声环境下其性能会大大下降。为了适应非高斯噪声环境，最大复相关熵准则（maximum complex correntropy criterion, MCCC）算法[3]作为一种局部相似性度量，近年来在复数域自适应滤波中得到了广泛的应用。与经典的基于均方误差的滤波算法相比，MCCC 不仅考虑了复数域，而且在非高斯噪声环境下，特别是在脉冲噪声的情况下，具有较好的鲁棒性和收敛性。

然而，传统MCCC 算法是基于最速下降理论的，不能较好地解决收敛速度和稳态值之间的矛盾。针对这个矛盾，本文基于不动点理论提出了一种改进的最大复相关熵准则（fixed-point maximum complex correntropy criterion, FPMCCC）算法，相较于MCCC 算法，所提出的FPMCCC 算法不再受限于自由参数，如算法中的步长，并且FPMCCC算法具有更快的收敛速度更快以及更小的稳态误差。

1 MCCC自适应滤波算法

1.1 复相关熵

与相关函数类似，相关熵是一种相似度量概念，可以有效地抑制脉冲噪声。复相关熵将相关熵的定义域从实数域扩展到复数域，对于给定的两个复随机变量C1=X1+jY1和C2=X2+jY2，C1和C2的复相关熵统计量[3]定义为：X1，Y1，X2和Y2都是实变量，代表取均值操作，为高斯核函数。

对于复数域的高斯核，核函数定义为：

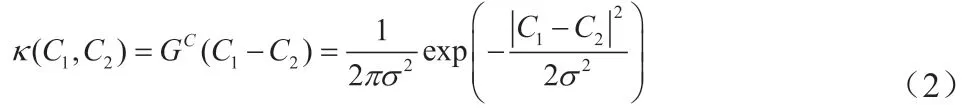
其中，σ 为核宽。

1.2 MCCC自适应滤波算法的原理

定义算法使用的系统模型为：

与此同时，MCCC 算法的代价函数由下式给出：

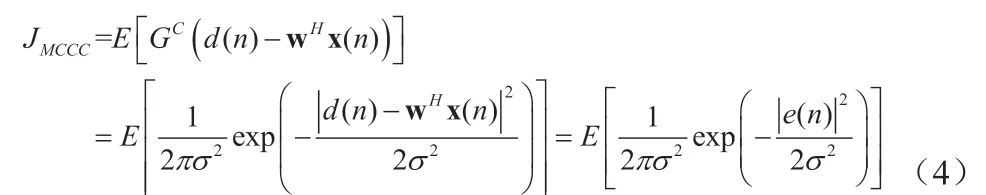
基于最速下降理论，由（4）可推导出MCCC 算法的权重向量的更新方程为：

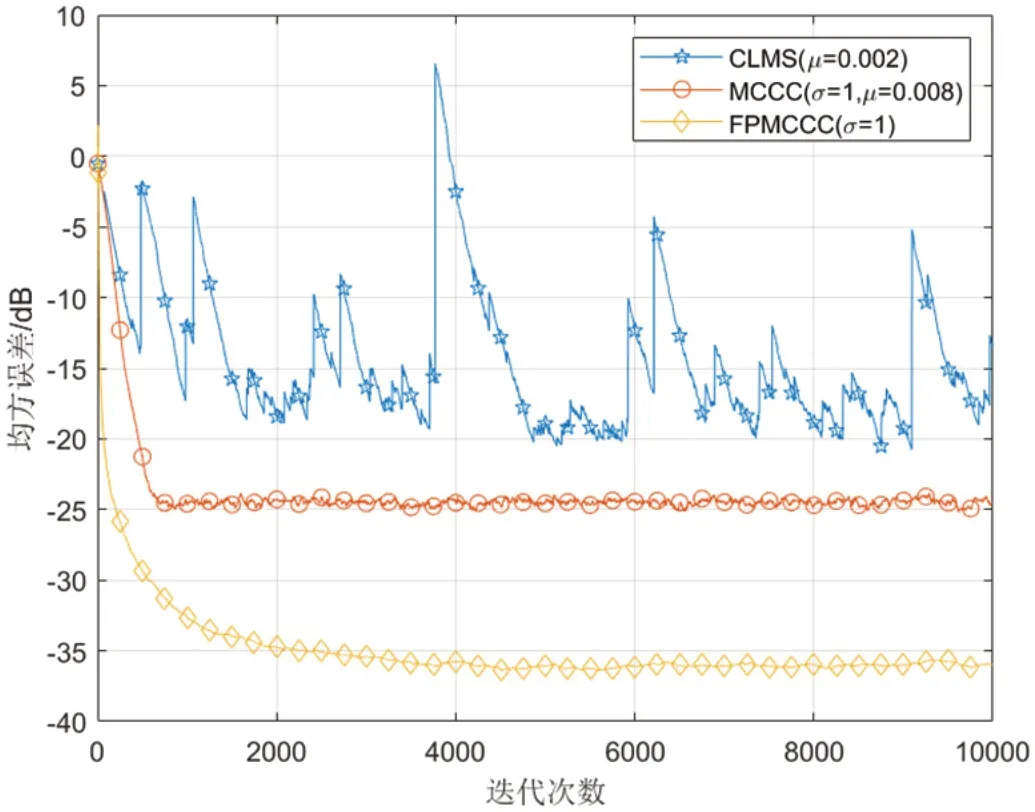
图1：算法之间的性能比较

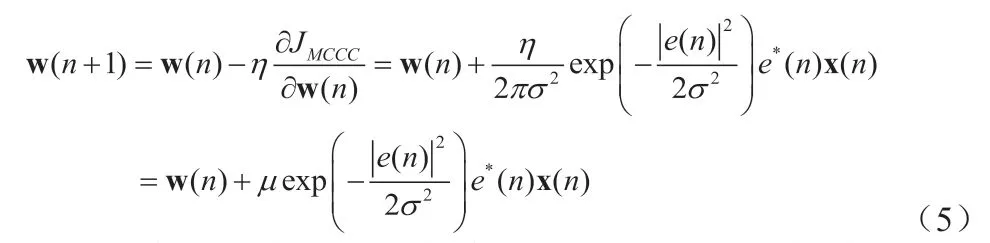
μ 为算法中的步长。当核宽σ →∞时，MCCC 算法退化至CLMS 算法。

2 改进的MCCC自适应滤波算法

由于传统MCCC 算法是基于最速下降理论的，其不能较好地解决收敛速度和稳态值之间的矛盾。针对这个矛盾，本文基于不动点理论对MCCC 算法进行来改进，提出的FPMCCC 算法能较好地解决收敛速度和稳态值之间的矛盾。

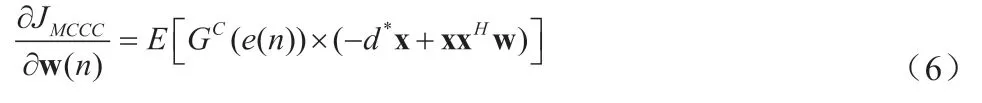
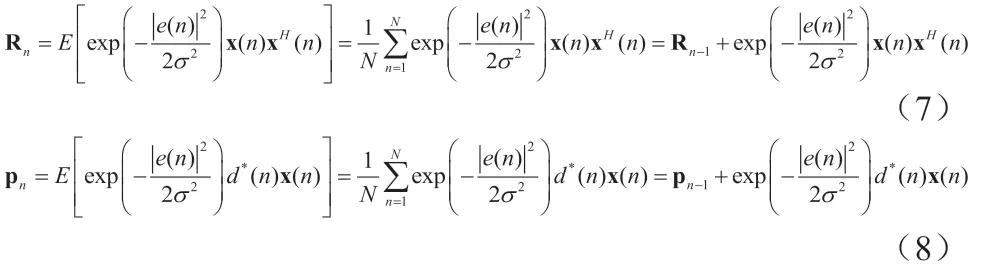
通过使用矩阵求逆定理[4]，（7）可以写为：

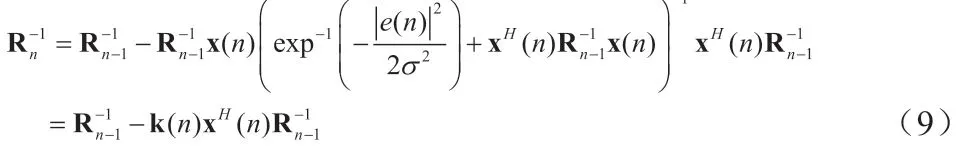
图2：风力信号大小

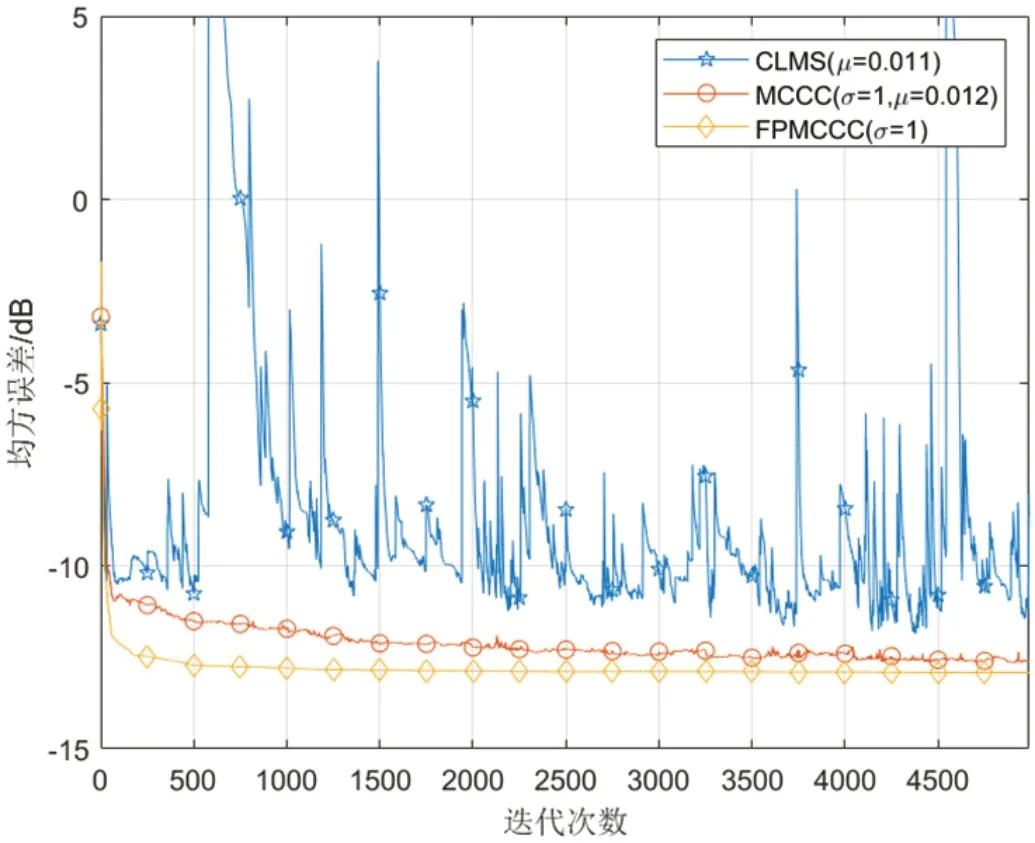
图3：算法之间的性能比较

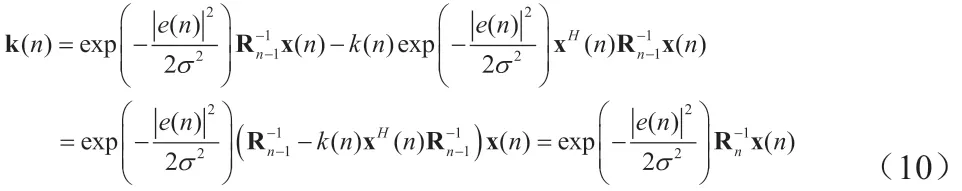
最后，FPMCCC 算法的权重向量的更新方程为：

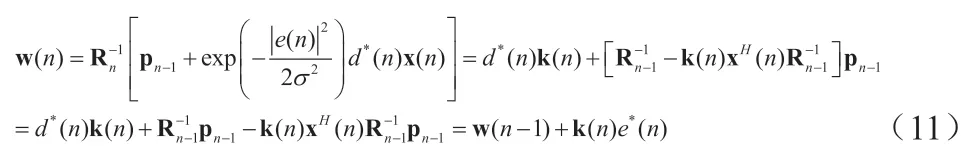
3 仿真结果分析

在实际应用中，噪声往往是非高斯的，为了体现FPMCCC 对非高斯噪声的优越性能，在仿真实验中均采用服从标准对称α 稳定(symmetric α-stable, SαS)分布的脉冲噪声，α 取值为1.5。在非高斯噪声情况下，本文进行了系统辨识和风力预测仿真实验，对比了FPMCCC、MCCC 以及文献[5]中的CLMS 之间的性能优劣。假定自适应滤波器的阶数m=5，随机生成权重其中代表的实部和虚部，N(μ,σ2)代表着具有均值μ 和方差σ 的正态分布。各实验分别进行100 次独立的仿真实验。

3.1 系统辨识

3.2 风力预测

为了进一步体现算法的现实应用性，将提出的FPMCCC 算法应用于一步风力预测。风力数据来自文献[6]，利用包含南北和东西向风速读数的数据，生成如下复数形式的风力信号（图2）：

为了证明FPMCCC 算法的鲁棒性，风力序列被脉冲噪声污染，同时利用依据均方误差通过图3 可以得出FPMCCC 算法仍具有最快的收敛速度及最低的稳态误差。

4 结语

鉴于传统基于最速下降理论滤波算法无法解决收敛速度和稳态值之间的矛盾，本文基于不动点理论提出了改进的基于最大复相关熵准则得自适应滤波算法。通过理论推导和仿真验证，将FPMCCC算法与现有算法的性能进行了比较，与现有算法相比，本文提出的FPMCCC 算法在非高斯噪声环境下具有更好的收敛速度、更低稳态误差。