基于NAR神经网络的船舶运动姿态短期预测∗

余缜 李军

（南京理工大学自动化学院 南京210094）

1 引言

随着经济和科技水平的发展，对于海洋的探索开发越来越多［1］，比如海洋运输、海底采矿、海上风力发电以及旅游观光等。船舶在海上航行或作业的过程中，不可避免地会受到风浪的扰动影响，导致船舶产生横摇、纵摇、艏摇、横荡、纵荡以及垂荡六个自由度上的运动。船舶六自由度运动给海上作业带来诸多不便和危险，比如，舰载武器的精确瞄准、直升机在船舶甲板的起降、船舶之间的货物运输以及航海摄影。如果能获得船舶运动状态，并进行短期预测，可以提升舰载设备的操作精确度，降低事故发生几率。

现在常用的方法是时间序列法，它的思想是利用过去一段时间内某事件时间的特征来预测未来一段时间内该事件的特征，自回归模型（Autore⁃gressive Model，AR模型）是构建时间序列的常用模型［3］，时间序列法的优点是不需要知道任何先验信息和船舶航态的状态方程，仅利用船舶本身的历史运动状态数据寻求规律，就可以进行船舶运动姿态的预测。

基于AR模型的预测属于线性预测的方法，然而，船舶的六自由度运动是一个复杂的非线性过程，使用线性预测法会有某些偏差。对于这个问题，NAR神经网络模型是一个更好的解决方案。

本文从船舶运动姿态的时间序列入手，分析了传统的AR模型预测法，再对船舶运动姿态建立了NAR神经网络模型，对船舶运动姿态进行预测。利用实际采集的船舶运动姿态数据对NAR神经网络模型进行训练，将训练结果用于预测仿真，使用同一批数据，分别利用AR模型和NAR神经网络模型进行预测，并将实验结果进行对比。

2 船舶运动姿态的时间序列分析

船舶的六自由度运动姿态可以看成是无数个具有不同波长，波幅与随机初始相位的余弦信号的叠加的运动过程，它的时间序列中包含着一些相关性信息。根据统计学知识，可以通过线性模型对船舶的运动规律进行拟合，从而达到预测未来状态的目的。

AR模型是时间序列分析法中针对平稳序列常用的一种线性模型，它的思想是通过对变量自身的历史数据的相关性进行研究，将这种关系进行量化处理，从而预测未来状态。AR模型的定义为

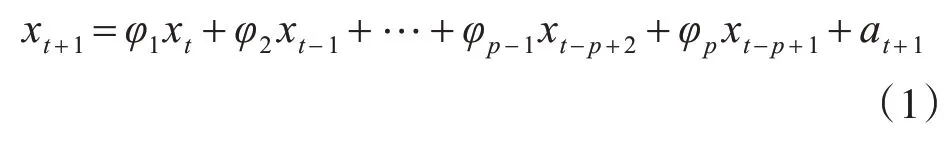
基于AR模型的预测算法如图1所示，主要包括模型参数估计，模型定阶和预测三部分内容。

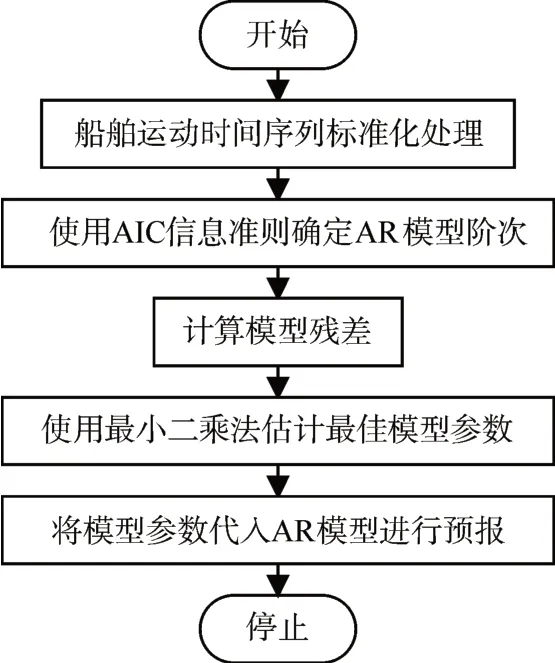
图1 基于AR模型预测算法流程图

AR模型是一种典型的线性时间序列模型，但是在实际的高变化应用下，时间序列的线性模型难以建立，或者预测精度不高［5］，因此，应该针对时间序列建立非线性模型。

3 NAR模型

人工神经网络（Artificial Neural Network，ANN）是一种由受生物神经系统启发的数学模型表示的神经网络，它是一种智能系统，可以识别时间序列模式和非线性特征，因此它已经被广泛应用到动态非线性时间序列建模［6］。

神经网络由若干神经元组成，这些神经元可以构成神经网络的不同层次，一般分为输入层、隐含层和输出层。神经元相互作用使神经网络具有强大的功能，神经网络理论的基础之一就是三层神经网络可以逼近任意函数，所以理论上，只要数据量足够大，神经元足够多，就可以通过调整神经元权值和阈值学到任意的东西［7］。

NAR神经网络是一种基于具有反馈连接的线性自回归模型的循环动态网络［8］，它常用于时间序列的多步预测，其结构如图2所示。NAR神经网络可由式表示，使用t时刻之前的d个值预测y(t)的值。f(·)是事先未知的，通过训练神经网络，调整各条链路的权重和偏差值来得到近似的f(·)。

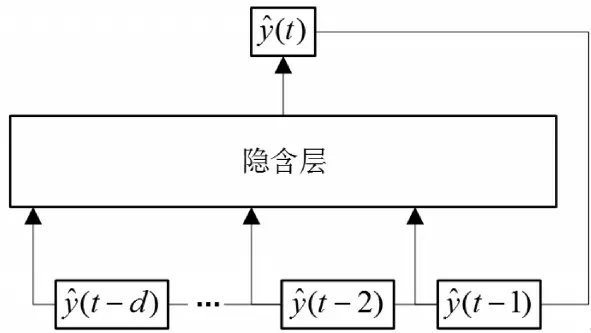
图2 NAR神经网络结构示意图

神经网络的训练过程实际上就是不断调整未知参数使得代价函数达到最小值，通常选择均方误差函数MSE作为代价函数，如式（3）所示：

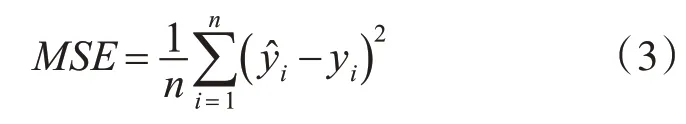
传统的用来更新参数的反向传播类型算法有最速下降法和高斯-牛顿法。

最速下降法［9］沿着梯度的反方向，按照一定的步长大小进行参数更新，使代价函数达到最小值，如式（5）所示：

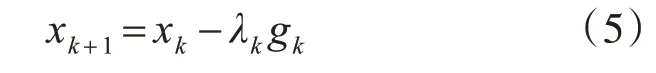
高斯-牛顿法［10］是在牛顿法的基础上得到的，仅用来解决非线性最小二乘问题。采用牛顿法求解式中F(x)的最小值，需要计算其梯度向量和Hessian矩阵。梯度向量如式（6）所示：

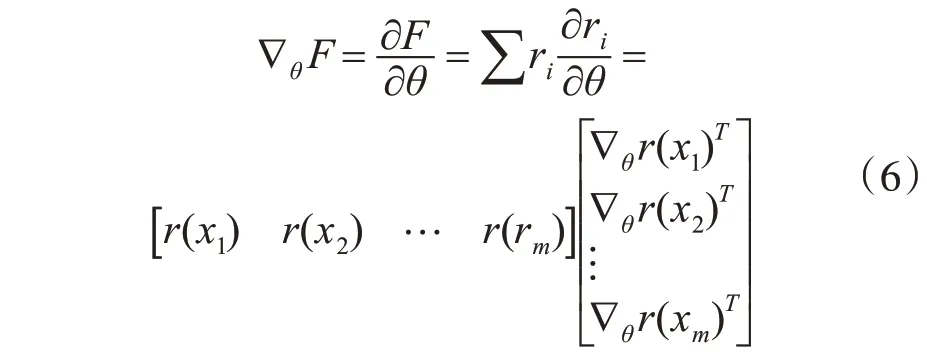
其中：

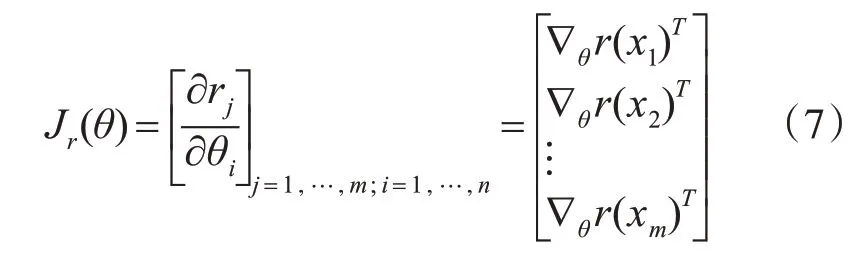
是r的Jacobian矩阵，则式（6）可以写作：

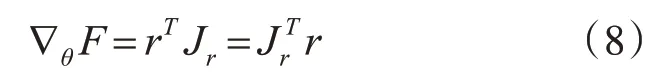
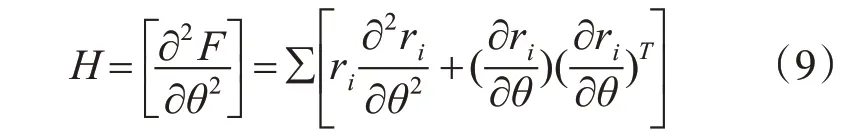
当残差ri≈0，时，可以认为二阶导数项接近于0而舍去，所以Hessian矩阵可以近似写为

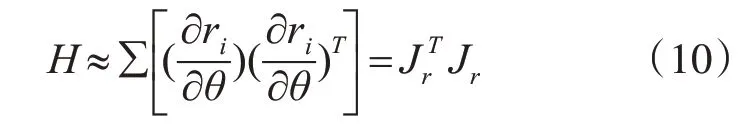
将梯度向量，近似Hessian矩阵代入牛顿法迭代公式：

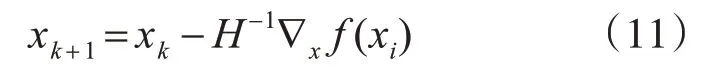
即可得到高斯-牛顿法的迭代公式：

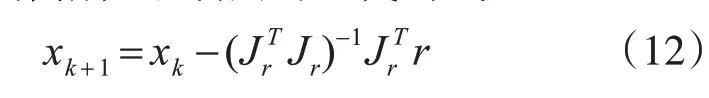
只需要计算Jacobian矩阵，而不需要计算二阶导数，简化了迭代步骤。高斯-牛顿法与牛顿法的缺点一样，当初始值距离最小值较远时，高斯-牛顿法并不能保证收敛，并且当近似奇异的时候，高斯-牛顿法也不能正确收敛［11］。

Levenberg-Marquardt算法［12~13］为了克服上述高斯-牛顿法的缺点，在高斯-牛顿法的基础上，改进迭代公式，通过在Hessian矩阵中加入阻尼系数来控制每一步迭代的步长及方向，Levenberg-Mar⁃quardt算法的迭代公式如下：

其中，λ是阻尼系数，记，当λ>0时，有如下效果：

1）λ比较大时，对角线元素占主导地位，，迭代算法会以较小的步长接近最速下降法；

2）λ比较小时，迭代算法接近高斯-牛顿法。高斯-牛顿法在误差最小值附近更快、更准确，适合迭代的最后阶段，非常接近最优解，避免最速下降的震荡。

因此，Levenberg-Marquardt算法的目标是尽快接近高斯-牛顿法，在每次迭代后，若性能函数减小，则减小λ，若在某次迭代中，性能函数增加，则增大λ，这样，在算法的每次迭代中，总是降低性能函数。

Levenberg-Marquardt算法结合了最速下降法和高斯-牛顿法的优点，基于Levenberg-Marquardt算法的神经网络训练算法通常是训练中等大小前馈神经网络的最快方法。因此在本文中，使用Lev⁃enberg-Marquardt算法对NAR神经网络进行训练。

4 数值仿真

在海上航行作业过程中，船舶六自由度运动中横摇角对船舶的稳定工作影响较大，故在本文实验中选取船舶的横摇角进行数值仿真，运动姿态时间序列通过在国家电投集团“电投01”风电运维船上安装传感器装置采集得到。

运用NAR神经网络模型对船舶运动姿态时间序列进行预测，本文选取时长200s的时间序列作为样本，采样频率为100Hz。将样本的前75%的数据作为训练数据，用来训练神经网络，后25%的数据作为测试数据，验证神经网络的预测性能。AR模型预测结果如图3所示，NAR模型的预测结果如图4所示，两种模型的预测误差对比如图5所示。

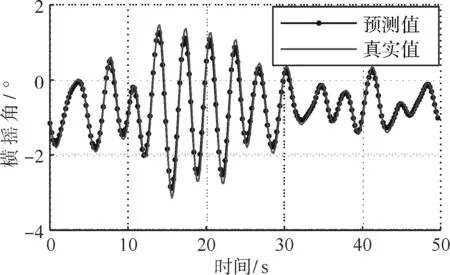
图3 AR模型预测结果

图4 NAR神经网络模型预测结果

图5 NAR神经网络模型预测误差

对于不同模型的预测性能，使用两个指标来衡量，均方根误差RMSE和决定系数R2。RMSE是MSE的平方根，可以保持指标和原始数据的量纲一致；决定系数R2用于度量因变量的变异种可由自变量解释部分所占的比例，以此来判断模型的解释力。

表1 表示了两种模型的预测性能分析结果。由表可知，NAR模型较传统的AR模型有更好的预测精度。

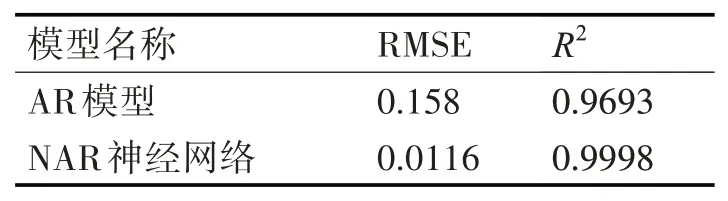
表1 船舶运动姿态预测结果性能分析

5 结语

本文从船舶运动姿态的时间序列分析入手，针对传统AR模型在船舶运动姿态预测上的不足，引入NAR神经网络模型，使用Levenberg-Marquardt算法训练神经网络，对船舶的横摇运动进行预测，结果表明，NAR神经网络模型比传统的AR模型预测精度更高，并且能充分逼近非线性映射，同时，该方法具有通用性，可以适用于船舶其他自由度上的运动预测，在工程上具有较高的使用价值。