深度研读教材策略之三:丰富数学知识的表现形式②
李凤仙 严敬 杨艳
【导读】
“用小数加减法解决问题”是对人教版小学数学四年级下册第六单元“小数加减法的运算定律”内容的实际应用。
对于加减法混合运算的“特殊规律”,教材中并没有明确地给出范例,但在学生的实际生活中却有着广阔的应用空间。本案例中,来自昆明市盘龙区金康园小学的李凤仙老师以“相差数”问题为载体,在生动形象的问题情境中,使学生轻松理解了加减混合运算中的一些“特殊规律”。赋予了数学知识丰富的表现形式,使学生对数学知识本质的理解更加深刻。
【案例】
课堂实录:
一、创设情境,唤起旧知
师(出示板贴图):妈妈身高1.6米,玲玲身高1.42米。妈妈比玲玲高多少米?你会解答吗?怎样列算式?
生1:1.6-1.42=0.18(m)。
师追问:为什么用减法?
……
(师板书:解决问题)
二、探究新知,建立模型
(一)初步感知
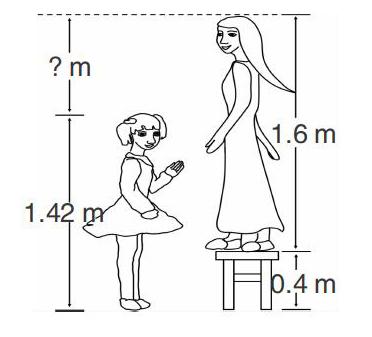
师(出示板贴图):妈妈站在一个0.4米高的凳子上,现在妈妈比玲玲高多少米?
生(独立解答并汇报):1.6+0.4=2.0(m),2.0-1.42=0.58(m)。
(二)深入理解
师:谁懂他的算法?说说他是先求什么?再求什么?
生:先求出妈妈站在凳子上的“假身高”,再用妈妈的“假身高”和玲玲的身高求出“假相差数”。
……
师追问:还有不同的算法吗?
生1:1.6-1.42=0.18(m),0.4+0.18=0.58(m)。
师:这又是怎么回事?谁懂他的算法是什么意思?
生2:他先求出玲玲和妈妈身高之间的实际相差数,再用实际相差数加凳子高度。
师追问:听懂了吗?
(部分学生表情疑惑)
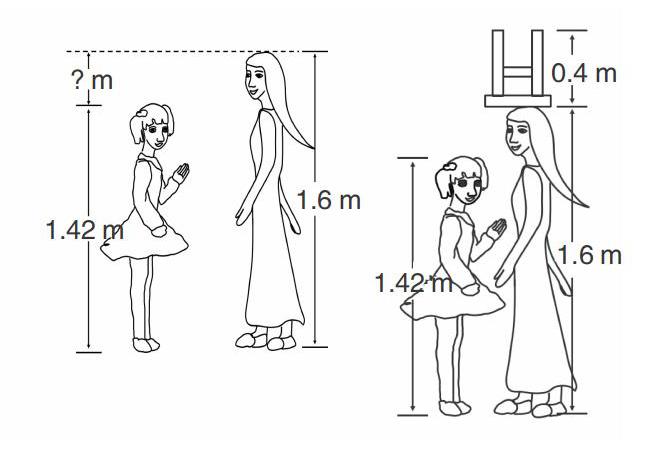
师(用图片演示):怎样摆能一眼看出“1.6-1.42=0.18(m)”?
生3:妈妈站在原地和玲玲比高(摆图片)。
师追问:不对呀?凳子呢?
生3(把凳子放到了妈妈头上)
(其余学生惊奇)
师:这样行吗?
生:不行!……行!
师:怎么一会儿说行?一会儿又说不行啊?
……
师:妈妈本来就比玲玲高,站到凳子上了就“高上加高”了,对吧?
生(齐):对!
师:那么无论是把凳子摆在脚下,还是摆在头上,都体现出了……
生(齐):高上加高!
……
师:第一种先求要比较的两个数,再求他们的相差数;第二种是先求两个数的相差数,再求相差数的和。
(三)感受变化
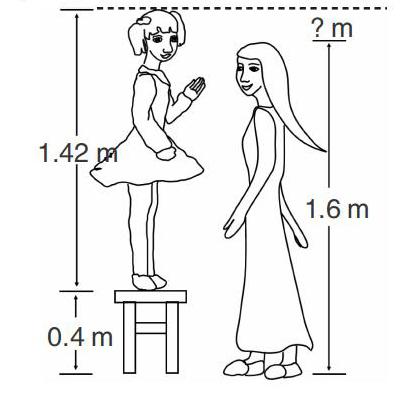
师(出示课件):玲玲站在一个0.4米高的凳子上,现在玲玲比妈妈高多少米?
(生独立完成后汇报)
师(展示第一种方法):1.42+0.4=1.82(m)
1.82-1.6=0.22(m)。
……
师:还有其他算法吗?
生3:1.6-1.42=0.18(m),0.4-0.18=0.22(m)。
师:谁懂他先算什么?再算什么?
生4:先算玲玲比妈妈身高矮0.18米,再用凳子的高度减去玲玲比妈妈矮的部分,就是玲玲比妈妈高的假相差数。
师:在第一个问题中,我们是用妈妈和玲玲的真实相差数加上凳子的高度,这回怎么变减了呢?
(生无语以对)
师(指着凳子放在妈妈头上的图):这一回能不能也……
生1(迫不及待):也可以先叫玲玲和妈妈公平比
较,再把凳子放到玲玲头上。
师(请学生1摆放好凳子):是这样吗?
生(齐):是。
师:刚才是妈妈比玲玲高了又高,而这一回是妈
妈比玲玲是怎么样呢?
生2:玲玲比媽妈“反败为胜”。
……
(还有部分学生不是很理解)
师:玲玲本来比妈妈矮,但现在比妈妈高了,是谁帮助玲玲长高了呢?
生(齐):凳子!
师:凳子一共帮玲玲长高了几次?
生:一次!……两次!
师:说两次的同学上来指指,长高了哪两次?
生(手指着板贴图):第一次长得和妈妈一样高,长了0.18米。第二次又涨了0.22米,这才是玲玲现在比妈妈高出来的高度。
……
师(总结):求两个数的相差数,如果其中一个数是发生变化的,可以先求出变化数的结果再比较;也可以先比较,再用变化数与相差数相加或者相减。
(四)总结回顾
师:这节课我们发现,所有小数加减法解决问题和整数加减法解决问一样,都要经过三个环节:
1.先读题目寻找确定要解决的问题→阅读与理解;
2.2.分析条件,选择算法,列式解答→分析与解答;
3.回顾总结解题方法→回顾与反思。
三、发散思维,巩固模型
师:根据下面信息,你能提出什么相差数问题?
……
师:老师也提出了一个问题:
妈妈身高1.6米,玲玲身高1.42米。妈妈站在一个0.6米高的凳子上,玲玲站在一个0.4米高的凳子上。现在谁高?比对方高出多少米?如果互换凳子呢?
这题留给大家课后思考,请大家参照本节课学会的求相差数方法尝试解决这个题。
四、全课总结,升华提高
师:其实生活中还有很多相差数问题,比如……
1.求“电信塔”顶端与“电力塔”顶端的高度相差多少米?
2.第五单元数学测试卷,小红扣了3分,小明扣了8分,谁的成績高?高多少分?
3.这个月妈妈的工资是5000元,爸爸的工资是6000元,妈妈发的奖金是900元,爸爸的奖金是300元。这个月谁的收入多?多多少元?
总结:希望大家将今天学会的新方法更好地应用到生活中去,解决更多相差数问题。
【思考】
“相差数”问题是小学数学解决问题中的一类重要问题,也是对学生进行“等量代换”数学思想渗透的重要途径。把小数加减法中一些“特殊规律”的应用和解决相差数问题结合起来,赋予它们丰富的表现形式,是这节课的特色所在。
通过学生喜闻乐见的生活事例来承载数学知识,使数学看起来不再那么冰冷;用丰富的表现形式从不同角度演绎同一个数学知识,使枯燥的数学展现多姿多彩的另一面。这就是这节课的价值所在:
1.一题多变,一题多练。两个人、一个小板凳,元素不多。“比身高”是生活中常见的趣事,深受学生喜爱。就在这样司空见惯的情境中,不多的元素通过巧妙的排列组合,却呈现了丰富的表现形式:一会儿是妈妈站在凳子上,一会儿是玲玲站在凳子上;一会儿是求相差高度,一会儿是求女儿身高,一会儿是求妈妈身高,一会儿是求凳子高度。学生一不小心就会坠入“迷魂阵”中,难寻来时路。但拨开云雾见青天才发现,路还是原来那条路。变化的是题目的外形,不变的是数学模型的基本框架。一题多变,一题多练,既节约了教学的成本,又最大限度地提高了学生的思维水平。何乐而不为呢?
2.不同的思路,就会有不同的算式。妈妈本来就比玲玲高,妈妈站在凳子上,现在比玲玲高多少呢?可以求出妈妈现在的“假身高”,再和玲玲比较相差数——这是常规解法,学生都能理解。通过板贴图的演示,学生也能深入理解到第二种解法:妈妈本来就比玲玲高了,再站上了凳子,现在就“高上加高”,所以要把实际的相差数与凳子的高度进行相加。同样是第二种解题思路,到了玲玲站在凳子上的时候,为什么变成相减了呢?这是这节课学生思维的一个“拐点”,也是教学的难点。通过板贴图的演示和老师富于儿童话的教学语言,学生终于明白了:玲玲原来比妈妈矮,要超过妈妈的话,要先“追”后“超”。所以小凳子的高度0.4米分为两部分:第一部分的0.18米是用来追上妈妈的,剩下的0.22米才是反超妈妈的。不同的思路,就会有不同的算式。同样的思路在不同的应用条件下,运算的“方向”也不同。老师虽然不刻意讲解“加减法混合运算中可以先加后减或先减后加”等运算定律,但相信学生早已了然于胸。
3.情境变了,数学问题还是原来那个“味道”。如果学生学会了“身高问题”就只会解决身高问题,那是数学教育的悲哀。怎样让学生“在新的情境中对学过的知识进行辨认、再现和应用?”这才是学生真正理解数学知识应该达到的水平。把“身高问题”变成山上与山脚下的高压线塔高度问题、考试的计分问题等,是对本节课所学数学模型的一个有效发散与变形。学生通过思考发现:数学问题的“样子”变了,但“味道”还是原来那个“味道”。
丰富的外在表现形式与简约的内涵表达,这就是数学课堂教学中矛盾与统一的辩证关系。在“变”中保持“不变”,在“不变”中求“变”,这是小学数学教师应该练就的强硬本领。

