宜昌城区短历时暴雨强度公式参数优化及暴雨雨型特征分析
张鹏宇 王振洋 张雅 曾令


摘要:基于历史降雨资料,采用数理分析方法,获得城市暴雨特征的量化表达,是城市风险管控、基础设施规划设计的关键性基础工作之一。根据宜昌城区短历时暴雨观测资料,应用遗传算法分别对皮尔逊-Ⅲ型频率分布曲线和暴雨强度公式参数进行了优化求解,通过趋势分析得到了近30 a的年际变化特征,采用芝加哥法分析确定了短历时暴雨雨型。结果表明:确定的宜昌城区暴雨强度满足精度要求;宜昌城區近30 a短历时暴雨的雨量峰值趋于增加,暴雨发生的历时主要集中在3 h以内。采用芝加哥法确定了重现期为2 a各降雨历时(步长取5 min)的设计暴雨雨型,雨峰位置的降雨强度随降雨历时的增加呈现出一定的上下波动,但各历时峰值在数值上相差并不明显。研究成果可为城市雨水径流控制等提供参考。
关键词:暴雨强度;雨型特征;参数优化;趋势分析;宜昌城区
中图法分类号:TV122.1文献标志码:ADOI:10.15974/j.cnki.slsdkb.2021.06.001
文章编号:1006 - 0081(2021)06 - 0008 - 04
1 研究背景
近年来,随着全球气候变化,极端暴雨事件越来越频繁[1],成为社会各界关注的焦点。宜昌市地处鄂西南丘陵山地,典型地形气候特征的暴雨时有发生。此外,近年来城市发展对区域水文循环产生的影响不容忽视,暴雨致涝问题日渐突出。城市暴雨内涝与强降雨密切相关,而短历时的强降雨是引起城市内涝的主要原因之一[2]。因此,研究宜昌城区短历时降雨强度、降雨历程等规律、特征及其变化情况,对于城市风险管控、基础设施建设都具有重要意义。
暴雨强度公式是基于历史降雨实测资料,采用数理分析方法获得的描述城市暴雨特征的定量表达,是城市排水系统等基础设施规划与设计的基础[3]。频率分布函数和强度公式参数优化是确定暴雨强度公式的重要环节,参数取值准确与否决定暴雨强度公式计算成果的参考价值。然而,上述模型均具有非线性的特点,《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》[4](下称“导则”)指出,基于历史降雨数据,通过数学优化计算是确定以上参数的有效途径。在我国应用最广泛的皮尔逊-Ⅲ型频率分布函数参数优化方面,矩法、权函数法、适线法等[5]最为常见。其中,矩法计算简单,但求解精度偏低,特别是当样本容量较小时,采用该方法获得的参数常常存在较大的偏差;基于权函数的优化方法本质与矩法相同,普通权函数法仅针对单参数优化问题,难以对皮尔逊-Ⅲ型频率曲线的多个参数进行联合优化,而双权函数法虽然在一定程度上提升了求解精度,但仍未从根本上解决精度不足的问题;适线法的求解精度对操作者的主观意志较为敏感,难以摆脱主观随意性的影响。在暴雨强度公式参数优化方面,最常见的方法是最小二乘法、高斯牛顿法[6],采用以上方法在优化过程中难以跳出局部最优解。近年来,随着计算机技术和仿生群智能优化算法的持续发展与进步,遗传算法[7-8]、人工蜂群算法[9]等方法被逐渐应用于暴雨强度公式参数确定中,效果较好。
为此,本文基于宜昌城区气象资料,采用遗传算法对皮尔逊-Ⅲ型频率分布函数和强度公式参数进行优化求解,推导出符合精度要求的暴雨强度公式,并对公式的计算精度进行验证。最后,对宜昌城区短历时暴雨雨型特征进行分析,研究成果以期为城市基础设施规划与设计提供参考。
2 基础资料与分析方法
采用长江水利委员会水文局三峡水文水资源勘测局宜昌蒸发站资料作为本文分析的基础资料,采用该站1990~2019年共计30 a暴雨自记雨量资料,根据年最大值法选取了每年10,30,60,180,360 min共5个历时的最大降雨值为暴雨强度公式编制样本。采用遗传算法分别对皮尔逊-Ⅲ型频率分布函数和暴雨强度公式参数进行优化求解,得到宜昌城区暴雨强度公式,在此基础上,采用芝加哥法[10]推求设计暴雨雨型,并对其特征进行分析。
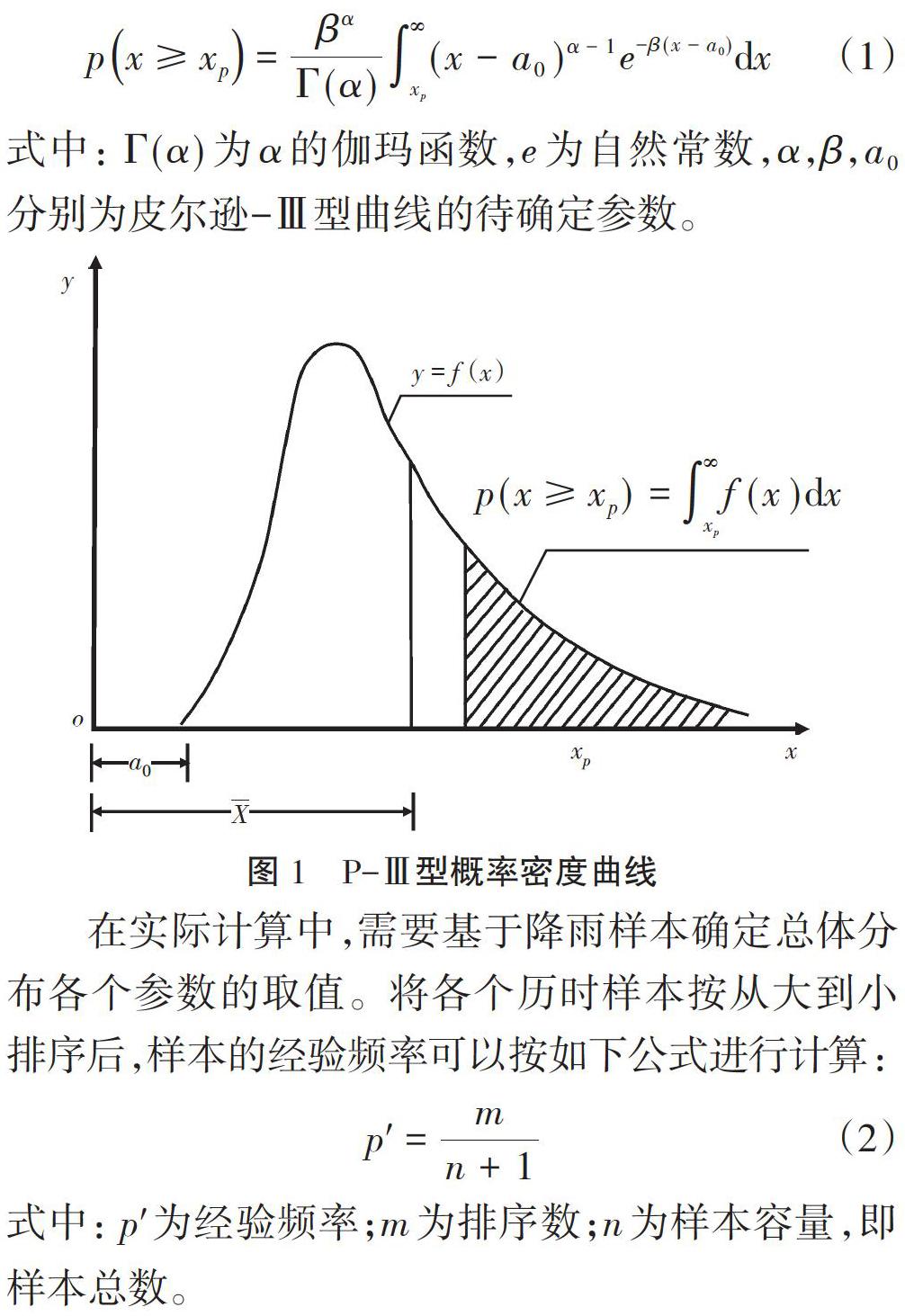
2.1 皮尔逊-Ⅲ型频率分布曲线参数优化原理
皮尔逊-Ⅲ型概率密度函数曲线如图1所示。降雨频率分析中需要对皮尔逊-Ⅲ型分布的概率密度函数进行积分:
在实际计算中,需要基于降雨样本确定总体分布各个参数的取值。将各个历时样本按从大到小排序后,样本的经验频率可以按如下公式进行计算:
确定经验频率后,通过一定策略不断调整皮尔逊-Ⅲ型分布函数中[α],[β],[a0]待确定的参数值,直至理论计算频率与经验频率之间的误差尽可能小时,对应的[α],[β],[a0]即为所求的参数值。由此,将参数估计问题转化成为非线性规划问题,可以建立如下优化目标函数:
得到频率分布函数后,即可获得当地重现期([P])、降雨强度([i])和降雨历时([t])之间的关系。
2.2 暴雨强度公式参数优化原理
暴雨强度公式描述了当地[P]-[i]-[t]之间的定量关系。由于不同地区的降雨存在不同程度的差别,因此,暴雨公式需要通过当地的降雨资料分析确定。根据导则,暴雨强度公式如下:
将暴雨强度公式参数估计问题转化成非线性规划问题,根据当地[P]-[i]-[t]之间的关系,以暴雨计算强度计算值[ik]与经验计算值[i′k]之间的绝对均方差建立目标函数:
式中: [ik]为第[k]项观测值的理论计算暴雨强度;[i′k]为第[k]项观测值的经验暴雨强度;[F]为暴雨强度理论计算值与经验值的误差平方和。
为确保暴雨计算值的可靠性,需要对获得的暴雨强度公式进行精度校验。根据导则规定,在一般降雨强度区域,当计算重现期为2~20 a时,暴雨强度计算值与经验值的平均绝对均方差宜控制在0.05 mm/min以内,平均相对均方差不宜超过5%。
式中: [X]为平均绝对均方根误差;[U]为平均相对均方根误差。
2.3 遗传算法原理
遗传算法[7-8]是一类仿自然界进化规律的随机搜索算法,在处理非线性模型参数优化的问题中表现出较强的通用性和可靠性。其基本思想是从一组随机初值产生的初始种群为起点,采用随机化的策略对在一个参数区间内实现高效寻优计算,从而获得问题的近似解,并以近似解的适应度来衡量解的优劣,然后,基于过程解的优劣程度,对种群进行选择、交叉和变异操作实现算法的遗传特性,使得近似解的质量演变朝着最优的方向进行,如此经历多次迭代计算,输出问题的最优解。
3 结果分析
3.1 皮尔逊-III型曲线参数优化结果
根据长江三峡水文水资源勘测局宜昌蒸发站1990~2019年(30 a)5个历时(10,30,60,180,360 min)暴雨雨量资料,按从大到小排序,得到各个历时30个暴雨样本数据。以式(3)为目标函数,采用遗传算法对各个历时的皮尔逊-III型分布曲线参数进行优化,优化结果如表1所示,相应的频率分布曲线如图2所示,可以看出,优化结果和经验频率拟合较好,说明获得的参数具有较高的可靠性。
3.2 暴雨强度公式参数优化结果
基于优化后的皮尔逊-III型概率分布曲线,得到宜昌城区降雨[P]-[i]-[t]之间的关系,以式(5)为目标函数,采用遗传算法对暴雨强度公式的参数进行优化,最终获得宜昌城区暴雨强度公式:
按照式(8)求得在重现期为2~20 a时的平均绝对均方根误差为0.042 [mm/min],小于0.05[ mm/min],平均相对均方根误差为3.16%,低于5%;以上均满足精度要求。
3.3 短历时暴雨特征分析
3.3.1 年际变化特征
从宜昌城区逐年雨量资料中选择1990~2019年历时为10,30,60,180 min和360 min的年最大降雨量值进行统计分析,各个历时年最大降雨量的变化趋势见图3~4。近30 a宜昌城区各历时最大降雨量波动较大,其中,10,180 min和360 min年最大降雨量分别以2.52,2.99,3.10 mm/10 a增加,增加趋势较为显著;30 min和60 min年最大降雨量变化趋势无确定性规律,仅表现为周期性波动;总体而言,近30 a宜昌城区短历时暴雨的雨量峰值趋于增加。图4结果显示,180 min和360 min年最大降雨量序列吻合程度较高,说明近30 a宜昌城区短历时暴雨发生的历时主要在3 h以内。
3.3.2 设计雨型特征分析
基于前文获得的宜昌城区暴雨强度公式,采用芝加哥法分析确定其短历时暴雨雨型。根据现有研究,宜昌城区综合雨峰位置系数r取0.28[11]。计算步长设定为5 min,计算得到重现期为2 a时各降雨历时的峰值、雨峰时段汇总如表2所示,以及短历时降雨强度及累计降雨量,如图5~6所示。由表2可知,宜昌城区短历时暴雨的设计雨型为单峰型,随着降雨历时的增加,雨峰时刻对应的降雨强度呈现出上下波动变化。其中,降雨历时为30,60 min和90 min的峰值分别发生在第2、第4和第6时段,位于整个降雨历程的1/3分位;降雨历时120,150 min和180 min的峰值分别发生在第7、第9和第11时段,位置略超前于整个降雨历程的1/3分位。雨峰处降雨强度虽表现出一定的波动,从图5来看,不同历时峰值差异相对较小。由图6可知,重现期为2 a时,历时为30 min的降雨累积雨量呈现出“剧烈-平缓”的增长趋势,而历时为60~180 min的降雨累积雨量呈现出“平缓-剧烈-平缓”的增长趋势,且首段平缓发展时间随降雨历时增长而延长。
4 结 论
(1)遗传算法用于宜昌城区皮尔逊-Ⅲ型频率分布曲线和暴雨强度公式参数优化,实现了以上模型多个参数的联合识别,得到了宜昌城区暴雨强度公式。误差分析结果表明,本文确定的宜昌城区暴雨强度公式满足精度要求,同时表明遗传算法对于各类非线性模型参数的优化具有较强的适用性。
(2)宜昌城区近30 a短历时暴雨的雨量峰值趋于增加,暴雨发生的历时主要集中在3 h以内。
(3)基于宜昌城区暴雨强度公式,采用芝加哥法确定了重现期为2 a各降雨历时(步长取5 min)的设计暴雨雨型。结果表明:雨峰位置的降雨强度随降雨历时的增加呈现出一定的上下波动,但各历时峰值在数值上相差并不明显。重现期为2 a时,历时为30 min的降雨累积雨量呈现出“较快-缓慢”的增长趋势,而历时为60~180 min的降雨累积雨量呈现出“缓慢-较快-缓慢” 的增长趋势,且首段平缓发展时间随降雨历时增加而加长。
参考文献:
[1] 马京津, 李书严, 王冀. 北京市强降雨分区及重现期研究[J]. 氣象, 2012,38(5):569-576.
[2] 刘立军, 程玉祥, 吴益. 浙江省城市暴雨计算方法的比较研究[J]. 人民黄河, 2013,35(5):30-32, 35.
[3] 任雨, 李明财, 郭军, 等. 天津地区设计暴雨强度的推算与适用[J]. 应用气象学报, 2012,23(3):364-368.
[4] 住房和城乡建设部, 中国气象局. 城市暴雨强度公式编制和设计暴雨雨型确定技术导则[S]. 2014.
[5] 刘俊, 周宏, 鲁春辉, 等. 城市暴雨强度公式研究进展与述评[J]. 水科学进展, 2018,29(6):898-910.
[6] 周绍毅, 罗红磊, 苏志, 等. 南宁市新一代暴雨强度公式与暴雨雨型研究[J]. 气象研究与应用, 2017,38(2):1-5.
[7] 林林, 樊建军, 杨贵春, 等. 遗传算法在暴雨强度公式优化问题中的应用及Matlab实现[J]. 水利与建筑工程学报, 2008(4):30-32.
[8] 毛明策, 吴素良, 范婧儿. 基于遗传算法的暴雨强度公式参数计算[J]. 陕西气象, 2020(4):50-52.
[9] 杨一叶, 王志刚, 夏慧明. 人工蜂群算法在暴雨强度公式参数优化中的应用[J]. 价值工程, 2013,32(23):261-262.
[10] 戴有学, 王振华, 戴临栋, 等. 芝加哥雨型法在短历时暴雨雨型设计中的应用[J]. 干旱气象, 2017,35(6):1061-1069.
[11] 成丹, 陈正洪, 方怡. 宜昌市区短历时暴雨雨型特征[J]. 暴雨灾害, 2015,34(3):249-253.
(编辑:李 晗)

