采用奇异值分解和信息增益的树突状细胞模型

杨信民，董红斌，谭成予，周 雯

1.武汉大学 国家网络安全学院，武汉 430072

2.武汉大学 计算机学院，武汉 430072

人工免疫系统是模拟人体免疫系统工作机理的计算机免疫系统[1]，包括反向选择、危险理论、克隆选择、免疫网络等理论分支[2]，由于继承了免疫系统的生物智能特性，人工免疫系统被广泛应用于机器学习[3]、优化计算[4]、入侵检测[5]、异常检测[6]、故障检测[7]等领域。最新的免疫学理论称为危险理论（Danger Theory，DT）[8]。根据DT 的思想，从树突状细胞（Dendritic Cell，DC）的行为特征中获得的启发导致了称为DCA的免疫算法的发展[9]。

DCA是受生物危险理论启发，模拟DC生物机制的人工免疫算法，用于对人体内危险抗原的最初识别。但DCA 从本质上还是属于先天性免疫范畴，在设计之初就没有过多的考虑适应性。在实际的应用中如何将输入的特征映射到具体的信号特征，存在着严重依赖人工经验的问题，始终没有一个统一的、一般性的方法，严重影响DCA的适应性。

SVD能将原数据集规约成最相关特征子集，且能最大限度地保留分类信息，减弱数据混乱给算法带来的影响，然后根据IG得到最相关特征子集中的最相关特征，自适应地提取信号。根据以上特征，本文在DCA 的基础上，结合SVD 和IG 的思想，改进了DCA 算法中数据预处理和信号选择的部分，建立了一个基于SVD 和IG的树突状细胞模型——SIDCA，并将SIDCA 与经典DCA，优化版本的dDCA进行了比较。

1 相关工作

1.1 树突状细胞算法

1994年，生物免疫学家Matzinger提出了DT[8]，认为免疫系统是感知机体组织内的潜在危险，所有引发危险的抗原才是免疫识别的对象，而那些没有引发危险的抗原，免疫系统不会做出免疫反应。

DC 能够对采样到的多种生物信号进行融合、分析并转换为输出信号，然后根据输出信号的浓度从机体组织迁移到淋巴系统中，将采集到的抗原信息提呈给淋巴细胞，以此激活淋巴细胞来处理潜在的危险。

借鉴DT的思想和DC的行为特征，Greensmith等人在2005 年提出了DC 的人工抗原提呈模型及DCA[9]。随后，Greensmith 团队针对原DCA 算法参数较多、随机性太强的问题提出了dDCA[10]，简化了算法中所使用的信号，使得算法参数可控。为了提高DCA 的可用性和通用性该团队还提出了hDCA[11]，采用Haskell函数编程语言描述和规范DCA 算法。Gu 和Greensmith 提出了PCA-DCA[12]，采用PCA方法处理抗原数据，实现输入信号的自动分类；Chelly 提出了基于粗糙集、模糊集的DCA 算法[13-14]，实现信号特征自动选取和分类，提高了DCA算法在信号定义上的自适应性。

DCA 已经成功应用于诸多计算机安全相关的领域，解决了常见的异常检测问题，包括端口扫描检测[15]、僵尸网络检测[16]、机器人安全分类器[17]、ping 扫描检测[18]、服务器攻击检测[19]、服务器异常检测[20]、电网攻击检测[21]等；近年来也被应用于地震预测[22]、网络水军检测[23]等领域。

1.2 奇异值分解

SVD 能够用小得多的数据集来表示原始数据集，即可以将SVD看成是从噪声数据中抽取相关特征。文献[24]用SVD 降维提高了反向传播神经网络用于文件分类的性能。在文献[25]中，提出了基于奇异值分解的特征选择算法，并将算法与11 个常用特征选择算法在统一的评判标准下进行对比，结果显示，奇异值分解可以用于特征选择算法并有很高的精确度。

SVD定义为：

其中，M是一个m×n阶矩阵，U是m×m阶酉矩阵，U的列组成一套对M正交“输入”或“分析”的基向量，这些向量是MMT的特征向量；VT是V的共轭转置，是n×n阶酉矩阵，V的列（columns）组成一套对M的正交“输出”的基向量，这些向量是MTM的特征向量；Σ是半正定m×n阶对角矩阵，其对角线上的元素即为M的奇异值。

在之前研究中，DCA 错误的分类常发生在过渡边界。因此，当环境连续多次变化时DCA 会产生更多错误。SIDCA 采用SVD 产生相关子集，减弱数据混乱带来的影响。

1.3 信息增益

香农在1948 年提出了“信息熵”的概念，它具有量化信息的能力[26]。设X是一个取有限值的离散型随机变量，概率分布为：

则随机变量X的熵为：

设有随机变量(X,Y)，其联合概率分布为P(X=xi,Y=yj)=pij,i=1,2,…,n,j=1,2,…,m。

条件熵（conditionalentropy）H(Y|X)表示随机变量X的条件下随机变量Y的不确定性。

基于以上对信息熵的理解，出现了信息增益的概念[27]。设特征A对训练集D的信息增益为g(D,A)，则：

信息增益可以视为某个特征带给整个系统的信息量。在DCA 中，不同信号对算法最终分类结果的影响比重不同。借助信息增益，能够根据不同信号对分类结果影响程度的不同，自适应地去提取信号。

2 基于奇异值分解的树突状细胞模型

2.1 模型框架

该模型共有四个模块：基于奇异值分解的数据预处理模块、基于奇异值分解和信息增益的信号选择模块、信号处理模块和分类模块。图1 展示了基于奇异值分解的树突状细胞模型。

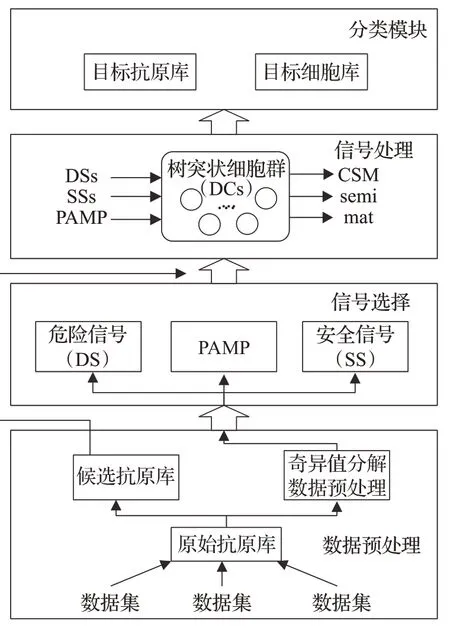
图1 改进的树突状细胞模型Fig.1 Improved dendritic cell model

模型从实际应用环境中获得所有特征建立原始抗原库，采用奇异值分解对数据进行降噪处理，并对特征进行降维操作，将所有特征映射到树突状细胞算法所需要的维度中。

接着，对降维后的数据集进行信号选择，采用基于信息增益的方法自适应地提取病原体相关模式分子信号（Pathogen-Associated Molecular Patterns，PAMP）、危险信号（Danger Signal，DS）以及安全信号（Safe Signal，SS）。当树突状细胞成熟时，通过累积输出信号浓度来确定抗原环境。

在最后的分类模块，通过每次累积的数据，计算环境评估的度量值MCAV，来确定当前的抗原环境是正常还是异常。

2.2 算法流程

2.2.1 数据预处理阶段

在数据预处理阶段的主要目的是将数据集（假设数据集已经将非数值型处理为数值型）降噪和降维，并使算法处理过的数据集能正确地被信号选择阶段的算法接收和处理。数据预处理算法的伪代码如下所示：

算法1数据预处理算法

一般数据集可视为一个二维矩阵。假设将目标数据集视为矩阵M，M为m×n阶矩阵。设矩阵M任意位置的值为vali,j，每列属性最大值为max，最小值为min，此阶段矩阵由以下公式进行标准化：

再由奇异值分解的定义：

奇异值分解去除噪声的一个典型的做法是保留矩阵中90%的信息，为了计算信息总量，将Σm×n中所有的奇异值求其平方和，即：

初始化K为2，若前K个奇异值累加不足信息总量的90%，则将K值加1，直到将奇异值的平方和累加到总值的90%为止。此时得到了保留信息总量90%的去除噪声的数据集，即：

原矩阵的密集总结矩阵T为原矩阵描述性数据子集，定义为：

2.2.2 信号选择阶段

用公式（3）对矩阵T进行数据标准化，接下来将整个矩阵T视为数据集D，|D|为数据集的样本容量。设有K个类Ck，k=1,2,…,K，|Ck|为属于类Ck的样本个数。设数据集D的某个特征A有n个不同的取值{a1,a2,…,an}，将D划分为n个子集D1,D2,…,Dn，|Di|为Di的样本个数。记子集Di中属于类Ck的样本集合为Dik，|Dik|为Dik的样本个数。

计算数据集D的经验熵H(D)：

根据公式（4）计算信息增益g(D,A)。最后根据信息增益将特征从大到小进行排序得到排序后的矩阵T′，求得信息增益最大特征列的均值mean。

算法2信号选择算法

其中pamp、ds、ss分别代表PAMP、DS、SS。

2.2.3 信号处理阶段

信号处理阶段算法接收上一阶段得到的各种信号，并输出成熟信号（Mature Signal，mat）、半成熟信号（Semi-Mature Signal，semi）以及协同刺激分子信号（Co-Stimulatory Molecules，CSM）。CSM通过DC的迁移阈值（migration threshold）来判断iDC 向半成熟或成熟状态分化，若累积的CSM大于DC 的迁移阈值则iDC 开始分化。设迁移阈值为mThreshold，信号处理算法的伪代码如下所示：

算法3信号处理算法

算法实现过程中，关键步骤是采集抗原的PAMP、SS和DS通过权值矩阵来进行信号融合生成CSM、semi和mat输出信号。权值矩阵如表1所示。

表1 权值矩阵的各项参数Table 1 Parameters of weight matrix

权值矩阵是多次实验后得出的经验参数，具体实现过程中可针对不同用途定义为不同值。信号处理公式如下：

Wp、Ws、Wd分别代表PAMP、SS、DS 对应的权值，IC为炎症细胞因子（Inflammatory Cytokines，IC），其功能是用来放大其他信号，本实验中暂未用到这一信号。

2.2.4 分类阶段

分类阶段算法对DC 迁移之后进行累积输出信号评估，设Am为此抗原被标记为成熟的次数，As表示此抗原被标记为半成熟的次数。分类阶段的伪代码如下所示：

算法4分类阶段算法

树突状细胞算法根据成熟环境抗原值（Mature Context AntigenValue，MCAV）来确定抗原的异常程度，MCAV的计算方式如下：

当MCAV大于指定的异常阈值时，则表示此抗原为异常，反之则此抗原为正常。MCAV的阈值一般为数据集中异常抗原实际所占比值。

3 实验与分析

3.1 实验设计

进行实验的两个数据集为：（1）UCI Wisconsin Breast Cancer dataset（WBC），由700 个数据实例组成，每个实例有9个标准化属性，代表潜在癌细胞的各种特征。第10个属性为类1或类2的分类标签。此数据集按种类排序，为有序数据集。（2）KDD99的一个子集，每个实例有32 个标准化属性，第33 个属性为分类标签。由于DCA对大型数据集的处理过程过于缓慢，本文所使用的是原数据集按照比例随机抽取的5 000条数据。此数据集经过多次随机打乱，为无序数据集。

在所有对比实验中DC 总数都被设置为100，在每次循环中对10个DC取样。

3.2 实验结果与分析

3.2.1 评价指标说明

本实验所使用的模型评价指标如表2所示。

表2 实验评价指标Table 2 Experimental evaluation indicators

3.2.2 在有序数据集上的实验

在有序数据集WBC 上，SIDCA 在真正类率、召回率、特异度、AUC、AVG和准确率均高于其他两种算法；真负类率略低于dDCA 算法，但高于DCA；SIDCA 有更低的漏报率；算法耗时SIDCA 与DCA 相近，远低于dDCA。从AUC 以及ACC 对比图可以更明确地看出，本文提出的SIDCA 不仅能够自适应地提取信号，在有序数据集上比进行对比的两种算法有更好的表现。实验结果如表3～表5和图2、图3所示。

表3 WBC数据集10次实验结果平均值对比Table 3 Comparison of average effects of 10 executions in WBC dataset %

表4 WBC数据集50次实验结果平均值对比Table 4 Comparison of average effects of 50 executions in WBC dataset %

表5 WBC数据集100次实验结果平均值对比Table 5 Comparison of average effects of 100 executions in WBC dataset %

图2 在WBC数据集100次实验AUC对比图Fig.2 Comparison of AUC values of 100 executions in WBC dataset

图3 在WBC数据集100次实验ACC对比图Fig.3 Comparison of ACC values of 100 executions in WBC dataset

3.2.3 在无序数据集上的实验

在KDD99 数据集上，SIDCA 在真正类率、真负类率、召回率、马修斯相关系数、AUC、AVG和准确率上均强于DCA 和dDCA；在特异度上SIDCA 略低于dDCA，但高于DCA；SIDCA有更低的漏报率；算法耗时SIDCA略高于DCA，远低于dDCA。从AUC 以及ACC 对比图可以更明确地看出，本文提出的SIDCA 不仅能够自适应地提取信号，在无序数据集上也有比进行对比的两种算法有更好的表现。实验结果如表6～表8 和图4、图5所示。

图4 在KDD99数据集100次实验AUC对比图Fig.4 Comparison of AUC values of 100 executions in KDD99 dataset

图5 在KDD99数据集100次实验ACC对比图Fig.5 Comparison of ACC values of 100 executions in KDD99 dataset

表6 KDD99数据集10次实验结果平均值对比Table 6 Comparison of average effects of 10 executions in KDD99 dataset %

表7 KDD99数据集50次实验结果平均值对比Table 7 Comparison of average effects of 50 executions in KDD99 dataset %

表8 KDD99数据集100次实验结果平均值对比Table 8 Comparison of average effects of 100 executions in KDD99 dataset

4 结束语

本文提出了基于奇异值分解的树突状细胞模型，该算法结合奇异值分解以及均方误差和信息增益，使得信号提取的过程不再需要人工经验，能够自适应地提取PAMP、DS以及SS。实验表明，不论是有序数据集还是无序数据集，本文提出的SIDCA 有效地提高了算法的精确度，减少了误报率，且受数据顺序的影响更小。

受到DCA 本身对无序数据处理能力不强、且DCA和SVD 均只适合于微型和小型数据集的制约，SIDCA在无序数据集和大型数据集的表现还不够优秀，下一步的研究目标是继续提高该算法在无序数据集上的精确度，采用并行算法提高该算法在大型数据集上的运算效率。进一步降低算法中的其他参数对人工经验的依赖，提高算法的普适性。并将SIDCA运用在计算机安全或疾病预测等领域。