基于激光三角法的圆柱度误差评定研究
刘悦雷,刘劲涛,张 陈
(沈阳工程学院a.研究生部;b.机械学院,辽宁 沈阳 110136)
随着能源电力现场零部件对检测技术要求的提高,采用接触探针式的传统测量方法的局限性逐渐显现。对于由软性材料组成的高精度表面,该方法不仅会对工件表面造成划伤,也会对测量的精度造成一定的影响[1],而激光三角法以非接触、无测量力、自动化程度高、测量范围大等优点,广泛应用于检测领域[2-3]。要实现物体三维形貌测量、形位误差评定及后续加工或修复工作,首先要利用各种测量设备并选择合理的测量方法对三维模型的表面数据进行采集,然后建立适用于圆柱度的误差评定数学模型及算法,最后对数学模型进行误差评定,确定形貌测量误差,为后续加工工序或修复提供数据支持。
1 测量系统的原理及坐标变换
1.1 测量系统的原理
激光三角法可将含有位移测量值的光信号转换为电信号,经计算机识别处理,为后续工作提供数据支持。由于测量时的入射光线和反射光线构成了一个三角形,所以被称为激光三角法[4],主要由激光器、透镜、成像屏和后续信号处理电路组成,如图1所示,封装好的激光三角测量仪如图2所示。
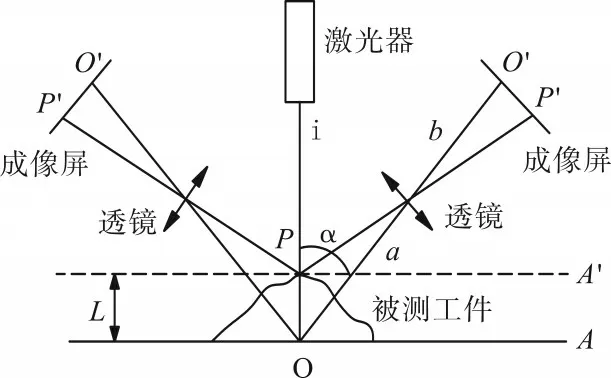
图1 激光三角法原理

图2 激光三角测量仪
激光器的光束i照射在被测工件上的P点,再经过物体表面折射,通过透镜投射到成像屏上的P'点。O点是激光束与参考平面A 的交点,O'点是O点经过透镜的像点。a为透镜的物距,b为透镜的像距,A'表示物体被测平面。P点距参考平面A 的距离L为
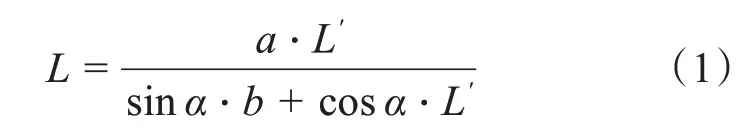
式中,L′表示成像点P′和O′的距离;a和b是固定参数。
1.2 坐标系的建立与转换
为了保证激光位移传感器的测量精度,必须把测头的安装误差控制在一定范围内,这就需要对测头的安装位置进行标定。将激光探头安装在测量机的Z 轴上,测量完成后需要将点激光测头(Point Laser Sensor,PLS)的测量值从自身坐标系转换到基准坐标系下,转换过程中所涉及的坐标系如图3所示。
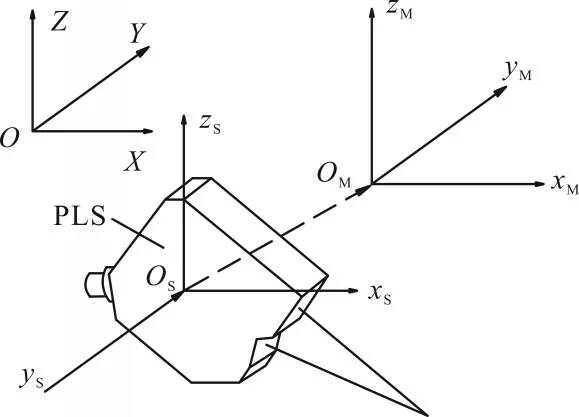
图3 坐标变换坐标系
1)建立激光测量D的设备坐标系O-XYZ,此坐标系下的坐标原点为光栅尺的0 位,导轨方向分别对应坐标轴的三个方向。
2)建立点激光测头的测量坐标系OS-xsyszs。PLS 坐标系的原点是测量值为0 的点,坐标轴的三个方向分别对应X轴、Y轴和Z轴。
3)建立机器坐标系OM-xMyMzM。测量机回零,并调节PLS测量值为0,将此点作为坐标系的原点,坐标轴的方向与激光测头的坐标轴方向一致。
将激光三角法的测量值从激光测头坐标系变换到机器坐标系中,采用齐次坐标来表示其变换过程:
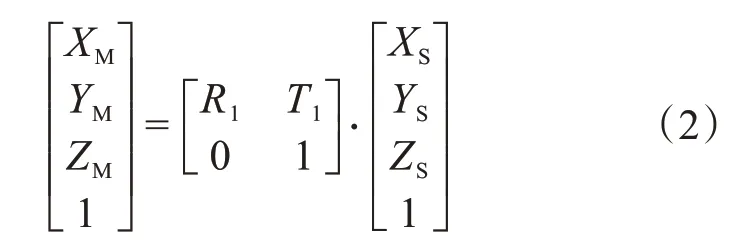
在OS-xsyszs坐标系中,假设激光束的单位向量分别用a、b、c表示,激光位移传感器的读数为l(l为激光束长度),则[alblcl]T就等于式中的[XSYSZS]T,[XSYSZS]T为PLS 坐标系OS-xs yszs的测量值。旋转矩阵A1 和平移矩阵B1 将[XSYSZS]T从OS-xsyszs坐标系转换到OM-xMyMzM,三坐标光栅值读数为(xM0,yM0,zM0)。
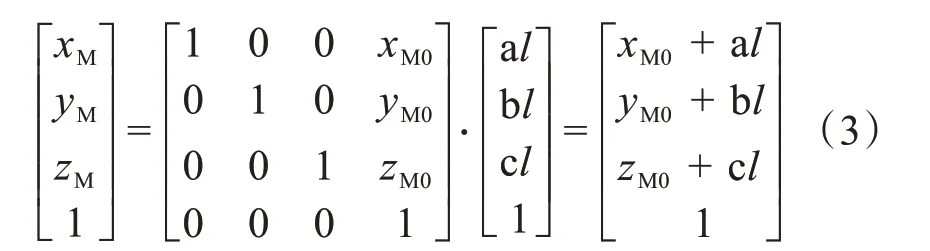
将A1、B1和[alblcl]T代入到式(3)中,便可把PLS 测量值从OS-xsyszs坐标系转换到OM-xMyMzM坐标系,即可获得PLS 激光束在三个坐标系下的转化。
2 圆柱度误差数学模型及评定算法
本文分别采用最小二乘法[5-6]和最小区域法[7]建立圆柱度误差数学模型并选择合适的算法进行误差评定。
2.1 圆柱度误差数学模型
圆柱度误差的评定原理如图4所示。
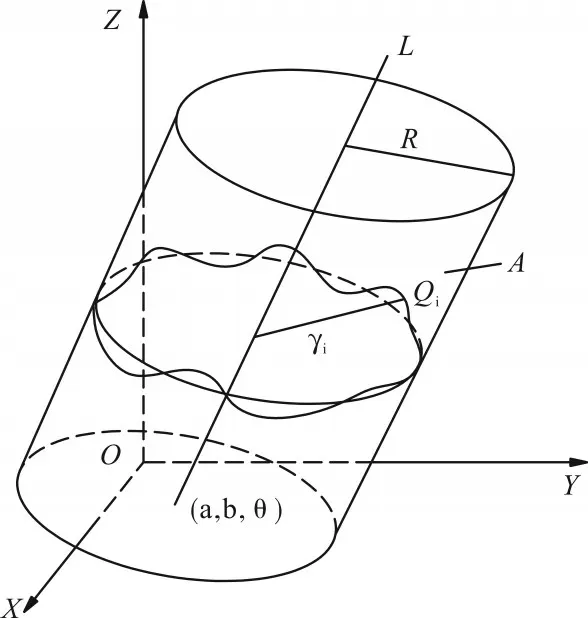
图4 圆柱度误差的评定原理
设参考圆柱面为A,横截面半径为R,轴线为直线L,实际圆柱面上的采样点坐标为Qi(xi,yi,zi),则采样点Qi到参考圆柱面轴线的距离为γi,设轴线L的方程为
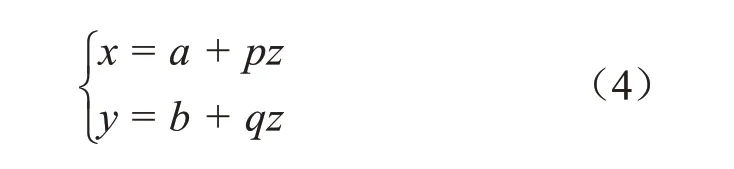
则有
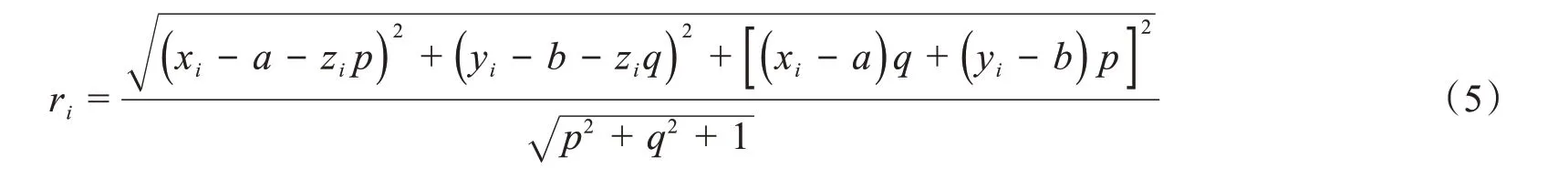
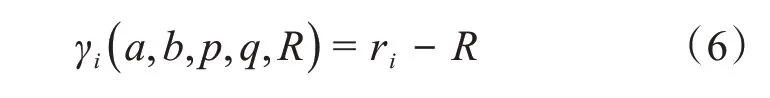
依据形状误差定义可知圆柱度误差为
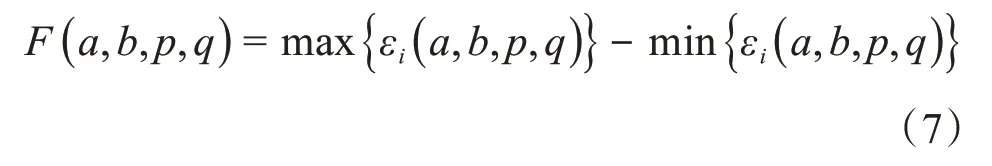
2.2 最小二乘评定法
以被测实际表面的最小二乘圆柱面为参考圆柱面,进行圆柱度误差评定的方法叫做最小二乘评定法。根据最小二乘法原理,选择一个圆柱体的轴线作为最小二乘轴线,同时也作为该圆柱体的基准轴线。根据该轴线建立两个可以将实际圆柱体包含的理想圆柱面,外侧圆柱体半径减去内侧圆柱体半径所得数值即为实际圆柱体的圆柱度误差[8]。
依据最小二乘原理:
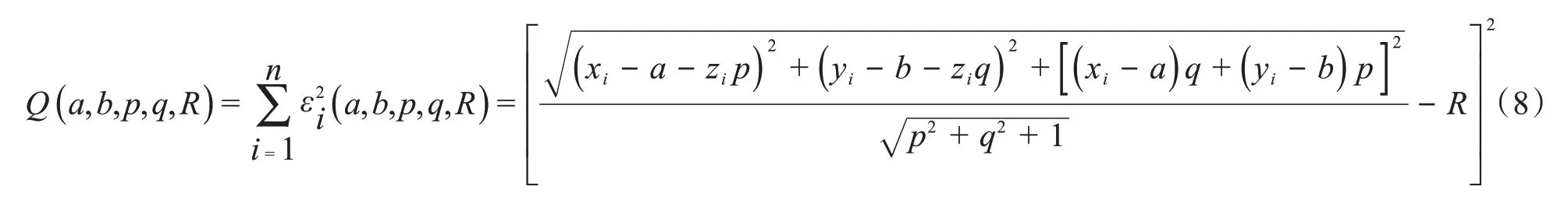
设(a*,b*,p*,q*,R*)为式(9)取得最小值的解:
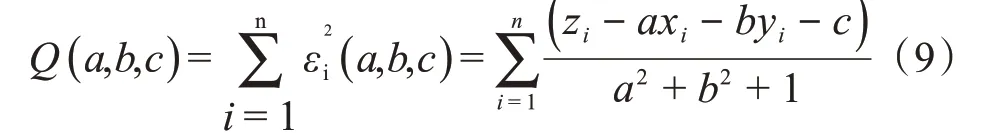
则将(a*,b*,p*,q*)代入式(10)即可得到最小二乘法评定下的圆柱度误差fLS:
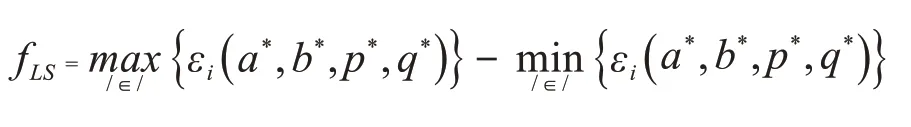
2.3 最小区域法评定
首先,建立满足最小条件的圆柱面作为参考,其轴线作为基准轴线;然后,根据基准轴线建立两个同轴的圆柱面,将实际圆柱面包含在内,则大圆柱面的半径R减去小圆柱面的半径r所得差值就表示圆柱度误差[9]。
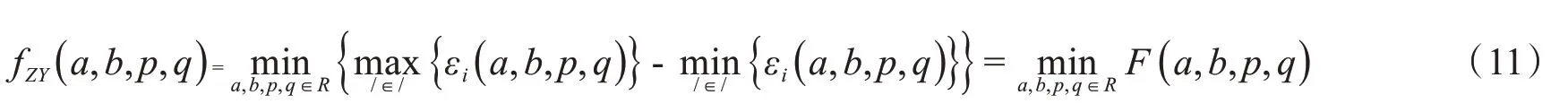
按圆柱度误差评定法的要求,函数fZY(a,b,p,q)需取最小值。
设[a*,b*,p*,q*]T为满足最小条件的参数,其极小值fZY(a,b,p,q)为该算法下的圆柱度误差值,记为FZY。
3 数据采集及误差评定
为了验证激光三角法测量圆柱度误差的可靠性,采用激光三角法与三坐标测量机测量法对试件的数据进行采集,对测量数据进行最小二乘法误差评定和最小区域法误差评定。
3.1 数据采集
测量1 个直径φ为30 mm 的圆柱体试件,选取3个不同截面,每个截面之间的距离为10 mm,在每个截面上按角度等分为12 个点,分别利用三坐标测量机和激光测量系统对其进行测量,获得圆柱度误差数据如表1和表2所示。
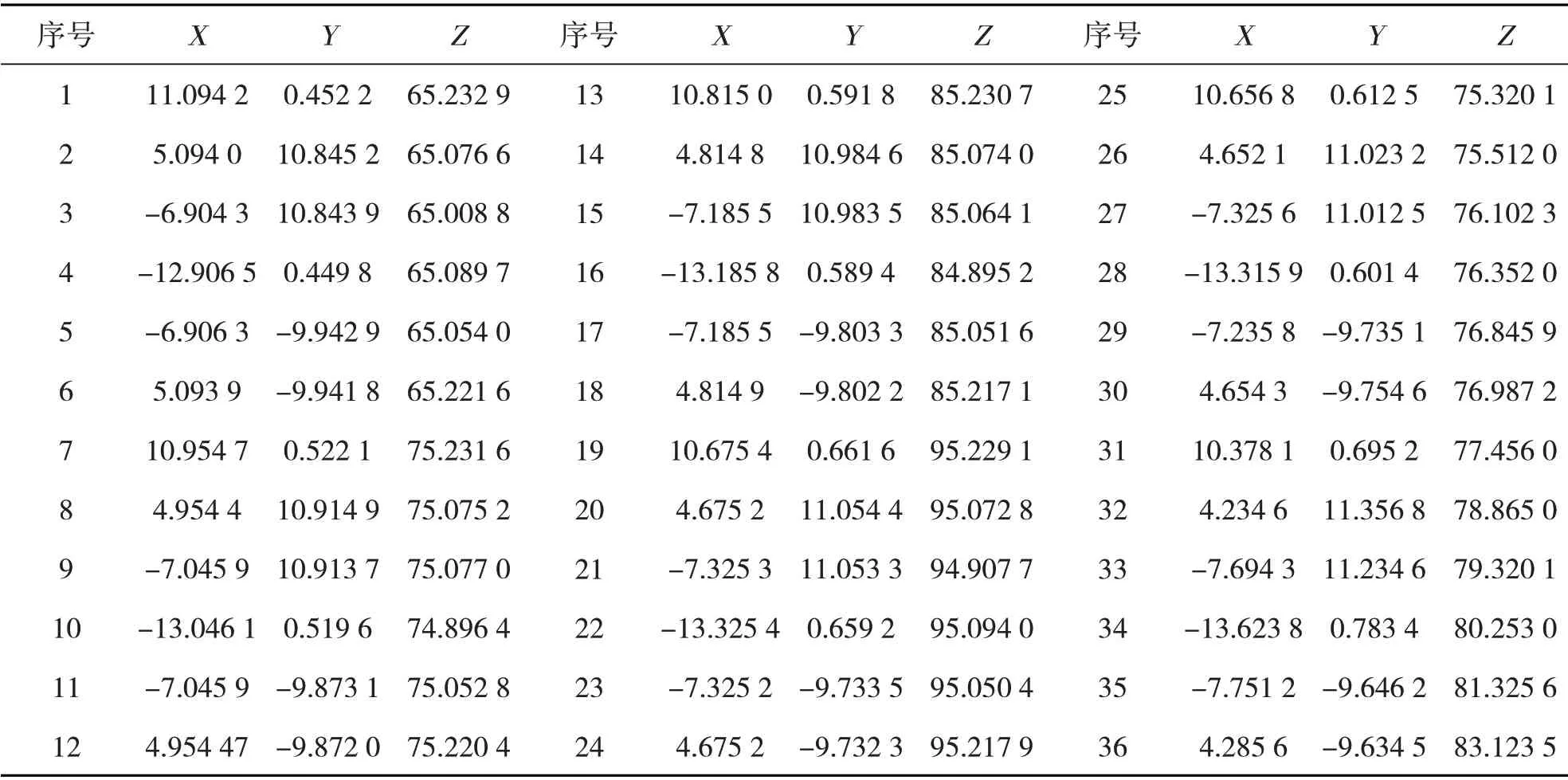
表1 三坐标测量机的采样数据 mm
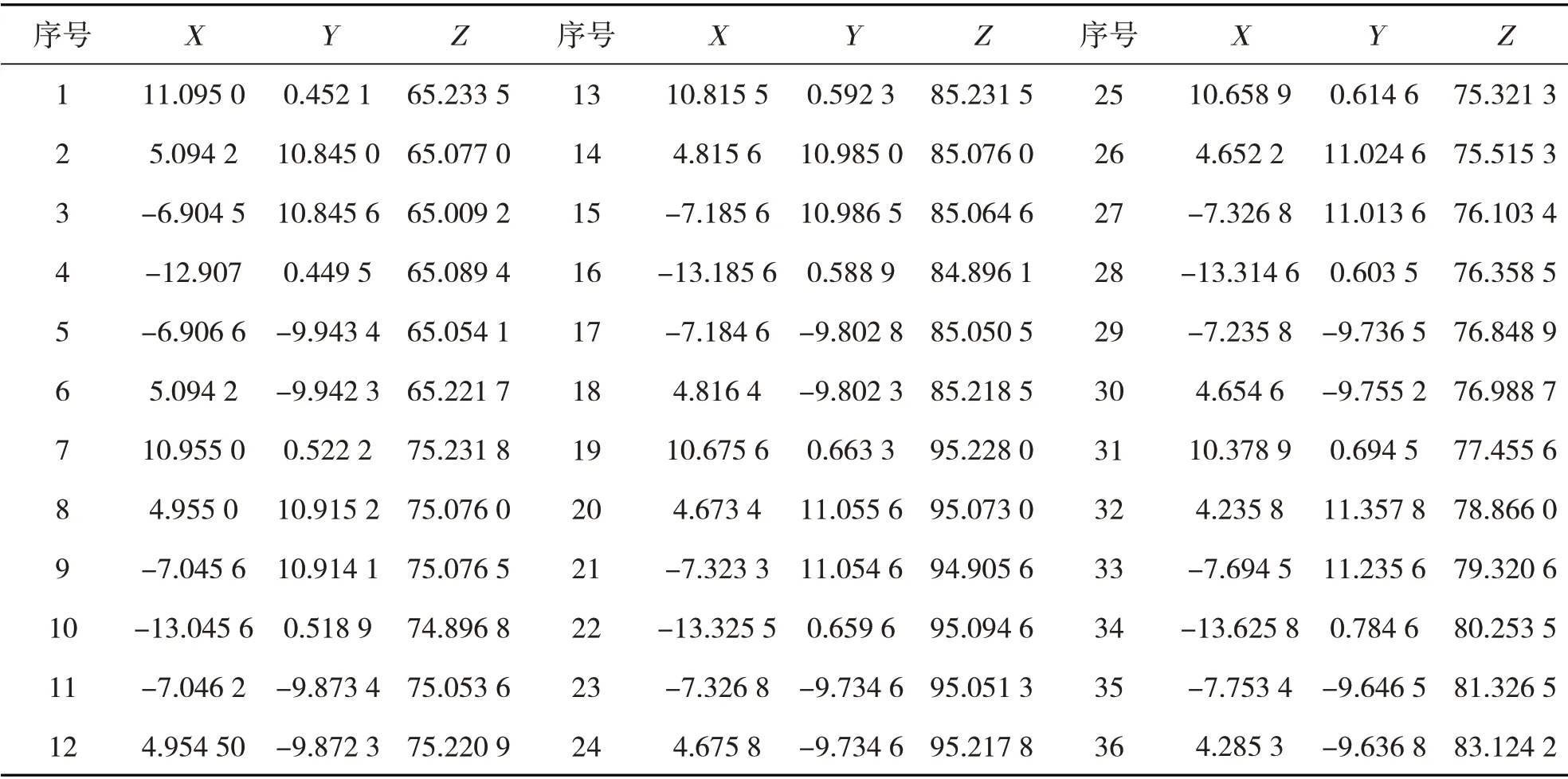
表2 激光三角法测量的采样数据 mm
3.2 数据误差评定
3.2.1 Matlab优化工具箱介绍
在进行数据误差评定前先要选取算法。优化工具箱是Matlab 数值计算扩展计算能力的函数工具[10],包括了常用的一些优化算法模型。表3 和表4列出了几种常见的函数及其求解类型。

表3 极小值问题函数

表4 极小值问题函数列表
在求解过程中,通常会根据目标函数是否具有可微性来选择算法。表3 中要求目标函数具有可微性的算法有fminbnd、fmincon、fminimax 和fmi‐nunc,而ga 和fminsearch 不要求目标函数可微。在表4 中,lsqlin 和lsqnonneg 可用于线性最小二乘问题;lsqcurvefit 和lsqnonlin 可用于非线性最小二乘求解。根据圆柱度误差的目标函数不可微并且不是凸函数,选取ga遗产算法。
3.2.2 误差评定
在ga 遗传算法中,初值对遗传算法的最终结果具有很大的影响。因此,其求解过程如下:
1)确定最小二乘初值,代入(Xi,Yi,Zi),用lsqnon‐lin算法求解,得到最小二乘解(a*,b*,p*,q*,R*)。
2)坐标转换,如将(Xi,Yi,Zi)转变为(xi,yi,zi)。
3)依据前面算法的设计,利用Matlab程序对圆柱度误差进行评定。将表1和表2中的坐标数据代入目标函数中,分别利用激光测量系统和三坐标测量机获得采样数据,用最小二乘法和最小区域法对其圆柱度误差进行评定,通过fminsearch 算法求解,将激光测量系统的评定结果与三坐标测量的结果进行比较,结果如表5 所示。同时,绘制圆柱度误差评定结果的数据曲线,如图5 所示。结合表5与图5 可知,激光三角法的测量结果具有很好的可靠性,可以用于在线检测环境。
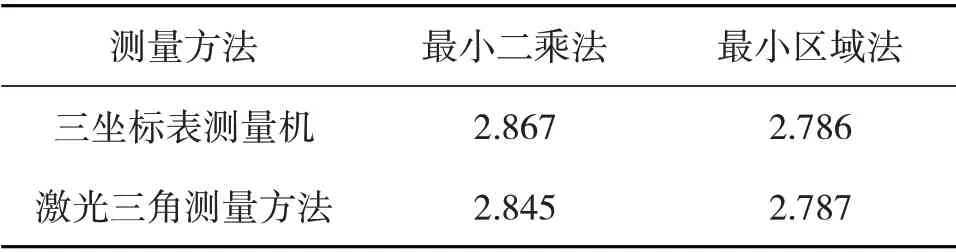
表5 圆柱度误差评定结果

图5 圆柱度误差评定结果曲线
4 结论
1)激光三角法测量数据的最小区域法评定结果与三坐标测量机的结果几乎相同,说明线性误差很小。
2)两次最小区域法的误差评定结果都小于最小二乘法的误差评定结果,说明最小区域法的误差评定方法在符合最小条件原理的同时,还能够有效地收敛到全局最优点。
3)当激光三角法测量评定方法用于实际测量时,评定时间较短,速率较快,具有一定的优势。通过误差评定结果可知,在圆柱度误差评定的测量方法中,基于激光三角法的测量方法是可行的。
——目镜套筒

