地下仓小麦粮堆热湿传递试验研究
王振清,张祥祥,陈 曦
(河南工业大学土木工程学院,河南 郑州 450001)
我国是人口大国,同时也是农业大国,保障粮食安全是重中之重的大事,储粮安全不仅是实现粮食食品安全的重要保障之一,更关乎国计民生[1-2]。大量实践和研究表明,低温环境不仅能抑制粮内酶活性、延缓粮食劣变,更能抑制病虫害的发生[3]。现阶段,我国储备粮库多为平房仓、浅圆仓、立筒仓等仓型,而地下仓依托其天然低温环境能够较好地保护粮食品质和减少药物熏蒸而备受关注[4-5]。储粮实践表明,温度和湿度是安全储粮的两个主要因素,因粮堆结露而引起局部霉变、发热是安全储粮的重大威胁之一[3]。因此,对粮堆温湿度的分布研究具有重要意义。
国内外学者对不同仓型内粮堆温度场和湿度场进行了大量的研究。Thorpe等[6-7]采用数值模拟的方法建立了粮堆内部温湿度耦合的数学模型,通过模型能够较好地反映出粮堆内部温湿度场分布特点。Beukema等[8]对矩形粮仓中自然对流过程进行了研究,发现粮堆内部温度的分布受自然对流的影响,自然对流过程提高了传热率,最终使得粮堆内温度场的分布处于一个稳定状态,本研究对数学模型中考虑自然对流和不考虑自然对流进行了对比分析,经过计算得出两者温度差值达11%。Jia等[9]在二维笛卡尔坐标系中建立了圆筒仓内粮堆的温度场模型。戚禹康等[10]基于计算流体力学理论,对稻谷自然储藏过程中热湿耦合传递进行了研究,探究了外部环境温度的变化对自然储藏过程中粮堆温度变化和粮食颗粒内部的热湿迁移过程的影响。亓伟等[11]在考虑粮食颗粒自呼吸的情况下,以局部热湿耦合传递过程为研究对象,对粮堆内部热湿耦合传递进行了研究,分析了非人工干预条件下粮仓在自然对流作用下粮堆内部温度场分布和水分迁移规律。尉尧方等[12]基于多孔介质理论和传热传质理论,对密闭储藏粮堆自然对流和热湿传递进行了分析,得出在自然对流条件下,低速的水分迁移对储粮过程中温度变化的影响较小,且自然对流过程对粮堆内部温度趋于均匀起到促进作用。王小萌等[13]对玉米粮堆霉变发热过程中的温湿度场变化规律进行了研究,通过试验揭示了玉米粮堆中温度场和湿度场的变化规律,并用粮库浅圆仓进行了验证,结论为进一步定量分析储粮过程中粮堆内部温湿度的扩散提供支持。刘文磊等[14]利用自制粮堆试验装置,就储粮压力对粮堆温度场的影响以及热湿传递的影响进行了研究,并借助多物理场数值模拟软件,对不同工况进行了数值模拟,最后用模拟结果验证了试验结果。王振清等[15-16]和金立兵等[17]对地下仓储粮期间温度场变化进行了数值模拟分析,得出仓内粮堆温度随着储粮时间变化的规律,并通过试验验证了模拟的准确性。
国内外学者对平房仓、浅圆仓和立筒仓内粮堆温湿度变化进行了大量研究,对地下仓温度场的研究虽有所涉及,但目前仍相对较少。本试验通过对模型仓内温湿度的监测,分析了仓内粮堆温湿度动态变化规律,并与数值模拟结果进行了对比,验证了模型的可靠性,进而为不同条件下粮堆温湿度场模拟打下基础,同时为制定相关措施提供依据。
1 材料与方法
1.1 试验装置
试验装置由模型仓、数据采集系统两部分组成。模型仓采用聚丙烯塑料加工而成,仓壁厚度为10 mm,仓身直径为500 mm,仓体高度为700 mm,为更好地模拟地下仓形状,仓底采用锥型设计,仓体的锥斗高度为140 mm,锥斗与水平面夹角为35°;模拟仓装粮后,上部留有高度为150 mm的空气域,空气域上部采用聚氨酯保温隔热板进行封闭,保温隔热板厚度为80 mm。
数据采集系统包含TOPRIE-TP700多路数据记录仪和TOPRIE-TP2305温湿度传感器。温度测试范围为-40~125℃,温度测试精度为±0.3%,湿度测试范围为0~95%(未结露),测量精度为±3%。
1.2 测点布置
在模型仓内布置测点以记录仓内温湿度变化,在大气环境中布置1个测点以记录环境温湿度的实时变化。本次测试共布置4层,共18个测点,从上到下测点间距依次为150 mm、200 mm、200 mm;从左到右测点间距依次为150 mm、200 mm、150 mm。从上到下依次为第1层~第4层。具体布置图及仓型图见图1。
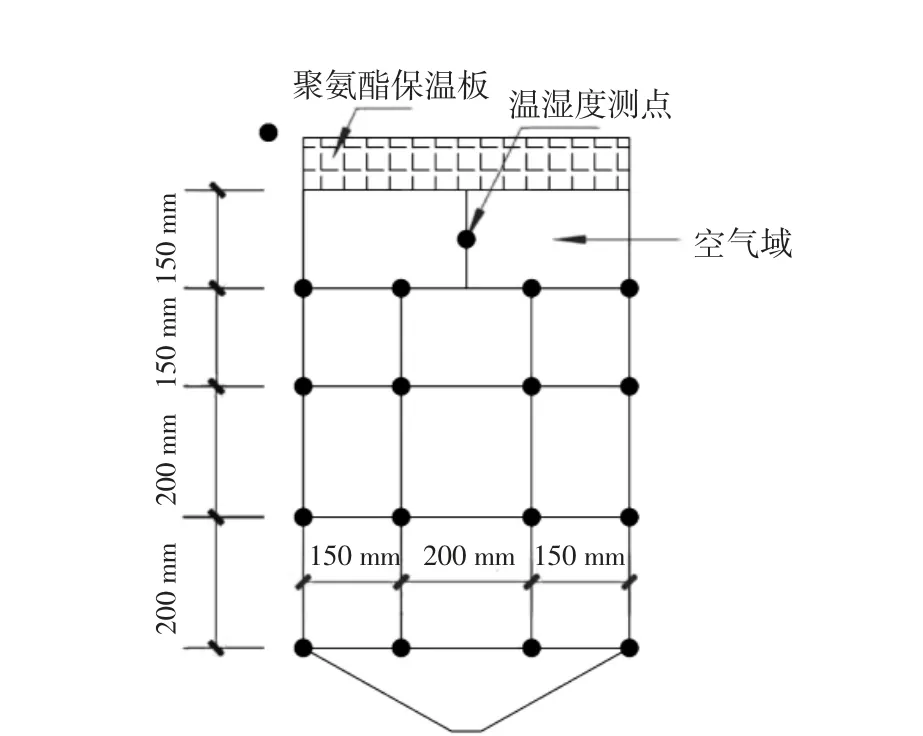
图1 仓型和测点布置图Fig.1 Warehouse type and measuringpoint layout
1.3 试验材料参数
在粮食行业中,仓容的计算以小麦容重为准,故本次试验材料选用小麦。为保持仓顶的绝热状态,仓顶盖采用聚氨酯保温隔热板进行封闭,具体参数见表1。
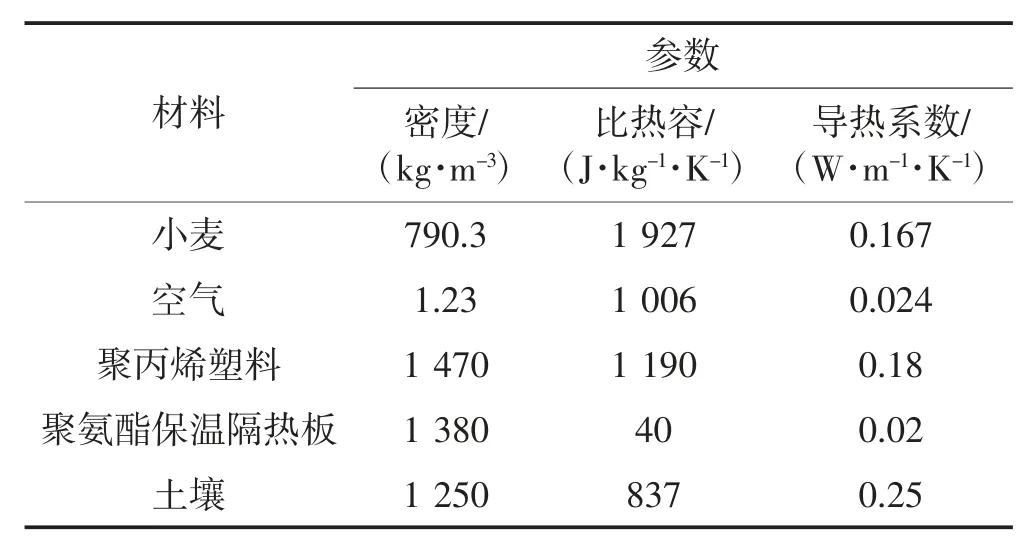
表1 材料参数表Table 1 Material parameter table
1.4 数据处理
本次试验共对模型仓进行了96 h的温湿度监测,每次的记录时间间隔为30 min。利用Origin对数据进行处理,每6 h显示一个数据点。
2 结果与分析
2.1 环境温湿度变化对仓内空气域温湿度的影响
如图2和图3所示,仓内空气域温度随环境温度的波动变化而变化,但波动幅度较小,为3.8℃,且温度的波动具有一定的滞后性,滞后近4 h,主要是由于土壤温度会在一定程度上受到环境温度变化的影响,且聚氨酯保温隔热板虽然导热系数很小(λ=0.02 W/(m·K)),但并非绝热,仍会有热量通过热传导的方式进入模型仓内与空气发生热交换,导致仓内空气域温度波动形式与外部环境温度波动形式相同。相比于温度,仓内空气域的相对湿度不受环境相对湿度变化的影响,外部环境相对湿度的波动较大,但并未能带动仓内空气域相对湿度的变化,这是由于模型仓仓体采用的材料为聚丙烯塑料,且顶部用聚氨酯保温隔热板密封,外部环境的湿空气很难渗透进模型仓内。
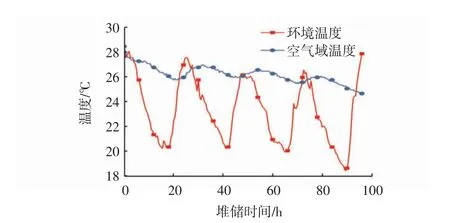
图2 环境温度对仓内空气域温度的影响Fig.2 Influence of ambient temperatureon air temperature in the warehouse
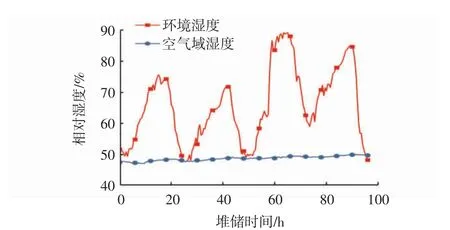
图3 环境相对湿度对仓内空气域相对湿度的影响Fig.3 Influence of ambient relative humidity on air temperature in the warehouse
2.2 粮堆各层温湿度
为比较模型仓温湿度在粮堆中不同高度的分布特点,对各层温湿度数据取平均值进行分析,其变化规律如图4、5所示。
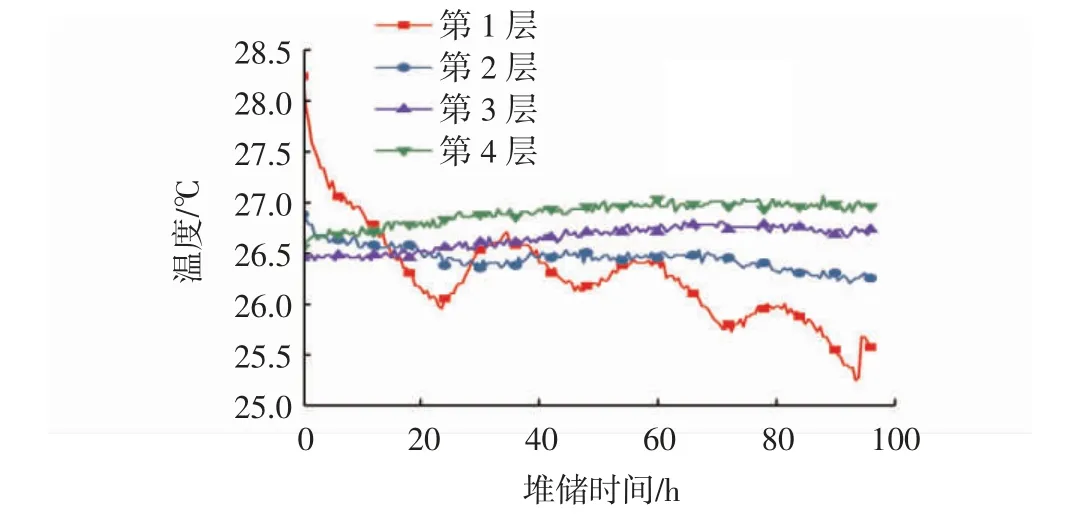
图4 仓内各层温度变化趋势Fig.4 The trend of temperature alteration in each layer of the warehouse
由图4可知,由于第1层温湿度测点位于粮食装粮线处,仓内空气域温度的变化直接影响第1层温度的变化,该层温度变化较其他层波动大,且呈现逐渐降低趋势,测试时间段内,降幅达2.7℃。第2、3、4层整体温度波动幅度较小,由于环境温度呈现逐渐降低趋势,环境这一波动趋势致使仓内空气域出现同样波动变化趋势,但在仓内粮堆中,随着粮食深度的增加,空气域温度的变化对粮层温度的影响越来越小,这是由于粮食是一种不良导体(λ=0.167 W/(m·K)),热量传递较慢;测试期间,第2、3、4层内温度变化幅度分别为0.6℃、0.8℃和0.4℃。由此可知,地下仓温度变化特点为:气温影响地温,地温影响仓内空气域温度,仓内空气域温度再逐步影响到粮堆各层温度,仓内整体粮温较稳定,其受外部环境的影响较小。
由图5可知,对比分析全部4层相对湿度的变化,第1层粮食由于接近仓内空气域,受空气域湿空气的影响,其相对湿度接近于空气域相对湿度,故与其他3层相对湿度差别较大,第1层相对湿度随着空气域相对湿度的增加呈现逐渐上升趋势,而第2、3、4层呈现逐渐下降的趋势,这是由于浮升力的存在使得湿空气上升,导致表层相对湿度增加。
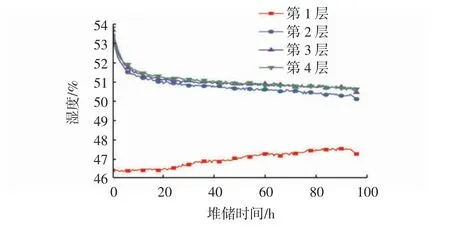
图5 仓内各层相对湿度变化趋势Fig.5 The trend of relative humidity alteration in each layer of the warehouse
2.3 粮堆横向温湿度变化
对距离仓壁不同距离的粮堆温湿度变化进行分析,由于温湿度测点关于中线对称布置,故把贴近壁面的测点与粮堆中测定各自求平均值后进行比较分析,其变化趋势如图6、7所示。
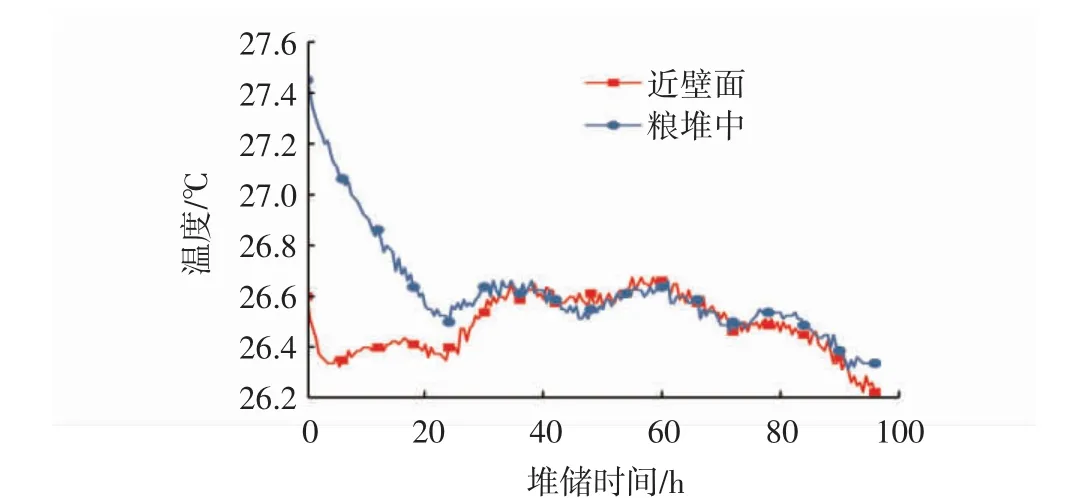
图6 近壁面处和粮堆中温度变化规律Fig.6 The temperaturealteration patternsnear the wall and inside the grain pile
由图6可知,粮堆中温度呈现逐渐下降趋势,降幅为1.1℃,这是由于仓外土壤温度低于仓内粮堆温度,模型仓外冷量渗透进粮堆导致的;近壁面温度随着时间的推移,虽有波动,但整体上呈下降的趋势,降幅为0.4℃,这是由于近壁面温度受到外部土壤温度和内部粮堆温度的双重作用所导致的。
由图7可知,近壁面相对湿度和粮堆中相对湿度整体上均呈现逐渐降低的趋势,与相对湿度在纵向变化机理相同,均是受到湿浮升力作用,湿空气从粮堆中逐渐逸散到空气域中,导致粮堆中相对湿度逐渐降低。
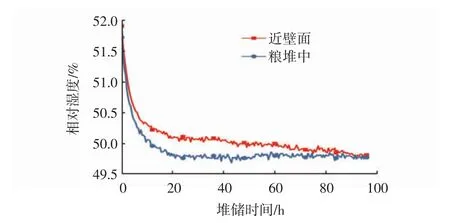
图7 近壁面处和粮堆中相对湿度变化规律Fig.7 Relativehumidity alteration patternsnear thewall and inside the grain pile
3 数值模拟
3.1 数学模型的建立
粮堆是一种典型的多孔介质,地下仓储粮在非人工干预条件下,其影响因素包括仓体外土壤环境、大气环境等。在储粮过程中,仓内介质会因温度差的存在发生热交换,为简化计算,假定粮堆均匀分布,且忽略粮堆的自呼吸和粮食颗粒间的辐射作用,将地下仓储粮过程中的传热过程视为非稳态传热过程,其对应的方程如下。
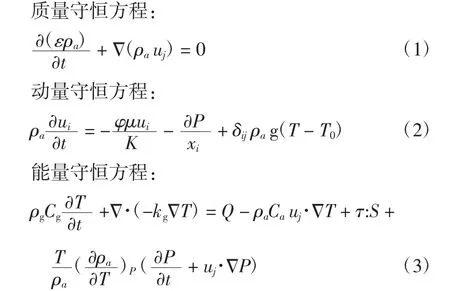
忽略压力功、黏性发热和由于粮食颗粒自呼吸产生的热量,则能量守恒方程简化为:
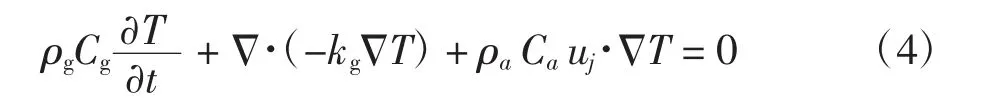
式中:ε为孔隙率;ρa为空气密度,kg/m3;uj(j=1,2)为xj方向空气的流动速度,m/s;u1=u,u2=v;μ为动力黏度系数,N·s/m2;K为渗透率,m2;g为重力加速度,m/s2;T为热力学温度,K;ρg为粮食密度,kg/m3;Cg为粮食比热容,J/(kg·K);kg为粮食导热系数,W/(m·K)。
3.2 物理模型的建立
利用多物理场数值模拟软件COMSOL对模型仓进行数值模拟。为了减少土壤温度对模型仓的影响,建立物理模型时,使土壤面积远远大于仓体面积,且假定土壤区域初始温度相同。受太阳高度角的影响,到达地表的太阳辐射通量密度随时间变化趋势呈类似正弦波的变化规律[18]。因此,土壤的热通量在上下传输过程中也会呈现出相应的波动,其变化规律可用具有正弦函数位相滞后和温度变幅衰减的方程表示,土壤温波方程为:

3.3 模拟结果
本研究对模型仓进行了96 h数值模拟分析。由温度场云图(图8)可知,外部环境温度降低时,冷量先渗透至土壤,再从土壤通过仓壁进入模型仓内,故表现出仓内靠近仓壁面处的温度首先降低。云图则为波浪分层形式,这符合冬季储粮表现出的“冷皮热芯”变化趋势。
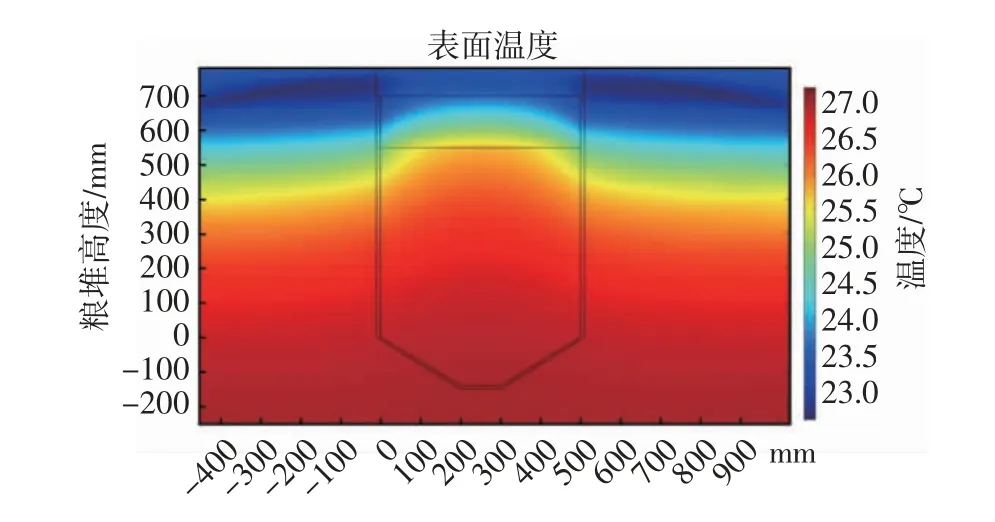
图8 仓内温度场云图Fig.8 Cloud map of temperaturefield in the warehouse
3.4 模拟与实测对比
以粮堆第3层为例,对数值模拟温度变化和实测温度变化进行对比分析,结果如图9所示。
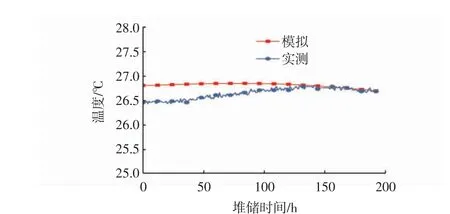
图9 数值模拟与实测温度对比Fig.9 Comparison of numerical simulation and measured temperature
由图9可知,实测值和模拟值变化趋势相同,且逐渐趋于一致。实测值和模拟值初始值不同是由于实测误差造成的,误差为1.3%,在允许范围内。随着时间的推移,伴随着粮食颗粒与空隙间湿空气热湿交换的进行,实测值和模拟值的偏差逐渐减小并趋于一致。通过数值模拟和实仓测试数据的对比分析,验证了数值模拟所用模型的可靠性,后续可以通过改变数值模拟的边界条件和相应的变量进行多因素下粮仓的预测。
4 结论与建议
本文通过对模型仓温湿度的测试,并结合土壤温波方程作为插值函数,在多物理场数值模拟软件中建立了以聚丙烯塑料为材料的地下仓物理模型,并且对模型进行了与实仓测试相同时间的数值模拟分析,经过模型仓实仓数据与数值模拟数据的对比分析,得出以下结论:
(1)模型仓内空气域温度随环境变化而变化,波动幅度最大为3.8℃,且表现出滞后性,滞后时长达4 h;环境相对湿度的变化未对仓内空气域的相对湿度造成影响。
(2)粮堆表层温湿度受仓内空气域温湿度影响,环境温度的变化通过对仓内空气域的影响进而影响粮堆表层温度,随着纵向深度的增加,仓内空气域温度对粮层温度影响越来越小。
(3)粮堆中温度和仓壁面处粮堆温度均随着时间的延长逐渐降低,相对湿度由于受湿浮升力影响也随着时间的延长逐渐降低。
(4)通过模型仓实测数据和数值模拟数据的对比,验证了本文所建立的数值模拟模型的准确性和可靠性。
本文对模型仓实测数据有限,数值模拟中所建立模型的准确性仍需更多的实测数据去验证。地下仓储粮过程中温湿度变化是多种因素共同作用的结果,对地下仓温湿度变化还需要更深入的研究。

