一种弹道外测数据的野值处理方法
李坤坤,曹 锐,胡亚雄
(西北核技术研究院,西安 710024)
0 引言
在测控设备跟踪弹道目标试验中,外测数据作为目标态势感知和设备跟踪性能考核的重要依据,在数据分析工作中具有重要的作用。然而,由于复杂作战环境干扰、相关设备的系统故障,或设备人员的判断失误和操作失准等原因,测量信息不可避免地会出现一部分偏离被测信息趋势特征的异常点,这些异常点便称为野值[1]。野值的存在将直接影响到数据的处理精度与分析结果,因此,有必要在外测数据预处理过程中,对它们进行检测识别与剔除修正。
通常情况下,野值根据是否连续可划为孤立野值和斑点野值两种类型,孤立型野值是指数据序列中非持续出现的某一独立时刻异常跳变点;斑点型野值是指数据序列中持续出现的幅度较为接近的成片异常跳变点[2]。当前围绕孤立型野值处理常见的有差分检测法及多项式外推拟合法[3-4],其剔除作用显著,但对斑点型野值的处理不太理想,易导致野值识别不完全、剔除效果有限及部分有用信息连带被删除等缺陷。围绕斑点型野值的处理常见有Kalman 滤波、稳健滤波M 估计、最小二乘B 样条逼近等方法[5-7],这些方法能较好地识别并剔除连续野值点,但剔除效果不稳定、剔除后出现数据缺失,以及处理方法较复杂造成使用受限等问题依然存在。此外,传统野值剔除方法(如White 准则、Grubbs 准则及Romanovsky 准则)对数据对象的统计特性有特定要求[8],且存在一些符合时变趋势的正常数据超出准则所用判断门限,因此,直接采用这些准则可能会删除部分有用信息。
在综合考虑上述方法优缺点基础上,本文设计一种基于最小二乘趋势项建模与一阶差分还原的肖维涅准则联合处理方法,可以较好地剔除弹道外测数据中的复杂类型野值,并保证原始数据的稳定性。
1 最小二乘法趋势项建模
最小二乘法(Least Square,LS)是法国数学家A.M.Legendre、Gauss 等人提出的一种数理统计学分析法,在各领域试验及统计数学中得到了大量应用。针对一些具有低阶多项式的简单类型趋势项,或高阶多项式的复杂类型趋势项的实验数据,可利用最小二乘多项式拟合对数据趋势特征完成优化建模[9],其建模步骤为:
1)对一组实验数据,根据其趋势特征设定一拟合多项式,并基于LS 原理建立矩阵方程;
2)解方程得多项式系数矩阵,从而得符合数据趋势项的最小二乘拟合曲线。


2 肖维涅准则

值得说明的是,对于判别式(6)中的肖维涅准则系数k,其取值一般与测量数据长度N 有关,可通过查系数表选取。本文采用文献[11]给出的系数高端拟合公式,即

3 野值剔除流程
由弹道导弹动力学可知,飞行弹道轨迹具有一

如图1 所示,对影响数据处理性能的测量野值δn,预处理剔野值的具体流程为:
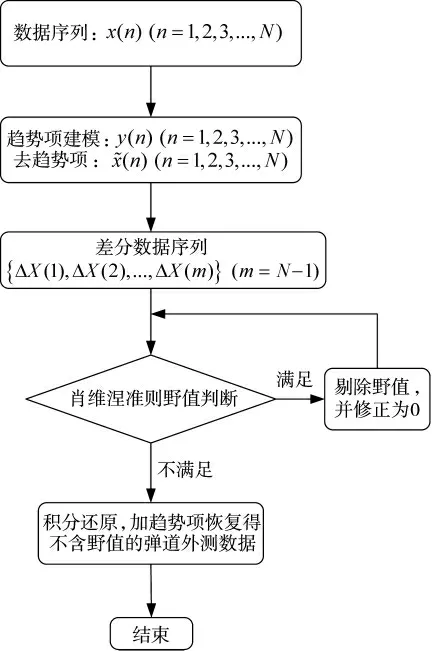
图1 联合方法剔野值流程图

4 仿真分析
为检验本文联合野值剔除方法,在MATLAB 平台使用二次多项式仿真弹道位置数据,如式(11)所示。仿真时间64 s,数据率20 Hz,叠加45 dB 信噪比的高斯随机噪声,并人为添加一部分两种类型野值,如图2 所示。

图2 弹道外测仿真数据
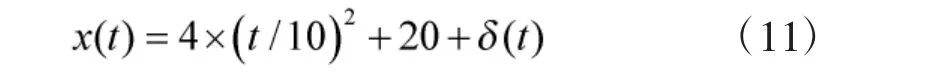
利用本文设计的联合剔除野值法展开处理,先根据最小二乘原理对数据趋势项建模。由图3 可见,所建立的趋势项较好地拟合了弹道位置数据的时变规律,剔除趋势项后的数据如下页图4 所示。对去趋势项数据作一阶差分,由图5 可见,斑点型野值全部转变为孤立型野值,从而使野值类型得以简化,便于后续进一步处理。利用本文联合方法中带高端拟合系数的肖维涅准则(肖维涅系数按高端拟合公式取为3.549),对差分处理后的数据进行野值剔除,剔除后的效果如图6 所示,可以看出,在该检验准则循环作用下孤立野值全部得以剔除。

图3 弹道趋势项

图4 去趋势项后外测数据

图5 一阶差分处理后数据

图6 肖维涅准则剔除结果
为更好地比较本文联合方法与其他方法的剔野效果,根据文献[8]中表2 对各测量数据事后野值预处理方法的分析总结,考虑到本文算例采样数据量大、野值类型较为复杂的特点,选用同样可化斑点野值为孤立野值的奇偶提取方法[12]作为对比。为保证对比条件的一致性,两种方法均采用最小二乘法进行趋势项建模,并采用相同迭代检验次数下的肖维涅准则进行野值剔除。所不同的是,本文方法采用一阶差分处理完成野值简化,而文献[12]的奇偶提取法,是通过多次数据抽取分组将斑点野值拆分为不同组别下的孤立野值。
在一致性条件对比下,图7 给出了本文方法与文献[12]奇偶提取法的对比效果图,其中后者奇偶提取次数取为2。可以看出,本文方法对图6 去野值数据积分并叠加趋势项后,便可得到用于后续弹道分析的位置外测数据,且不损失有用信息;而文献[12]奇偶抽取法,在一致性条件下仍存在部分野值不能识别与剔除的问题。这是因为在外测数据斑点野值较多、范围较广时,相比本文方法一阶差分步骤一步即可简化斑点野值的方便快速性,有限次数的奇偶抽取并不能使该部分野值达到较好的孤立稀疏度,而增加抽取次数又必然增加分组趋势建模的工作量(m 次抽取次数得2m组数据,对应2m组数据趋势项建模)。因此,本文联合方法不仅可以对复杂类型野值取得较好的处理效果,还可满足靶场试验外测数据事后快速分析的需求,说明了本文方法的实用性。

图7 两种方法剔野效果对比
5 结论
野值的存在对弹道外测数据的应用具有不可忽视的影响,对此本文提出一种基于最小二乘趋势项拟合与一阶差分的联合处理方法。仿真结果表明该方法不仅简便易行,还可抑制复杂类型野值的不利影响,取得较好的处理效果。下一步将针对在极端不利的测量环境下,采集数据信噪比急剧减小时,积分步骤容易积累长程误差情况下的复杂类型野值处理作出改进工作。

